例谈理想化模型的构建与教学应用

方润根 叶晟波

(1. 杭州学军中学,浙江 杭州 310012；2. 浙江省慈溪中学，浙江 慈溪 315300)

物理核心素养导向下的教学,要求学生能运用科学思维方法来解决问题,如建模、比较、概况、抽象等．[1]模型作为一种重要的科学方法,具有解释科学现象、作出科学预见、形成科学发现、启发科学思维等功能．[2]其中,理想化模型作为模型的重要表现之一,有助于学生将复杂问题简单化,突出问题的主干,把握研究对象的本质,其构建过程与应用过程在高中物理教学中备受关注．为此,物理课堂教学应该为学生创设真实问题情境,引导学生剖析问题、简化过程,形成物理概念,建立理想化模型,运用正确的方法解决问题,并进一步做到物理概念的迁移．在此以高中物理必修1中物理实在的质点与物理必修2中非真实存在的电场线为例,阐释理想化模型的构建与教学应用．

1 真实物理问题情境的创设及向物理问题的转化

高中物理课程标准指出,[1]创设情境进行教学,对培养学生的物理学科核心素养具有关键作用．在物理教学中,应让学生应用物理观念思考问题、应用物理知识分析解决问题,把问题中的实际情境转化成解决问题的物理情境,建立相应的物理模型．

真实问题情境是从真实世界中捕获的真实问题和这一问题的情境脉络,它存在或产生于我们的日常生活实践之中,具有真实性、情境性、结构不良性、互动性等特点．[3]真实情境可以源于学生与科学相关的生活事件与经验,有助于发散性地提出问题;也可以源于差异性实验,引发学生的认知冲突,产生疑问;[4]还可以源于社会热点或科技发展前沿,有利于学生感受知识推动科技发展．[5]“质点”是生活中常见运动分析中的重要概念,可以以学生生活熟悉的场景作为情境,引导提炼可探究的物理问题．

情境1： 以雄鹰在空中翱翔的视频作为真实场景,视频分为近景和远景,近景展示了雄鹰拍打翅膀,展翅飞翔的模样,学生能清晰地看到雄鹰翅膀的扇动,意识到雄鹰有一定的大小和形状;远景是从地面上的人的视角看到天上有一个黑点在移动．同样的雄鹰展翅,引导学生针对不同场景可探究问题的提出与研究对象的明确．针对该真实情境,可以提出的问题如下.

问题1:近景中,雄鹰是怎样运动的?

问题2:地面上的人们看到的雄鹰是怎样运动的?

问题3:为什么可以用一个点来代表“雄鹰”,研究它的运动呢?

问题1是近景视角,问题2是远景视角,通过近景的呈现,学生会认为雄鹰有大小和形状,在运动时身体各部分的运动情况不一样;但通过远景的呈现,学生发现从地面上看只能观察到一个“黑点”的运动．通过两者的对比,认识到在描述雄鹰整体的运动情况时,可以将它视为一个点．进而回答问题3,思考能将“雄鹰”视为点的条件:当翅膀的运动方式和雄鹰形状对所研究的问题来说是可以忽略的次要因素时,可以将雄鹰简化为一个黑点．

情境2： 以学生生活中常见的系列场景为真实情境,如高速公路行车、游乐场娱乐项目、花样游泳比赛、火车通过长江大桥等系列的真实场景．引导学生从系列的真实场景中提炼研究问题、明确研究对象,判断能否将高速路上奔驰的汽车、乘坐刺激过山车的游客、花样游泳比赛过程中的运动员、通过大桥的火车等就是“质点”?定义或抽象为质点是否需要条件?在什么研究问题与研究对象中可视为“质点”?

2 物理概念的形成或前概念转变

奥苏贝尔认为概念形成是指学习者从大量同类事物的不同实例中归纳出共同的本质特征,要经过知觉辨别、假设、检验假设和概括4个阶段．[6]例如学习“质点”这一概念时,学生首先基于真实情境,感知生活中可以被视为质点的物体,如研究翱翔的雄鹰、行驶的汽车、过山车上的游客的运动轨迹时,能将雄鹰、汽车和游客视为质点;在此基础上,形成关于质点的初步印象:在描述物体的运动时,可以将运动的物体视为质点;此后检验这一假设,发现不是所有“运动的物体”都能被视作质点,同样的真实场景,有时不能视为质点,如研究花样游泳运动员的姿势、火车通过大桥的时间时,运动员和火车都不能看作质点;再进一步精确假设:当物体的形状和大小对研究问题影响很小时,可以把物体看作质点．通过反复证明后,就获得了质点的基本特征．在概念形成的过程中,要不断寻找正例与反例,借助正例来肯定本质特征,借助反例来排除非本质特征．

在新、旧概念冲突的情况下,需满足一定条件学习者才能转变已有概念．波斯纳等人认为,概念转变有4个条件：[7](1) 对现有概念的不满．只有当某一概念失去作用时,学习者才可能改变现有概念．当学习者面对现有概念无法解释的事实,从而引发认知冲突,能有效导致对现有概念的不满．(2) 新概念的可理解性．学习者应理解新概念的真正含义,这需要它建立整体一致的表征．(3) 新概念的合理性．学习者需要看到新概念是合理的,为此新概念需要与学习者所接受的其他概念,学习者的理论、经验、直觉等保持一致．(4) 新概念的有效性．学习者应看到新概念的价值,它能解决其他途径难以解决的难题,向学习者展示新的可能与方向．

以“电场线”的教学为例,学生容易理解点电荷的电场线,但在理解等量同种点电荷和等量异种点电荷的电场线时可能会产生“两个电荷之间的电场线会相交”这一迷思概念．由于学生在绘制等量同种正电荷的电场线时,会基于点电荷的经验单独绘制两个正电荷的电场线,这时两个正电荷之间的电场线便存在交叉,一个点对应两个电场强度方向．但学生在电场强度的学习中已经知道电场中某一点的电场强度只有一个方向,由此会产生一定的认知冲突．教师引导学生对两个正电荷间某一点所受的电场强度进行具体分析,可以选择等量同种正电荷连线上的中点．根据学生绘制的图像,连线中点处有相反的两个方向,无法判断电场强度真实的方向．提醒学生最初判断电场强度的方法,连线中点处的试探电荷会受到两个大小相等方向相反的静电力,根据力的合成得到合外力为0,电场强度也为0．进而引导学生从电场强度的叠加这一角度来理解电场线不会相交．接着,教师还应提出新问题,要求学生判断等量异种电荷之间某点处的电场线方向,以此检验学生的掌握情况．

3 建构理想化模型——本质与条件

不管“质点”、“电场线”概念的形成还是基于原有迷思概念的转变,只是对物理知识(概念)的理解．“质点”、“电场线”等区别于某些具体的概念,还需要通过“理想化”过程,引导学生理解“‘质点’、‘电场线’是理想化模型”的过程,阐释“理想化”的过程中,理解“质点”、“电场线”作为“理想模型”这一方法的本质与条件．

3.1 物理过程“理想化”到“质点”理想化模型的构建

物理过程的理想化是因为生活中的运动过程是比较复杂的,为了研究问题的方便,可以忽略次要因素,突出物体运动的本质特征和属性,把运动过程抽象为一种简单的、实际上不存在但又经得起实践验证的运动过程．以某省高考选考试题为例.

例1.如图1所示,一企鹅在倾角为37°的斜冰面上,先以加速度α=0.5 m/s2从冰面底部由静止开始沿直线向上“奔跑”,t=8 s时,突然卧倒以肚皮贴着冰面向前滑行,最后退滑到出发点,完成一次游戏)．若企鹅肚皮与冰面间的动摩擦因数μ=0.25,已知sin37°=0.6,cos37°=0.8．求:

图1 企鹅的运动

(1) 企鹅向上“奔跑”的位移大小;

(2) 企鹅在冰面上滑动的加速度大小;

(3) 企鹅退滑到出发点时的速度大小．

分析： 该题中的研究对象是企鹅,描述其运动时,不需要关心企鹅翅膀和头部的运动方式,只关注它从哪里移动到了哪里,不必在意它的形状,所以可以看成一个质点来描述它的运动．在研究企鹅完成一次游戏的过程中,有两个实际情境:

情境1： 有一企鹅在倾角为37°的斜冰面上,从冰面底部由静止开始沿直线向上“奔跑”．过程中企鹅受到重力、支持力、静摩擦力和空气阻力4个力,静摩擦力作为企鹅奔跑的动力．

情境2：企鹅突然卧倒以肚皮贴着冰面向前滑行,最后退滑到出发点．企鹅受到重力、支持力、滑动摩擦力和空气阻力4个力．学生分析发现实际情况空气阻力随速度变化,是个变力,企鹅不是做严格的匀变速直线运动．

但是,企鹅游戏过程中速度不大,忽略空气阻力影响,按照匀变速运动去处理产生的偏差很小,对研究问题的影响很小,而且计算简单,所以只保留过程的主要因素,把游戏过程转化为物理过程,再把物理过程“理想化”,建立物理运动模型．

企鹅的游戏这一实际过程的“理想化”过程: (1) 初速为0的匀加速直线运动,(2) 匀减速直线运动．在对物体运动的理想化过程的研究中,很容易发现实际过程中所包含的规律,能更准确更深刻的抓住问题的实质．

3.2 “电场线”理想化模型的构建——研究对象“理想化”

对象模型是根据研究对象的特点,抓住主要、本质因素,将物质自身形态理想化,从而建立起能够反映研究对象主要特征的模型．[8]下面以建构点电荷、等量异种电荷和平行板的电场线模型为例,通过实践获取并加工信息,识得3种带电体电场线的基本特征,从而引导学生抽象概括、建构“电场线”这一理想模型．

“电场线”这一理想模型的理解中,需要引导学生经历对“点”、“多个点”、“线或面”到“体”研究对象的变化分析过程．针对“点”电荷(以“正电荷”为例),如何描述该点电荷的电场强度的大小、方向,周围多个位置的场强方向．学生需要以“电场线”形象、方便地描述电场的方向,即电场线上每一点的切线方向都与该点的场强方向一致(引导学生画出该正电荷周围多个位置的场强方向),观察电场线离正电荷越近呈现越密的分布(如图2),引导学生发现电场线的分布可以形象描述电场强度大小．

图2 正点电荷的“电场线”

针对“多个点”(如等量异种电荷),是在点电荷基础上,结合叠加原理,绘制等量异种电荷周围某位置的场强,多个位置的场强分布(如图3)．如何实现研究对象从“点”、“多点”到“面”(如“平行板”)的电场线“理想化”过程?基于“点”、“多点”模型,引导学生认识到如何将“面”这一研究对象转化为多个“点”,即将一块无限大的均匀带正电的金属板视为无数均匀分布的正电荷[如图4(a)]．金属板上各点对板外某点P的电场强度是对称的,可依据叠加原理得到P点处的电场强度方向[如图4(b)],依次绘制可得到带正电的金属板外各位置的电场强度方向[如图4(c)],根据对称思想,绘制带正电的金属板上方的电场线,得到带正电的金属板的电场线分布[如图4(d)],同理可得带负电的金属板的电场线分布[如图4(e)]．此时,将两块带等量异种电荷的金属板正对放置,依据叠加原理,得到平行金属板面方向的电场为0[如图4(f)]．这时,就建立起平行金属板的电场线理想化模型,即电场方向垂直板面,电场线的疏密程度相同,板间的电场(除边缘附近)可看作匀强电场[如图4(g)]．

图3 等量异种电荷的“电场线”

(a)

4 解构理想化模型——物理概念的应用与迁移

理想问题是从大量实际问题中抽象出来的,是为了便于概念理解与“理想化”模型的建构,但单“建构”是不够的,还需通过将理想化模型应用于真实更为复杂的场景中的应用与迁移,解构理想化模型中形成科学思维与物理观念．正如有学者所说,教师提供的问题情境应扩展学习者所接触的应用范围,促使学习者建构出灵活可用的知识,[9]解构理想化模型的过程,是教师引导学生理解“真实场景问题”是在什么条件下视为“理想问题”,以数学的、图像的、文字的表征及转化实现理想化模型这一物理概念的应用与迁移．

在质点的教学中,雄鹰、企鹅的运动更贴近学生的生活实际,学生在掌握质点概念后,教师可以进一步创设微观情境和宏观情境,加深学生对质点概念的理解,需要由宏观场景中的概念理解与理想化模型的建构,拓展到微观、宇观场景中的应用．如研究核外电子绕原子核的运动时是否可将原子看作质点?研究带电粒子在电磁场中的运动时又是否可将带电粒子看作质点?在分析研究对象中进一步理解带电粒子在电磁场中的受力情况与运动过程．又如研究地球自转运动时可否将地球看作质点?在比较火星与地球绕太阳公转运动时又可否将火星与地球都看作质点?“质点”理想化模型的应用,有助于进一步分火星与地球绕太阳运动的轨道周长、线速度、角速度、向心加速度等．

在“电场线”理想模型的教学中,关于“电场线”模型的应用场景的拓展,也是需要基于学生对点电荷、等量异种电荷和平行板电场中的电场线分布的理解与综合应用,才能在更为复杂的真实场景中解决问题．

例2.如图5所示,电量为+q和-q的点电荷分别位于正方体的顶点, 正方体范围内电场强度为0的点有

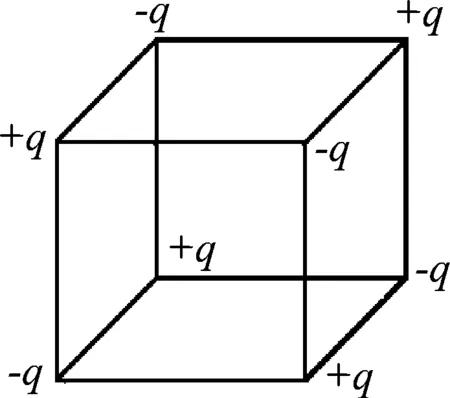
图5

(A) 体中心、各面中心和各边中点.

(B) 体中心和各边中点.

(C) 各面中心和各边中点.

(D) 体中心和各面中心.

该问题是考查正方体顶点的点电荷在空间某点场强的分布, 突破了一条直线或一个平面内的求和模式,[10]学生根据等量同种电荷在其连线的中点处的合场强为0的特征,不难分析出各面中心的电场强度为0;在体中心,可以分析上下底面对角线所在平面,得体中心的合场强也为0;在各边中心,根据等量异种电荷在连线上的中点场强不为0的特点,排除各边中点电场强度为0的选项,由此选(D)．

总之,理想化模型的教学是一个逐步的过程,需要教师在教学中创设情境,引导学生提炼物理问题,在问题的探究过程中达到概念的形成或转变,并进一步学习模型方法.通过不断改变情境,让学生在解决实际问题的过程中实现模型的建构与应用,提升学生分析迁移能力,对理想化模型的认识达到升华．