基于逻辑回归-信息量的川藏交通廊道滑坡易发性评价
杜国梁 ,杨志华 ,袁 颖 ,任三绍 ,任 涛
(1.河北地质大学城市地质与工程学院,河北 石家庄 050031;2.河北省高校生态环境地质应用技术研发中心,河北 石家庄 050031;3.中国地质科学院地质力学研究所,北京 100081;4.中国地质科学院水文地质环境地质研究所,河北 石家庄 050061)
川藏交通廊道位于青藏高原中东部地区,包括从成都通往拉萨的G317、G318和在建川藏铁路沿线区域(图1),是世界上构造活动最强烈和地貌演化最迅速的地区之一。伴随着青藏高原的隆升,内、外动力地质作用强烈交织与转化,塑造了复杂特殊的地质环境条件和强烈的河谷动力学过程,导致区内滑坡灾害极其发育[1-3]。频繁发生的滑坡灾害不仅造成重大的人员伤亡和财产损失,而且严重影响着川藏铁路的建设与安全运营,制约着区域经济的发展[4-5]。然而,受高寒、高海拔、交通条件差的制约,研究区滑坡调查受到一定限制。整合已有调查数据、分析研究区滑坡分布规律、预测区内滑坡空间分布特征具有十分重要的意义。

图1 研究区地质背景图Fig.1 Geological background map of the study area
滑坡易发性评价是在现有滑坡调查、编目的基础上,分析评价斜坡体在所处的地层岩性、地形地貌、地质构造、气象水文等因素组合下发生失稳、破坏的可能性[6]。滑坡易发性评价常用的方法有确定性和非确定性方法,其中确定性方法主要为基于斜坡稳定性的定量计算,非确定性方法主要包括层次分析法、模糊综合评判、信息量法、概率比、逻辑回归、神经网络、支持向量机等数学分析方法,这些方法在区域滑坡易发性评价中都取得了良好的应用效果[7-13]。其中,信息量法由于其物理意义明确、操作简单、实用性强,在地质灾害评价领域得到了广泛应用。但是,信息量法属于“暗箱”操作,它只反映评价因子不同类别在组合情况下对灾害发生的影响,并没有考虑各评价因子之间的相关性,以及各因子对灾害发生影响的差异[14]。逻辑回归模型作为应用最为广泛的回归模型之一,可以很好地拟合各评价因素的非线性特征,且各因子不需要符合正态分布。充分发挥逻辑回归和信息量2种评价模型的优势,建立逻辑回归-信息量组合模型,对于提高预测精度具有十分重要的意义[15]。
本文在资料收集整理、遥感解译和野外地质调查的基础上,选取岩性、坡度、坡向、坡形、地形起伏度、地形粗糙度、断裂密度、河流距离等8个影响因子,采用逻辑回归-信息量评价模型,评价川藏交通廊道的滑坡易发性,并分析、检验评价结果。本研究可为区内公路、铁路、水电工程的规划建设和防灾减灾提供参考。
1 地质背景
川藏交通廊道地势西高东低、地形起伏度大,从海拔500多米的四川盆地跃升到4 000多米的青藏高原,横跨横断山脉、念青唐古拉山、冈底斯山、喜马拉雅山等山脉,穿越岷江、大渡河、雅砻江、金沙江、澜沧江、怒江、雅鲁藏布江等多条大江大河。受第四纪以来青藏高原快速隆升的影响,研究区大江、大河在高原地区河谷深切,常形成高山峡谷地貌。
川藏交通廊道从东向西穿越扬子地块、川滇块体、甘青块体、西藏块体和喜马拉雅块体,地层岩性复杂,从第四系至震旦系均有分布,岩性以砂岩、板岩、泥岩、灰岩、白云岩、页岩、片岩、千枚岩、花岗岩、闪长岩、片麻岩、玄武岩及第四系松散沉积物为主。
伴随欧亚板块碰撞、挤压,青藏高原快速隆升,在区内形成了龙门山断裂带、鲜水河断裂带、金沙江断裂带、澜沧江断裂带、怒江断裂带、嘉黎—察隅断裂带、雅鲁藏布江断裂带等多条区域性大型活动断裂带。活动断裂在历史上曾多次发生强震,如1933年发生Ms 7.5叠溪地震,1950年发生Ms 8.6察隅地震、1973年发生Ms 7.9炉霍地震、2008年发生Ms 8.0汶川地震等,这些大地震均诱发了大量的地震滑坡灾害。
2 评价方法
信息量模型最早由Shannon提出,殷坤龙等[16]首次将其应用到地质灾害评估领域。信息量模型中,第i个影响因子分级指标对滑坡发生事件提供的信息量(Ii)表示为:

式中:Si—分布在第i个影响因子分级中已发生滑坡的个数;
Ai—第i个影响因子分级所占的面积;
S—评估区滑坡总个数;
A—评估区总面积。
逻辑回归(logistic回归)是一种广义的线性回归分析模型。在逻辑回归模型中,P为滑坡发生的概率,通过Logit变换,对滑坡发生的概率P和不发生的概率1-P的比取自然对数,即ln(P/1-P),建立线性回归方程:

式中:x1,x2,···,xn—滑坡影响因子;
β0—常数项;
β1,β2,···,βn—回归系数。
充分发挥逻辑回归模型和信息量模型的优势,建立逻辑回归-信息量组合模型,建立的主要步骤为[17]:①用式(1)计算影响因子分级指标提供的信息量;②用式(4)对信息量值进行归一化;③以归一化信息量值为自变量,滑坡发生为1,不发生为0,作为因变量,用式(5)进行回归计算,得到各影响因子的回归系数;④将式(5)中计算得到的z值带入式(2),计算得到滑坡易发性指数值P。
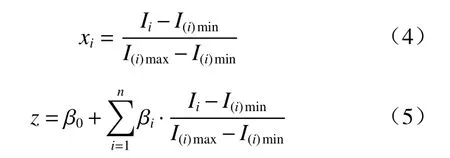
式中:xi—第i个影响因子分级指标提供的信息量归一化值;
Ii—第i个影响因子分级指标提供的信息量;
I(i)min—第i个影响因子分级指标所属影响因子分级指标类中提供的信息量最小值;
I(i)max—第i个影响因子分级指标所属影响因子分级指标类中提供的信息量最大值。
3 滑坡影响因子分析与检验
3.1 数据来源
本研究使用的数据包括:(1)历史滑坡数据:主要来自1∶5万和1∶10万县市地质灾害详细调查资料,以及野外实际的补充调查资料;(2)数值高程模型(DEM):来源于地理空间数据云,ASTER GDEM V2版,空间分辨率为30 m×30 m。坡度、坡向、地形起伏、坡形和地表粗糙度提取于DEM;(3)岩性和断裂数据:来源于1∶50万地质图;(4)主要河流和行政区划数据:来源于研究区1∶100万地理底图。
3.2 影响因子分析
(1)岩性
岩性是滑坡灾害的物质基础,影响斜坡受侵蚀的难易程度和滑坡发育类型。将地层岩性按软硬程度划分为:Ⅰ坚硬的层状和块状岩的砂岩、板岩、灰岩、白云岩、玄武岩、花岗岩等;Ⅱ较坚硬-坚硬的层状的砾岩、板岩、砂岩、泥岩;Ⅲ软硬相间的砂泥岩、泥岩夹灰岩、白云岩夹泥岩、千枚岩等;Ⅳ软弱-较坚硬的片岩、页岩、千枚岩、泥砾岩及火成岩;Ⅴ软质的散体结构5个等级(图2)。由表1可知,研究区软硬相间的砂泥岩、泥岩夹灰岩、白云岩夹泥岩、千枚岩等岩组的信息量值最大,最有利于滑坡的发生。

图2 研究区岩性分布图Fig.2 Lithology map of the study area
(2)坡度
坡度与滑坡发生的关系十分密切,是滑坡形成的主控因素之一。坡度影响斜坡内的应力分布、斜坡上松散固体物质的厚度、植被覆盖度、地表水径流,从而影响斜坡的稳定性。将坡度划分为:0~10°、10°~20°、20°~30°、30°~40°、40°~50°、>50°共6个等级(图3);研究区在30°~40°范围内,最有利于滑坡的发生,其次为20°~30°,在<10°的范围最不利于滑坡的发生(表1)。
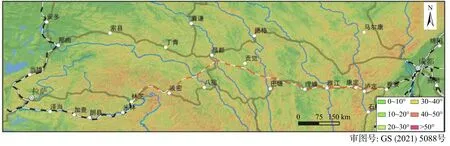
图3 研究区坡度分级图Fig.3 Slope gradient map of the study area

表1 信息量统计表Table 1 Information value of landslide contributing factors
(3)坡向
不同坡向太阳辐射强度不同,影响斜坡的植被覆盖、水分蒸发和风化程度,进而影响斜坡的稳定性。将坡向划分为:-1°(平面)、337.5°~22.5°(北)、22.5°~67.5°(东北)、67.5°~112.5°(东)、112.5°~157.5°(东南)、157.5°~202.5°(南)、202.5°~247.5°(西 南)、247.5°~292.5°(西)、292.5°~337.5°(西北)9个等级(图4);从表1可以看出,研究区面向南、东南方向的斜坡滑坡容易发生,面向北的斜坡最不利于滑坡的发生,平面无信息量值,无滑坡发生。

图4 研究区坡向分布图Fig.4 Slope aspect map of the study area
(4)地形起伏度
地形起伏度是一定范围内最高点和最低点海拔的差值,可以反映地表的起伏变化,与滑坡分布存在一定的相关性。本文将地形起伏度划分为:<50 m、50~100 m、100~150 m、150~200 m、200~250 m、>250 m共6个等级(图5)。由表1可以看出,地形起伏度在150~200 m时,滑坡发生的可能性最大,100~150 m次之,<50 m最不利于滑坡的发生。

图5 研究区地形起伏度分布图Fig.5 Topographic relief map of the study area
(5)坡形
坡形可以影响坡体内地下水的分布,凹形坡在斜坡表面更易集水,在地震载荷作用下凸形坡的地震放大效应等,这些都影响坡体的稳定状态。将坡型划分为:凹形坡、平直坡和凸形坡(图6)。从表1可以看出,在研究区滑坡发生的可能性:凸形坡>凹形坡>平直坡。

图6 研究区斜坡坡形分布图Fig.6 Slope shape map of the study area
(6)地表粗糙度
地表粗糙度是反映地表起伏变化和侵蚀程度的指标,从一定程度上反映了构造运动伏度,对地质灾害的发生具有重要的意义。很多学者将地表粗糙度作为滑坡影响因素用于滑坡易发性评价[18]。本文将地表粗糙度划分为<1.1、1.1~1.2、1.2~1.3、1.3~1.4、1.4~1.5、>1.5共6个等级(图7)。由表1可以得到,研究区地表粗糙度在1.4~1.5信息量最大,最有利于滑坡的发生,1.3~1.4次之,1.1~1.2滑坡发生的可能性最小。

图7 研究区地表粗糙度分布图Fig.7 Surface roughness map of the study area
(7)断裂密度
断裂密度体现了一个区域遭受构造作用改造的强度和构造的复杂程度,也反映了区域地表的破碎程度,与滑坡发育存在一定的相关性[14]。本文将断裂密度划分为:0~5 m/km2、5~10 m/km2、10~15 m/km2、15~20 m/km2、20~25 m/km2、>25 m/km2共6个等级(图8)。由表1可以看出,随着断裂密度的增大,研究区滑坡发生的可能性增大。

图8 研究区断裂密度分布图Fig.8 Fault density map of the study area
(8)河流距离
河流对斜坡体坡脚的冲刷和淘蚀加速了斜坡体的变形破坏,从而导致滑坡的发生。河流距离与滑坡分布具有很好的相关性。本文将河流距离划分为:0~200 m、200~400 m、400~600 m、600~800 m、800~1 000 m、>1 000 m共6个等级(图9)。由信息量统计表(表1)可以看出,随着与河流距离的增加,滑坡发生的可能性基本呈减小的趋势。

图9 研究区河流距离分布图Fig.9 Map showing distance to rivers of the study area
3.3 因子多重共线性检验
进行Logistic回归时,各自变量需要保证相互独立,若因子相关性高,会出现多重共线性。采用容忍度(Tolerance,TOL)和方差膨胀因子(Variance Inflation Factor,VIF)对自变量进行多重共线性诊断:

其中,R2是以xi为因变量时对其他自变量回归的复测定系数。TOL为VIF的倒数,当TOL大于0.1且VIF小于10时,说明自变量不存在多重共线性。
采用SPSS进行多重共线性检验,检验结果见表2,结果显示所选8个因子的TOL均大于0.1且VIF均小于10,表明各因子相互独立,不存在多重共线性。
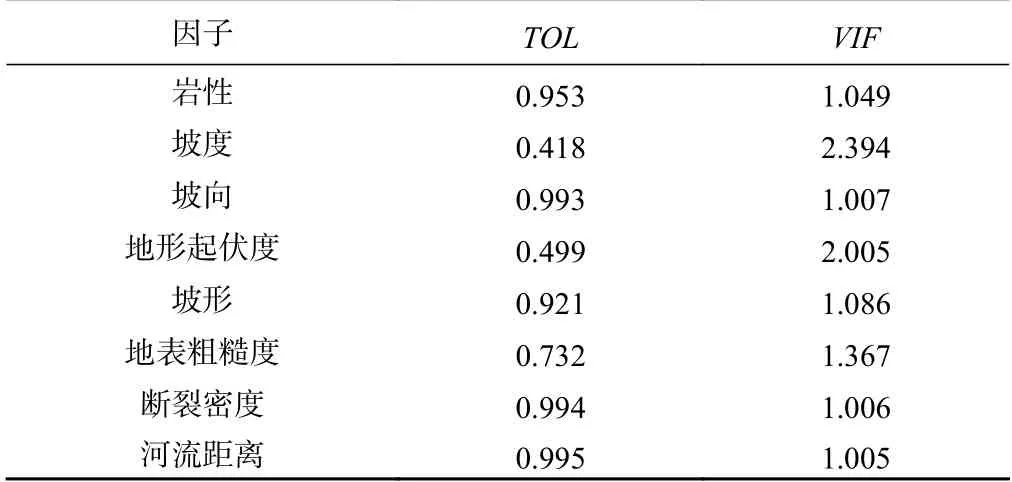
表2 评价因子共线性诊断Table 2 Multi-collinearity analysis of contributing factors
4 易发性评价
4.1 评价结果
在逻辑回归-信息量模型中,滑坡发生的因变量值为1,不发生的因变量值为0。随机生成结合遥感解译判别、修正,生成与滑坡点数相同的非滑坡点4 820处。基于GIS提取各点的各影响因素的归一化信息量值,并在SPSS中进行回归分析,得到各因子的回归系数(表3)。

表3 模型相关参数Table 3 Relevant parameters of the model
将各因子回归系数带入式(5),得到:

式中:Il—岩性;
Is—坡度;
Ia—坡向;
It—地形起伏度;
Iq—坡形;
Ir—地表粗糙度;
If—断裂密度;
Iri—河流距离。
在GIS中,将z值代入式(2)得到滑坡易发性指数值P。根据易发性指数将研究区划分为高易发(0.8~1)、中易发(0.6~0.8)、低易发(0.6~0.4)和极低易发(<0.4)4个易发区(图10)。

图10 川藏交通廊道滑坡易发性评价图Fig.10 Landslide susceptibility map of the study area
4.2 评价结果检验
(1)显著性检验
回归分析需要检验自变量对因变量影响的显著性。采用Wald统计量对应的Sig.值判断因子的显著性,若因子的Sig.值小于0.05表明影响因素对滑坡的发生有显著的影响[17]。由表3可知岩性、坡度、坡向、地形起伏度、坡形、地表粗糙度、断裂密度、河流距离等8个因子的显著性Sig.均小于0.05,通过检验。
(2)精度验证
ROC曲线(receiver operating characteristic curve)即感受性曲线,曲线下方面积(AUC)可以评价模型预测结果的准确度。一般认为:AUC值小于等于0.5时,模型预测失败,AUC值为0.5~0.7时,预测准确性较低,AUC值为0.7~0.9时,预测准确性较高,AUC值在0.9以上,说明预测准确性极高。采用ROC曲线对逻辑回归-信息量模型评价结果的准确性进行检验,得到ROC曲线下的面积为0.81(图11),说明模型评价结果在研究区具有较高的准确性,能够很好地预测研究区滑坡的发生。

图11 逻辑回归-信息量模型的ROC曲线Fig.11 ROC curve of the model
4.3 评价结果分析
从易发性评价结果可以看出(表4和图10),研究区滑坡高易发区面积83 464.69 km2,占研究区总面积的13.00%,主要分布在坡度陡峭、地形起伏度大的大渡河、雅砻江、金沙江、澜沧江、怒江、雅鲁藏布江、易贡藏布江等的大型河流深切河谷的两岸,以及龙门山断裂带、金沙江断裂带、澜沧江断裂带、怒江断裂带、边坝—洛隆断裂带等活动断裂控制区,区内地表切割强烈,岩体破碎;中易发区面积204 267.96 km2,占研究区总面积的31.79%,主要分布在坡度较为陡峭、地形起伏度中等的大江、大河及深切河谷支流两岸;低易发区面积166 022.27 km2,占研究区总面积的25.84%,主要分布在坡度相对较缓,断裂密度较小的大型河流支流的两岸;极低易发区面积188 728.76 km2,占研究区总面积的29.37%,主要分布在坡度平缓、地形起伏小、断裂不发育的地区。通过统计不同易发区的滑坡、非滑坡数量和密度,可以看出随着易发程度的增强,滑坡点密度不断增大,而非滑坡点的密度不断减小,说明易发分区是合理的(表4)。
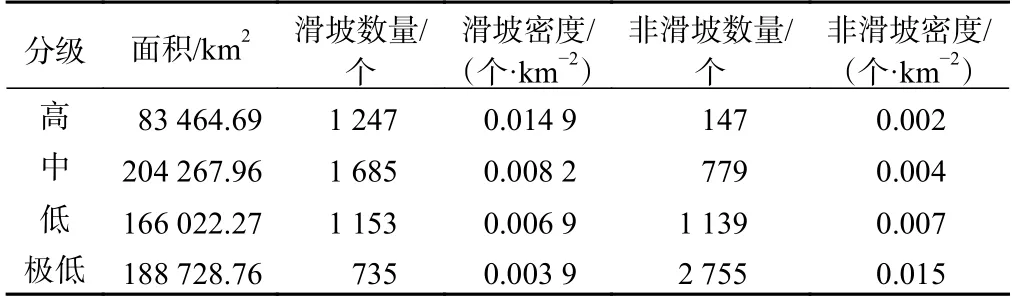
表4 不同易发区滑坡统计结果Table 4 Relevant parameters of the model
研究区在工程规划和建设时,应尽量避开滑坡高易发区,必须穿越高易发区时,应对该区段斜坡进行详细勘查,对滑坡隐患点采取相应的工程治理措施。在高、中易发区,需尽量避免工程建设和运营时对地质环境的扰动,以免诱发滑坡灾害,同时,应加强滑坡隐患的排查工作。在低易发区,仍需对潜在发生的地质灾害进行风险防范,并做好应急保障工作。
5 结论
(1)结合逻辑回归和信息量模型的优势,采用逻辑回归-信息量方法对研究区滑坡进行易发性评价。共收集整理川藏交通廊道滑坡4 820处,同时,通过随机生成结合遥感解译调整,生成同等数量的非滑坡点用于易发性评价。
(2)选取岩性、坡度、坡向、坡形、地形起伏度、地形粗糙度、断裂密度和河流距离8个因素作为评价因子,通过因子共线性和显著性检验,得到所选8个因子不存在多重共线性,且均对滑坡发生影响显著。通过ROC曲线对模型预测结果进行检验,评价结果的准确率达81%,表明评价结果能够很好地预测研究区滑坡的发生。
(3)研究区高易发区主要分布龙门山断裂带、怒江断裂带、金沙江断裂带、澜沧江断裂带、边坝—洛隆断裂等活动断裂带控制区,以及大渡河、雅砻江、金沙江、澜沧江、怒江、雅鲁藏布江、易贡藏布江等大型河流深切河谷的两岸。中易发区主要集中在岸坡较陡、地形起伏度中等的大型河流支流的两岸。在工程规划、建设和运营阶段,需加强上述区域滑坡隐患的排查和防治工作。

