基于深度堆叠式稀疏回归的癫痫患者脑电信号特征选择*

张远鹏，蔡可夫，姚 敏，姚登福，王 理

（1 南通大学医学院医学信息学系，南通 226019；2 香港理工大学医疗科技与资讯学系；南通大学附属医院3 神经内科，4 临床医学研究中心；南通大学5 信息科学技术学院，6 智能信息技术研究中心；7 南通先进通信技术研究院有限公司)

脑电图（electroencephalogram，EEG)作为生物标志物在脑机接口（brain-computer interface，BCI)中发挥重要作用[1-2]。在临床诊断中经常使用EEG 来确定癫痫的存在和类型。近年来，随着人工智能技术的飞速发展，人工智能辅助诊断越来越受到人们的关注，且在许多场景中取得了空前的成功[3-4]。基于人工智能的癫痫患者辅助诊断流程包含信号采集、信号处理、特征提取、特征选择以及模型训练和测试。众所周知，从EEG 信号中提取的原始特征不能直接用于模型训练，因为它们通常在非常高维的特征空间中表示。因此，特征选择通常在模型训练之前执行。本研究探讨如何选择有效的特征以保证高效的人工智能辅助临床诊断癫痫。

1 资料与方法

1.1 一般资料 从波恩大学下载的癫痫EEG 数据将用于评估所提出的特征选择模型。该数据集由5组子集（A～E 组)组成，其中每组由100 个单通道持续时间为23.6 s 的EEG 段组成。A～B 组的片段取自5 例健康受试者，C～E 组片段取自癫痫患者。数据结构和收集条件见表1。每个组中1 个受试者的采集过程中的振幅见图1。

图1 每组一个受试者的振幅（从上到下分别对应A、B、C、D、E 组)

表1 健康受试者与癫痫患者EEG 数据集

1.2 方法 假设用X=[x1，x2，…xn]∈Rd×n表示癫痫患者EEG 训练样本集合，Y=[y1，y2，…yn]T∈Rn×c表示对应的标签集合，其中Xi=[x1，x2，…xn]T∈Rd样本特征空间，yi∈Rc表示xi对应的标签空间，1≤i≤n。对于矩阵B，使用bij表示第i 行和第j 列的元素bi，和bj分别表示矩阵的第i 行向量和第j 向量。F.P.NIE 等[5]基于l2，1-范数提出了一种嵌入式稀疏回归模型（E-JSRegression)，用于高维数据的特征选择，由于基于l2-范数的损失函数对离群点敏感，因此使用基于l2，1-范数的损失函数来消除离群点。此外，他们还使用l2，1-范数来正则化变换矩阵，从而可以进行特征选择。E-JS-Regression 目标函数定义为:

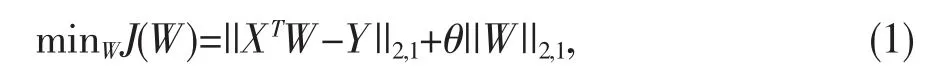
其中θ 是正则化参数，W∈Rd×c为变化矩阵。堆叠广义原理作为集成学习策略可以为模型组合提供有效的方法。尽管堆叠广义原理没有像Boosting 和Bagging 那样广泛使用，但是它的巨大创新已经在许多应用场景中取得了成功。本研究以E-JS-Regression 为基本单元，构建用于癫痫患者EEG 特征选择的深度堆叠式稀疏回归模型（SDE-JS-Regression)，见图2。

图2 SDE-JS-Regression 的栈式深度结构

SDE-JS-Regression 由m 个基本组件组成，这些基本组件以逐层方式连接。具体来说，当第一个组件固定时，后续组件的输入由两部分组成:原始输入特征和上一层组件的输出。本研究参照堆叠广义原理，随机生成投影矩阵，然后将随机投影矩阵集成到原始输入特征空间中，从而融合这两个部分。因此，可以通过以下等式获得第s 个组件（1＜s≤m)的输入，

其中Z∈Rc×d是随机投影矩阵，每个元素在[0，1]的范围内，σ 是一个正则化参数。利用这种结构，将原始输入特征添加到一个连续的随机投影中，从而将所有构件进行堆叠和桥接，形成本研究提出的特征选择模型。从堆叠深度结构中继承的优势在于:添加到原始特征中的随机投影可以堆叠的方式连续打开原始特征输入空间中存在的流形结构，使输入特征空间变得线性可分。

当通过SDE-JS-Regression 获得变换矩阵W∈Rd×c时，计算各列向量Wj的总和，然后对最终列向量中的元素从最大到最小排序。通过这种方式可以获得用于指导特征选择的特征等级列表。

1.3 实验设置 为了公平地评估SDE-JS-Regression 的特征选择性能，引入E-JS-Regression[5]、mRMR[6]、RFE-SVM[7]和Relief[8]用于基准测试。每种基准模型的简要概述为:（1)E-JS-Regression:这是一个嵌入式特征选择模型，也是本研究提出方法的基本组件。在实验中，其涉及的正则化参数γ 将由5 折交叉验证确定。（2)mRMR:这是一个基于最小冗余和最大相关性的过滤功能选择模型。冗余是通过相互信息来衡量的。（3)RFE-SVM:这是一个包装器特征选择模型，与支持向量机（support vector machine，SVM)分类器结合使用以实现递归特征消除。支持向量机中的参数全部由5 折交叉验证确定。（4)Relief:这也是一个过滤要素选择模型，它根据要素和类之间的相关性为每个要素分配权重。实验中最近邻居的数量设置为10。

当获得由每个模型生成的特征排序列表时，基于高斯核的SVM[9]和Ridge 回归[10]被用来执行分类任务。根据表2 中所示的癫痫脑电图数据，构造了3个分类任务。

表2 针对所选特征的3 个分类任务

对于每个任务，75%的样本用于训练，25%的样本用于测试。基于高斯内核的SVM 中的参数（内核宽度和松弛变量)和Ridge 中的正则化参数由训练集上的5 折交叉验证确定。实验重复测试程序100 次，并记录准确度的平均结果，其中准确度（Accuracy)定义为正确分类的样本数与所有样本数之比。

2 结果

2.1 所选特征的分类性能 图3～4 显示了从相应的特性排序列表中选择的具有不同特征数量（从5～100，步长为5)的5 个模型的分类性能，从3 个分类任务的比较结果中，观察到SDE-JS-Regression 的性能优于基准模型，尤其是mRMR、RFE-SVM 和Relief。在任务3 上，无论是SVM 或Ridge，当选择的特征数目设＞15 时，SDE-JS-Regression 总是比E-JSRegression 的准确度高。

图3 支持向量机分类性能

2.2 所选特征的参数分析 图5 显示了参数敏感性分析结果，其中包含正则化参数θ 和分量数m，其中θ 的搜素范围为[0.001、0.005、0.01、0.05、0.1、0.5、1、1.5、2、2.5]，m 的搜索范围为[1、2、3、4、5、6、7、8、9、10]。每个任务的准确性都是从特征排序列表中选择的前55 个特征获得。从图5 中，相对于θ，观察到SDE-JS-Regression 在[0.001，0.05]的范围内表现良好。随着θ 从0.05～2.5 的进一步增加，分类性能开始下降。但是，尽管当θ 在[0.05，2.5]范围内时性能开始下降，但是SDE-JS-Regression 的性能并未显示出明显的变化。

图4 岭回归分类性能

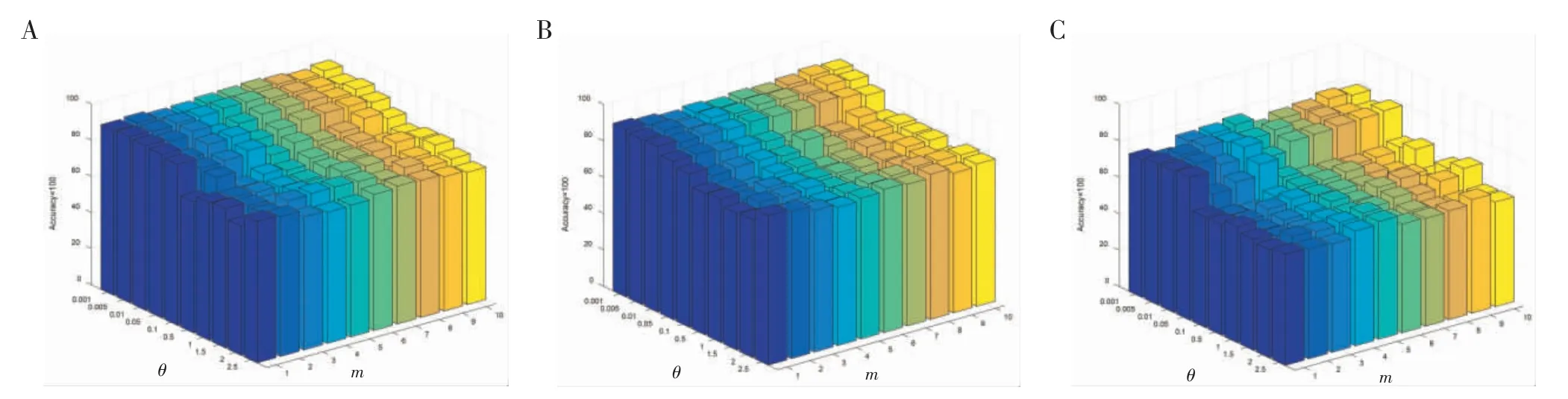
图5 关于θ 和m 参数敏感性分析

3 讨论

特征选择在EEG 处理中扮演着重要角色。目前大多数特征选择算法可以分为3 类:过滤式、嵌入式及包裹式。过滤式特征选择算法独立于分类器，主要是利用特征与对应输出之间的内在关系进行特征选择。具有代表性的特征选择算法包括mRMR、F-statistic[11]、Chi-square[12]、Relief 等。和过滤式不同，包裹式特征选择算法是将特征选择过程和分类器绑定，采用“尝试”的方式获得对分类器具有高区分度的特征。采用这类方式进行特征选择时，往往需要消耗大量的时间。具有代表性的方法包括CSF[13]、RFESVM 等。嵌入式特征选择和包裹式类似，也和分类器绑定。但是和包裹式不同的是将特征选择的过程纳入分类器的目标优化过程，而并非采用“尝试”的策略。这使得特征选择过程和分类过程浑然一体，具有代表性的算法包括E-JS-Regression 等。本研究在嵌入式特征选择算法E-JS-Regression 上，提出基于深度堆叠式稀疏回归模型SDE-JS-Regression 用于癫痫患者的EEG 特征选择。从实验结果中发现，与mRMR、Relief 和RFE-SVM 相比，嵌入式特征选择模型SDE-JS-Regression 和E-JS-Regression 获得的特征对分类器的归纳性更高。这是因为嵌入式特征选择模型在特征选择过程中将分类训练误差降至最低。因此，对于通过EEG 信号进行的癫痫分类任务而言，嵌入式特征选择模型更为合适。在3 个分类任务（尤其是任务3)上，SDE-JS-Regression 的性能优于E-JS-Regression，这表明所提出的堆叠式深度结构确实可以帮助选择更多的分类成瘾特征，从而提高分类性能。如前所述，从堆叠的深度结构中继承的好处在于，添加到原始特征中的随机投影可以帮助我们以堆叠的方式连续打开原始特征空间中存在的流形结构。有了这些好处，输入特征空间就变得线性可分。因此，提出的SDE-JS-Regression 对θ 具有一定鲁棒性。对于本研究的3 个EEG 分类任务，θ 可以设置为0.001～0.05。

SDE-JS-Regression 结构中的层（组件)数决定了添加到输入要素空间中的随机移位数。从图5 中可以看出，“层越多，性能越好”并不成立。在这3 个任务上，4～6 层可以保证相对较好的性能。太多的随机投影会导致训练集的分布失真。

本研究提出了一种特征选择模型SDE-JS-Regression，用于通过癫痫患者EEG 信号进行人工智能辅助临床诊断。SDE-JS-Regression 与现有的嵌入式模型有很大的不同，因为它的堆叠深度结构是基于堆叠广义原理以逐层方式构造的。SDE-JS-Regression 源自E-JS-Regression，但性能优于E-JS-Regression，因为添加到原始特征中的随机投影可以帮助以堆叠方式连续打开原始特征空间中存在的流形结构，这样原始输入特征空间就可以更线性地分离。基于所选功能构建3 个分类任务，以评估SDE-JSRegression 的有效性。

综上所述，通过SDE-JS-Regression 选择癫痫患者的EEG 信号特征更有意义，对分类器有所帮助，可比基准模型产生更好的性能。