稠油火烧油层高温氧化动力学参数计算与分析

张 弦，王海涛，车洪昌

(1.东北石油大学 石油工程学院，黑龙江 大庆 163318;2.大庆油田国际勘探开发公司，黑龙江 大庆 163000;3.中油国际(伊拉克)鲁迈拉公司，北京 100120)

0 引言

火烧油层是指向注入井注入空气，点燃油层后持续注入空气(或氧气)助燃，形成稳定的燃烧前缘，从而驱替大部分未燃烧的原油至生产井[1]。火烧油层过程伴随着复杂的传热、传质及物理化学变化。在前缘推进过程中，烟道气、水蒸汽、气相烃与凝析油混相，随着燃烧的持续，不断向生产井推进，形成复杂的驱替过程[2]。在火烧前缘的前方，原油经氧化或裂解生成的类焦物质沉积在岩石表面，并作为主要的燃料，为持续的火烧过程提供动力[3]。采出的原油是高温条件下裂解或挥发的重油轻质组分，相比地层原油，油品有较大程度的提升[4]。一般根据反应温度特征及产物类别，可将火驱过程划分为低温氧化、热裂解(中温氧化)和高温氧化3个反应阶段[5-6]。在油藏条件下注空气火烧油层，主要反应类型为加氧反应和断键反应。加氧反应主要发生在低温氧化阶段，断键反应主要发生在热裂解和高温燃烧阶段[79]。在燃烧过程中，稠油的高温氧化反应是驱动燃烧前缘稳定向前推移的主要影响因素，这一阶段对火烧油层成功与否起着决定性作用[10]。因此，对稠油高温氧化反应动力学参数进行分析，对研究火烧油层内在机理具有重要的现实意义。

蒋海岩等开展了基于阶段演化特征的稠油氧化动力学研究，采用Coats-Redfern积分法及Flynn-Wall-Ozawa(FWO)等转化率法计算了高温氧化动力学参数，并指出FWO法计算稠油氧化反应的活化能时，应将整个热重过程划分为不同的反应阶段，选择阶段性起止温度对应的质量作为计算活化能的基础数据[11-12]。唐君实等研究了使用热重分析仪求取稠油高温氧化动力学参数的方法，探讨了单一扫描速率法(Coats-Redfern积分法和ABSW微分法)，以及FWO等转化率法，并将计算结果进行对比，发现单一扫描速率法拟合的动力学数据存在一定程度的偏差，进而认为FWO等转化率法适用于油焦燃烧本征动力学的计算[13]。时光应用FWO法分别计算了稠油低温氧化、热裂解和高温燃烧阶段的活化能，与蒋海岩的研究方法一致[14]。Vyazovkin等论述了常用的基于热分析数据的动力学参数计算方法，认为FWO等转化率法计算结果的精度不足，推荐使用KAS法及其他精度更高的计算方法[15-17]。

由此可知，在利用热分析数据计算原油氧化动力学参数时，选取合适的计算方法对结果的准确性是十分重要的。该文在获取热重(thermogravimetry，TG)、微商热重(derivative thermogravimetry，DTG)、差示扫描量热数据(differential scanning calorimeter，DSC)的基础上，应用不同的计算方法对稠油高温氧化动力学参数进行分析，为进一步开展火烧油层机理研究奠定基础。

1 稠油火烧油层热分析实验

1.1 实验样品

选取辽河油田普通稠油进行热重、微商热重和差示扫描量热实验，原油的基本性质见表1。其中，稠油黏度用HAAKE VT550型旋转黏度计在规定温度下测定，50℃和80℃的黏度分别为1 670 mPa·s和98 mPa·s;稠油族组分按照NBSHT 0509-2010石油沥青四组分测定法进行测定，饱和烃、芳香烃、胶质和沥青质的含量分别为23.58%，27.79%，23.66%和24.97%。模拟砂选用100～150目的惰性SiO2。

表1 稠油的基本性质Table 1 The basic properties of the heavy oil sample

1.2 实验设备及方法

实验使用的热分析仪器如图1所示，其称重精度为±0.01%，温度为室温至1 000℃，加热速率为0.01～100℃/min，可实现自动气体切换和流量控制。利用热天平在程序制的升温速率下测量稠油氧化反应中质量随时间和反应温度的变化，并将其处理为转化率随温度的变化。

图1 热重分析实验仪Fig.1 TA instrument system

唐君实等在使用纯油样品进行热重分析时，发现油样结焦后内部无法形成有效且规则的气体流通，样品很难处于均匀反应状态，在高温氧化区出现反应速率多峰的现象，并建议使用油砂混合物进行热重分析[13]。该文采用油砂混合的方式制备样品，实验方法如下:

1)将原油过滤除杂、加热脱水后，在烘箱中120℃的条件下加热1 h;

2)原油从烘箱取出后，与模拟砂按1∶4的质量比进行均匀混合;

3)将模拟砂放在烘箱中，在120℃条件下恒温1 h，然后取出搅拌均匀，重复2次;

4)在混合好的样品中取出50 mg，放入坩埚并置于热分析仪内;

5)在常压且空气流通环境下进行，选取氮气作保护气，每次实验均设定氮气为20 m L/min的恒定质量流量，使气体充满整个反应室中后覆盖坩埚表面;

6)将程序升温的范围设定在20～600℃之间，升温速率分别设定为2℃/min，5℃/min，8℃/min。当温度和流量稳定时开始测试，当温度达到600℃时完成测试。

1.3 动力学参数计算方法

基本反应动力学方程可以写成:

对其作等温条件的积分得到:

式中:α为转化率，百分数或小数;t为反应时间，s;A是频率因子，又称指前因子，单位与反应级数有关;E为活化能，kJ/mol;R是摩尔气体常量，取值为8.314 J/(mol·K);T为热力学温度，K;f(α)为反应机理函数;g(α)是机理函数的积分形式。

1.3.1KAS等转化率法

对式(1)进行简单重排就可以得到Friedman的方法[18]:

式中:指数i表示单个加热速率，Tα，i表示在第i个加热速率下达到转化率α的温度，K;Eα是转化率为α时的表观活化能，kJ/mol。

对于任何给定的α，可根据式(3)对1/Tα，i的斜率来计算Eα的值。式(3)不仅适用于线性加热程序，而且适用于任何温度程序。

积分数据应使用由式(2)的积分形式得到的积分等转化率方法来处理:

如果温度以恒定的速率上升，即:

式中:βi是升温速率，℃/min或K/min。

当随时间变化的积分被温度的积分所取代时，式(4)变为:

式中:T0为加热开始时t=0处的初始温度，K。

温度积分I(E，T)没有解析解，可以用某个近似函数代替，也可以用数值积分来解决。传统的积分方法依赖于近似函数S(T)来表示在积分限0～T内估计的积分值，即:

式(6)中的I(E，T)应等于积分的不同上限T和T0所估计的近似函数值之差:

传统的积分方法通常忽略S(T0)，即从0～T0的积分。这相当于假设0～T0之间的过程热率可以忽略不计，这种假设在活化能相对较高的情况下是合理的。当所讨论的过程具有较低的活化能，并且在接近初始温度下的温度可以被检测到时，忽略从0～T0的积分，可能会导致活化能的计算值出现较大的误差。

对于稠油的高温氧化反应，活化能较高，满足忽略S(T0)的条件。忽略S(T0)的方法可以统一表示为:

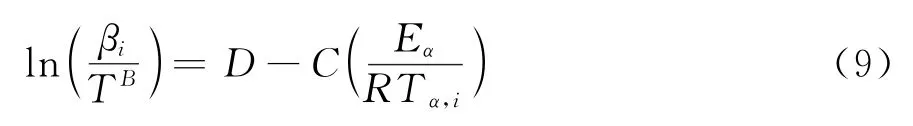
式中:B和C是由温度积分近似式确定的常数;D为常数;Eα值可由ln(βi)相对于1/Tα，i拟合直线的斜率求得。取不同的α值，重复该过程会发现Eα对α的相关性。当B=0，C=1.052时，式(9)即为FWO等转化率法。

KAS等转化率法相比FWO等转化率法具有更高的精度。KAS等转化率法通过以下公式计算各阶段反应动力学参数[19]。相应地，当B=2，C=1时，式(9)即变为KAS等转化率的表达式:

式中:T为绝对温度，T0和T f分别为初始温度和终了温度，K。

当α为定值时，g(α)值不变，可对不同升温速率下的ln(β/T2)和1/T作线性回归，得到的直线斜率为，而截距为，由此可求出表观活化能Eα的值。Eα值确定后，假设一个机理函数g(α)，对ln(β/T2)和ln[g(α)]以最小二乘法拟合，斜率接近-1且相关系数接近1的机理函数即为该阶段反应的最概然机理函数。当表观活化能和机理函数确定后，指前因子可根据截距计算。

1.3.2 Kissinger微分法

除上述方法外，Kissinger微分法可根据差示扫描量热曲线求取反应动力学参数，其反应机理函数为:

式中:n是反应级数，可以是整数或分数。在化学反应的速率方程中，各物浓度项的指数的代数和就是该反应的级数，反应级数由化学反应机理决定。

将式(12)代入到基本反应动力学方程有:

通过对式(13)微分，得到:

对应差示扫描量热曲线上峰值温度T=T p，此时的反应速率最大，有，得到:

式中:T p为峰值温度，K;αp为峰值温度对应的转化率。

一般认为n(1—αp)n-1与升温速率无关，其值约等于1，式(15)因而可变为:

对式(16)取对数，得到Kissinger微分法的表达式:

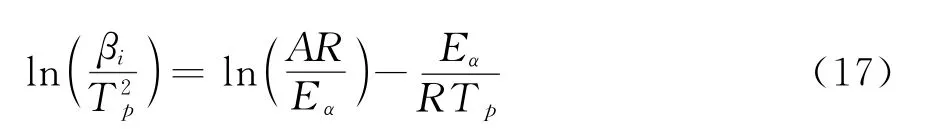
1.3.3 Coats-Redfern积分法

Coats-Redfern法是积分法中最具有代表性的方法之一，基本公式为:

对上式积分，并进行近似处理，得到:

n=1时

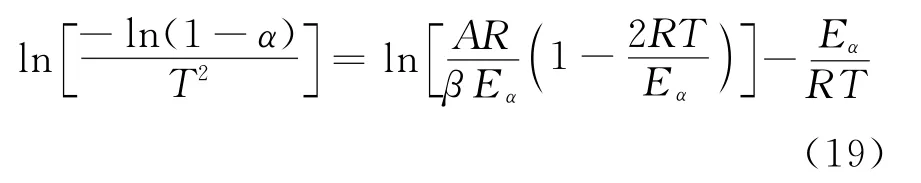
n≠1时:

当n=1时，对1/T线性拟合，当n≠1时，对1/T线性拟合，分别由斜率求取活化能。值得注意的是，不同反应的反应级数n并不相同，需要针对不同的反应级数进行计算，由线性度最好的n值，确定最终的反应级数。

2 实验结果与分析

2.1 热重/差示扫描量热曲线

稠油的热重和转化率曲线如图2所示，其中黑色实线和虚线分别为加热速率为2℃/min时的热重与转化率曲线，红色与蓝色曲线则为加热速率为5℃/min和8℃/min的结果。图3为加热速率为5℃/min条件下热重、差示扫描量热和微商热重曲线。

图2 不同加热速率下的热重和转化率曲线Fig.2 TG and conversion rate curves of the oil sands at different heating rates

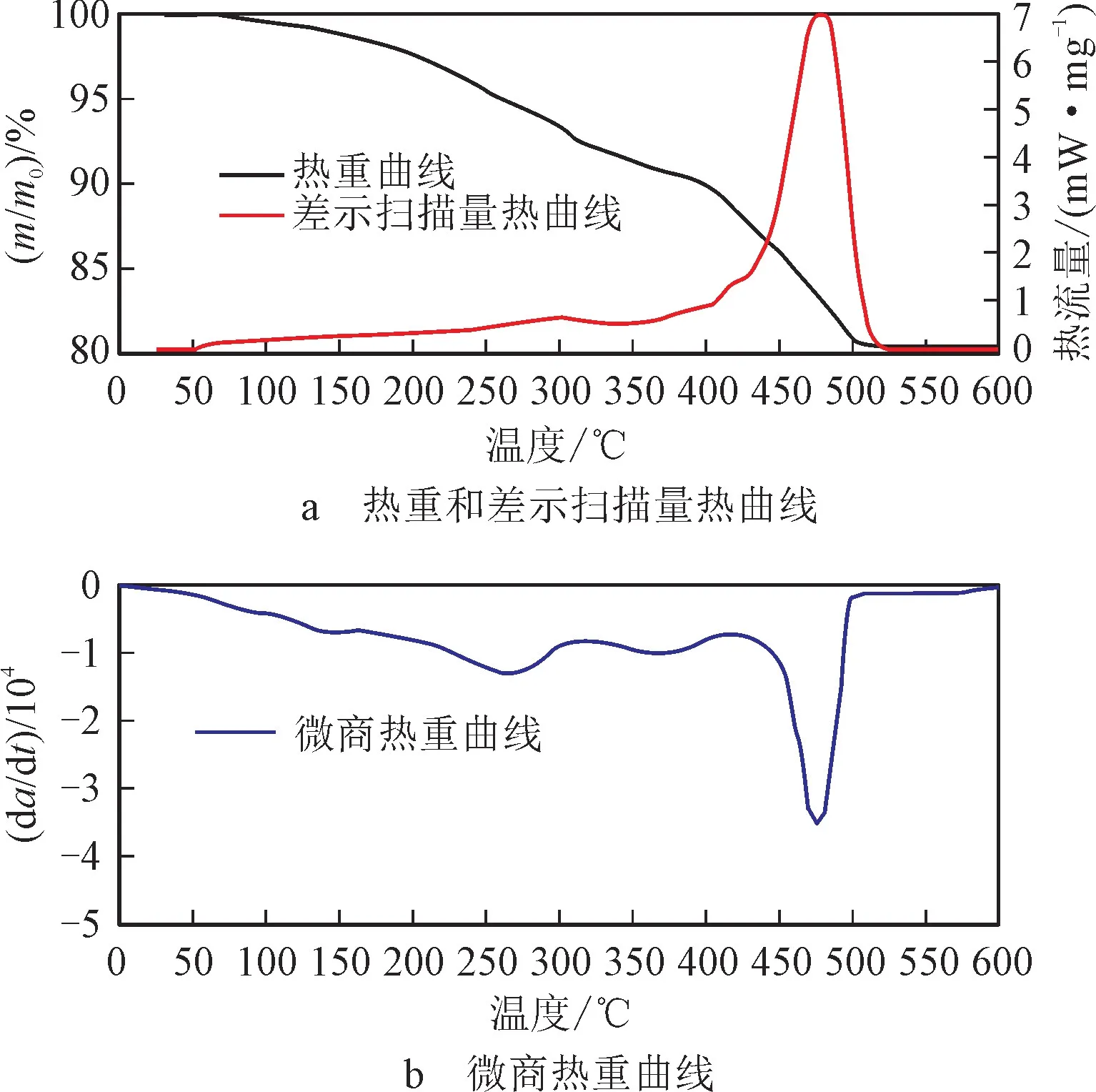
图3 加热速率为5℃/min时的热重、差示扫描量热和微商热重曲线Fig.3 TG，DSC and DTG curves of the oil sands at the heating rate of 5℃/min

结合图2和图3可知，稠油火烧过程中存在低温氧化、中温氧化(热裂解)和高温氧化温度区间，不同升温速率下氧化反应的阶段演化特征和参数见表2。在不同的升温速率下，热重曲线的形状基本保持一致，曲线产生的平移是由于随着反应速率增加，传热滞后效应导致的。其中，低温氧化反应前段主要以原油中的轻质组分和水分的蒸馏、挥发为主，伴随着少量的加氧反应，但此阶段的氧化断键反应并不占据主导地位，仅生成少量的长链碳氢。随着原油的氧化反应程度的加强，低温反应前段所生成的部分长链液态烃与后续的氧气继续发生反应。低温氧化阶段主要生成羧酸类、醛类、酮类化合物、有机过氧化物等，属于气液相边界反应。因此，低温氧化反应属于加氧反应，即使在较低的油藏温度下，也会随着氧气在原油中的扩散而发生。以加热速率5℃/min为例，低温氧化温度区间为125～313℃，符合Moore等所研究的低温氧化温度区间(低于315℃)[20]。在差示扫描量热曲线上，出现一个较小的放热峰，峰值温度为299℃。

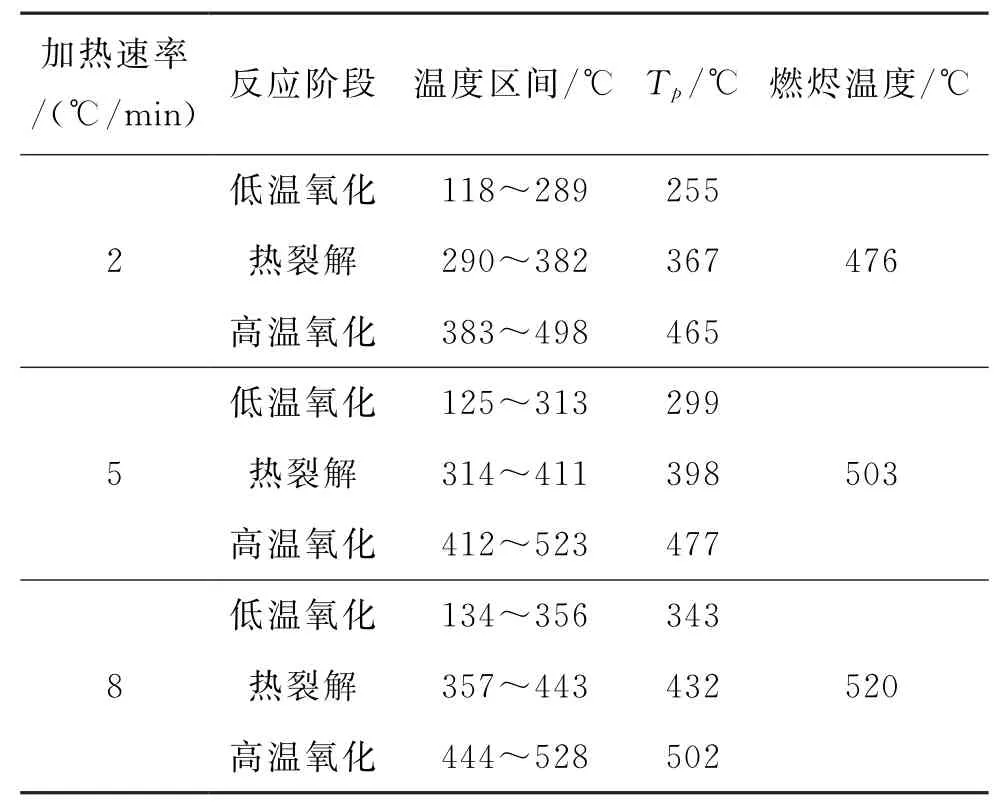
表2 不同升温速率下油砂反应阶段特征参数Table 2 Multistage characteristics parameters in of the oil sands at different heating rates

随着温度逐渐升高，反应速率显著加快。在高温氧化阶段，燃料开始燃烧，此阶段主要发生在热裂解阶段生成的油焦和氧气之间，稠油具有较高的活化能，燃烧生成大量的CO，CO2，H2O等气体，并释放大量的热，在差示扫描量热曲线上出现了较高的放热峰，峰值温度为477℃，燃烬温度为503℃。

2.2 KAS等转换率法分析结果

根据KAS等转换率方法，计算稠油高温氧化阶段的动力学参数。根据不同升温速率时稠油高温氧化反应的各特征参数，计算转化率，并根据相同转化率下不同升温速率时的温度，对多组升温速率及特征温度数据进行最小二乘法拟合，由此求取活化能。通过对不同转化率情况进行等转化率计算，发现随着转化率增加，直线斜率(绝对值)增加，表明反应活化能增加，这与实际情况一致。转化率为0.9时的拟合结果如图4所示，直线斜率为-18 493.8，相关系数R2为0.97，计算的活化能为153.7 kJ/mol，lnA为16.26，最概然机理函数为。根据最概然机理函数所揭示的机制，在高温反应阶段，随着相边界反应的基本消失，油焦与氧气开始充分接触，以三维扩散为主，持续发生反应，使燃烧处于扩散状态。氧气浓度梯度是影响三维扩散的主要因素，由此生成的物质以三维矢量方式进行过程传递。

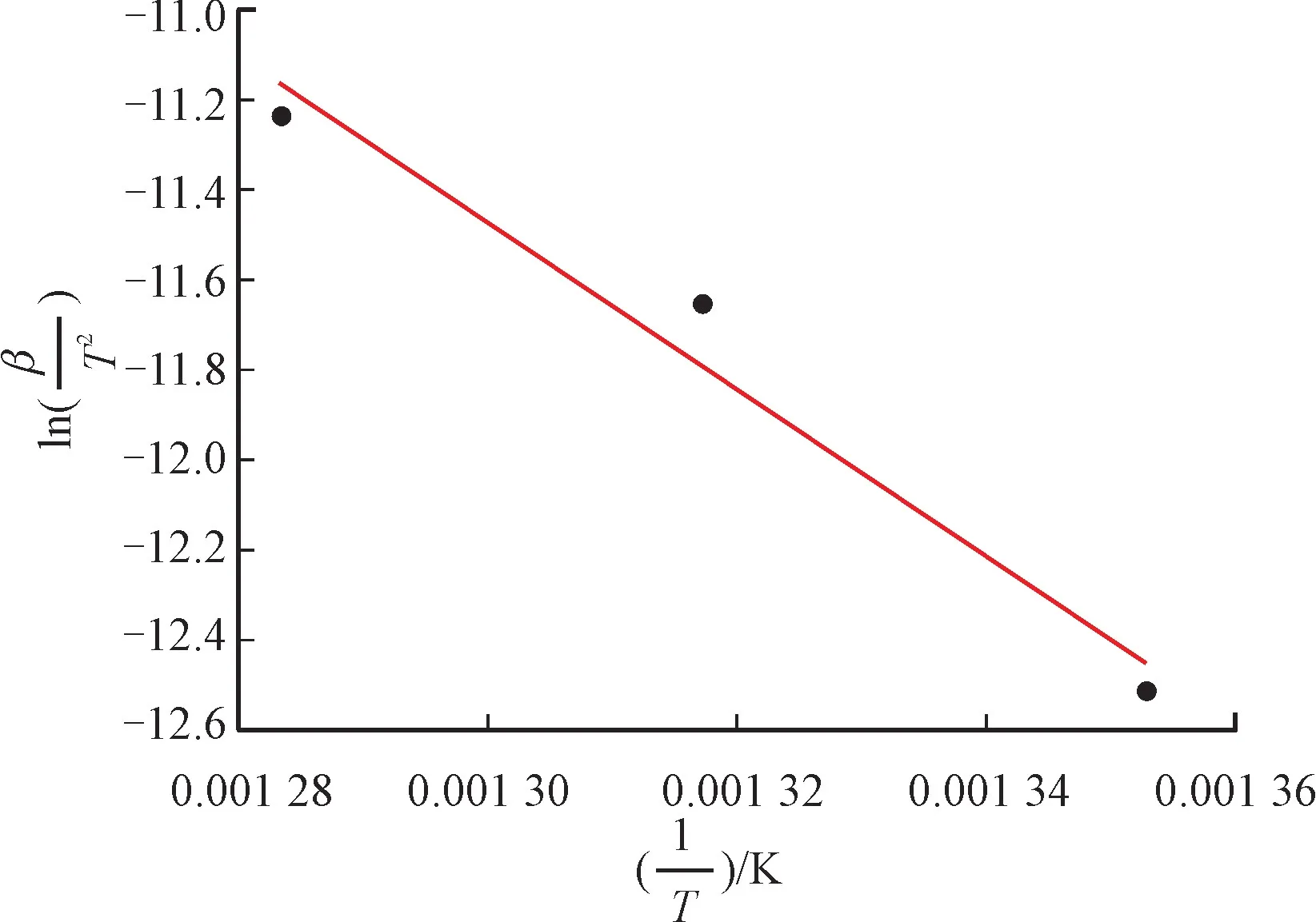
图4 转化率为0.9时高温氧化KAS拟合结果Fig.4 The KAS result of high temperature oxidation at the conversion rate of 0.9

2.3 Kissinger微分法分析结果

应用Kissinger微分法根据不同升温速率下的特征温度进行计算，对对1/T p进行线性拟合，如图5所示，斜率为-14 133.5，R2为0.96。计算的稠油高温氧化反应活化能为117.5 kJ/mol，lnA的值为16.4，Kissinger微分法计算的活化能值低于KAS法的计算值。由于KAS法所选取的转化率为0.9，由可变活化能的意义可知，在转化率较高时一般活化能较高[17]。Kissinger微分法选取特征温度T p，以升温速率为5℃/min为例，特征温度对应的转化率为0.85，因此活化能值低于KAS法计算值。此外，由于Kissinger微分方程是基于假设条件的简化方程，精度偏低，也是导致活化能计算值较低的原因。

图5 Kissinger微分法拟合结果Fig.5 The fitting result of Kissinger differential method

2.4 Coats-Redfern分析结果

采用Coats-Redfern积分法计算火烧稠油的氧化动力学参数，结果如图6所示，其中红色为反应级数n=1时对1/T的关系曲线，黑色分别为n=0.5，1.5和2.0的对1/T关系曲线。从图中可以看出，稠油火烧的过程非常复杂，在实验温度区间内，对1/T不是单一的直线，而是在某一阶段呈现直线特征，这对应了稠油火烧过程中的低温氧化、热裂解和高温氧化的不同阶段，表明了稠油氧化过程的阶段演化特征。应用Coats-Redfern积分法对低温区间和高温区间分别进行拟合，结果显示，在高温氧化反应区间，且在较高的反应级数(n=2)时拟合结果较好，计算的高温氧化反应活化能为147.6 kJ/mol。图7为反应级数n=2时，高温氧化反应的lnA与1/T的拟合曲线，相关系数R2为0.990 5，拟合效果较好。

图6 升温速率为5℃/min的Coats-Redfern积分法曲线Fig.6 The Coats-Redfern curves at the heating rate of 5℃/min

图7 ln A与1/T拟合结果(n=2)Fig.7 The fitting result of ln A and 1/T by the Coats-Redfern method

3 结论

1)应用KAS等转化率法、Kissinger微分法和Coats-Redfern积分法求取的稠油高温氧化反应动力学参数(活化能值和频率因子值)均在正常范围内，线性相关系数均在0.95以上，满足计算精度要求。

3)Coats-Redfern积分法计算的曲线反映了稠油火烧过程中的低温氧化、热裂解和高温氧化的阶段演化特征。应用Coats-Redfern积分法对稠油高温氧化反应的拟合效果较好。

4)KAS等转化率法和Coats-Redfern积分法计算的活化能值接近，而Kissinger微分法计算的活化能值略低，3种方法所计算的频率因子值比较接近。