智慧农业中时序数据组合预测模型
陈晓雷,王星星,申浩阳
(郑州轻工业大学计算机与通信工程学院,河南 郑州 450001)
0 引 言
所谓时间序列,是指以时间顺序取得的一系列观测值。时间序列分析是指对时间序列进行预测分析,在现实生活中被广泛应用[1]。近年来,国内外的很多学者提出或改进了基于时间序列的预测方法,应用在公共交通[2-4]、社会经济[5-7]、环境监测[8-10]、医学研究[11-12]等行业。
考虑一个时间序列可能会同时存在线性关系和非线性关系,预测方法有线性预测模型和非线性预测模型之分。国内学者大多采用传统的ARIMA模型和神经网络的结果组合模型来进行预测,例如张鹏[13]提出了ARIMA-GM-SVR非线性组合模型,并用PSO进行优化;李存祖[14]提出了基于ARIMA-BP-SVM混合预测模型;李鹏飞等[15]提出了一种基于ARIMA-Kalman滤波混合算法,用来预测苹果产量;张冬雪[16]提出了一种基于LSTM和ARIMA的风速时间序列预测模型,在预测精度上有较小提升;田东等[17]从挖掘温室历史温度数据信息的角度出发,提出了MA-ARIMA-GASVR组合预测模型来模拟温室温度的未来趋势。国外的学者大多利用改进的神经网络模型来实现预测,例如Budi等[18]改进了LSTM神经网络模型,并应用于智慧农业系统中;Tormozov等[19]用遗传算法优化后的神经网络模型预测时间序列;Ustundag等[20]提出了一种具有预测误差补偿的小波神经网络模型预测时间序列。
本文基于智慧农业系统对时间序列预测精度的要求以及以上学者的相关研究,提出一种基于差分整合移动平均自回归模型和小波神经网络的组合预测模型,根据某温室内历史温度数据对未来一段时间的温度值进行预测。温室内的温度数据特征复杂,用单项模型进行预测,结果会产生较大误差。将差分整合移动平均自回归模型与神经网络组合,可以充分发挥2种模型各自的独特性和优势,通过对线性部分建立差分整合移动平均自回归模型,非线性部分建立神经网络模型,再将2种模型的结果结合,相对单项模型,提高了预测精度,并且得到的预测结果与实际值的拟合度更高。
1 时间序列的组合预测模型
1.1 差分整合移动平均自回归模型
差分整合移动平均自回归模型(Autoregressive Integrated Moving Average Model, ARIMA)是针对时间序列建立因变量对序列的滞后值和序列随机误差项的当前值及滞后值的回归模型[21]。序列应满足平稳性或差分处理后满足平稳性的要求[22],否则ARIMA模型无法捕捉规律。
ARIMA 模型就是AR模型和MA模型,再加上一个差分组合起来的模型。AR 为自回归模型,MA 为移动平均模型。ARIMA 模型可简写为(p,d,q)模型,p为数据本身的滞后数,q为预测误差的滞后数。p和q的取值要通过对自相关函数图(Autocorrelation Function, ACF)和偏自相关函数图(Partial Autocorrelation Function, PACF)的分析得到。d代表时序数据稳定时,所进行的差分化阶数,差分的阶数即为d的取值。
1)自回归模型。
自回归(Auto-Regressive, AR)模型利用当前值与历史值的关系来预测当前值。使用自回归模型预测的数据必须是平稳的。自回归模型首先需要确定阶数p的值。p阶自回归模型公式定义为:
(1)
其中,at是当前值,α是常数项,γi是自相关系数,εt是误差。
2)移动平均模型。
移动平均(Moving Average, MA)模型关注自回归模型中的误差项(白噪声)的累加,能有效消除预测中的随机波动移动。平均模型需要一个移动平均项数q,故该模型一般写作MA(q),其公式为:
(2)
其中,bt是当前值,β是常数项,θi是相关系数,εt是误差。
3)差分整合移动平均自回归模型。
将AR模型和MA模型组合,就可以得到移动平均自回归模型ARMA(p,q),如式(3):
(3)
其中,yt是当前值,δ是常数,εt是误差。
采用ARMA模型预测的时间序列必须为平稳的,若为非平稳序列,需要先经过差分化为平稳时间序列,然后再建立ARMA模型。
1.2 小波神经网络的预测模型
神经网络是分析多个问题的一种替代或补充技术,这些问题通常涉及未知的或非线性关系[23]。小波神经网络(Wavelet Neural Network, WNN)是在BP神经网络拓扑结构的基础上,把小波基函数作为隐含层节点的传递函数,信号前向传播的同时误差反向传播。其拓扑结构如图1所示。
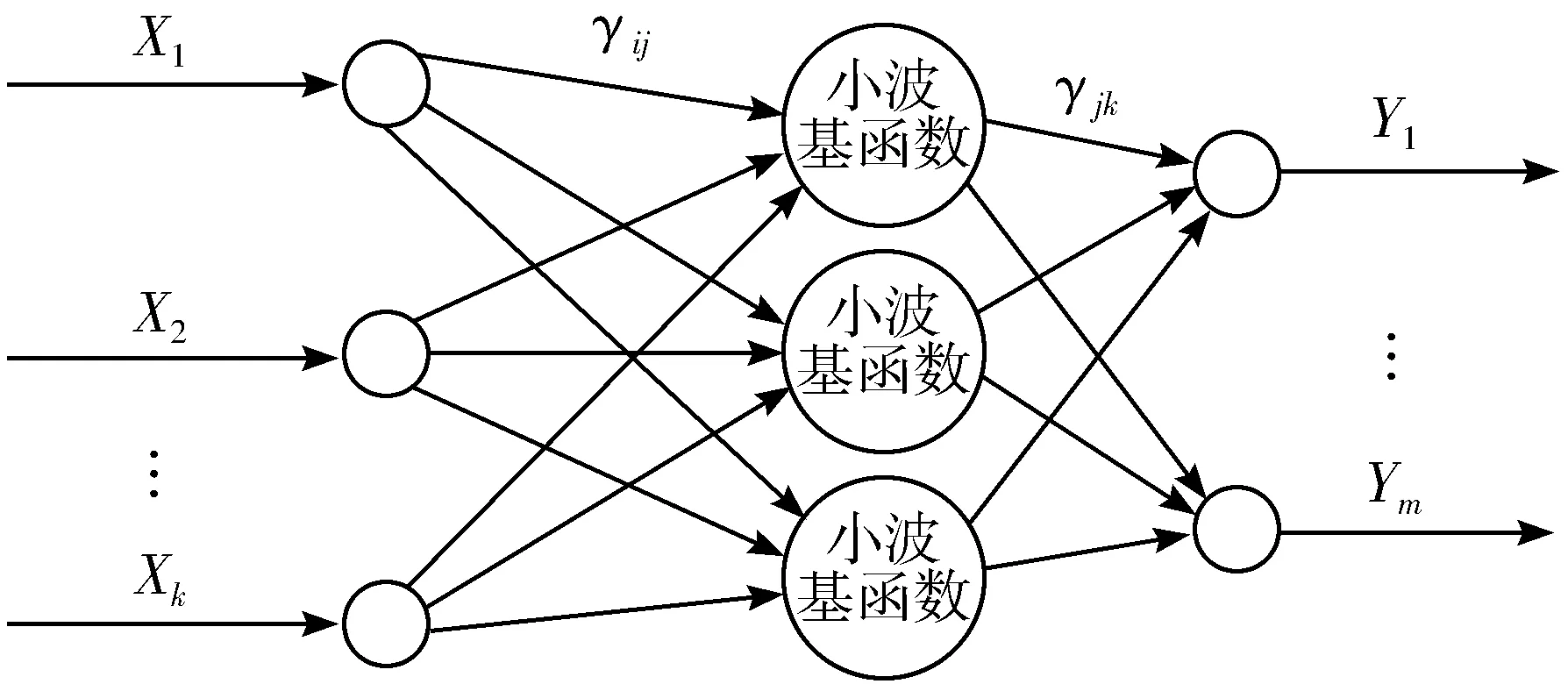
图1 小波神经网络拓扑结构
图1中,X1,X2,…,Xk为输入参数,Y1,Y2,…,Ym为预测输出,γij和γjk为权值。
在输入信号序列为Xi(i=1,2,…,k)时,隐含层输出计算公式如式(4):
(4)
其中,h(j)为隐含层第j个节点输出值;hj为小波基函数;γij为输入层和隐含层的连接权值;bj为hj的平移因子;aj为hj的伸缩因子。
WNN输出层计算公式如式(5):
(5)
其中,γjk为隐含层到输出层权值;h(j)为第j个隐含层节点的输出;l为隐含层节点数;m为输出层节点数。
WNN权值参数修正算法是用梯度修正法来修正网络的权值和小波基函数参数,使小波神经网络预测值不断接近实际值,修正过程如下:
1)计算网络预测误差:
(6)
其中,yn(k)为期望输出;y(k)为小波神经网络的预测值。
2)根据预测误差e修正小波神经网络权值和小波基函数系数:
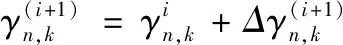
(7)
(8)
(9)
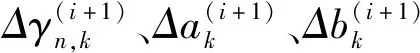
(10)
(11)
(12)
其中,η为学习概率。
WNN算法训练步骤为:
1)网络初始化。随机初始化小波函数伸缩因子ak、平移因子bk以及网络连接权重γij、γik,设置学习效率η。
2)样本分类。把样本分为2类:训练样本和测试样本。训练样本用于训练网络,测试样本用于测试网络的预测精度。
3)预测输出。把训练样本输入网络,计算网络预测输出及网络输出和期望输出的误差e。
4)权值修正。根据误差e修正网络权值和小波函数参数,使预测值更接近于期望值。
5)判断算法是否结束,若没有结束,返回步骤3。
1.3 基于ARIMA和WNN的组合预测模型
组合预测模型就是采用适当的方法组合多个单项预测模型,对各种单项模型的预测效果进行综合处理,生成一个含有多个预测模型和预测信息的总预测模型。在实际中预测问题往往是比较复杂的,因为预测问题受到众多因素的影响,而且这些因素可能是不确定的,一个模型不足以处理具有未知混合模型的复杂现实世界系。此时,组合模型就能发挥优势,通过信息集成的方法来降低或分散单项预测模型含有的不确定性,最大效率地利用单项模型的有效信息。
对于一个时间序列{yt},认为它是由一个线性自相关部分Lt和一个非线性部分Nt组成,即:
yt=Lt+Nt
(13)
其中,Lt和Nt是根据时间序列数据进行估计。该组合模型的预测步骤为:
1)对数据进行预处理。经过预处理后的数据,能够缩短模型预测的时间,提高预测精度。
2)利用ARIMA对该序列的线性部分建模,原序列中的非线性关系存在于残差部分。令et为t时刻线性模型的残差,则:
et=yt-L′t
(14)
其中,L′t为通过ARIMA建模在t时刻的预测值。
3)对残差序列{et}建立小波神经网络模型,对于有n个输入节点的小波神经网络模型,残差计算为:
et=f(et-1,et-2,…,et-n)+εt
(15)
其中,εt为随机误差,非线性函数f通过神经网络来逼近,得到t时刻的残差预测结果记为N′t。
4)将2种模型结合,即:
y′t=L′t+N′t
(16)
由于ARIMA模型不能描述数据的非线性结构,而经ARIMA模型预测后的残差项为非线性结构,能够捕捉非线性关系的神经网络模型正好可以用于误差项的预测。将2种模型的结果组合,可以改进ARIMA模型的预测精度。
2 模型仿真
本次实验采用某温室内连续2 h采集到的温度数据。由于在短时间内,温室内的温度变化较小,所以将数据采集间隔设为1 min,2 h采集到一组样本容量为120的温度数据,图2为原始数据的变化趋势图。
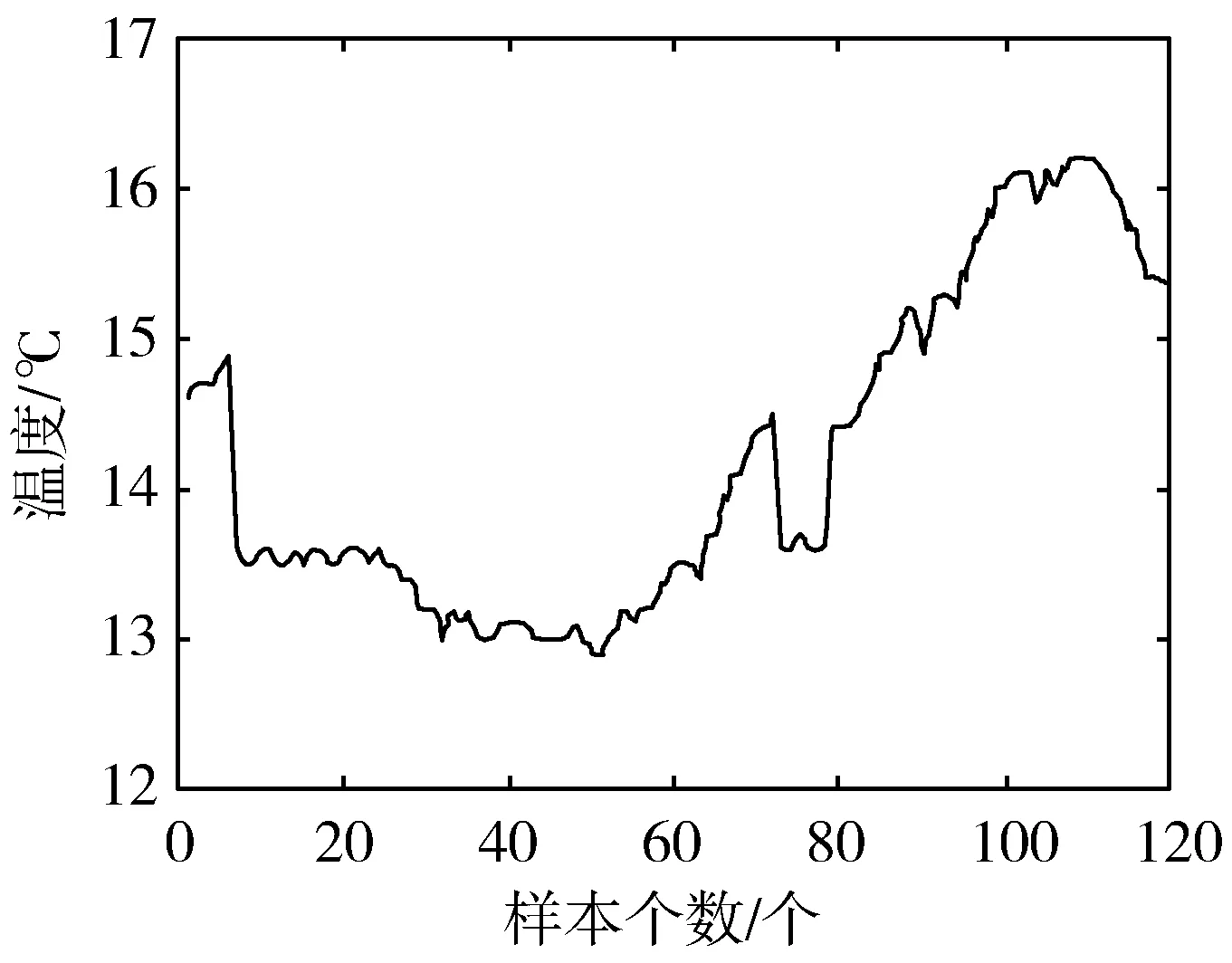
图2 原始数据变化趋势图
1)数据预处理。
在进行预测前,要先对数据预处理,将采集到的数据统一规范。其规范化公式为:
(17)
其中,maxy(i),miny(i)分别为数据流y(i)的最大值和最小值。
2)ARIMA模型建模。
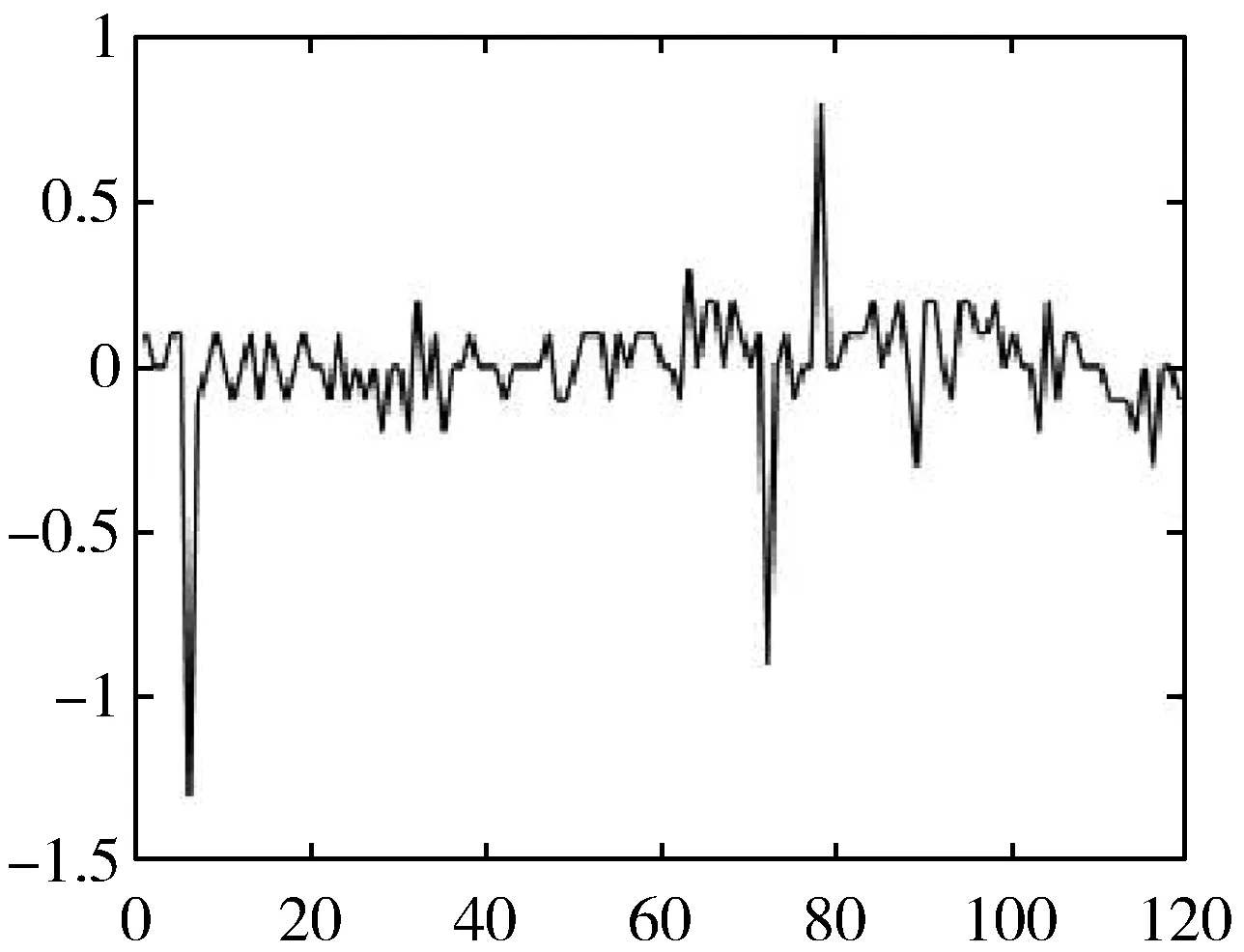
在进行模型预测前,先要判断该数据序列是否平稳。由图2可以判断该数据序列并不平稳,但在某些情况下该方法难以判断序列是否平稳,针对此次的样本序列,肉眼观察后判断为非平稳序列。为准确起见,再采用单位根检验(Augmented Dickey-Fuller test, ADF)验证上述结论。检验结果显示单位根存在,则该序列为非平稳序列,需进行差分处理为平稳序列后,才能进行下一步的预测。图3为样本序列差分后的图像。
(a) 一阶差分序列
由图3可知,本次实验所使用的数据流经二阶差分后序列图像趋于平稳,ADF检验值为0,可以判定出差分阶数。找到差分阶数并平稳化序列后,做出序列的ACF图和PACF图,以判断和的值,分别如图4和图5所示。
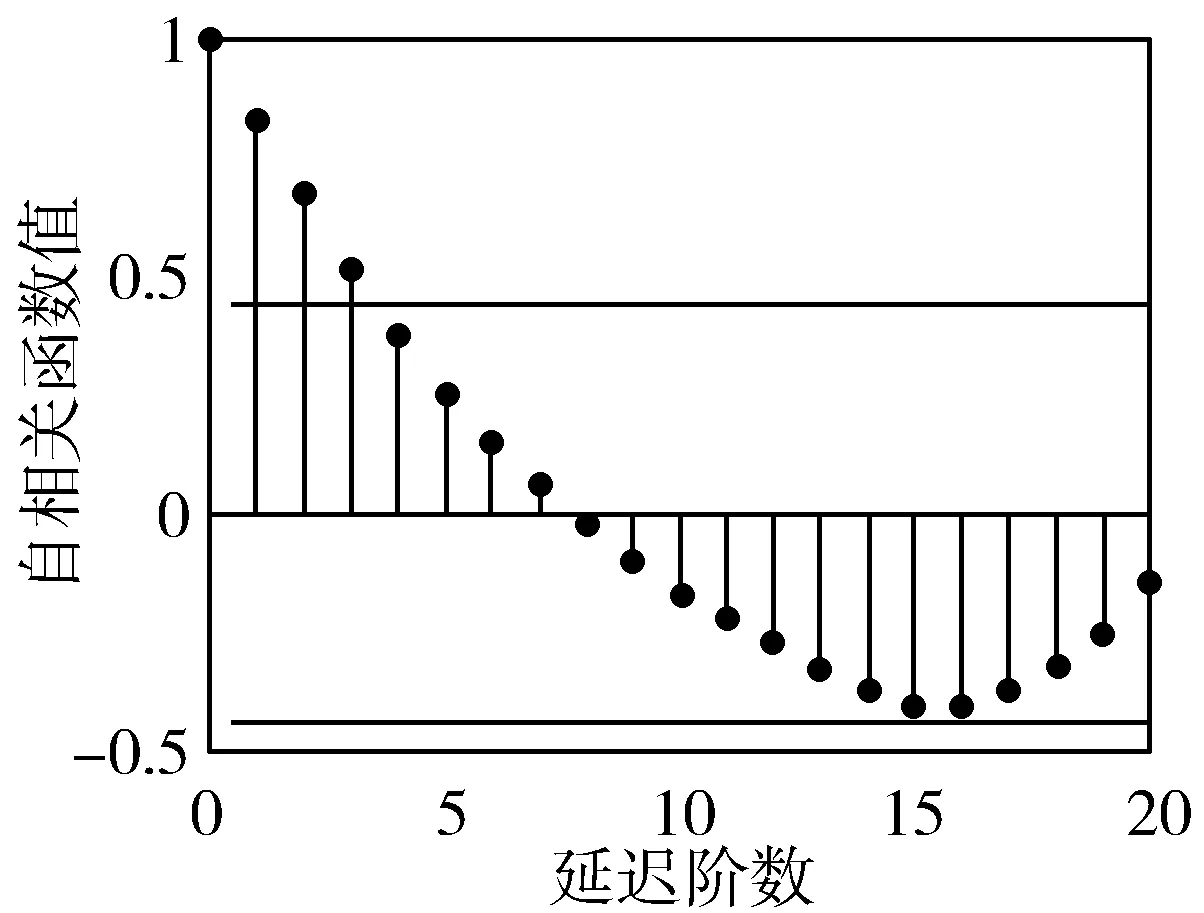
图4 自相关函数图

图5 偏自相关函数图
由图4可得q=4,由图5可得p=2,故得该预测模型为ARIMA(2,2,4)。图6为由该模型所得的预测结果和实际值的对比结果图。由图6看出,ARIMA模型能很好地模拟实际值的变化趋势,但随着预测步骤的增加,在预测精度上有较大的误差,需要进一步优化。
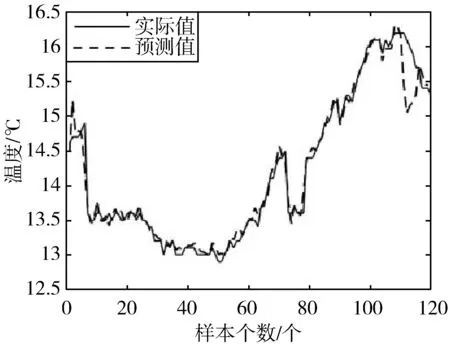
图6 ARIMA模型的温度预测值与实际值对比
3)WNN模型优化残差。
神经网络的隐含层节点数的多少会对预测精度产生一定的影响,节点数过多或过少,都会有较大的误差,最佳隐含层节点数可由如下公式确定:
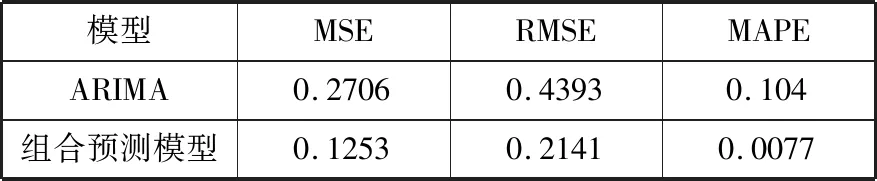
l (18) (19) l=log2n (20) 其中,n为输入层节点数;l为隐含层节点数;m为输出层节点数;a为0~10之间的常数。本次实验中,l的值为3,式(21)为小波基函数: (21) 获取残差数据后,初始化小波神经网络结构、权值和小波基函数参数,并对训练数据进行归一化处理。使用小波神经网络对训练数据进行迭代,得到的残差值序列优化前后的对比结果如图7所示。 由图7可知,经WNN优化后的残差值虽然在预测前期有较大的波动,但随着训练次数的增加,波动幅度与优化前相比更小,可以用于ARIMA模型残差的修正。 图7 WNN模型的残差值预测值与实际值对比 4)组合预测模型建立。 基于ARIMA对原始数据序列线性部分的预测值和WNN对残差序列的预测值,由式(16)可以得到组合后的预测值。传统的ARIMA模型和组合预测模型得到的预测值与实际值之间的对比结果如图8所示。 图8 2种模型的温度预测值与实际值对比 由图8可知,与ARIMA模型相比,组合模型的预测结果和实际值更加贴近,在趋势上与实际值大致相同。下面用均方误差(Mean Square Error, MSE)、均方根误差(Root Mean Square Error, RMSE)和平均百分比误差(Mean Absolute Percentage Error, MAPE)这3个指标来评价所研究的模型。3个指标的数学表达式分别为: (22) (23) (24) MSE用来评价数据的变化程度,RMSE表示误差的平方的期望值,MAPE表示预测模型的精确度,这些评价指标的值越小,相应预测模型的预测值与实际值相似度越高,只是在使用MAPE时观测值不能为0,当存在分母为0的情况时,该公式不可用。表1为ARIMA模型和组合预测模型针对3个评价指标的对比结果。 表1 评价指标的对比结果 根据表1以及评价指标的性质可以看出,经WNN模型优化ARIMA残差后的组合模型,其MSE和RMSE值明显小于ARIMA模型,分别为0.1253和0.2141,表明这个组合模型的精确度更高,其MAPE的值为0.0077,与ARIMA模型的MAPE值相比更接近于0,说明该组合模型的拟合效果更好。综合3个评价指标及预测输出变化趋势,将ARIMA和WNN组合后的模型预测精度更高,拟合效果更好,在预测温度趋势的应用中有良好的效果。 本文考虑到样本数据之间可能同时存在线性关系和非线性关系,提出了一种基于ARIMA和WNN的组合预测模型,将农作物温室内连续时间内采集到的温度数据作为实验样本,用ARIMA来预测样本数据的线性关系,用WNN来优化其残差所包含的非线性关系,最后将两者结合,得到最终的预测结果。与传统的ARIMA的预测结果相比,基于ARIMA和WNN的组合预测模型具有更高的预测精度和拟合能力,能够满足智慧农业中对相关序列的预测要求。但该模型仍有需要改进的地方,接下来的工作将进一步改进不足之处,并验证该组合模型在其他环境指标(如湿度)上的可推广性。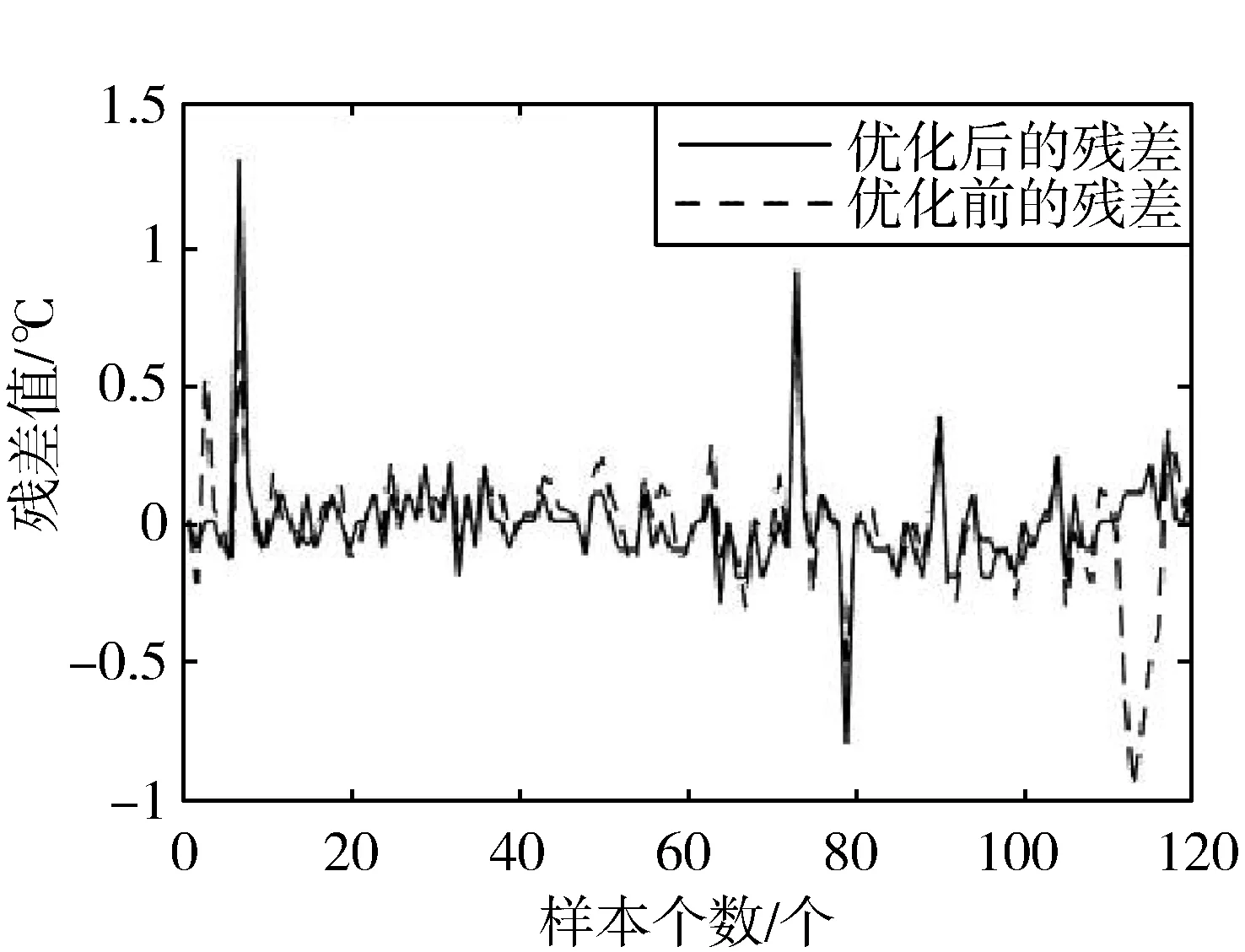

3 预测模型评价
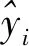
4 结束语

