刮刀离心机刮料转臂的疲劳分析*

王学永

(广州广重分离机械有限公司，广东 广州 511495)

0 引 言

刮刀离心机转臂是实现刮料动作的主要受力部件，承受循环载荷作用，易出现疲劳破坏，疲劳破坏是导致结构和机械失效的主要因素之一，引起疲劳失效的循环载荷的峰值远小于静态断裂计算出来的载荷。因此，进行结构疲劳分析有着重要的实际意义。

目前，国内外对结构疲劳损坏相关的分析较多，而针对虹吸刮刀离心机转臂的分析较少。文献[1]以香蕉型振动筛为研究对象，考虑影响疲劳的因素对材料的S-N曲线进行了修正，得到修正后的振动筛的S-N曲线，并基于静力分析的基础上，对振动筛进行了疲劳分析，获得了振动筛的疲劳寿命。应力集中是影响结构疲劳的最显著因素，文献[2]介绍了获取应力集中的三种常规方法，对比发现有限元方法求解结构的理论应力集中系数不受材料及结构条件的限制，省时、省力且成本低，结果精确可靠。有限元法对复杂结构进行静力及疲劳分析是一种极为有效的数值计算方法[3-6]，为转臂的疲劳分析提供了有力的工具。笔者基于有限元分析软件ANSYS对GKH1800-N型离心机转臂进行了疲劳分析，得到了转臂的疲劳寿命，为分析转臂的疲劳损坏提供了参考依据。

1 转臂模型

转臂几何结构如图1所示。刮料转臂由螺钉固定在刮料斗一侧的端面上，刮料斗由门盖上的径向滚子轴承支撑。在油缸的推动下，转臂与刮料斗一起旋转，实现刮料功能。转臂、螺钉及刮料斗的材料特性[7]，如表1所列。

图1 转臂几何结构 图2 转臂有限元模型

表1 材料特性参数

利用ANSYS软件建立包含转臂、螺钉及刮料斗的有限元模型，如图2所示。

转臂、螺钉及刮料斗均采用8节点六面体单元离散；为减少计算成本，不考虑螺钉螺纹牙型的实际结构，按螺钉的危险截面创建螺杆，螺钉与刮料斗建成一体模型；螺钉头部与转臂贴合面之间创建接触对，转臂与刮料斗贴合面之间创建接触对；文中研究核心目标为转臂，为减少计算成本，刮料斗仅建立与转臂贴合端及安装轴承部位的一段完整连续的局部模型，以模拟刮料斗对转臂的反作用力。

在转臂驱动端圆柱孔几何中心位置创建节点，使该节点与圆柱面上的所有节点自由度耦合，以施加油缸对转臂的推力载荷；在刮料斗安装轴承位置的圆柱面几何中心处创建节点，使该节点与该圆柱面上的所有节点自由度耦合，以施加轴承对刮料斗的约束。

整个模型的节点总数为277621个，单元总数为263907，其中，8867个接触单元，2个质量单元。

2 静力分析

刮刀离心机是间歇式离心机，每个工作循环有进料、脱水及刮料3个基本工况。在进料与脱水工况下，转臂不受油缸推力，仅受螺钉预紧所引起的压紧力；在刮料工况下，除了受螺钉预紧力外，转臂还受油缸推力及刮料斗的摩擦阻力距。由此可知，转臂在工作过程中受循环载荷作用。在对转臂进行疲劳分析之前，首先对其进行静力分析，并对上述轴承面的耦合节点约束全部自由度。

2.1 进料与脱水工况

在螺钉头部与卸料斗端面之间的螺钉柱体上施加预紧力，大小为78 400 N，方向沿螺钉轴线方向。计算结果如图3所示，最大等效应力为267.3 MPa，位于被螺钉头部端面压紧的环面上。

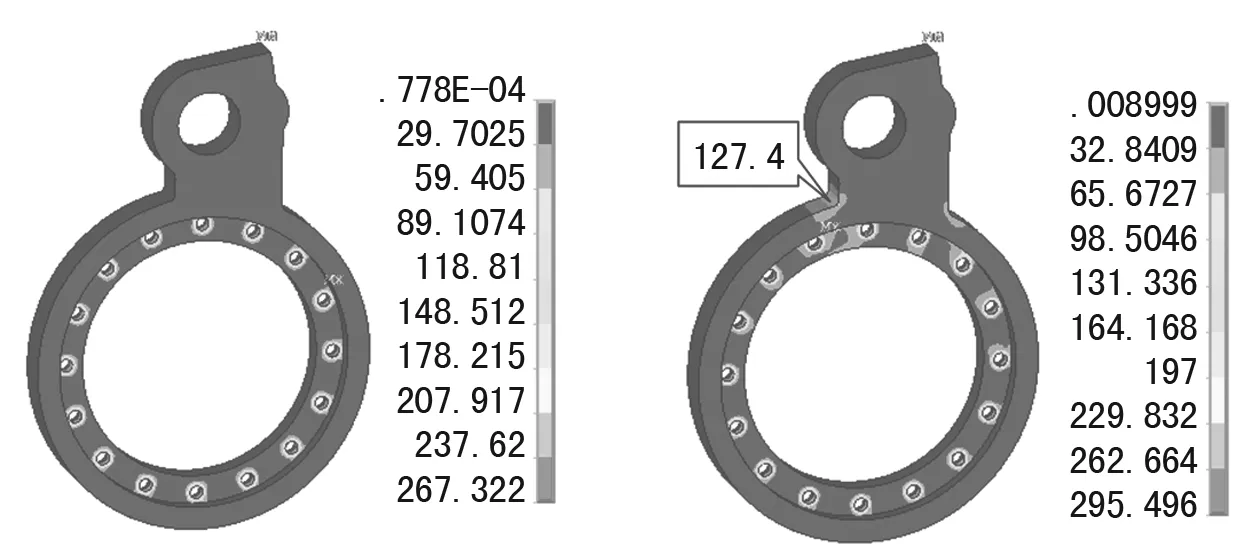
图3 进料与脱水时的应力状态 图4 刮料时的应力状态

2.2 刮料工况

在保持转臂上述工况的应力状态条件下，在转臂驱动端圆柱孔几何中心的耦合点处施加油缸推力，大小为73 631 N，方向垂直于两孔中心点的连线。计算结果如图4所示，最大等效应力为295.5 MPa，同样位于被螺钉头部端面压紧的环面上。

转臂的材质为调质处理的钢，其抗拉强度σb=833.6 MPa，屈服强度σs=686.5 MPa。上述两种工况下转臂的最大等效应力均小于材料的屈服强度，满足静强度设计要求。

3 疲劳分析

由刮料工况下的静力分析结果可知，转臂所受的最大等效应力位于被螺钉头部端面压紧的环面上，其次为转臂图示右侧的圆角处，分别为295.5 MPa、127.4 MPa。

对于环面应力，该应力是由螺钉预紧力及油缸推力共同作用所产生应力的线性叠加。对比两不同工况下的静力分析结果可知，螺钉预紧力引起的应力为267.3 MPa，则在此预紧力下油缸推力引起的循环应力为28.2 MPa，远小于转臂圆角处的循环应力127.4 MPa。而预紧力在工作循环中不发生变化为静态载荷，静态载荷不引起疲劳损坏。

另外，转臂圆角处的应力由循环载荷引起，且应力值远高于环面处的循环应力值，圆角处最易发生疲劳损坏。且从图1可看到，转臂裂纹的疲劳源也位于圆角处，且向螺钉头部端面压紧的环面延伸。对此，采用名义应力法对该圆角位置进行疲劳寿命分析。

3.1 确定各影响因素的系数

影响结构或机械疲劳寿命的因素主要有应力集中、尺寸、表面状态及载荷。

3.1.1 应力集中系数

转臂圆角处的理论应力集中系数KT计算公式[8]：

(1)

式中：σmax为转臂圆角处的最大弹性应力，即127.4 MPa；σ0为名义应力，参考图1所示裂纹的路径，利用有限元分析软件对刮料工况的静力计算结果进行后处理，得到转臂该路径的名义应力，35.3 MPa。

将σmax=127.4 MPa，σ0=35.3 MPa代入式(1)，得KT=3.6。

3.1.2 疲劳缺口系数

疲劳缺口系数Kf选用R.E.Peterson公式[8]计算，即:

(2)

式中：ρ为缺口根部半径，取15 mm；a为材料常数，查图1.8[8]，取0.4；KT=3.6；则Kf=3.5。

3.1.3 其他影响因素系数

根据文献[8]，尺寸系数ε值取1，表面状态系数β值取0.9，载荷的影响系数CL值取0.85。

3.2 修正S-N值

根据文献表40.3-3[7]，45号调质钢的疲劳寿命S-N值如表2所列。

表2 45号调质钢S-N值

将上述材料的S-N值修改成转臂结构的S-N值。综合考虑结构的疲劳强度影响因素，该转臂结构的应力按式(3)修正：

(3)

式中：S为修正前的应力。修正后转臂结构的S-N值如表3所列。

表3 转臂结构的S-N值

由试件的应力比r=-1，可知该试件的平均应力Sm0=0，而转臂的平均应力：

Sm=σmax/2 ，即Sm=63.68 MPa。由此，按Goodman直线模型公式(4)进一步作平均应力修正：

(4)

修正后的S-N值，即转臂结构的S-N值如表4所列。

表4 转臂结构的S-N值

3.3 疲劳计算

刮刀离心机的每个工作周期按通常5 min计算，每天24 h运行，每年运行300天，20年将经历172.8万次循环。依据线性疲劳累积损伤理论的Miner理论，基于转臂在刮料工况下的计算结果及修正后的S-N值如表4所列，利用ANSYS软件的Fatigue功能计算转臂的疲劳寿命耗用系数。转臂疲劳源处的最大等效应力经历172.8万次循环后的疲劳耗用系数为0.892<1，可知转臂使用20年不会发生疲劳破坏，该转臂的设计满足使用寿命要求。

4 结 论

(1) 为了模拟转臂真实的边界条件，建立了与之关联的螺钉与刮料斗的有限元模型，考虑了螺钉预紧力、转臂与刮料斗之间的摩擦力及支撑刮料斗的轴承约束，获得了转臂准确的静力计算结果。

(2) 静力分析计算结果确定了转臂易发生疲劳破坏的部位及该部位的应力集中系数，为疲劳分析提供了参考依据。

(3) 基于转臂材料的S-N数据，经过修正，获得了转臂结构的S-N数据，实现了复杂转臂结构的疲劳分析。