关于试验设备温度偏差校准结果不确定度分析评定
王静敏
(福建省计量科学研究院,福建 福州 350003)
温度测量设备是由两个部分组成的,第一部分是温度传感器,第二部分是用于鉴定温湿度的测量设备检查仪,该套装置具有相对应的温度校准值。保证环境试验装置处于一个稳定状态,工作空间各个测量点在规定时间内进行实测,所得的最高温度以及设定的温度存在上下的偏差,一种是温度高于设定值,记为温度上偏移,一种是温度低于设定值,记为温度下偏移。由此,展开记录分析。
1.温度数据处理
温度偏差测量模型:Δtmax=tmax-ts

式中:Δtmax-温度上偏差,℃;
Δtmin-温度下偏差,℃;
tmax-各测量点规定时间内测量的最高温度,℃;
tmin-各测量点规定时间内测量的最低温度,℃;
ts-温湿度试验设备设定温度,℃。
2.导致温度不确定原因分析
被测设备仪表可能存在重复读数的问题;
标准器分辨力引入的标准不确定度读数分量;
温度测量装置读数重复性引入的标准不确定度分量;
温度测量装置引入的标准不确定度u4,从标准仪器的校准证书中获得;
标准仪器修正值中所引入的标准不确定性分量;
标准器稳定性引入的标准不确定度分量。
3.不确定度分量问题分析
3.1 由tmax,tmin 引入的不确定度分析
对大气环境质量实验检测设备的显示平均值,可以作10次独立或多次重复的数据测量,从实验设备的数据显示仪上可以记录下每个显示器上各位置,同时读取10 次的数据显示值,记为td1,td2,…,td10,平均值数据标记格式为,其在40℃为校准点,记下每次测量10 组数据39.90、39.90、40.00、40.00、40.00、39.90、40.00、40.00、39.90、40.00,由于上偏差与下偏差温度不确定性数据来源及其统计数值不一致,因此本文只是以气体温度上的上下偏差为实际应用案例,进行了偏差不确定度的分析评价。
根据公式
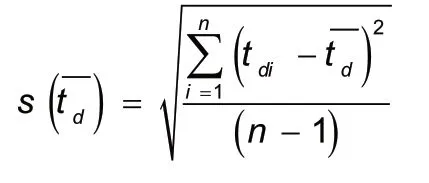
3.2 由标准仪器分辨力导致引入的非确定度分量分析
标准仪器在分辨率下的测量力引入的不确定度u2,标准仪器的区间分辨力长度范围大小为0.01℃,不大于确定的长度区间范围区间半宽0.005℃,服从均匀的区间分布,则根据该区间分辨力值的计算可得出可以引入一个标准器不大于确定的长度区间分量:

3.3 温度测量装置读数重复性u3
对于一台环境实验设备进行10次独立或多次重复的测量,从一台标准仪的显示器上判断每个设备分别读取10 次的显示数据值,记为 ti1,ti2,…,ti10,量程为-80~0℃,以-50℃为例,其测量10 次:-50.12、-50.15、-50.23、-50.19、-50.34、-50.26、-50.18、-50.15、-50.08、-50.01。
根据公式

则由10 次独立或非一次重复标准测量所直接引入的标准测量不确定性值的分量值为u3=s()=0.09℃。
量程为0~100℃,以40℃为例,其测量10 次:39.95、39.95、39.97、39.91、39.98、39.92、39.95、39.98、39.93、39.89,计算所要求的实验算术误差平均值为一个实验标准差值,即s()=0.03℃。则由10 次独立或非标准稳定性独立重复温度测量引入所对应引入的一个标准独立不确定性重复分量值为u3=s()=0.03℃。
量程为100~300 ℃,以200 ℃为例,其测量10 次:199.89、199.92、199.93、199.96、199.94、199.95、199.98、199.95、199.96、199.92,计算所需求的实验算术误差平均值为一个实验标准差值即s()=0.03℃。则由10 次独立或非标准稳定性独立重复温度测量所对应引入的一个标准独立不确定性重复分量值为u3=s()=0.03℃。
则由ti 引入的不确定度如表1 所示:

表1 ti 不确定度数据表
3.4 温度测量设备引入的标准不确定度u4
从标准仪器的校准证书中获得不确定度如表2 所示:

表2 u4 不确定度数据表
3.5 标准器修正值所引入的标准不确定性分量u5
标准器的确定温度分量校验值经过修正后,如果取得的不大于确定的温度值为U=0.04℃,k=2,则根据一个标准器的确定温度分量校验值可以引人一个标准不大于确定的温度的一个分量:u5=U/K=0.04/2=0.02℃
3.6 标准器稳定性引入的标准不确定度分量u6
本统计方法对于一个标准器中进行相邻两次校准,改变时间的平均温度进行修正,平均值最大温度改变0.10℃,按均匀温度分布。由此我们可以重新引入一个标准不确定改变程度中的分量:u6=0.10/=0.06℃
4.关于不确定度总结分析
4.1 标准不确定度分量一览表

表3 标准不确定度分量一览表
4.2 合成标准不确定度

表4 合成标准不确定度分析表
4.3 计算扩展不确定度
取包含因子k=2,计算扩展不确定度如表5 所示:

表5 计算扩展不确定度分析表
5.测量不确定度的报告与表示
温度试验设备温度偏差校准结果不确定的扩展不确定度为测量范围-80~0℃:U =0.26℃,k=2;测量范围0~100℃:U=0.16℃,k=2;测量范围100~300℃:U =0.20℃,k=2。

