基于全卷积金字塔残差网络的能谱CT图像降噪研究

任学智， 何 鹏,*， 龙邹荣， 郭晓东， 安 康， 吕小杰， 魏 彪,， 冯 鹏,*

1. 重庆大学光电技术及系统教育部重点实验室， 重庆 400044 2. 重庆大学工业CT无损检测教育部工程研究中心， 重庆 400044

引 言

传统CT(computed tomography)通过能量积分式探测器将不同能量的X射线光子整合接收， 反映了X射线的平均衰减特性[1]， 导致图像中密度相近物质的成像对比度差异小， 难以区分微小的组织结构[2]。 基于光子计数探测器的能谱CT(spectral CT)通过探测器设定能量选通阈值能够采集不同能量范围的X射线光子， 可以有效抑制射线束硬化伪影、 提高密度相近物质的成像对比度[3]。 而能谱CT在特定能量范围内探测的X射线光子数有限， 致使投影数据中含有较多的量子噪声， 重建的能谱CT图像信噪比较低。

在能谱CT图像降噪研究方面， 现多采用迭代重建算法对投影数据进行重建以抑制噪声。 例如Clark等[4]结合图像的稀疏特性和能谱CT图像相关性以构建重建目标函数， 提高了能谱CT图像重建效果。 Rigie和Riviere等[5]提出了一种基于矢量全变分(TV)的能谱CT重建算法。 上述图像重建降噪算法可以较好的抑制能谱CT重建图像中的噪声， 但算法复杂度较高、 计算时间较长。 近年来， 深度学习在CT图像降噪领域中得到了广泛应用[6-7]。 神经网络可以直接提取图像中噪声的特征信息， 进而通过与标准图像作对比抑制训练图像中的噪声。 例如Chen等[8]研究一种CT图像去噪的浅层卷积神经网络模型， 基于该网络提出了残差编码器-解码器卷积神经网络， 并使用反卷积网络和快捷连接以增强网络降噪性能。

本文提出一种基于全卷积金字塔残差网络(fully convolutional pyramidal residual network， FCPRN)的能谱CT图像降噪方法。 利用能谱CT获取的图像数据训练全卷积金字塔残差网络， 训练后的网络模型可以有效的抑制能谱CT图像中的噪声。 与常用的CT图像降噪网络相比， 本文提出的全卷积金字塔残差网络具有更好的图像降噪效果。

1 基于深度学习的能谱CT图像降噪方法

1.1 方法原理

为开展基于深度学习的能谱CT图像降噪方法研究， 我们搭建了能谱CT系统并在多个能量范围扫描一个小鼠样本， 分别用Feldkamp(FDK)算法[9]和SplitBregman算法[10]重建不同能量范围的CT图像。 FDK算法重建效率高， 但重建效果差， 重建图像中含有较多的噪声。 Split Bregman重建算法相对复杂， 但重建效果好， 能够有效抑制重建图像中的噪声。 两种算法重建的图像对比， 其结构信息大致相同， 主要区别在于噪声水平不同。 将Split Bregman算法重建图像作为标签数据x， 不同类型的噪声的集合设为v， FDK算法重建图像作为训练数据y， 训练数据和标签数据相对应， 则有y=x+v。 在训练神经网络时， 我们设定残差学习公式训练残差映射R(y)≈v， 最后通过x=y-R(y)得到抑制噪声后的图像。 期望残差图像与输入估计残差图像之间的均方误差为

式(1)中， N为图像数量， xi和yi代表图像中的像素值。 将均方误差作为损失函数， 使用数据集训练FCPRN。 训练模型能提取不同能量范围的CT图像噪声， 利用输入图像减去噪声得到输出图像， 即降噪后的图像。 在对FDK算法重建的能谱CT图像降噪时， 调用该网络模型可直接对图像进行校正， 能够有效的提高能谱CT图像的重建质量和重建效率。

1.2 全卷积金字塔残差网络

基于FCPRN实现降噪的， 该网络由全卷积网络(fullyconvolutionalnetwork)[11]和金字塔残差网络(pyramidalresidualnetwork)[12]组合而成， 网络结构示意图如图1所示， 主要分为上采样路径和下采样路径两部分。 在下采样路径中， 使用3×3卷积(convolution：Conv)提取图像的特征信息， 后利用多个金字塔残差模块(pyramidresidualblocks，PR-blocks)提取图像的特征信息，PR-blocks主要包括批量归一化(batchnormalization，BN)， 修正线性单元(rectifiedlinearunit，ReLU)， 3×3Conv和零填充(zeropadding)等结构。 零填充可保证输出图像的尺寸与输入图像一致。PR-blocks组输出的图像维度可以表示为

图1 FCPRN结构图Fig.1 FCPRN structure

式(2)中， Din和Dk分别代表第k层PR-blocks的输入图像维度和输出图像维度。 j代表PR-blocks组中残差模块的数量，FCPRN中每个金字塔残差模块组中包含4个金字塔残差模块。PR-blocks组中特征图的维度是按照固定值n增长的， 有利于防止特征维度爆炸， 便于设计更加深层的网络结构。 下采样路径使用下采样模块(transitiondown，TD)降低特征图的分辨率， 下采样路径共包含四个金字塔残差模块组和4个下采样模块。 在下采样中， 使用了池化层提取图像的特征， 为了减少信息损失， 本文使用跳跃连接(skipconnection)将下采样模块和上采样模块(transitionup，TU)连接在一起， 将浅层网络的图像信息传送到深层网络中。 与此同时， 在上采样路径和下采样路径之间使用瓶颈结构[13](bottleneck)以避免维度爆炸和梯度消失问题。

在上采样路径中， 使用转置卷积(transposition convolution)恢复图像特征图。 然后使用多个PR-blocks降低特征图的维度， 上采样路径共有四个金字塔残差组和四个上采样模块， 最后使用3×3 Conv将图像的特征维度恢复到与输入图像相同。 在实验中， 输出图像即为预测的噪声图像， 使用输入图像减输出图像得到噪声抑制后的图像， 由此， 可以训练出提取图像噪声信息的神经网络模型， 我们设计的FCPRN结构参数如表1所示。

表1 FCPRN的结构参数表Table 1 The structure and parameters of FCPRN

FCPRN使用跳跃连接将浅层网络中的图像信息传递到深层网络中， 能够有效的减少图像信息损失， 结合全卷积可以精确地识别图像中的每个像素， 有助于提取图像特征信息。 FCPRN依据残差学习的方法， 将图像中的特征信息——噪声作为学习对象， 可以提高神经网络的学习效率。

2 实验及结果讨论

2.1 数据采集与处理

实验数据是通过自主搭建的能谱CT获取的， 该系统实物图如图2所示。 探测器为DECTRIS公司生产的SANTIS 0804光子计数探测器， 有效探测面积为1 024×256像素尺寸为150 μm。 检测对象为一个小鼠样本， 体长约10 cm， 体重在150～180 g之间， 使用氨基甲酸乙酯麻醉后放置在塑料瓶中进行扫描。 数据采集系统的几何参数是根据小鼠的规格进行设置的， 源到探测器的距离为350 mm， 源到探测物体的距离为210 mm， 系统的管电压为90 kVp， 管电流为200 μA， 实验共设置25～90,30～90,35～90,40～90,45～90和50～90 keV六个能量范围进行数据采集， 每个能量范围内360°等角度扫描获取250组投影。

图2 能谱CT数据采集实物图Fig.2 Spectral CT system based on photon-counting detector

获取能谱CT投影数据后， 首先使用FDK算法对不同能量范围内的数据进行三维重建， 并将其作为训练数据， 共重建了六个能量段的小鼠图像， 某一切片的训练数据如图3。 然后使用Split-Bregman算法[14]进行三维重建， 并作为标签数据。 标签数据和训练数据层层对应， 同一切片标签数据和训练数据的主要区别在于图像噪声水平不同。 与训练数据对应的某一切片的在不同能量范围内的标签数据如图4所示。

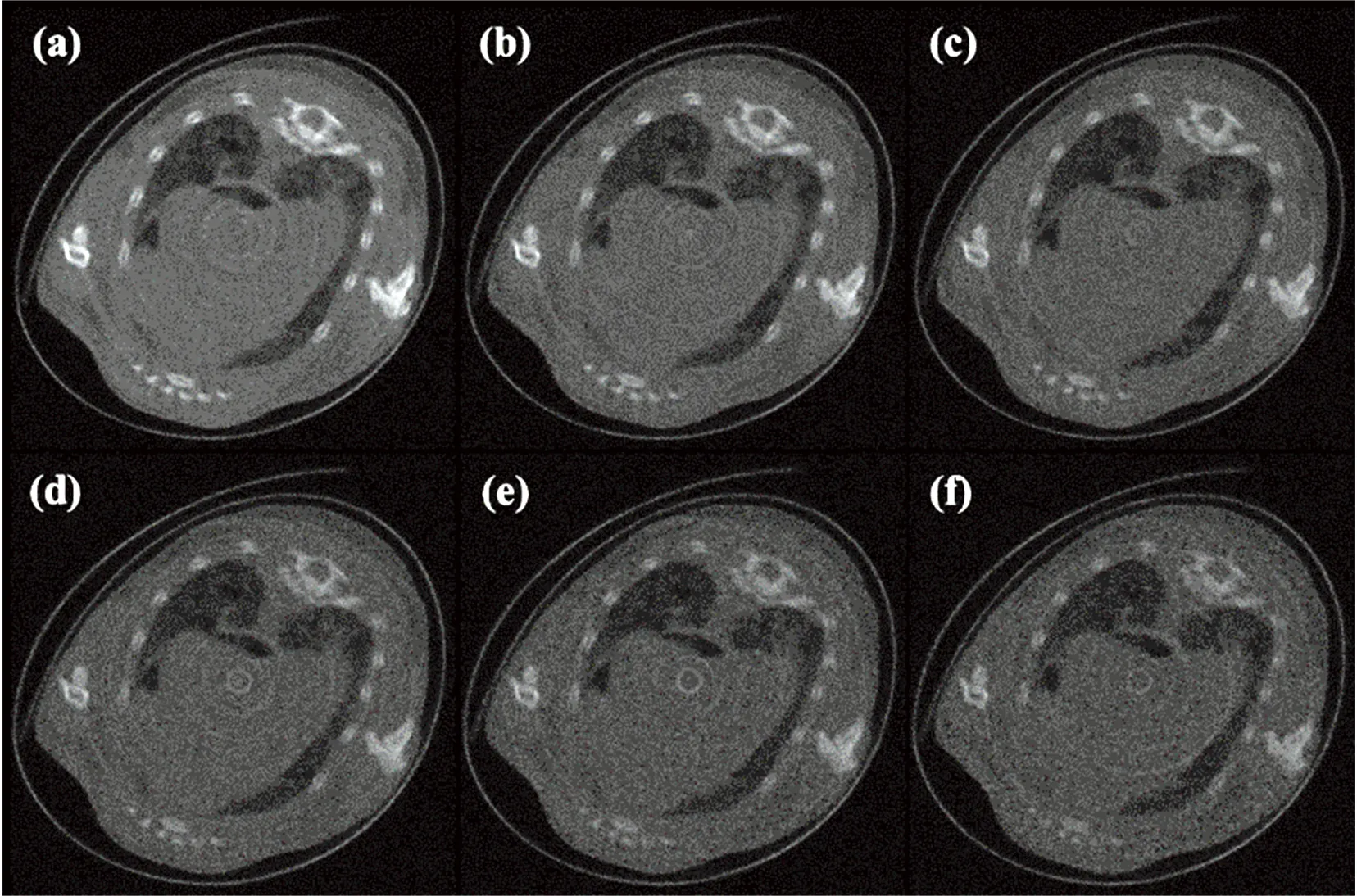
图3 六个能量段某一切面的能谱CT图像训练数据图

图4 六个能量段某一切面能谱CT图像标签数据图

在每个能量段重建256个切面图像， 因此六个能量段共有1 536个切面图像， 为了使FDK算法重建的图像与Split-Bregman算法重建的图像相匹配， 实验将三维数据等间隔划分为256个切片图像。 此外， 为了提高训练模型的泛化能力， 将这些能谱CT图像按照1∶1∶5的比例随机划分为验证集、 测试集和训练集。

2.2 实验结果

我们实验分析并对比了在低剂量CT降噪中表现较好的REDCNN[8]和广泛用于图像降噪的DNCNN[15]。 DNCNN主要包含三类网络层： 第一类即第一层包含3×3×nConv和ReLu； 第二类包括含3×3 Conv、 BN以及ReLu， 此类作为中间层， 共有17层； 第三类即最后一层包含3×3 Conv和ReLu。 其中每一层都包含zero padding， 使得每一层的输入、 输出尺寸保持一致。 REDCNN使用卷积层进行编码， 使用反卷积层进行解码， 并借助跳跃结构进行连接， 减少信息损耗。 在对三种网络进行训练时， 所使用的数据和训练条件完全相同， 其中DNCNN和FCPRN使用残差学习的方式进行训练， 网络学习图像中噪声的特征信息， 而REDCNN学习整个图像特征信息， 由此最大限度的发挥三种网络的性能。 网络训练的初始学习率为0.001， 每训练一次学习效率变为之前的95%， 损失函数为均方误差(mean squared error， MSE)， 使用Adam (adaptive moment estimation)算法进行优化。 训练模型所使用的计算机软硬件配置如下： TITAN XP显卡， 显存为12G， Intel i7-8700KCPU， 16G计算机内存， Ubuntu16.04系统， 神经网络框架及版本为Pythorch 0.4.0。 训练结束后得到的网络模型可以对FDK重建算法得出的数据进行降噪。 我们选择了25～90,35～90和45～90 keV三个能量段的某一切面进行对比， 如图5所示。 可以看出， 由DNCNN和REDCNN模型输出的能谱CT图像的噪声相对明显， FCPRN模型对图像中噪声的抑制效果较好， 由此可以推断本文提出的FCPRN有较好的降噪性能。 为了更好地展示降噪细节， 我们放大显示降噪后图像的部分区域， 如图6所示， 可以看出， FCPRN的降噪性能优于DNCNN和REDCNN， FCPRN输出图像中不同组织之间的对比度相对较好， 信噪比较高。

图5 三种网络对不同能量范围能谱CT图像降噪效果图

图6 三种网络对不同能量范围能谱CT图像降噪效果放大示意图第一列为训练图像， 第二列为训练图像选定区域放大图， 第三列至第五列为DNCNN， REDCNN和FCPRN的降噪图像选定区域放大图；第一行至第三行对应25～90,35～90和45～90 keV三个能量范围的图像Fig.6 Details of denoising based on DNCNN， REDCNN and FCPRN in the three energy bins (25～90, 35～90 and 45～90 keV)

为了量化不同网络的降噪性能， 此处计算测试集的输出图像与标签图像之间的相似性参数如均方根误差(root mean squared error， RMSE)， 峰值信噪比 (peak signal to noise ratio， PSNR)和结构相似度(structural similarity， SSIM)进行对比。 训练模型的输出图像与标签图像的RMSE可以表示为

第一列为训练图像， 第二列至第四列为DNCNN、 REDCNN和FCPRN的降噪结果； 第一行至第三行为25～90,35～90和45～90 keV三个能量范围的图像

(RMSE(x,y))2=MSE(x,y)=

式(3)中， x和y代表两幅图像， m和n代表图像的边界尺寸，MSE代表均方误差。

假设MAXI是图像中的最大像素值， 则网络模型的输出图像与标签图像之间的PSNR可以表示为

网络模型输出图像和标签图像的SSIM可以表示为

式(5)中， μ， σ和σxy分别代表图像的均值， 方差以及协方差， c1=(k1L)2和c2=(k2L)2是两个用于避免计算错误的常数， L是像素值的变化范围。 具体结果如表2所示， 表中所列参数值为测试集中不同能量段所有图像的相似性参数平均值， 可以较好的反映模型的降噪效果。 可知FCPRN输出图像与标签图像之间的PSNR值和SSIM值高于其他网络， RMSE值低于其他网络， 这表明FCPRN的降噪性能高于DNCNN和REDCNN。

表2 不同网络的去噪结果量化示意表Table 2 Quantitative results of different networks

3 结 论

为抑制能谱CT图像中的噪声， 本文提出了一种基于全卷积金字塔残差网络(FCPRN)的能谱CT图像降噪方法， 并实验验证了方法的可行性。 由文中表2可知， FCPRN能够有效的抑制能谱CT图像中的噪声， 但其在不同能量段内的降噪效果不同， 这与标签数据的制作水平以及窄能段内能谱CT图像中的噪声水平较高有关， 本文将基于Split-Bregman算法重建的图像作为标签数据， 但其中的噪声并没有被完全去除， 训练模型输出的图像只能尽可能的逼近标签而不可能超越标签， 我们会在后续的工作中使用含有加性高斯噪声的仿真图像和真实图像联合训练神经网络以提高模型的降噪能力。 此外， 因光子计数探测器探测单元一致性差等因素的影响， 致使不同能量段内的重建能谱CT图像出现了环形伪影。 在后续的研究工作中， 我们会对环形伪影去除做进一步研究， 验证能否使用神经网络同时抑制能谱CT图像中的噪声和伪影。

本文提出了一种基于深度学习的能谱CT降噪方法， 实验结果表明该方法可以有效的抑制不同能量段内能谱CT图像中的噪声， 使用的全卷积金字塔残差网络的降噪性能也优于文中提到的常用降噪网络DNCNN和REDCNN。