基于目标级联分析法的分布式主体可交易能源模型

姚 璐，赵维兴，李舒佳，肖孝天，谢 敏，宋 尧

（1. 贵州电网有限责任公司贵安供电局，贵州 贵阳 550003；2. 贵州电网有限责任公司电力调度控制中心，贵州 贵阳 550003；3. 华南理工大学 电力学院，广东 广州 510641）

0 引言

近年来，用户侧分布式能源数量与规模增长迅速［1］。电力市场化改革方兴未艾，5G 等先进通信、控制技术从研究成果迅速转化为生产力［2］。生产型消费者作为市场主体逐渐兴起，使得电力系统需求侧呈现多分布式主体的局面。考虑到分布式能源的随机性及现有的电网网架无法支撑用户侧大规模分布式能源的接入，加强分布式主体之间的能量互动、促进各主体内部能量实时平衡极具前景。为设计合理有效的经济激励机制，可交易能源概念应时而生。其最初的定义为“一套通过经济手段和控制手段，以价值为参数调节系统全局供需动态平衡的电力系统运行机制”。

可交易能源是一个结合经济交易与电力系统优化运行的综合概念，国内外对于结合经济交易与电力系统优化运行已有一定的研究基础。文献［3］以经济交易为主，从用户、微电网、虚拟电厂等不同电力系统主体介绍3 种分布式交易模型。文献［4-5］介绍了面向分布式能源主体的可交易能源系统，并从特征意义、体系设计及关键技术等方面进行了探讨。在建立交易与优化运行模型方面，文献［6］建立了一种基于讨价还价博弈的分布式能源合作收益分配模型，在约束条件中考虑功率平衡和各设备运行约束。文献［7］提出了一种新的交易式能源控制（TEC）实现分布式主体的能源交易。文献［8］建立了社区能源管理的联盟博弈模型，模型中考虑储能、可控负荷的建模和运行约束。文献［9］基于对偶次梯度法建立产销一体化分布式主体交易模型，模型中考虑优化运行相关约束。文献［10］采用拉格朗日分解法实现了分布式能源优化运行的交易式控制。为了实现交易网络信息交换的去中心化，文献［11］建立了互联微电网交易模型，通过纳什议价鼓励积极地参与能源交易，并通过引入交替方向乘子法（ADMM）解决纳什议价需要较全面的信息的缺点。文献［12］设计了基于ADMM 分布式优化的能源定价方法，在获得交易电价的同时实现了分布式能源优化运行。文献［9］、文献［10］和文献［11-15］分别采用了对偶次梯度法、拉格朗日分解法、ADMM 实现了交易网络信息交换的去中心化，其中文献［13］为ADMM提供经济学视角。

在实现经济交易问题与电力系统优化运行结合方面，相较于ADMM、对偶次梯度等方法，目标级联分析法（ATC）理论不局限于拉格朗日形式，还可以采用指数形式等多种形式，具有更为灵活多变的优点［16-18］。当前ATC 理论在电力系统领域应用方面已有相关研究。文献［19-21］将ATC 用于求解分散系统调度问题，但是在交互性方面并未实现所有主体之间的相互联系同时并未体现价格影响优化运行。文献［22］将ATC 用于完全竞争发电市场，将问题分解成发电机节点报价以及系统运营商出清2 个阶段，但仅考虑了ATC 理论在加速迭代收敛方面的优势，并未考虑ATC 灵活多变的特点对市场化结合运行出力计划问题的影响。

本文在实现分布式主体物理元素建模的基础上建立了面向分布式主体的可交易能源模型，模型分为优化运行与价格更新两部分。提出以ATC 理论实现产销一体化分布式主体优化运行模型与经济交易问题的结合。ATC理论的灵活性作用于本文提出的可交易能源模型具有分布式主体间的交易形式更灵活、形成的分布式主体间利益分配更多样的特点。

1 分布式主体的可交易能源机制

分布式主体可以是储能、分布式能源、灵活性负荷等多种资源的聚合体。广义的可交易能源机制涵盖了各类具有价值响应的电力交易形式［4］。在本文的可交易能源机制下，各主体根据最新的价格信号自行进行优化，并更新交易电价。各分布式主体之间进行点对点信息交换，形成去中心化交易网络，如图1所示。

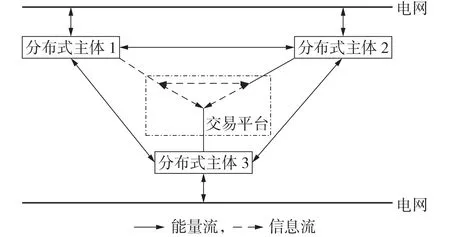
图1 可交易能源机制示意图Fig.1 Schematic diagram of transactive energy mechanism

2 分布式主体的物理元件建模

分布式主体，其内部通常包含燃气轮机、电锅炉、制冷机、温控负荷、储热装置、电动汽车等物理元件和设备，从而实现电-热-冷多种能源形式的互联。各物理元件模型具体如下。

2.1 燃气轮机

1）燃气轮机供电。

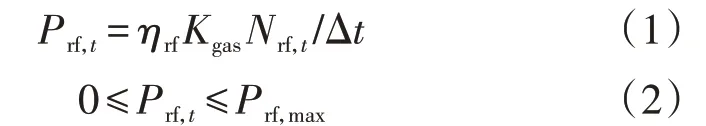
式中：Prf，t为t时刻燃气轮机发电功率；ηrf为燃气轮机发电效率；Kgas为天然气的燃料热值；Nrf，t为t时刻燃气轮机在单位时间内消耗的燃料量；Δt为时间间隔；Prf，max为燃气轮机最大发电功率。

2）燃气轮机供电供热。

当燃气轮机采用供电供热模式时，同样满足式（1）和式（2），但发电效率有所下降，此外增加供热约束如式（3）—（5）所示。

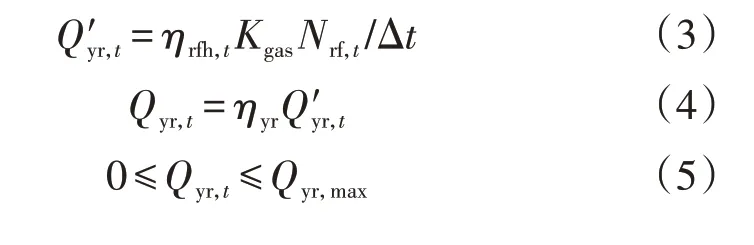
式中：Q′yr，t为t时刻燃气轮机输出的热功率；ηrfh，t为t时刻燃气燃烧时的烟气余热占比；Qyr，t为t时刻实际利用余热功率；ηyr为余热锅炉的效率；Qyr，max为燃气轮机输出的最大热功率。

2.2 电锅炉

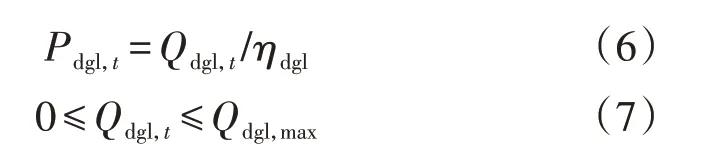
式中：Pdgl，t为t时刻电锅炉消耗的电功率；Qdgl，t为t时刻电锅炉供热功率；Qdgl，max为电锅炉最大供热功率。

2.3 制冷机

1）电制冷机。

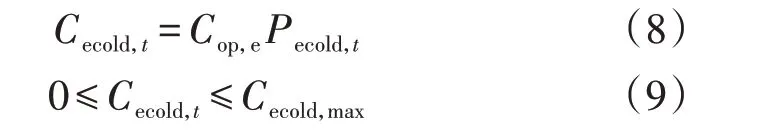
式中：Cecold，t为t时刻电制冷机制冷功率；Cop，e为电制冷机的能效比；Pecold，t为t时刻电制冷机消耗的电功率；Cecold，max为电制冷机的最大制冷功率。

2）吸收式制冷机。

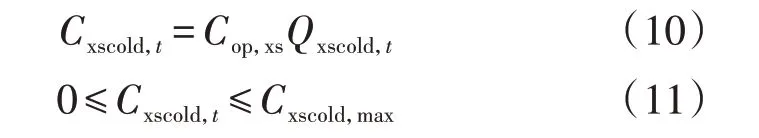
式中：Cxscold，t为t时刻吸收式制冷机的制冷功率；Cop，xs为吸收式制冷机的能效比；Qxscold，t为t时刻吸收式制冷机消耗的热功率；Cxscold，max为吸收式制冷机的最大制冷功率。

3）空调负荷。

2.4 蓄能装置

通过可行域定界［9］对存在状态转换的蓄能装置进行线性化建模。

1）蓄热装置。

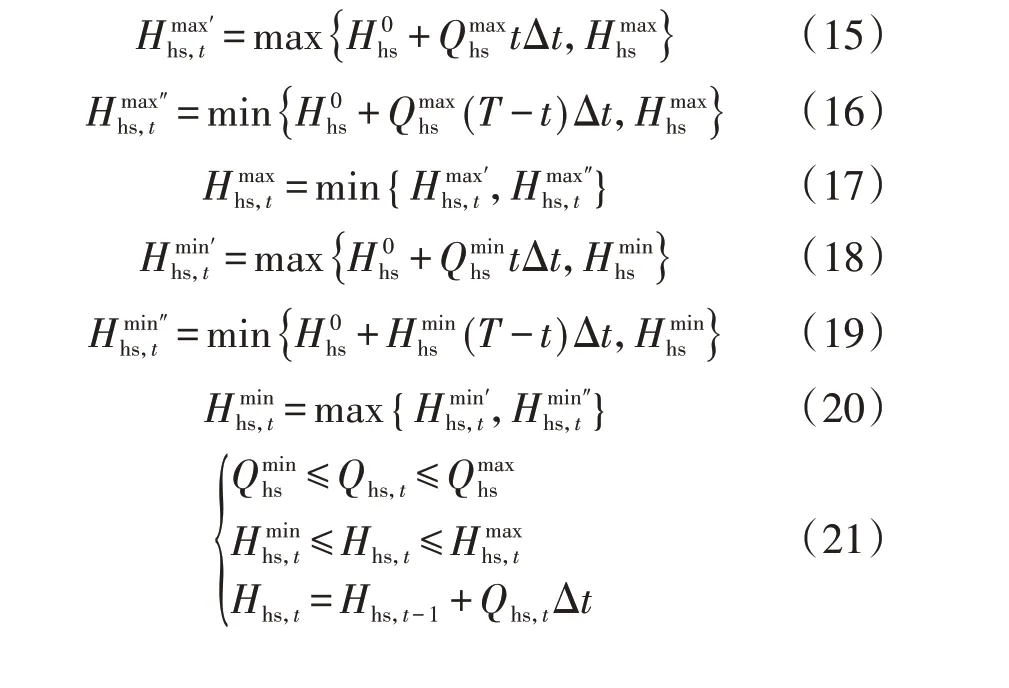
含有上述所有物理元件的分布式主体内部能量流动关系可用图2来描述。

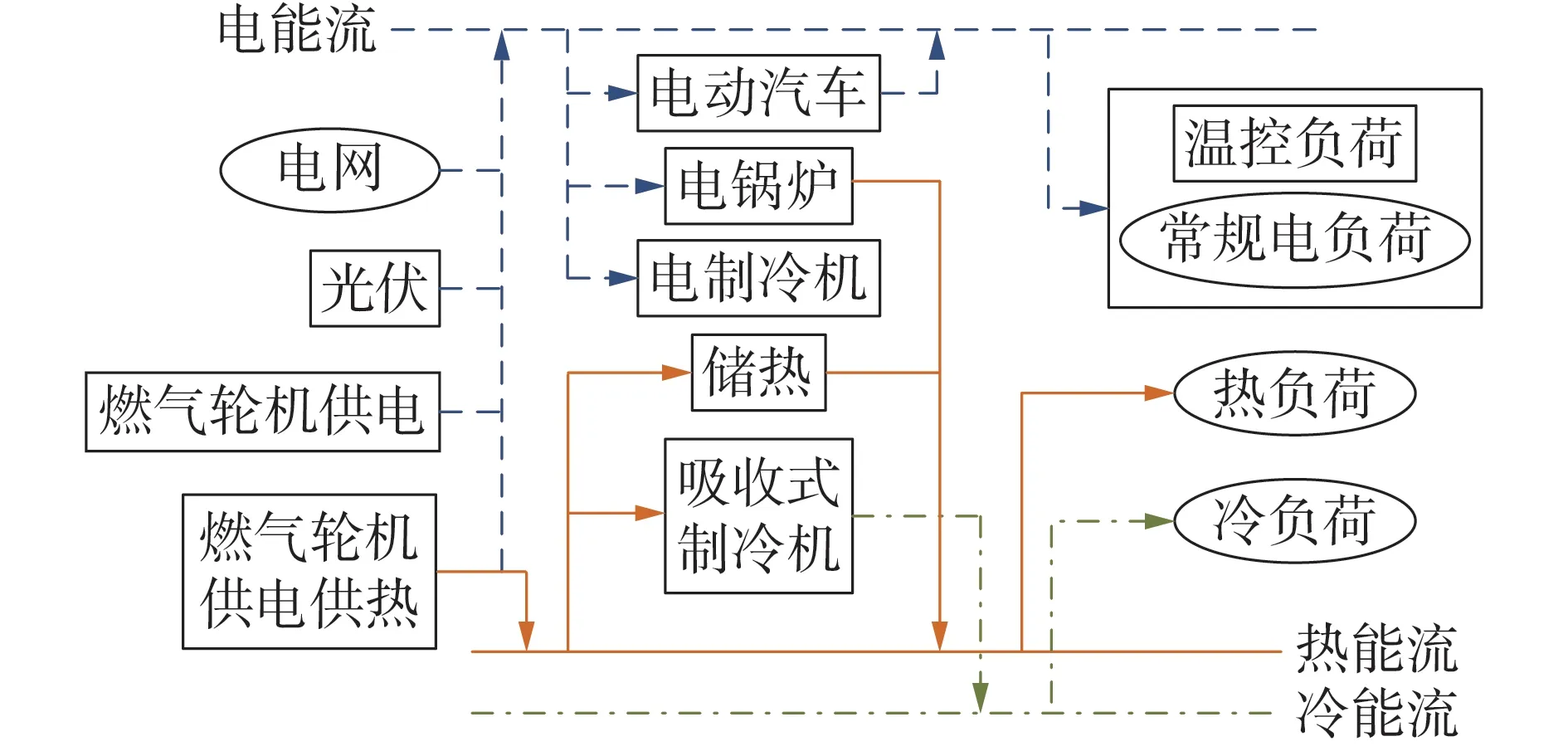
图2 分布式主体内部能量流动关系Fig.2 Energy flow relationship within distributed agents

3 基于ATC理论的分布式交易建模

3.1 ATC基本理论

ATC 理论由Kim 等人提出，是将复杂系统划分成2 层或多层子主体进行分布式求解的多学科设计优化理论。典型的ATC 结构如图3 所示。图中，O1为父代主体；S1，1—S1，n为子一代主体；S2，1—S2，m为子二代主体，其中S2，1—S2，j的父代主体为S1，1，S2，k—S2，m的父代主体为S1，n。每个主体可以有多个子代主体，但只有1个父代主体。

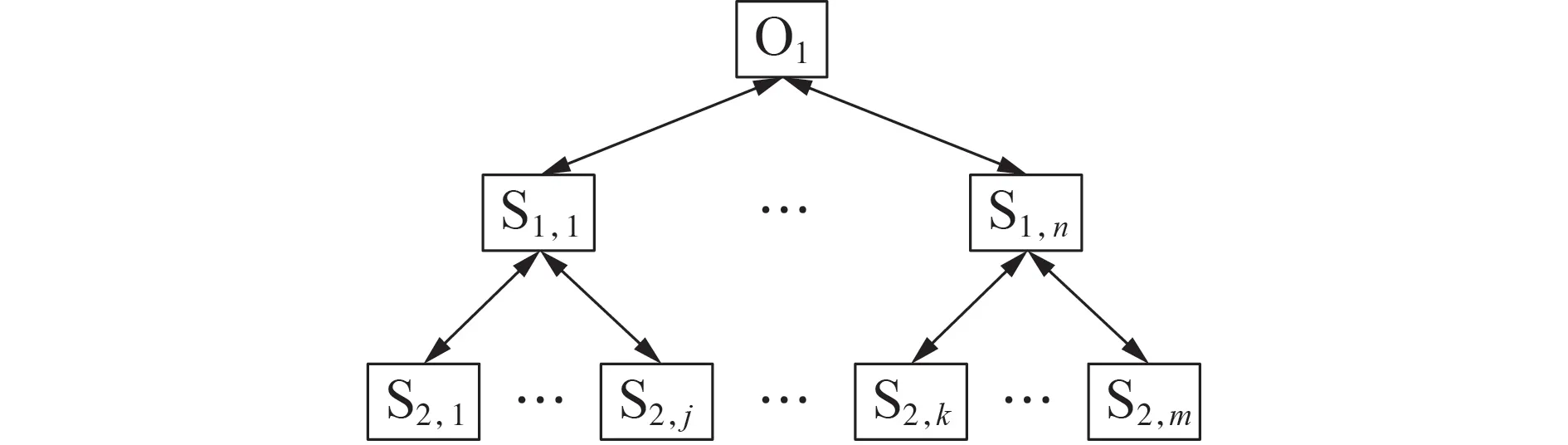
图3 ATC理论结构Fig.3 Structure of ATC theory

在运用ATC 理论进行分布式求解过程中，各层主体可以自行设定优化模型，各层主体优化模型中与其他层共同含有的变量为协同变量。如图3 所示的ATC 理论结构中，子一代主体接收来自父代主体和子二代主体发送的协同变量，并将其作为常量参与优化，优化后将自身优化所得的协同变量发送给父代及子代主体，父代及子代主体接收后同样将其作为常量加入自身目标进行优化。目标函数中这一组成部分称为罚函数部分，常见的罚函数形式有拉格朗日形式、增广拉格朗日形式、二阶对角形式、指数形式等。

根据上述ATC 理论实现协同的方式，当将其运用于本文所提可交易能源机制时，存在的优势在于罚函数形式多样且有进一步扩展的空间，为分布式主体间利益分配提供多样性。

3.2 基于ATC理论的可交易能源模型

根据图3 所示的ATC 理论结构，基于ATC 理论的可交易能源模式的上层目标函数为所有分布式主体的总体购电费用F最小：

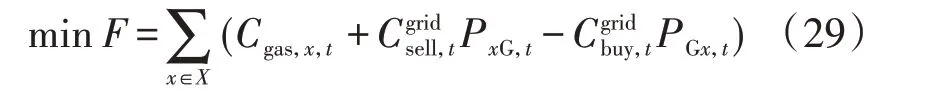
式中：x为分布式主体对象；X为所有分布式主体的集合；Cgas，x，t为t时刻分布式主体x的燃料成本，若无燃气设备，此项为0为t时刻电网的售电价格；PxG，t为t时刻电网向分布式主体x的售电功率为t时刻分布式主体x向电网的售电价格；PGx，t为t时刻分布式主体x向电网的售电功率。

显然，上层目标函数中未包含各分布式主体之间的电能交易相关成本，无需集中处理所有分布式主体的购售电功率以及交易价格，实现了交易网络的去中心化。

各主体以其自身购电费用最小为目标，则优化目标F′x为：

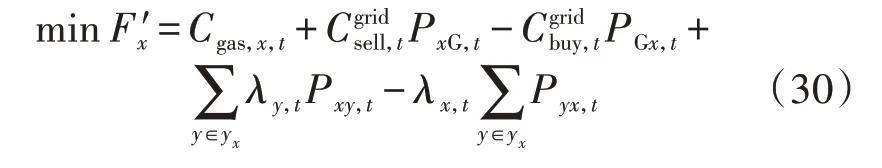
式中：yx为除分布式主体x外的本地售电主体集合；λy，t为t时刻主体y的售电价格；λx，t为t时刻主体x的售电价格；Pxy，t和Pyx，t分别为t时刻主体x向主体y的购电功率和主体x向主体y的售电功率。

根据3.1 节，基于ATC 理论的各分布式主体的目标函数中因补充与接收到的协调变量常量相关的罚函数，故修改后的目标函数如下：

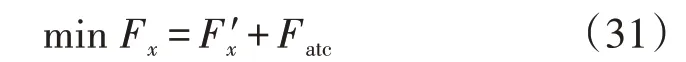
式中：Fx为修改后的优化目标；Fatc为协调变量常量引入目标后的附加罚函数部分，根据罚函数的形式具有不同的表达形式。

在协调过程中，当自身优化所得协调变量与接收到的常量偏差过大，下一次协调时Fatc将增大，优化结果向协调一致方向靠拢；当偏差较小时，优化结果向经济目标靠拢。因此，不同罚函数Fatc及对应更新方式将影响基于ATC 理论的目标函数形式，进而影响本文所提可交易能源模式最终形成的全时刻价格以及各主体利益分配结果，下面选择2 种常见的罚函数形式进行建模。

1）罚函数形式1。

基于ATC 理论，采用二阶对角形式的罚函数，则有：

该形式的特点是目标函数罚函数部分受2 个协调乘子的影响，其具体影响将与初值以及乘子更新方式相关，采用二阶对角形式罚函数的乘子更新方式为：

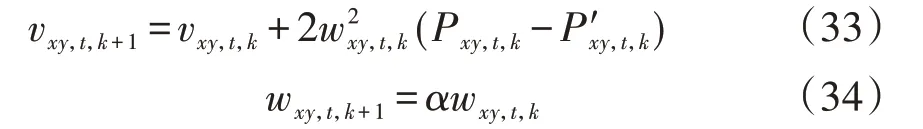
式中：下标k表示第k次迭代；为保证收敛，α一般为大于等于1的数。

当选取一定的乘子初值时，在协调变量不一致的情况下，二次项wxy，t随着迭代次数的增大而增大，使得协调部分占目标函数比重增大，进而通过损失一定的经济性促进协调变量趋向一致。因此采用二阶对角形式乘子更新的主体的合作策略随着通信次数的增多，将不断地趋向于达成交易。

2）罚函数形式2。

基于ATC 理论，采用拉格朗日对偶形式的罚函数，则有：

该形式的特点是罚函数二次项与一次项乘子系数变化趋势一致，乘子将与初值以及乘子更新方式相关，本文采用的拉格朗日对偶罚函数的乘子更新方式为：

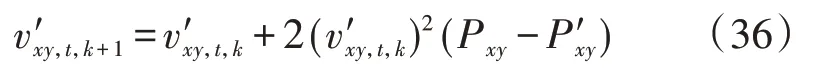
若乘子的初值一定，在协调变量不一致的情况下，当第k次迭代中主体x向y供给的功率大于y的需求时，v′xy，t，k+1将大于v′xy，t，k，使得协调部分占目标函数比重增大，进而通过损失一定的经济性促进协调变量趋向一致；当第k次迭代中主体x向y供给的功率小于y的需求时，v′xy，t，k+1将小于v′xy，t，k，使得协调部分占目标函数比重减小，进而使得主体x转向考虑经济性目标。综上可知，这种乘子更新方式背景下的主体交易电价能够较好地跟随电网交易电价。

可见，上述2 种目标函数形式可以在一定程度上刻画市场主体的协调行为，除此之外，ATC的罚函数还有其他多种类型［16-18］，通过更高效的协调方式，ATC 理论可以实现市场主体行为更为精细、灵活的刻画。

对于分布式主体，在系统运行以及市场行为方面，存在主体功率平衡约束、购售电功率一致约束与电网交互功率约束，具体如下：

3.3 考虑价格调节优化运行的收敛判据

除满足式（42）、（43）所示ATC 收敛条件［23］外，为体现2 次迭代前后交易电价对优化运行结果的控制意义，需要满足收敛条件式（44）。

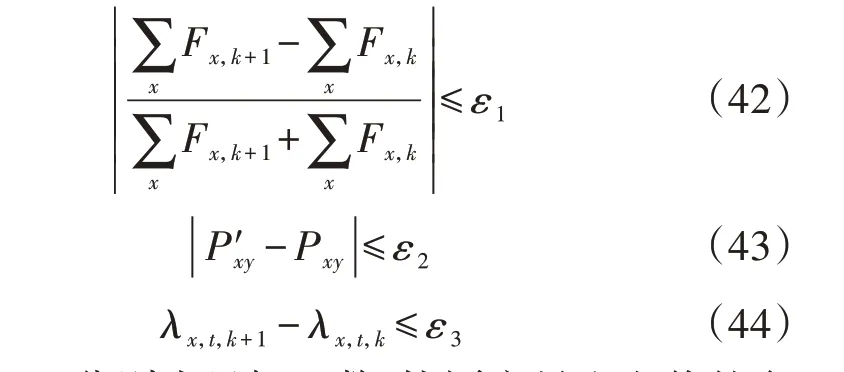
式中：ε1—ε3分别为目标函数、协同变量和电价的允许容差。

当不满足收敛条件时，采用式（33）和式（34）或式（36）进行乘子更新，同时采用式（45）进行交易电价更新，并用新的交易电价参与新一轮迭代的优化运行。

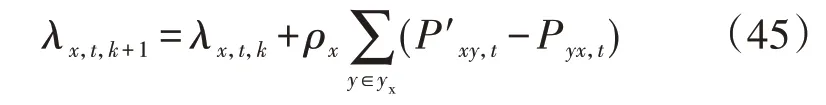
式中：ρx为主体x对电价的敏感度因子。由式（45）可见，式（43）与式（44）的收敛方向应该是一致的。

4 算例分析

设分布式主体1，以某实际智慧小区为原型，含联合循环燃气轮机、电动汽车、空调负荷和光伏，且固定负荷较少；分布式主体2，以某实际行政办公区为原型，含电动汽车、空调负荷且具有基数较大的固定负荷，但无分布式能源；分布式主体3，以某工业园区为原型，含燃气轮机、电锅炉、电制冷机、余热锅炉、蓄热装置和光伏，且存在能源信息中心，具备多能调控的能力。各主体对电价的敏感度因子均取5×10-3。电动汽车参数见附录A 表A1，设备参数见附录A 表A2，室外温度曲线、光伏出力预测曲线、负荷预测曲线分别见附录B 图B1—B3，电网购、售电价见附录B图B4，整体信息参考图1所示的结构。

4.1 优化结果

将一天等分为24 个时段，2 种罚函数形式下的优化结果分别见附录C 图C1 和图C2。考虑到2 种罚函数形式下的优化结果的区别不明显，下面仅对罚函数形式1下的优化结果进行分析。

由图C1（a）可知，住宅园区灵活性资源丰富且具有分布式能源，但自身负荷较少。燃气轮机出力集中在06:00 之后。住宅区过剩的功率供给一部分即时销往其他主体和电网，另一部分通过电动汽车充放电实现电能时间价值转移以获取更大规模的利益。向其他主体供电以及向电网供电的功率在12:00—14:00时段达到并维持较大值。室内温度有一定的控制范围，除04:00 外，空调负荷集中于电价午高峰后出现。

由图C1（b）可知，市政工作区无分布式能源，含灵活性负荷以及较大基数固定负荷，电能供小于求。其主要功率来源为其他主体和电网送电。电动汽车充放电行为集中在09:00—20:00 时段，在电价午高峰期放电、其余时段充电，在负荷低谷期向其他主体供电。

由图C1（c）可知，工业园区电功率来源主要为电网、燃气轮机、光伏和城市电网其他主体。由于园区中存在蓄热装置，因此电锅炉负荷在电价高峰时段分布较少，而电制冷机负荷在全天有较为均匀的分布。在光伏出力充足且园区内负荷较少的12:00—14:00 时段，工业园区向市政工作区送电获取收益。园区内的热功率首先由余热锅炉满足，剩余部分热功率主要来源于电锅炉。蓄热装置通过释热和吸热将低成本的热能转移到热能成本高的时段以减小全天能量费用。电锅炉烟气余热全用于供热，吸收式制冷机与电制冷机的最初能量来源均为电能，且电制冷机能效系数远大于吸收式制冷机，此时园区内冷负荷主要由电制冷机满足。

园区内电能交易如图4 所示。可见分布式主体1 保持全天向外送电，且在09:00—15:00 以及18:00—20:00 时段存在送电小高峰；分布式主体2主要在00:00—05:00以及19:00—24:00时段向外送电；分布式主体3 主要在11:00—15:00 时段向外送电；在电能缺口较大的时段（如10:00—15:00），受电能传输的限制，存在分布式主体3从分布式主体1购电向分布式主体2售电的情况。

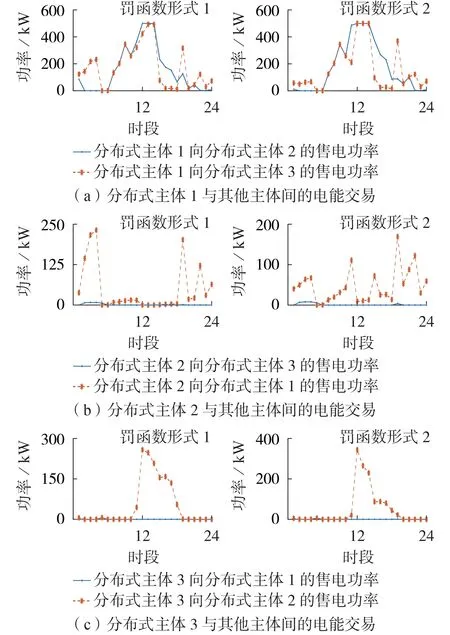
图4 分布式主体间电能交易曲线Fig.4 Energy trading curves between distributed agents

图5 展现了各主体分别采用2 种罚函数形式进行优化得到的主体之间交易电价。可见电价变化趋势与电网电价保持一致，较好地反映了真实情况。在03:00—05:00时段出现交易电价差异的原因可能是在该时段需求量小同时部分主体供给裕度小，在10:00—15:00时段出现交易电价差异的原因是需求量大同时部分主体供给裕度小。部分时段价格从不同方向偏离向电网购售电价格区间，其差异可能是由全时段最优与单时段最优造成的。

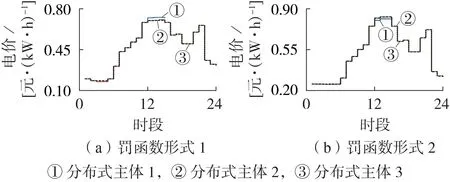
图5 各分布式主体售电电价Fig.5 Electricity price of distributed agents

根据图5可以发现，当主体采用2种罚函数形式策略时，得到的边际电价与电网电价变化趋势一致，电能交易量变化趋势基本一致，但罚函数形式2 的整体电价水平高于罚函数形式1。其原因是本文未区分初始认定电价，且两者在决策时对经济性以及协同性考虑程度不同，罚函数形式1 随市场供需变化不大，然而罚函数形式2 随供需变化有较大范围的波动。

迭代过程中功率容差与电价容差变化曲线如图6所示。可见采用罚函数形式1时，整体趋势是倾向于收敛的，出现残差细微增大的原因可能是在协调过程中可能出现全时段最优与单时段最优变化方向不一致。由图6（b）可见，残差出现先增大后减小的趋势是因为v′xy，t相比wxy，t存在增减趋势，使得前后2次交易优化结果差异明显。

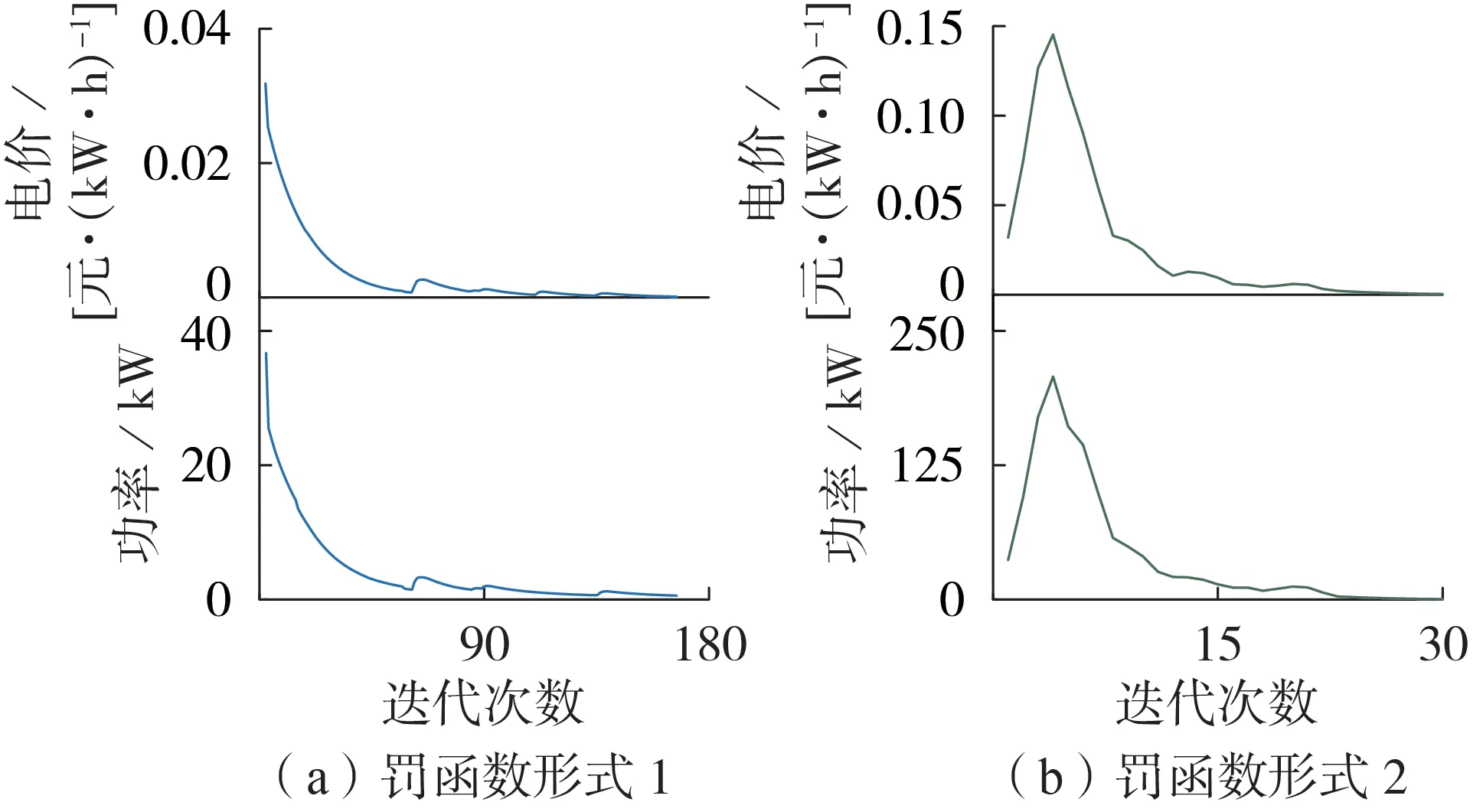
图6 功率容差与电价容差变化曲线Fig.6 Curves of variation of power tolerance and electricity price tolerance

4.2 与其他交易模式的对比分析

将以下3种交易模式进行对比分析，结果如表1所示。模式1，各分布式主体单独与电网进行电能交互，主体内自治优化，主体间无交易（放开各分布式主体与电网的交互功率限制），各主体利益分配固定；模式2，所有分布式主体以全网总体利益最优进行集中式优化，主体内部元件亦参与集中式优化，即为传统的集中式优化，无利益分配；模式3，本文所提的可交易能源模式，各主体之间存在利益分配。

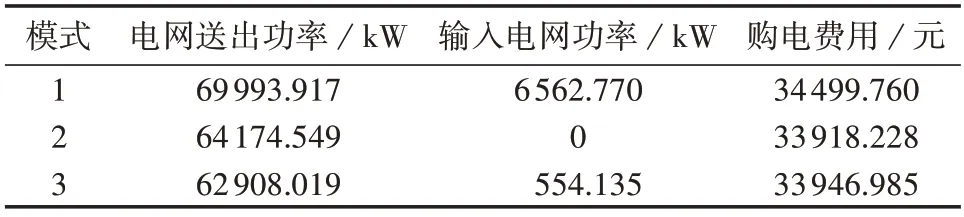
表1 不同交易模式对比Table 1 Comparison among different trading models

由表1 可知，城市配网侧进行能量互动，不论管理方式采用模式2 还是模式3，都能实现能源互补，降低与电网侧的电能交易，相较于模式1 而言实现整体购电费用下降。对比3种交易模式可知，模式1与电网的功率交互以及整体购电费用均最大；模式2的整体成本最优；本文所提的模式3与电网的电能交互总和最少，能量就地平衡能力最强，在保证电网与自身运行的经济性的同时，通过引导利益分配来反映各分布式主体的利益诉求。

4.3 分布式主体的协同策略影响分析

不同的罚函数形式反映了各主体对于其他主体的协同偏好。考虑3.2 节所述2 种罚函数形式的协同偏好，3个分布式主体共有26=64种策略组合。对所有策略组合进行遍历，分别对4.2 节的3 种交易模式进行仿真，得到3 种模式下系统总购电费用以及主体与电网交互功率之和，如图7 所示。由图7（a）可知，在所有策略组合下，分布式市场总购电费用仍维持在较低水平。由图7（b）、（c）可知，在所有策略组合下，从电网的购电功率仍能维持在最低水平，出售给电网的功率维持在模式1 与模式2 之间。不同组合形式下，分布式主体整体与电网之间的购电功率与售电功率均存在一定程度的波动。

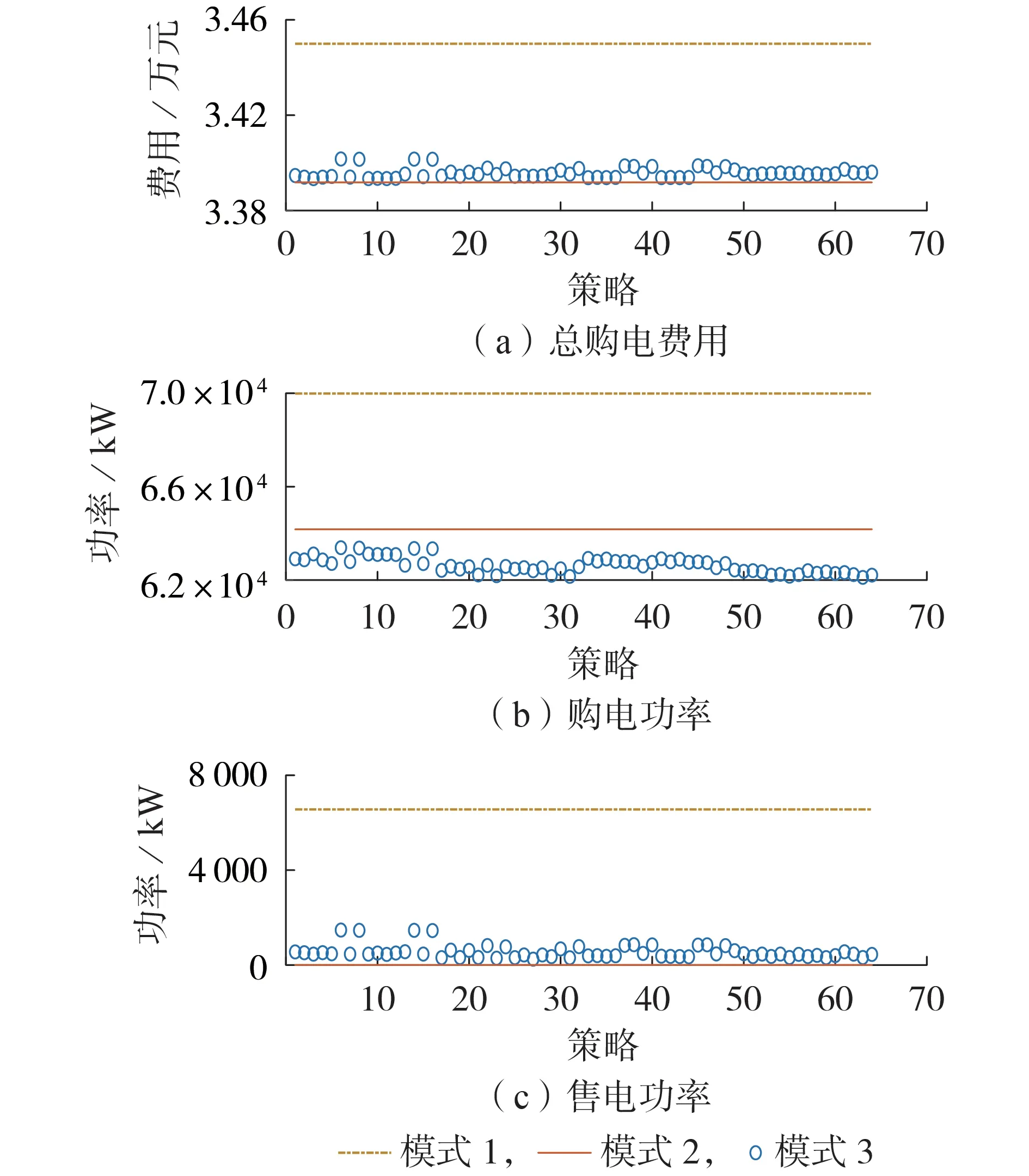
图7 所有策略组合下分布式主体整体情况Fig.7 Overall situation of distributed agents under all strategy combinations

考虑到首先模式2 结果中不存在各分布式主体间的利益分配，其次理论上，市场交易电价位于电网购售电价之间时，市场买卖方均能享受红利。为此，图8 分别对比了模式1 下分布式主体以电网购电费用向电网售电（模式1a）和模式1 下分布式主体以电网售电费用向电网售电（模式1b）2种情况。

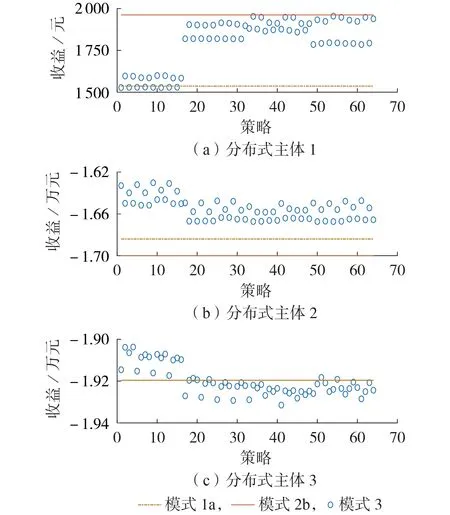
图8 所有策略组合下分布式主体利益分配Fig.8 Distribution of interests of distributed agents under all strategy combinations

图8（a）中分布式主体1 大部分组合收益处于模式1a 以及模式1b 之间，部分组合低于模式1a 的原因是分布式主体1 采用罚函数形式1 协调中牺牲了少部分经济利益。图8（b）中分布式主体2所有组合收益高于模式1 下分布式主体2 的收益。图8（c）中分布式主体3部分组合收益高于模式1，部分组合收益低于基准线的原因是某些时段分布式主体3 从电网的购电功率已经达到限值，此时分布式主体3 对于本地交易的需求是刚性的，使得形成的最终交易电价高于从电网的购电电价。为此提升分布式主体3 与电网交互功率为2 500 kW 时，其在所有策略组合下的收益见附录D 图D1，相较于图8（c），其获益的策略组合数以及整体收益均有所提升。针对62号策略（分布式主体1对分布式主体2采用罚函数形式2，对分布式主体3采用罚函数形式1；分布式主体2 对分布式主体1 和3 均采用罚函数形式2；分布式主体3 对分布式主体1 和2 均采用罚函数形式1）组合，逐渐提升主体3 与电网交互功率，最终收益能够高于模式1并稳定下来。

综合图7、8 可知在仅运用3.2 节形成的策略组合中存在各主体均能享受市场红利的组合。因此，本文所提可交易能源机制下，存在所有分布式主体均获利的空间。

为便于分析各形式下分布式市场主体间的利益分配，按每个主体对其他主体均采用同种ATC 罚函数形式进行组合缩减，则仅剩23=8 种组合形式，分别为111／112／121／122／211／212／221／222（按分布式主体1—3 的顺序排列，如111 表示3 个分布式主体对其余交易对象均采用罚函数形式1）。

表2 展示了各主体采用不同策略组合的收益，其中收益为负代表该主体呈消费者状态，收益为正呈销售者状态。针对分布式主体1，采用ATC 罚函数形式2带来的收益高于ATC罚函数形式1，其原因可能是分布式主体1 作为供给方，且市场供小于求。针对分布式主体2、3，作为需求方，采用不同ATC 罚函数形式带来的利益分配结果受限于其他分布式主体的策略以及市场供小于求的市场状况，2 种罚函数形式不存在明显的优劣。

表2 基于ATC的策略组合分析Table 2 Strategy combination analysis based on ATC

5 结论

本文基于ATC 设计了面向分布式主体的可交易能源模型，结合经济交易和系统优化运行两部分，为ATC 灵活性在系统优化运行提供经济学视角，并建立具体分布式主体的优化运行模型。

1）建立了冷热电联供机组、光伏、空调负荷等分布式主体物理元素模型。进一步地，基于ATC 理论，建立面向分布式主体的可交易能源模型。

2）对比了3 种交易模式下分布式主体能源就地消纳情况以及分布式市场购电成本，得出本文所提方法在反映市场主体经济行为的同时能够较好地实现就地消纳，保持总体经济性。

3）通过算例分析了含2种ATC罚函数形式，3个分布式主体构成的策略组合下，分布式主体整体效益以及所有利益分配，表明分布式主体整体效益以及与电网功率交互方面仍满足结论2），利益分配结果多样且合理，表明ATC 的灵活性在本文可交易能源机制下具有较好的应用前景。

4）本文在运用ATC 理论进行建模时仍采用全局性的收敛条件，而从本文可交易能源机制而言其收敛条件存在动态可变的可能性。此外，结论2）、3）并非一般性结论，仍受限于分布式主体的供需匹配程度等因素。

附录见本刊网络版（http：//www.epae.cn）。