基于改进协同演化算法的综合能源系统经济性与可靠性优化规划
林毓军,苗世洪,尹斌鑫,赵海彭,姚福星,杨志豪
(1. 华中科技大学 电气与电子工程学院 强电磁工程与新技术国家重点实验室,湖北 武汉 430074;2. 华中科技大学 电气与电子工程学院 电力安全与高效湖北省重点实验室,湖北 武汉 430074)
0 引言
随着能源危机和环境污染问题的日益突出,构建可持续发展能源体系、提高能源利用率已成为能源领域的研究重点。综合能源系统(IES)以电力系统为核心,耦合电、热、冷、气多种能源,通过各种能源生产、传输、储存、转换、分配等环节的协调优化,可以实现能源的高效利用,从而满足工业生产与居民生活的能源多样化需求[1-2]。近年来,IES在国内外引起了广泛的关注。相比于独立运行的能源系统,IES 的设备类型更加丰富,运行特性更为复杂,且不同能量流之间存在密切的耦合关系。因此,制定合理有效的规划方法是实现IES 高效、经济、可靠运行的重要前提[3]。IES 优化规划的基本思路是以经济性、可靠性为目标进行优化运行模拟,从而确定使目标最优的综合能源设备类型与容量配置。
针对IES 的优化规划问题,国内外学者已经进行了大量的研究。文献[4]考虑天然气管网、配电线路、燃气发电厂在内的选址定容,提出了包含电力系统和天然气系统的多阶段规划模型。文献[5]考虑到电转气设备对可再生能源的消纳作用,研究包含风电场的IES 优化规划问题,以最小化投资、运行与弃风成本为目标,建立协同规划模型。文献[6]在满足用户多种能源需求的前提下,以系统投资和用能成本之和最小为优化目标建立IES 规划模型,并采用改进Kriging 模型快速准确地得到系统最佳规划方案。上述研究在分析多能流耦合特性的基础上,建立IES 优化规划模型,表明采用合理有效的规划方案可以实现IES 经济运行。然而,以上文献仅针对IES 运行经济性进行优化,难以满足系统多维度优化规划的需求。进一步地,文献[7]针对计及电转气设备的IES,建立含经济性与可靠性的多维度评价指标体系。文献[8]提出了一种由经济性分层优化模型和可靠性校验模型组成的园区IES 规划模型,通过经济性优化模型和可靠性校验模型的循环迭代,从而兼顾规划方案的经济性与可靠性。文献[9]考虑分布式热电联产(CHP)机组对电力子系统运行可靠性的影响,以全周期净收益和可再生能源渗透率为优化目标建立规划模型。上述文献分析了IES可靠性对规划方案整体效益的影响,为IES 优化规划研究提供了一定的理论基础。然而,现有研究提出的规划模型大多是以IES 运行经济性为目标函数,可靠性仅作为经济性优化模型的辅助约束条件或后检验手段。随着生产方式的转变和人民生活质量的不断提高,用户对能源供应的可靠性提出了更高的要求[10]。国家能源局将在2021 年颁布《电力可靠性监督管理办法》,促进电能可靠性的提高[11]。此外,随着城市现代化水平的提高以及多能流耦合程度的加深,如何确保冷热能源的可靠供应成为亟待研究的问题。因此,在制定IES 规划方案时,有必要将经济性与可靠性置于统一标准下进行衡量优化。
为此,本文提出了基于改进协同演化算法(ICEA)的IES 经济性与可靠性优化规划方法。首先,在多场景经济性评估模型与基于马尔科夫链蒙特卡洛(MCMC)法供能可靠性评估模型的基础上建立IES多目标优化模型;然后,结合正交试验法计算决策变量对经济性与可靠性的影响因子矩阵,将决策变量进行分组获得经济性和可靠性演化子种群的变量集合;最后,通过经济性和可靠性子种群的种群间交互协同以及种群内部演化,求解多目标优化模型的Pareto 解集。算例结果表明本文模型所获得的规划方案可实现经济性与可靠性的协调优化。
1 IES经济性与可靠性评估模型
1.1 IES基本运行模型
本文所研究的IES 包含冷、热、电和气4 种能源形式。IES 内主要包括CHP 机组、热泵、电制冷机、吸收式制冷机、燃气锅炉、蓄电池、储热器和储冷器等设备。IES 结构如图1 所示。在源侧,系统通过集中式母线与燃气管道从能源辅助市场中购买电量与天然气,同时系统配置风电机组以充分利用内部的清洁能源;在荷侧,IES 通过CHP 机组、风电机组出力和电力市场购买电量来满足居民用电需求,热负荷由CHP 机组、热泵和燃气锅炉共同提供,冷负荷由电制冷机和吸收式制冷机联合供应;蓄电池、储热器和储冷器共同组成综合储能装置,有助于系统内多种能量在不同时间段内的协调调度和转移,使系统运行更加安全经济。
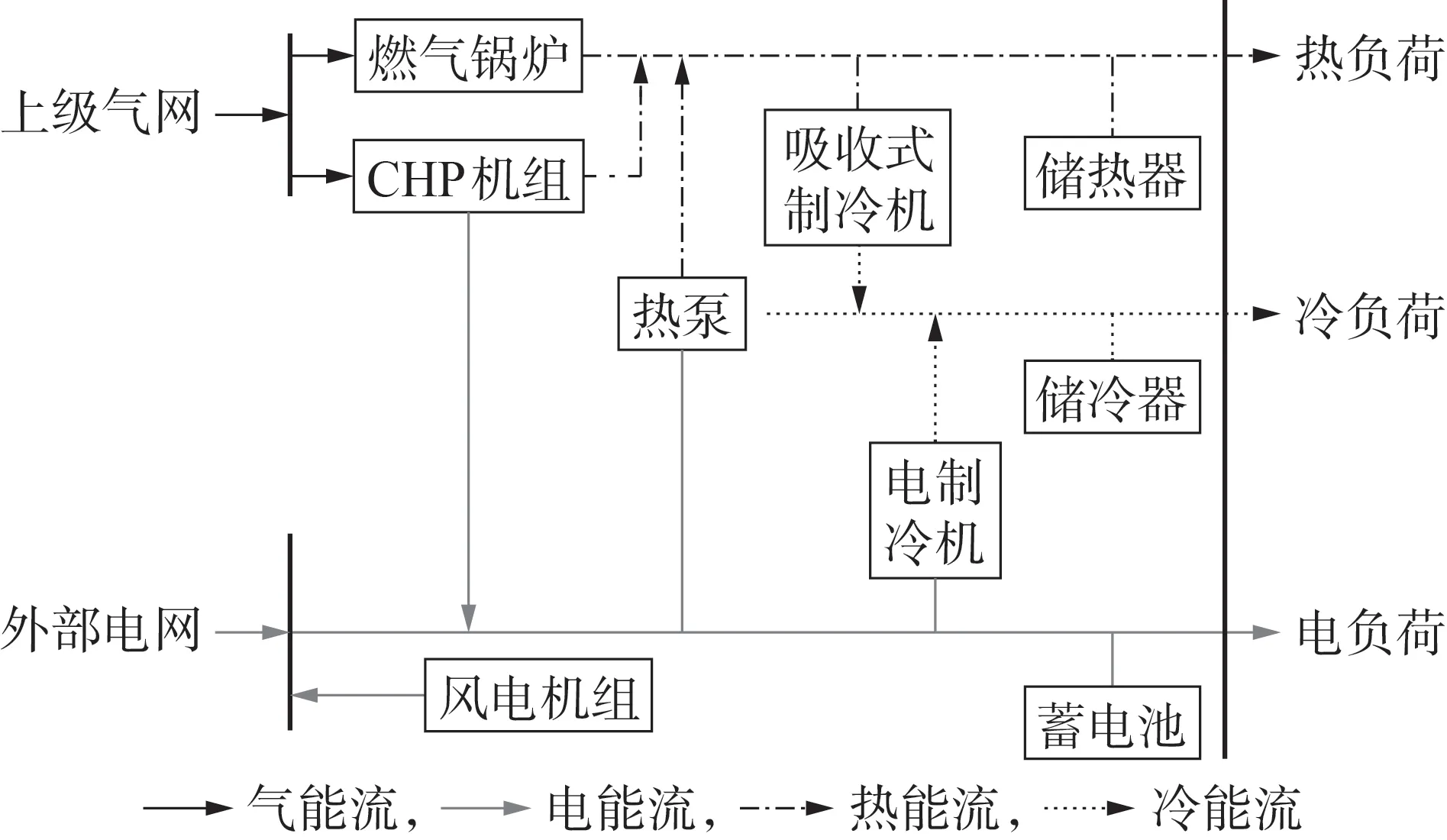
图1 IES结构Fig.1 Structure of IES
IES运行场景的多样化和不同能流之间的耦合,导致难以用解析法描述元件运行状态与系统经济性和可靠性之间的数学关系。因此,本文构建多场景下经济性评估模型与基于MCMC法的供能可靠性评估模型对IES运行的经济性和可靠性进行合理评估。
1.2 多场景下经济性评估模型
针对不同典型场景下多能流负荷需求不同的特点,本文提出多场景下经济性评估模型,通过优化运行方式,从而合理评估运行的经济性。模型的输入为设备的配置容量,输出为系统最小年化运行成本。
1.2.1 目标函数
本文以IES 的年化运行成本最小为目标,优化系统的运行方式,从而获得经济性评估结果。其目标函数为:
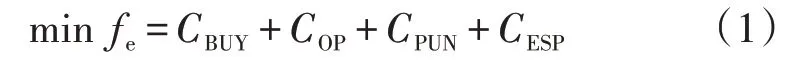

1.2.2 约束条件
针对所研究的小型IES,本文主要考虑设备运行约束和多能流系统功率平衡约束。由于小型IES 中网络拓扑结构较为简单,网络线路较短,能量传输损耗较小,因此本文忽略多能源网络的物理运行约束,仅计及系统的多能流功率平衡[13]。
1)CHP机组约束。
本文采用背压式燃气轮机作为CHP 机组,其输出电功率、热功率和耗气量之间的关系为:

式中:uCHP,t为CHP 机组的运行状态变量,uCHP,t=1 时表示CHP 机组处于运行状态,uCHP,t=0 时表示CHP机组处于关闭状态;PCHP_min、PCHP_max和HCHP_min、HCHP_max分别为规划方案中CHP 机组的最小、最大输出电功率和热功率。
2)电功率平衡约束。
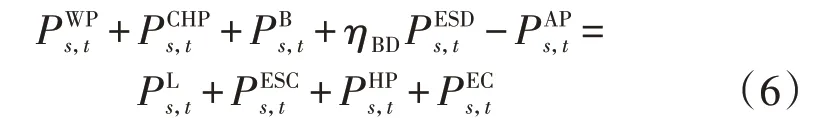

此外,燃气锅炉、热泵、吸收式制冷机、电制冷机、蓄电池、储热器、储冷器、风电机组的详细运行模型以及天然气流量平衡约束可参见文献[14]。
1.3 基于MCMC法的供能可靠性评估模型
针对IES 中各种能源形式之间存在复杂的相互转化关系和耦合关联的特点,本文建立基于MCMC法的供能可靠性评估模型。相比于随机采样的蒙特卡洛方法,MCMC 法考虑了系统状态间的相互影响,克服了蒙特卡洛法的静态限制,通过设备两状态模型和Gibbs 采样器获取系统的运行状态样本,从而快速计算得到系统负荷期望断供容量,加快了评估速度。模型的输入为设备的配置容量,输出为系统负荷断供容量期望值。
1.3.1 MCMC采样方法
MCMC 采样方法在传统的蒙特卡洛模拟中引入马尔科夫链状态转移矩阵,考虑了时间序列元素之间的关联性,通过重复采样,建立一个平稳分布与系统先验概率分布相同的马尔科夫链,从而得到可靠性评估的状态样本[15]。对于IES 中的多类型设备,其运行状态s(t)是一种随机过程,可采用如图2所示的两状态模型进行建模。两状态模型中,设备仅有正常和故障2 种状态,根据设备的参数可得状态转移模型如式(9)所示。
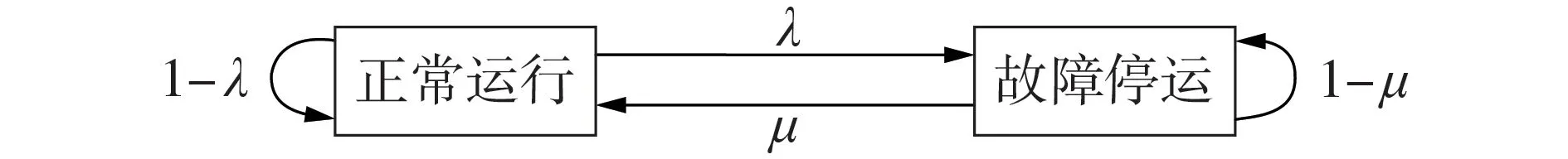
图2 两状态模型Fig.2 Two-state model
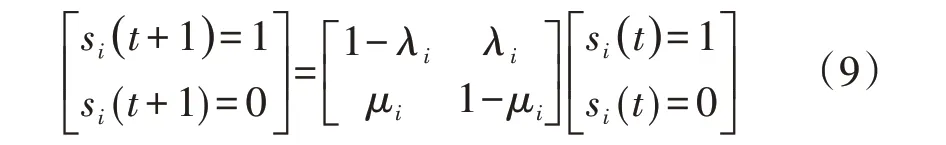
式中:si(t)=1表示设备i正常运行,si( )t=0表示设备i因故障停运;λi、μi分别为设备i的故障率和修复率。
基于设备两状态模型,本文使用Gibbs 采样器来产生MCMC 法中所需的马尔科夫链。假设IES 中需要采样的设备个数为m,则Gibbs 采样器中的第k个样本S(k)可表示为:
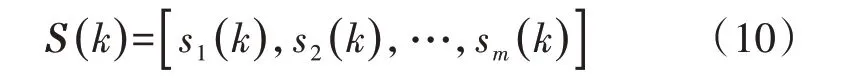
考虑到用于可靠性采样的MCMC法具有较强的收敛能力和较低的计算复杂度,且计算结果较为稳定,因此,本文设定最大采样样本量为N。当Gibbs采样器所采集的系统状态样本量大于最大采样样本量N时,模型认为采集到的样本为已经达到平稳分布的马尔科夫链,可以代表IES的实际运行状态。
假设IES 内设备运行状态转移过程是相互独立的,给定初始状态下所有设备均为正常运行的条件,Gibbs采样器的工作流程如下。
1)设定状态转移次数阈值为N1,需要采样的样本数为N2,则最大采样样本量N=N1+N2。
2)根据系统当前状态S(k)获取状态转移条件分布π,产生服从均匀分布U(0,1)的随机数u与条件分布进行比较,从条件分布π(s1|s1(k),s2(k),…,sm(k))中抽取设备1下一时刻的运行状态s1(k+1)。重复m次,直至完成状态S(k+1)的抽取[16-17]。
3)令k=k+1,判断采样次数是否大于最大采样样本量,若是则认为采样完成,否则重复步骤2)再次进行采样,直至获得所需样本数。
1.3.2 最小负荷断供容量模型
通过MCMC 采样获得IES 可靠性评估的状态样本后,本节建立IES 的再调度优化模型,求解故障状态下IES 的优化运行方式和最小负荷断供容量。设再调度模型中调度周期为24 h,单位调度时长为1 h。模型的目标函数和约束条件具体如下。
1)目标函数。
再调度模型以购能成本、运行成本和负荷断供惩罚成本之和最小为目标函数,如式(11)、(12)所示。

2)约束条件。
当系统内的设备发生故障后,需要在经济性评估模型约束条件的基础上修改设备出力约束和功率平衡约束中的负荷项,如式(13)、(14)所示。

1.3.3 可靠性评估流程
结合可靠性评估的状态样本和最小负荷断供容量模型可获得IES 在故障状态下的最小断供容量。在此基础上,本节采用能量不足期望值(EENS)指标评估IES 规划方案的可靠性。EENS 指在被研究的状态样本中系统负荷断供容量的期望值[18],计算公式如式(15)所示。
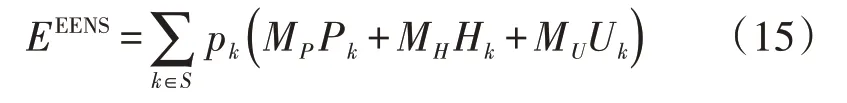
式中:EEENS为负荷断供容量期望值;S为状态样本集合;pk为状态样本k出现的概率;Pk、Hk、Uk分别为状态样本k对应的电负荷、热负荷和冷负荷断供容量值,MP、MH、MU为相应的加权系数。
基于上述研究,本节提出基于MCMC 采样方法的IES可靠性评估方法,具体流程见附录A图A1。
可靠性评估流程具体实施步骤如下:
1)初始化,输入设备的故障率和修复率、风电输出功率和冷热电负荷数据,输入最大采样样本量N;
2)设置所有设备的初始状态均为正常运行,利用MCMC法采样获取可靠性评估所需的样本;
3)判断状态样本k中系统内是否有设备发生故障,若有则转至步骤4),否则转至步骤5);
4)通过求解最小负荷断供容量模型,计算状态样本k下系统的负荷断供容量;
5)判断仿真次数是否小于最大值,若小于则重复步骤2)—4)进行下一个状态样本的仿真,否则结束仿真并输出可靠性评估指标。
1.4 考虑经济性与可靠性的IES 多目标优化规划模型
在上述模型的基础上,本节建立计及经济性与可靠性的IES 多目标优化规划模型。模型的目标函数为最小化系统年化运行成本和最小化故障状态下的负荷断供容量期望值,如式(16)所示。
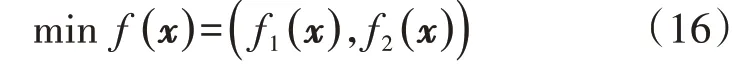
式中:f1(x)、f2(x)分别为经济性和可靠性优化目标函数。模型的决策变量为CHP 机组、燃气锅炉、吸收式制冷机、电制冷机、热泵、蓄电池、储热器和储冷器的规划容量。由于各类设备的配置容量受场地、可用投资成本、最小规划单元容量等多方面因素的限制,因此设备的规划容量为一系列离散的取值:
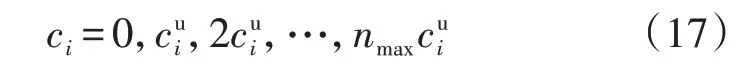
式中:ci为设备i的规划容量;为设备i的最小规划单元容量;nmax为最大可用规划单元数。规划模型产生一组设备规划容量,将其分别输入经济性评估模型和可靠性评估模型,从而得到规划方案对应的系统年化运行成本和负荷断供容量期望值。
2 基于ICEA的模型优化求解方法
系统负荷水平的提升和用户需求的多样化对IES运行的经济性与可靠性提出了更高的要求,然而经济性与可靠性的提升往往是以牺牲对方为代价的,难以得到兼顾经济性与可靠性的规划方案。
为此,本文提出了一种基于ICEA 的模型优化求解方法。该方法在考虑规划方案经济性与可靠性之间制约关系的基础上,采用正交试验法计算决策变量对系统经济性与可靠性的影响因子,进而构建经济性演化子种群与可靠性演化子种群,以便对规划方案进行针对性的优化。通过经济性子种群与可靠性子种群的种群间交互协同和种群内部演化,获取兼顾经济性与可靠性的规划方案。相较于传统的协同演化算法,本文方法引入了正交试验法预处理环节和最优个体协同机制,有效实现了IES 经济性与可靠性的协调优化。
2.1 基于正交试验法的决策变量分组方法
正交试验法利用标准化正交表安排试验方案,并对结果进行计算分析,从而确定各因素对目标函数的影响程度[19]。正交表可简单表示为Laˉ(bˉcˉ),其中aˉ为需实施试验的次数,bˉ为因素的水平数,水平数是指因素在试验时所选取的不同值,cˉ为正交表的列数,每一列可安排一个因素。
在IES 优化规划模型中,CHP 机组、燃气锅炉、电制冷机等设备的容量均会影响系统运行的经济性与可靠性。然而,不同设备的容量变化对规划方案的经济性与可靠性影响程度不同。为了获取设备容量对系统运行经济性与可靠性的影响因子矩阵,以便对规划方案进行针对性的优化,本文提出一种基于正交试验法的决策变量分组方法,计算步骤如下。
1)根据IES 经济性评估模型和可靠性评估模型对设备规划方案进行优化,分别得到以经济性和可靠性为单目标的最优解。
2)基于IES 规划模型中待规划的设备数量(因素数)选取合适的正交水平表。结合步骤1)中的结果分别选取临近单目标最优解的水平,从而安排部分试验的规划方案,计算出不同规划方案对应的系统运行经济性和可靠性。
3)采用极差分析法分别计算各决策变量所有取值对应的目标函数的平均值,并由此计算出各决策变量关于经济性与可靠性的影响因子。
4)根据影响因子矩阵,计算模糊隶属度,从而将决策变量进行分组,构造经济性演化子种群和可靠性演化子种群。
2.2 基于ICEA的模型优化求解
协同演化算法借鉴自然界中的协同演化机制,通过将复杂系统的优化问题分解为多个子系统的优化问题,并且在演化过程中考虑不同种群间动态的选择决策和相互作用的过程,从而实现系统整体的优化[20]。
假设图3 为正交试验法的分组结果。在协同演化算法中,将经济性与可靠性作为模型的优化目标,分别生成2 个种群。每个种群中有若干个个体,每个个体记录一个决策向量与针对特定目标的评估值,此外,种群中保留当前的最优个体及其评估值。种群间交互协同机制如图4所示。

图3 基于正交试验法的分组结果Fig.3 Grouping results based on orthogonal test method
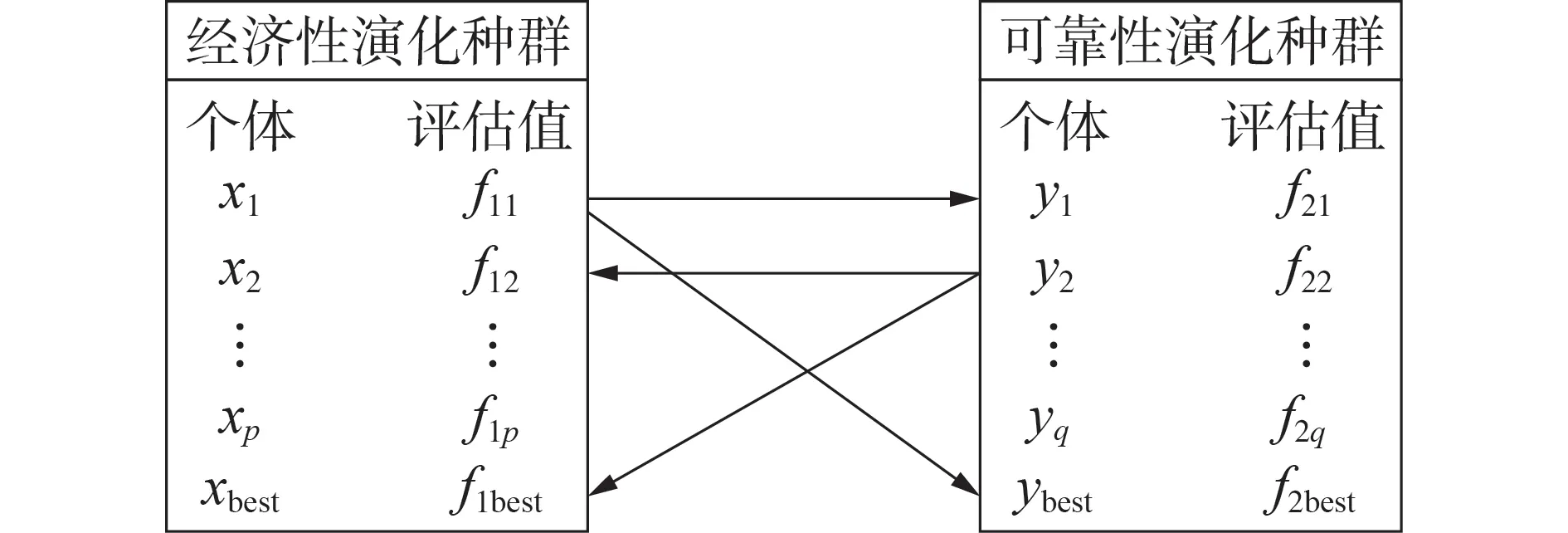
图4 种群间交互协同机制Fig.4 Interaction and synergy mechanism between populations
改进协同演化算法借鉴了合作型协同进化算法的思想,当经济性优化种群中的个体xi=[li1,li2,…,lip] 与 可 靠 性 优 化 种 群 中 的 个 体yj=[kj1,kj2,…,kjq]交互时,二者协同构成一个完整的规划方案分别进行经济性评估与可靠性评估。其中,将经济性评估结果作为xi在本次交互协同过程的收益值g1,ij,可靠性评估结果作为yj的收益值g2,ij。
在演化算法的每一代,改进协同演化算法分别从2 个种群中随机挑选成对的个体进行若干次协同交互[21]。被挑选的个体与另一个种群的最优个体额外进行一次协作评估。当交互完成后,将个体的评估值定义为所有协同交互中所获取的收益值的最优值:
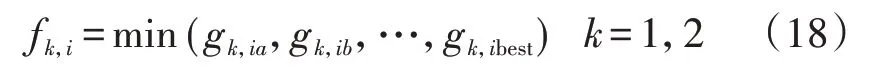
式中:k=1 时表示经济性优化种群个体,k=2 时表示可靠性优化种群个体;fk,i为个体i在本轮交互协同过程中的评估值;gk,ia、gk,ib分别为个体i与个体a、个体b交互协同的收益值;gk,ibest为个体i与最优个体交互协同的收益值。通过最优个体协同机制,改进协同演化算法可以提高种群个体的趋优性,从而更有效搜索到Pareto前沿面。
在采用种群间交互协同获取个体的评估值后,本文采用差分进化算法分别对每个种群进行演化,生成子代种群。差分进化算法是一种基于群体差异的启发式随机搜索算法,具有记忆种群内个体最优解和种群内信息共享的特点,主要包括变异、交叉和选择3个基本操作[22]。
1)变异。差分进化算法通过差分策略实现个体变异,对于第g代个体的变异操作,具体如下:
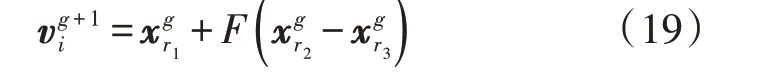
2)交叉。交叉操作的目的是随机选择个体,增加种群的多样性,具体如下:
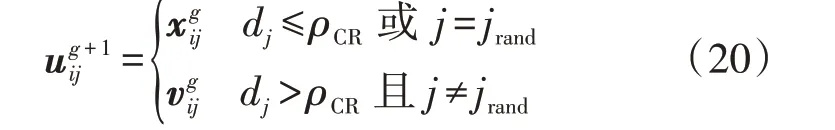
3)选择。差分进化算法采用贪婪选择的策略,选择较优的个体作为新个体:
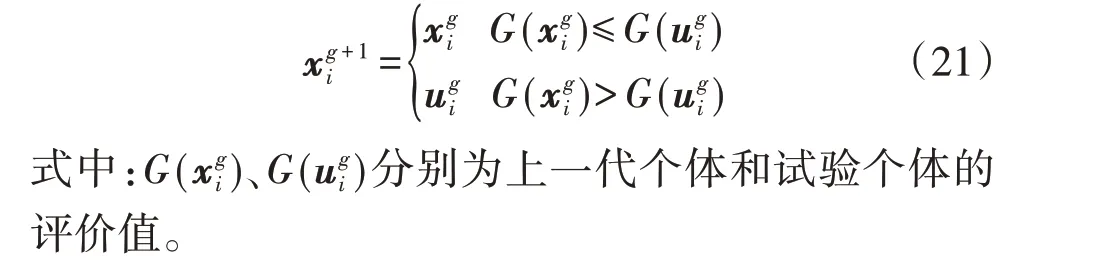
综上所述,本文所提模型的具体优化流程如图5所示。
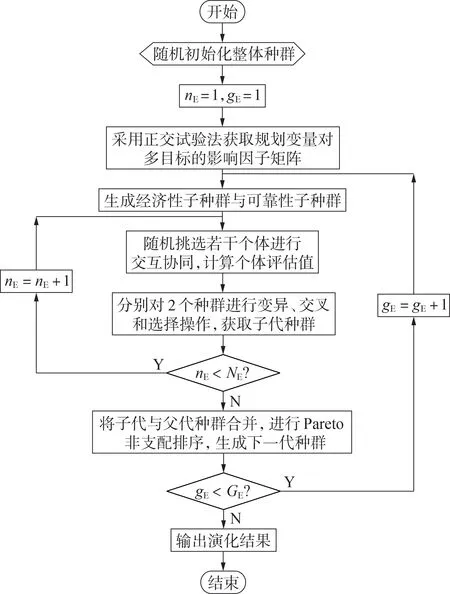
图5 基于ICEA的模型优化流程Fig.5 Model optimization process based on ICEA
1)初始化。输入设备最大规划单元数量、设备经济性评估参数与可靠性评估参数、子种群最大进化次数NE和算法最大迭代次数GE。
2)采用正交试验法进行分组预处理,获取决策变量对系统经济性与可靠性的影响因子矩阵。
3)根据影响因子矩阵将决策变量分为经济性子种群和可靠性子种群。
4)在每一轮交互中,分别从2 个子种群中随机挑选若干个个体组成完整决策变量进行经济性评估和可靠性评估,根据式(18)计算个体评估值。
5)采用差分进化算法对2 个子种群分别进行变异、交叉和选择操作,各自生成下一代子种群。
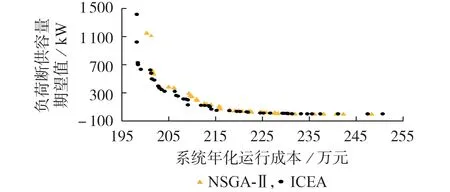
6)判断子种群演化次数是否满足nE 7)将子种群与父代种群合并,进行Pareto 非支配排序和拥挤度计算,并基于精英保留策略生成下一代整体种群。 8)判断算法迭代次数是否满足gE 由于本文模型求解得到的是Pareto 前沿解集,而在实际规划过程中,IES投资商会根据对经济性与可靠性的偏好程度从Pareto 最优解集中选择特定规划方案。为了描述IES 投资商的偏好程度,本文对系统经济性与可靠性进行归一化,从而获得IES 投资者关于规划方案的经济性与可靠性的效用函数F*,如式(22)所示。 式中:f1max、f1min分别为Pareto解集中经济性成本的最大值和最小值;f2max、f2min分别为Pareto解集中负荷断供容量的最大值和最小值;A、B分别为IES关于经济性和可靠性的偏好系数,满足A+B=1。通过选取不同的A、B值,可以获得不同偏好下的IES 投资者的最优方案。 本文的优化模型涉及到混合整数线性规划问题的求解,因此采用Pycharm2019.3.x64 调用Gurobi优化求解器进行求解,优化建模平台为Intel Xeon Gold 6148,主频为2.4 GHz。 取某地区的IES 实际参数进行仿真分析。算例中将全年划分为过渡季、供冷季与供热季3个典型场景,比例为61∶153∶151。附录A 图A2—A4 为3 个典型日的风电出力和电热冷负荷,根据该数据进行系统设备容量规划。根据文献[23],购电市场采用分时电价形式,其中谷时段01:00—08:00、23:00—24:00为0.24 元/(kW·h),平时段09:00—11:00、21:00—22:00 为0.57 元/(kW·h),峰时段12:00—20:00 为0.95 元/(kW·h)。购气价格为2.37 元/m3。CHP机组、燃气锅炉等设备建设单元的运行规划参数见附录A 表A1—A3[24-25]。调度周期T=24 h,单位时间间隔为1 h。工程周期取20 a,折现率r取8%。设备的最大规划单元取10。算法参数设置中,最大采样样本量取876 000。电负荷、热负荷和冷负荷断供容量加权系数取MP∶MH∶MU=2∶1∶1。整体种群规模取150,算法最大迭代次数GE取50,子种群的最大演化次数NE取3。 根据经济性评估模型和可靠性评估模型,分别对IES 经济性与可靠性2 个目标进行单目标优化规划。其中,由于可靠性评估模型主要是面向现有规划方案计算负荷断供容量期望值,评估其运行可靠性水平,无法根据可靠性目标完成设备容量配置优化。因此,本文采用差分进化算法获取可靠性单目标优化解,通过启发式搜索得到负荷断供容量最小对应的IES 规划方案。单目标优化结果如附录A 表A4所示。 本文所提出的优化模型为一个有8 个决策变量、2 个优化目标的多目标优化问题,故选取三水平正交试验表L27(313)进行试验方案的设计。由于表中列数大于决策变量个数,依据正交表的正交性,本文算例选取前八列安排正交试验方案,从而获取决策变量对目标函数的影响因子矩阵。基于单目标的优化结果,分别进行经济性与可靠性的正交试验表设计,设计结果见附录A 表A5 和表A6。采用极差法对正交试验的结果进行分析,可得到CHP 机组、燃气锅炉等设备对经济性与可靠性的影响因子矩阵如附录A表A7所示。 结合影响因子矩阵和模糊隶属度计算结果可以看出,经济性子种群由CHP机组、电制冷机和吸收式制冷机的规划容量组成;可靠性子种群由燃气锅炉、热泵、蓄电池、储热器和储冷器的规划容量组成。 基于经济性与可靠性子种群划分结果,本文在相同演化次数下采用所提ICEA 和非支配排序遗传算法(NSGA-Ⅱ)求解IES 多目标规划模型,所获得的Pareto前沿解集和运行时间对比如表1和图6所示。 图6 NSGA-Ⅱ和ICEA优化结果对比Fig.6 Comparison of optimization results between NSGA-Ⅱand ICEA 表1 ICEA和NSGA-Ⅱ运行时间对比Table 1 Comparison of running time between ICEA and NSGA-Ⅱ 从ICEA 所获取的Pareto 前沿解集可以看出,随着系统规划方案可靠性的提高,系统运行的经济性随之下降。为了减少IES 故障状态下负荷断供容量,系统必须考虑增设储能设备或者提高能流转换设备的冗余度,而设备的扩建必然会增加系统投资成本,降低规划方案的经济性。IES 优化规划模型充分考虑规划资源的限制以及经济性与可靠性之间相互制约的关系,实现了系统经济性与可靠性的协调提升,满足现代能源利用的多样化需求。对比NSGA-Ⅱ和ICEA 的优化结果可知,在相同的演化次数下,本文提出的ICEA 运行时间更短,搜索得到的规划方案能够很好地逼近多目标优化模型的Pareto前沿,此外,规划方案分布的多样性也得到了较好的改善。相较于NSGA-Ⅱ,ICEA 引入了正交试验法预处理环节和种群交互协同机制。一方面,ICEA 通过正交试验法对决策变量进行预分组处理,减小了搜索空间维数,从而针对性地优化规划方案的经济性与可靠性,提高算法运行速度;另一方面,通过不同种群之间随机个体与最优个体的交互协同,并保留最优值作为个体的收益,提高了种群个体的趋优性,从而更有效搜索到Pareto 前沿面,改善算法的计算精度。通过对比算例结果验证了本文所提算法的有效性和优越性。 为了说明所提模型和算法可以实现系统规划方案经济性与可靠性的协调优化,在获得模型Pareto前沿解集的基础上,对IES 投资者关于规划方案经济性与可靠性的不同偏好程度进行假设,共设置了以下5 种场景,从而根据IES 投资者的不同效用函数,从Pareto最优解集中获取优化规划方案。 1)场景1:IES 投资者以完全倾向经济性的偏好程度从Pareto 前沿解集中获取规划方案,取效用函数的偏好系数为A=1,B=0。 2)场景2:IES 投资者以更倾向经济性的偏好程度从Pareto 前沿解集中获取规划方案,取效用函数的偏好系数为A=0.7,B=0.3。 3)场景3:IES 投资者关于规划方案的经济性与可靠性并无明显偏好,取效用函数的偏好系数为A=0.5,B=0.5。 4)场景4:IES 投资者以更倾向可靠性的偏好程度从Pareto 前沿解集中获取规划方案,取效用函数的偏好系数为A=0.3,B=0.7。 5)场景5:IES 投资者以完全倾向可靠性的偏好程度从Pareto 解集中获取规划方案,取效用函数的偏好系数为A=0,B=1。 结合式(22)对Pareto 解集中的规划方案进行效用函数的计算,可得到4 种场景下系统的最优规划方案以及对应的经济性与可靠性优化值如附录A 表A8所示。 从不同场景下的规划方案优化结果可以得出,随着IES 投资者对可靠性偏好程度的增加,最终选择的规划方案对应的负荷断供容量随之减小,系统运行经济性也随之下降,验证了规划方案是通过牺牲系统的经济性从而换取可靠性的提升。优化结果表明,本文所构建的模型可以实现规划方案经济性与可靠性的协调优化,从而为不同偏好的IES 投资者提供决策参考依据。 此外,从IES 投资者不同偏好程度下设备规划容量结果可以看出,随着IES 投资者对可靠性偏好程度的增加,规划方案中储能设备的配置容量增加最为明显。实际系统中,设备的修复率往往高出故障率几个数量级,设备故障时间仅持续短暂几个小时便恢复正常运行。储能设备通过能量的快速存储与释放,实现能量在不同时段的转移,从而在设备发生故障时短暂地提供功率支撑,减少不必要的负荷断供容量,提高系统可靠性。 对比IES 投资者仅偏好经济性和仅偏好可靠性的优化结果可知,相较于场景1,场景5 获得的优化规划方案中燃气锅炉、热泵、电制冷机和多能流储能设备的配置容量均有所增加,而减少了CHP 设备配置容量。这是由于当所有设备尤其是储能设备的规划容量达到一定限值时,系统的负荷断供容量期望值已减少到0。此时,再增加CHP 设备投资容量给规划方案可靠性带来的边际提升较小,设备投资量的冗余反而会降低规划方案的经济性。综上所述,本文所提模型可以根据IES 投资者的偏好获取合理的规划方案,实现经济性与可靠性的协调提升。 为了进一步分析可靠性评估模型中电负荷、热负荷和冷负荷断供容量加权系数取值对规划方案结果的影响,本文在场景3对应的IES投资者效用函数(A=0.5,B=0.5)的基础上设置以下4 种加权系数取值场景,对比不同加权系数下IES 设备最优容量配置结果。 1)场景6:可靠性评估模型中电负荷、热负荷和冷负荷断供容量加权系数MP∶MH∶MU=4∶1∶1。 2)场景7:可靠性评估模型中电负荷、热负荷和冷负荷断供容量加权系数MP∶MH∶MU=2∶1∶1。 3)场景8:可靠性评估模型中电负荷、热负荷和冷负荷断供容量加权系数MP∶MH∶MU=2∶3∶3。 4)场景9:可靠性评估模型中电负荷、热负荷和冷负荷断供容量加权系数MP∶MH∶MU=1∶3∶3。 求解得到不同加权系数取值下IES 规划方案以及多能流系统负荷断供容量期望值如附录A 表A9所示。 对比不同加权系数下IES 设备容量配置结果可知,随着可靠性评估模型中冷、热负荷断供容量加权系数的增大,IES 投资者会减少部分蓄电池的建设,转而增加电制冷机、热泵和储热器等设备容量,以减少热、冷子系统负荷断供容量期望值,从而优先提升热、冷子系统运行可靠性水平。通过可靠性评估模型中电负荷、热负荷和冷负荷断供容量加权系数的合理取值,IES多目标优化规划模型可以反映投资者关于电、热、冷能流系统运行可靠性水平的提升优先级。 本文在经济性评估模型和可靠性评估模型的基础上构建IES 多目标优化规划模型,并结合正交试验法提出了一种基于ICEA的模型求解方法,通过仿真算例分析得出以下结论。 1)在充分考虑规划方案经济性与可靠性之间制约关系的基础上,建立IES 多目标优化规划模型。该模型相较于仅考虑经济性的单目标优化规划模型,可以实现系统经济性与可靠性的协调提升,满足现代能源利用的多样化需求。 2)ICEA 引入了正交试验法预处理环节和种群交互协同机制,一方面针对性地优化规划方案的经济性与可靠性,提高了算法运行速度;另一方面通过不同种群之间随机个体与最优个体的交互协同,提高种群个体的趋优性,改善了算法计算精度。 3)IES 多目标优化规划模型可以根据投资者的偏好设定效用函数的偏好系数,为不同偏好的IES投资者选取合适的规划方案,作为其决策参考依据。 附录见本刊网络版(http://www.epae.cn)。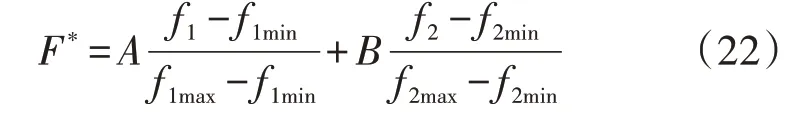
3 算例分析
3.1 算例参数设置
3.2 决策变量分组结果
3.3 模型优化结果分析

3.4 经济性目标与可靠性目标的协调优化
4 结论

