基于损失贫化率定量预测的矿山经济优化

陈彦亭 陈 越 杨 顺 刘东升 李金龙 巩瑞杰

（1.河北钢铁集团矿山设计有限公司；2.河北钢铁集团矿业有限公司；3.正元国际矿业有限公司）

矿山技术经济指标是衡量矿山企业经营效果、生产技术、管理水平的重要依据，其优化技术和过程建模一直是学术热点［1-3］。研究目标亦从单个因素或少数几个因素的优化发展为与经济评价相结合的多决策变量的整体动态性优化。大部分单因素研究都是以边界品位、工业品位因素为重点，多决策变量的优化研究则是考虑诸多因素，将矿山的生产管理纳入一个整体去考虑［4］。我国铁矿山的数量众多，类型各异，但大多技术先进的矿山对经营参数的优化都非常重视，每当市场变动或技术变革之时都会对经营参数进行及时调整，只有这样才能保证它们的生产经营处于合理的状态，也只有这样才能保证矿产资源得到最有效的开发和利用［5］。

司家营北区是河钢集团矿业公司主要生产基地之一，规模大、供矿点多，生产组织复杂，具有其自身独特性，以往研究成果的适用性不佳。鉴于现代企业的发展趋势和司家营北区的具体情况，为了取得更佳的企业整体经济效益，开展了本项研究。本研究参考多决策变量优化研究模式，以多年累积的生产数据为基础，以产品指标（如精矿品位、尾矿品位）稳定不变为约束条件，以强化管理调节损失贫化率为手段，以达到经济效益最大化的目标。采用回归分析与规划求解等数学手段建立综合技术经济评价数学模型并求解，对矿山的技术经济指标进行优化，并用得出的优化结果指导生产。

1 矿山生产概况

河钢集团矿业公司是国有大型黑色冶金矿山企业，公司矿产资源丰富，研究依托矿山为其下属大型露天矿山之一——司家营北区露天矿。矿山矿床为“鞍山式”沉积变质铁矿床，矿石主要赋存于黑云变粒岩中，采用深凹露天开采模式，采场内矿、岩均由自卸卡车运至采场西南总出入沟口外的矿、岩粗破碎车间，破碎后的矿石由矿石胶带运输系统运至选矿厂，进入磨矿选别系统，最终生产出铁精矿；破碎后的岩石经胶带运输系统运至岩石排土场或经铁路运输至曹妃甸填海造地。

司家营北区作为矿业公司的主体矿山，所采用的工业指标多是当年上级主管部门基于行业的整体情况下达的。目前矿山所处的市场环境、资源状况、生产技术条件与当时相比都已经发生了很大的变化，生产环节技术改造升级也仅是局部调整，没有从矿山整体生产经营的角度出发。本次针对司家营北区露天矿及选矿厂的实际情况，对其生产的各工艺技术环节进行深入研究，挖掘隐藏于它们之间的动态、有机联系，建立综合技术经济评价体系，为矿山生产经营提供决策支持，实现矿山技术指标整体、动态优化方式在实际生产中的应用。

2 矿山技术经济优化模型

2.1 研究方法

矿山技术经济指标优化研究是一项非常复杂的工作，综合性强，涉及到资源条件、生产技术、经济和管理等诸多因素［6-8］。本研究通过调查分析司家营北区多年生产积累的实际数据，根据整体性与动态性原则，利用回归分析法建立以损失率、贫化率为重点的研究对象，以采、选、售为整体，以经济效益最大值为目标函数的技术经济指标数学模型，并采用规划求解法来寻求此模型的最优解。具体优化流程见图1，模型求解出的损失贫化率即为经济效益最大化时的对应值，即理论上最优，用以指导现场生产，使矿山经济效益更优。

2.2 损失率、贫化率关系模型

建立损失率、贫化率关系数学模型最常用的方法就是通过收集矿山的损失率、贫化率历史生产数据，研究建立其数学回归模型。但该矿矿体多呈层状或似层状，部分呈透镜状或扁豆状，受构造和古地形的影响，厚度变化较大，形态变化较复杂，沿走向和倾向均有突然尖灭、分枝复合和膨缩现象。因此不同区域范围回归出的数学模型会有差异，全矿区的回归方程并不能完全适用于小的开采区域。借助三维模型，在进行小范围区域预测时充分考虑预测区域的空间形态、矿体产状、矿岩关系、台阶高度及电铲采剥方向等因素，选择最适合的函数关系，建立回归函数；对不同预测区域损失贫化率预测值按区域地质矿量加权，然后计算出整个矿山氧化矿、原生矿不同出矿截止含量对应的损失贫化率，进而回归出损失率、贫化率函数关系。

以整个矿区为例，根据矿石性质、矿体特征、损失率和贫化率历史数据统计，将整个矿区划分为8个区块，建立损失率与贫化率相关关系模型。在多种模型中，幂函数曲线回归模型拟合度最好。对多组原始数据组进行检查筛分、剔除异常数据，并进行加减标准差计算，最后再进行回归分析，得到最优的整体损失率和贫化率关系模型，如图2所示。

整个矿区的损失率、贫化率相关关系最优模型为

式中，S为损失率，%；P为贫化率，%。

用同样的回归分析法得出小区域回归方程。以采场-82 m 水平的一处预测区域为例，不同采矿方式形成不同的数学模型。

（1）下盘向上盘推进方式：

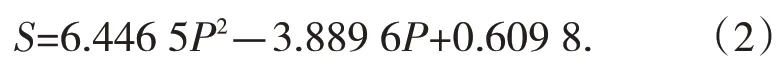
（2）沿走向推进方式：

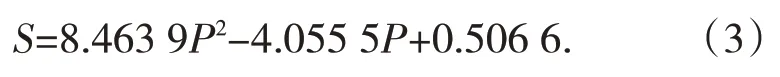
以上2种数学模型相关系数均在0.95以上，回归关系具有较高的可信性。

应用上述方程可以实现针对不同赋存特征区域和铲装推进方式，预测不同出矿截止品位下的损失贫化率，出矿截止品位的间距可根据需要进行设定。通过以上方法，实现对铲装环节的精细化管理，可以实现根据生产计划确定矿石品位目标，指定具体矿石品位计划，将矿石量和矿石品位具体落实到各作业地点，确保优化目标的实现。

2.3 技术经济优化模型的建立

对矿山生产成本和销售收入分析可得出模型目标函数，总利润为销售收入减去采矿、选矿、设备折旧费用及其他费用，则

2.4 优化模型求解程序

使用C#编程语言建立优化模型求解程序。在本程序中，将贫化率作为变量，根据成本参数和折现率，结合采出品位、精粉品位、精粉量、精粉售价等参数，对目标值总利润进行计算；每一方案都会得出相对应的总利润；如此往复循环，直到算完约束条件范围内的所有可行方案，然后以总利润最大值为评判标准，判定最优方案；当方案有效时，可以导出所有方案的数据表，将最优方案与现行和其他方案进行比较，计算出经营目标增量；最后将最优方案对应的参数值反馈给矿山，以供组织生产参考。

3 优化模型应用实例

3.1 参数的设定

本次数据采用矿山前几年的运营数据，工艺参数及成本部分参数如下。原矿采矿成本约为42.77元/t；吨原矿采矿维简费、资源税、安全生产费为31元/t 原矿；选矿加工费为41.79 元/t 原矿；固定资产折旧总额（含无形资产摊销）为900 000 万元；原矿管理费用及财务费用约为20 元/t；地质品位为29.18%；年原矿处理量为839 万t；生产剥采比平均值为3.2；选比平均值为3.3；精矿品位为64.3%；尾矿品位为10.5%；精矿售价为437.84 元/t。相应的约束条件为采出品位≥20%；贫化率、损失率波动范围为0～40%；精矿品位波动范围为±0.5%；产出精矿量≥矿山计划精矿量。

3.2 优化结果分析

依据上述参数及约束条件设定，利用优化模型求解程序，以矿山经济效益最大化为目标，进行模型规划求解。优化结果示例见表1、表2。

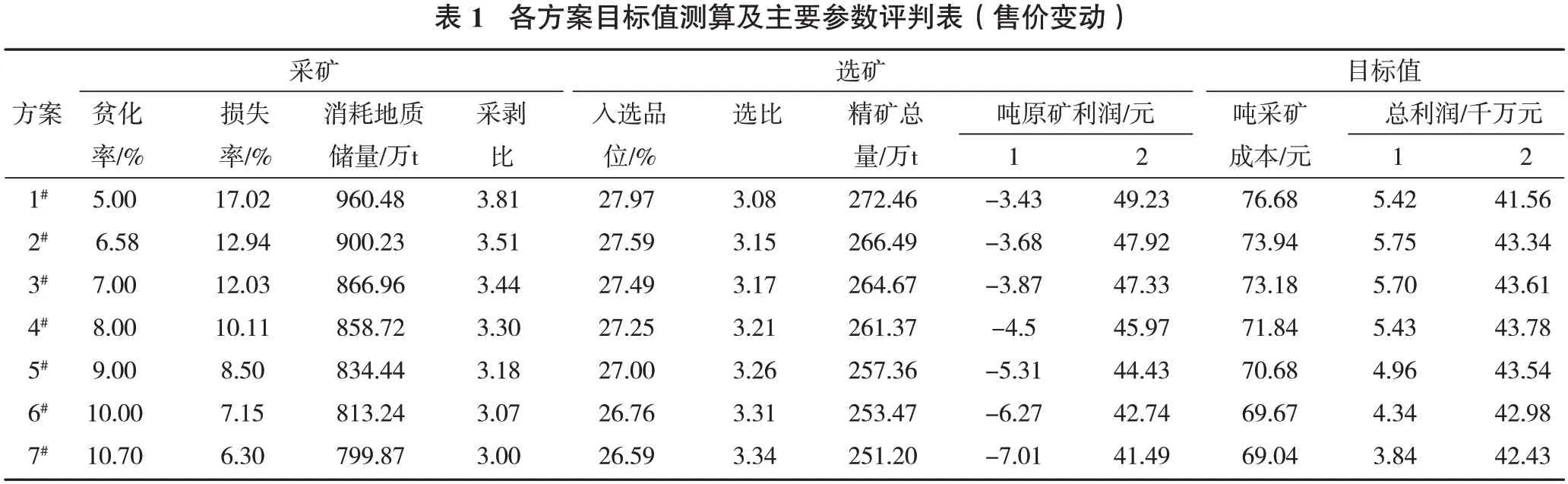
注：吨原矿利润中，1代表售价437.84元，2代表售价600元，总利润与之相对应。

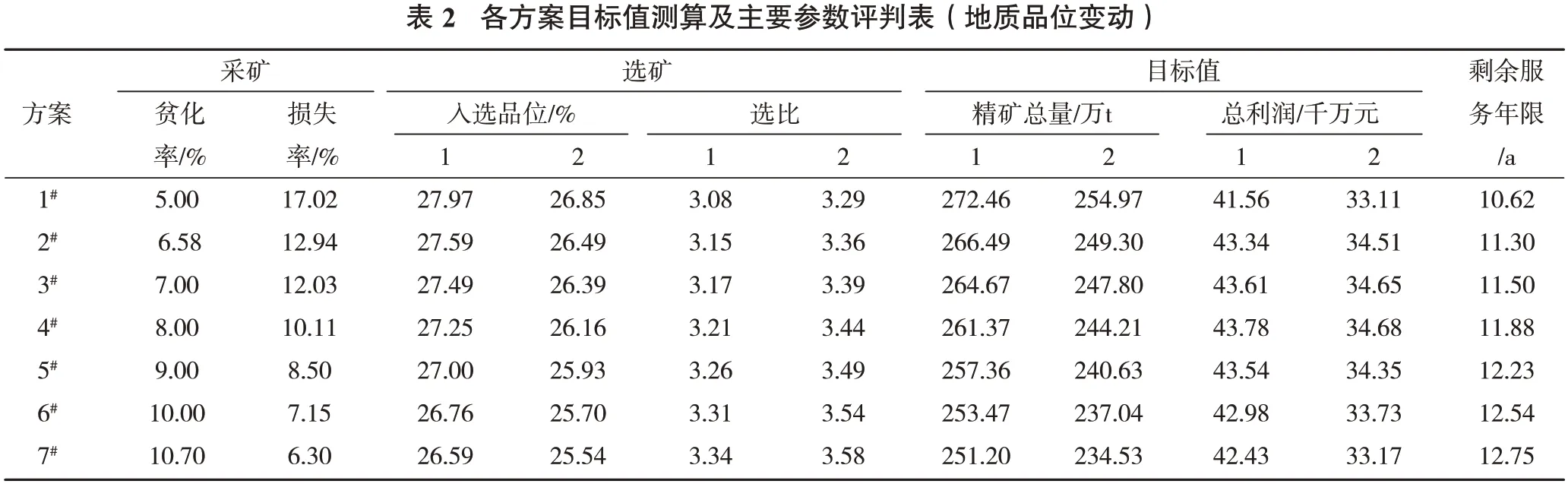
注：表中1代表平均地质品位为29.18%时的参数值，2代表平均地质品位为28%时的参数值。

3.2.1 不同售价

表1 中7#方案是目前矿山生产的实际贫化率，实际损失率为6.6%（多个月平均值），根据预测公式回归的损失率为6.3%，与实际值接近，计算矿山的年度总利润约为3.84千万元。当精矿售价不变的情况下，随着贫化率的调整，各参数发生变化，影响年度总利润。理论上在现有技术经济条件下，当调整至2号方案，贫化率为6.58%左右、损失率为12.9%左右时，矿山可获得更佳的经济效益，年度总利润为5.75 千万元，较未优化前贫化率为10.7%时的年度经济效益可增加约1.91 千万元。当市场情况好转，吨精矿售价由437.84元提升至600元时，应将各参数调整至4号方案，贫化率为8%左右、损失率为10.11%左右，才能实现利润最大化，较未优化前增加经济效益约1.35千万元。

3.2.2 不同地质品位

在当前技术条件下，即损失率为12.94%，贫化率为6.58%时，矿山剩余服务年限为11.30 a。在市场形势好转，吨精矿售价提升至600 元时，为了充分利用自然资源，延迟矿山服务年限，可以考虑降低地质品位。以表2 为例，将现行平均地质品位值由29.18%降为28%时，4 号方案仍为利润最大方案，虽然年度总利润降低8.96 千万元，但是矿山剩余服务年限增加0.58 a，以年度总利润为基础按比例计算，矿山整体利润将增加20.11千万元。

3.2.3 不同采矿成本、不同选矿加工费用

随着开采时间的增加，对矿山和矿石质量情况掌握的越来越精确，通过精细化管理，采矿成本与选矿加工费用将有所降低，但其只对年度总利润产生影响，不是影响损失率、贫化率选择的关键性因素。

4 结论

通过挖掘司家营北区实际生产数据，运用回归分析法、规划求解和C#语言编程，建立了以损失率、贫化率为重点的矿山相关指标的数学模型，构建了矿山技术经济指标体系优化模型。该模型符合司家营北区生产实际情况，明确了当市场变动、技术提升或地质条件变化时对技术经济指标的影响，为矿山技术经济指标的分配和调整提供了重要参考，对类似矿山的指标优化具有借鉴意义。