基于改进ACMPSO并行算法的土石坝本构参数反演

陈家琦, 岑威钧, 李邓军, 潘正阳

(河海大学水利水电学院，江苏 南京 210098)

为了评估土石坝的安全性，预测大坝的应力变形，需要获得土石料真实力学参数，为此常用现场试验和室内三轴试验[1-2]进行测试。但是，基于这类方法得到的参数计算得到的大坝应力变形与原位监测信息常有出入。为了准确计算和预测土石坝的应力变形，基于原位监测信息的参数反演成为获得坝体材料真实力学参数的有效方法[3]。

在岩土材料参数反演方面，不少学者引入了各种智能优化算法。张美英[4]采用免疫遗传算法对三峡茅坪溪沥青心墙坝进行了反分析，预测了大坝实际的运行性态；张丙印等[5]构造了基于人工神经网络和演化算法的位移反演分析方法，并采用该方法对三峡茅坪溪防护土石坝的变形进行了反演分析，验证了反演分析方法的有效性；贾陆锋等[6]将单纯形算法和模拟退火算法结合为一种混合优化算法，为反演地下工程围岩力学参数提供了有效途径；杜好[7]采用改进的单群体自适应微粒群算法对某面板堆石坝的4个邓肯E-B材料参数进行了反演分析，得到了比较合理的参数结果。此外，蚁群算法等其他优化方法在参数反演中也有不少应用[8-9]。

高维复杂岩土工程的材料参数反演问题通常存在最优解不唯一且计算量庞大的问题，常用优化算法容易陷入局部最优且计算效率十分低下。针对这类问题，本文对自适应混沌变异粒子群算法(adaptive chaotic mutation particle swarm optimization, ACMPSO)进行了改进，并采用改进的ACMPSO并行算法对某实际工程的面板堆石坝的4个材料分区共20个邓肯E-B材料参数进行了反演分析。

1 ACMPSO算法及其改进

1.1 ACMPSO算法

Kennedy等[10]根据鸟群觅食的行为提出了粒子群基本算法(particle swarm optimization,PSO)，该算法通过粒子种群间的相互指导和学习的方式来迭代寻找优化问题的全局最优解。ACMPSO是在PSO算法的基础上，引入了混沌序列和全局极值自适应变异策略，以改善PSO算法遍历性差、易于陷入局部最优等问题。

1.1.1混沌序列

混沌序列是指由某一初值和映射方程得到的一系列随机数，因其具有随机性、逻辑确定性、强敏感性、遍历性和不可预测性等特点，已被广泛运用于密码学当中。常用的混沌映射方程有Double-Bottom映射、Henon映射和Lorenz映射等[11]。

Yang等[12]对Double-Bottom映射进行了改进，构造出对初值敏感性更强的混沌映射，其表达式为

(1)

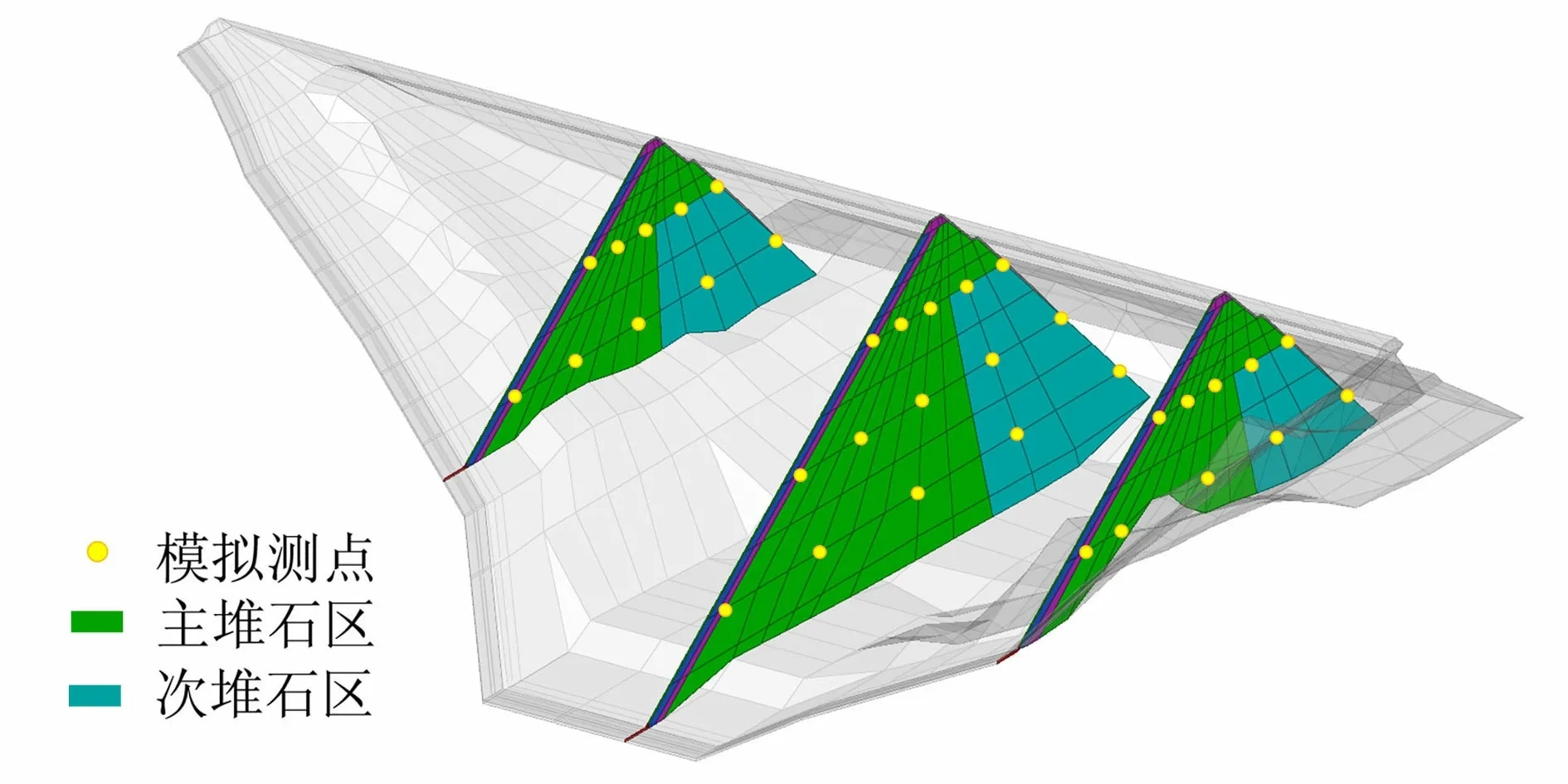
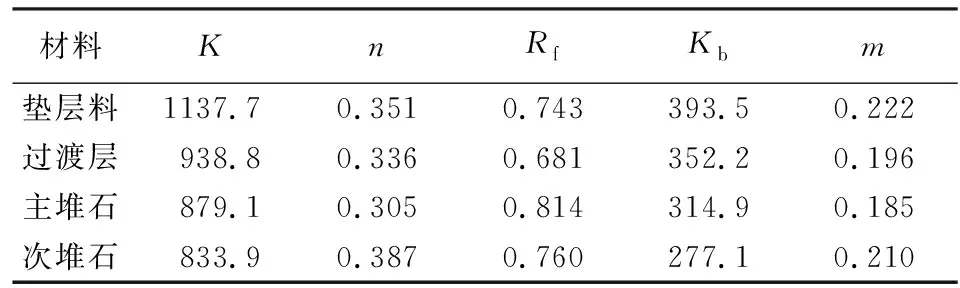
式中：rp为混沌序列第p个数。该映射在0

本文采用式(1)生成多条随机序列，用于PSO算法中粒子位置、速度的初始化，并代替速度更新公式中的随机数，保证种群在可行域内均匀分布，提高算法的搜索能力。

1.1.2 全局极值自适应变异策略

为了改善PSO算法易于陷入局部最优的问题，吕振肃等[13]引入了全局极值自适应变异策略，采用粒子群体适应度方差σ2反映粒子群体的收敛程度，当σ2小于某一阈值时，按某一概率对全局极值进行变异，全局极值第j维度的变异公式为

gbestj=gbestj(1+δω)

(2)

式中：gbestj为第j维度的全局极值；δ为变异系数，一般取0.5；ω为服从Gauss(0,1)分布的随机数。

1.2 改进的AMCPSO算法

1.2.1 全局极值自适应变异的改进

ACMPSO算法中，全局极值执行条件是粒子群体适应度方差σ2小于某一阈值，但是对于一些维度高、计算量大的材料参数反演问题，阈值敏感性很强，可能粒子群体还没有趋于收敛就会陷入局部最优，而这类问题的敏感性分析会耗费大量时间，这是不可取的。另一方面，变异公式(式(2))采用的是静态变异系数0.5，因此粒子所有维度具有统一的变异幅度和方向，对于某些粒子维度较高的复杂问题，统一的变异幅度和方向不一定适合于全局极值的所有维度，执行变异策略后全局极值的某些维度仍有可能处于边界附近，导致算法不能跳出局部最优或进入另一个局部最优。

针对上述问题，本文采用全局极值变异率Pm作为策略执行条件执行变异操作，虽然增加了算法的计算时间，但可以全程提高算法的全局搜索能力。在计算过程中，由于粒子迭代的位置是随机的，很可能一部分粒子会停留在可行域的边界附近，一部分粒子停留在可行域的中心，那么对于靠近可行域边界的粒子，变异幅度应该较大；靠近可行域中心的粒子，变异幅度应该较小。因此，采用动态变异系数要比静态变异系数更具有普适性，使粒子的各维度都得到最合适的变异幅度。全局极值第j维度的动态变异系数δbestj表达式为

(3)

式中：uj、lj分别为可行域第j维度的上界和下界；τ为最小扰动系数，0<τ<1；μ为控制系数，1<μ<2。

为了引导全局极值朝着正确的方向变异，采用如下改进的变异公式：

gbestj=gbestj[1+ψ(gbestj)δbestj|ω|]

(4)

1.2.2粒子位置自适应变异

为了提高PSO算法前期的局部搜索能力，加快收敛速度，借鉴遗传算法的变异思想[14]，引入动态变异函数控制粒子位置变异，在算法前期，变异率较高，之后随着迭代次数的增加逐步降低。动态变异函数V(t)为

V(t)=V0[1-(t/tmax)α]β

(5)

式中：V0为初始变异率；t为当前迭代次数；tmax为最大迭代次数；α、β为控制参数，一般取α=1.7，β=10。

在动态变异函数控制下，算法初期会筛选较多的粒子进行变异，扩大粒子在可行域内搜索范围，加快了算法的收敛速度；在算法中后期，变异的粒子数量逐渐降低，防止粒子异常波动影响算法的收敛能力。

变异粒子i的第j维度的动态变异系数δij为

(6)

式中：zij为变异粒子i的第j维度的位置。

根据变异控制函数选择出需要变异的粒子后，对变异粒子的位置进行变异，变异粒子i的第j维度的粒子位置变异公式为

zij=zij[1+ψ(zij)δij|ω|]

(7)

1.2.3并行计算

采用Fortran语言编写PSO、ACMPSO和改进的ACMPSO算法，将生成的各粒子参数组写为材料文件，利用批处理文件间接调用ADINA软件读取材料文件，进行有限元计算和后处理[15]。由于对每个粒子进行的有限元计算是相互独立的，因此可以在反演程序中插入并行指令进行并行计算。

共享内存编程应用程序接口的工业标准协议(OpenMP)为一种多线程的程序设计指令，可以在已编写的Fortran程序段内以标识符的方式添加并行指令，用于指示Fortran程序开始和结束多线程运行的时间和地址[16-17]。为了防止多线程运行可能引起的文件读写冲突，反演算法选用了OpenMP Fortran API中具有独立计算区域的Sections并行指令。

1.3 算法验证

为了验证改进的ACMPSO并行算法的合理性，以某面板堆石坝为例，布置35个模拟测点，有限元网格模型及测点布置如图1所示，堆石料本构模型采用邓肯E-B模型[18-19]，对坝体主堆石和次堆石的切线弹性模量参数K、n以及切线体积模量参数Kb进行反演计算。算法验证中，参数浮动范围为准确值的±50%，模拟实测值为有限元正算得到的竣工期坝体沉降，目标函数公式为

(8)

图1 面板坝算例有限元网格模型及测点布置

分别采用PSO算法、ACMPSO算法和改进的ACMPSO并行算法对面板坝算例进行参数反演，各算法参数均设置为：种群数量M=4，初始变异率V0=0.5，全局极值变异率Pm=0.5，惯性因子w最大值、最小值分别为0.9和0.1，最小扰动系数τ=0.1，控制系数μ=1.5，固定初始粒子位置和参数浮动范围，3种算法的目标函数迭代过程曲线如图2所示。

图2 不同算法迭代过程曲线对比

由图2可以看出，PSO算法的收敛速度很慢，在迭代15次之后陷入了局部最优，难以跳出；ACMPSO算法的收敛速度与PSO算法大致相同，但是在第6次迭代时跳出了局部最优，目标函数值大幅下降，随后算法再次陷入局部最优，说明ACMPSO算法不能有效避免算法陷入局部最优，不适用于高维度的材料参数反演；改进的ACMPSO并行算法收敛速度很快，迭代10次后，目标函数值降幅已达总降幅的90%以上，中后期算法没有陷入局部最优，目标函数值呈下降趋势，最终收敛至0.75%，说明改进的ACMPSO并行算法前期局部搜索能力强、后期全局搜索能力强，在高维度的材料参数反演中能够有效地避免算法陷入局部最优。

2 实例验证

2.1 工程概况

某面板堆石坝坝顶高程757.0 m，最大坝高143.0 m，坝顶长度460.0 m。坝体上游坝坡1∶1.5，下游坝坡1∶1.3。坝0+261.0 m断面处布置有3层水管式沉降仪，高程分别为650.0 m、687.8 m和721.7 m，共18个测点。通过对测点实测值的分析整理，发现ES3-3和ES3-7沉降仪损坏，ES1-3、ES1-4、ES3-6和ES3-8沉降仪测值异常，反演分析时剔除，其余12个测点作为本文反演分析参考点。沉降仪布置及实测结果如图3所示。

图3 坝0+261.00 m断面沉降仪布置及实测结果(高程单位：m；沉降单位：cm)

根据大坝实际填筑方式，划分大坝三维有限元计算网格，大坝网格共有7 026个节点，6 610个单元，坝体实际测点分布见图4。

图4 坝体实际测点布置

2.2 反演参数选取与设置

坝体填筑料主要包括垫层料、过渡层、主堆石和次堆石。E-B模型共有9个参数，其中初始内摩擦角φ、内摩擦角增量Δφ和土体黏聚力c一般可由试验确定，卸载弹性模量参数Kur的敏感性很低，可不用反演，因此将切线弹性模量参数K、n，破坏比Rf和切线体积模量参数Kb、m作为待反演参数，参考现场试验数据和类似的工程经验，拟定了坝体材料待反演参数的取值范围以及其余参数的取值如表1所示。

表1 筑坝料E-B模型参数

由于反演分析共有20个待反演参数，且部分待反演参数的敏感性较低，需要适当扩大迭代次数和粒子种群数，算法参数设置为：粒子种群数M=8，初始变异率V0=0.8，全局极值变异率Pm=0.7，最小扰动系数τ=0.4，最大并行线程数为4，其余参数均与1.3节一致。为了确保反演结果的可靠性和稳定性，一般需要在相同条件下进行多次(不少于3次)独立的反演计算，计算的次数视反演计算量的大小而定，最终反演结果应取为多次独立反演计算结果的平均值。

2.3 反演结果分析

在相同条件下进行3次独立的参数反演计算，得到的迭代过程曲线如图5所示。由图5可知，3次反演计算的迭代过程比较相近，迭代计算5次后，目标函数值降幅可以达到7%，占总降幅的一半以上，再次说明改进的ACMPSO并行算法收敛速度很快，最终经过50次迭代计算，目标函数的平均值低于5%，满足工程误差限。

图5 3次参数反演计算的迭代过程曲线

表2给出了各材料参数反演结果的平均值，可以看出反演计算得到的参数均比较合理，符合一般规律，且3次反演的参数结果没有出现异常波动，说明改进的ACMPSO并行算法稳定性好，能够得到合理的反演结果。

表2 3次参数反演结果的平均值

图6给出了坝0+261.00 m监测断面上有效测点的实测沉降和反演沉降(3次反演计算沉降的平均值)的分布对比，可以看出，坝体实测沉降与反演计算的沉降吻合度很高，计算结果符合面板堆石坝的沉降分布规律，测点沉降的平均相对误差为4.6%，最大相对误差为10.7%，位于ES3-1测点，说明改进的ACMPSO并行算法具有较高的搜索精度，能够处理高维度、计算量庞大的参数反演问题。

图6 坝0+261.00 m断面竣工期实测沉降与反演沉降分布对比(高程单位：m；沉降单位：cm)

3次反演计算的平均时长为9.26 h，而单线程的反演计算则需要28.43 h，并行计算的平均加速比为3.07，并行效率为77%。若提高最大并行线程数和计算机性能，加速比可以继续提高，但并行效率会降低。

3 结 论

a.改进的ACMPSO并行算法融合了新的混沌映射和全局极值变异策略，引入了粒子位置变异策略和并行算法。与PSO算法和ACMPSO算法相比，改进的ACMPSO并行算法具有收敛速度快，能有效避免算法陷入局部最优等特点。

b.将改进的ACMPSO并行算法应用于某面板堆石坝筑坝材料的参数反演中，3次独立反演计算的迭代过程比较相近，监测点沉降的平均相对误差为4.6%；利用反演值得到的坝体变形与原位监测量匹配度高，合理反映了坝体实际的变形情况；并行计算的平均加速比为3.07，说明改进算法稳定性好，搜索精度高，能够大幅提升计算效率，为处理高维度、计算量庞大的复杂参数反演问题提供了一个可行的方法。