基于动态矩阵控制的DAB变换器电流应力与回流功率优化方法
杨向真,孔令浩,杜 燕,苏建徽
(1.合肥工业大学电气与自动化工程学院,安徽省合肥市 230009;2.光伏系统教育部工程研究中心(合肥工业大学),安徽省合肥市 230009)
0 引言
双有源桥(dual active bridge,DAB)变换器拓扑具有电气隔离、双向功率传输和宽升压降压比等优点[1],在众多功率转换装置中得到了广泛应用[2],如在交直流混合微电网[3]、微电网储能系统[4]、电动汽车[5]等系统中都得到了应用。
相移控制是DAB变换器的主流控制方法。传统的单相移(single-phase-shift,SPS)控制因具有较高的动态性能、易于实现软开关控制、控制方式简单等特点[6-7]得到了广泛应用。SPS控制在空载和轻载时变换器回流功率较大,当传输功率一定时,回流功率越大,所需正向传递的功率也越大,不仅导致变换器效率下降[7],也对功率器件有更高的要求。而且SPS控制中,当电压传输比偏离1时,会使电感电流增长加快,增大电流应力,导致电感磁芯失磁[8]。因此,DAB变换器在非额定工况下工作时,系统效率下降。为了避免传统SPS控制的缺点,文献[9]提出了在双相移(dual-phase-shift,DPS)控制下的最小电流应力优化方法。文献[10-11]在DPS控制的基础上进一步增加控制自由度,提出三重相移(triple-phase-shift,TPS)控制下的最小电流应力优化策略。文献[12]提出了在扩展相移(extendedphase-shift,EPS)控制下的最小回流功率优化策略。文献[13]提出在DPS控制下的最小回流功率优化策略。
DAB变换器的电压控制方面,传统单电压闭环控制通过比例-积分(PI)控制器来实现,在不同负载、输入电压变化等情况下的动态适应性较差。为了提高变换器动态性能,文献[14]提出负载电流前馈控制方法,该方法不需要电感等电路参数参与控制,这增加了控制方法的兼容性和可移植性。文献[15]提出的直接功率控制算法能有效提高输出电压的动态性能,减小输入电压扰动对输出电压的影响。文献[16]结合直接功率控制与前馈控制策略,提出了一个虚拟的直接功率控制,对负载或输入电压、电压波动和启动阶段的输出电压进行快速瞬态响应。上述文献所提出的控制策略都含有PI控制环节,这使得在对动态要求较高的系统中不能满足控制要求,PI参数整定也没有规范的界定。文献[17]使用模型预测控制,通过建立DAB变换器输出电压状态空间平均化模型,在输入电压波动和负载扰动条件下,预测了下一时间段输出电压的动态特性。文献[18]将动态矩阵控制(dynamic matrix control,DMC)运用在DAB变换器的控制上,提高了系统的动态特性和鲁棒性,但并未解决DAB变换器采用SPS控制时存在的回流功率和电流应力较大等问题。
本文首先分析了DPS控制下DAB变换器的2种工作模式,以及各自的电流应力和回流功率;然后,建立了抑制电流应力和回流功率的双目标权重优化函数,求解出条件最优解,并设定了双目标权重优化函数中加权因子的选取原则。之后,为了提高系统的动态响应性能和鲁棒性,本文提出并详细介绍了基于DMC的DAB变换器电压预测控制方法。最后,基于硬件在环仿真实验平台,验证了所提电压预测控制和双目标权重优化方法的有效性。
1 DPS控制
图1为DAB变换器的拓扑结构,该拓扑由2个对称的H桥通过高频变压器连接而成,从而形成三级结构:高频逆变输入级、隔离级和整流输出级。Vi和Vo分别为DAB变换器输入和输出电压;Ci和Co分别为输入侧支撑电容和输出侧滤波电容;L为辅助电感;变压器变比为n∶1;Vab和Vcd分别为逆变桥输出电压和整流桥输入电压;R为负载电阻。
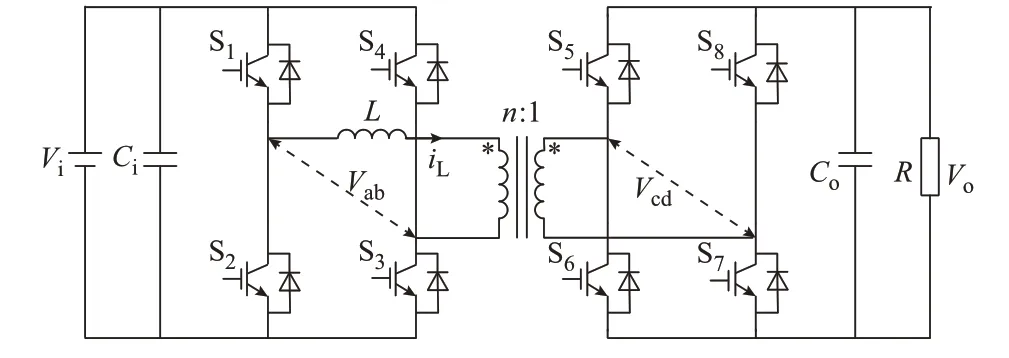
图1 DAB变换器拓扑Fig.1 Topology of DAB converter
相比于传统的SPS控制,DPS控制在两侧H桥增加了内移相比,使得控制的灵活度得以提升。外移相比D2调节功率流的方向和大小,当D2≥0时功率正向流动,当D2<0时功率逆向流动。本文仅考虑功率正向流动的情况即D2≥0。根据内移相比D1和外移相比D2的大小可以将DPS控制下的DAB变换器分为2种工作模式:0≤D1≤D2≤1和0≤D2≤D1≤1。
当0≤D1≤D2≤1时,假 定 电 压 传 输 比kv≥1,kv=Vi/(nVo)。当变换器稳定工作后电感电 流 满 足iL(t)=-iL(t+TS),其 中2TS=1/f,TS为半个开关周期,f为DAB变换器开关频率。附录A图A1(a)为0≤D1≤D2≤1时DAB变换器的主要波形,由文献[9]可知传输功率和电流应力为:
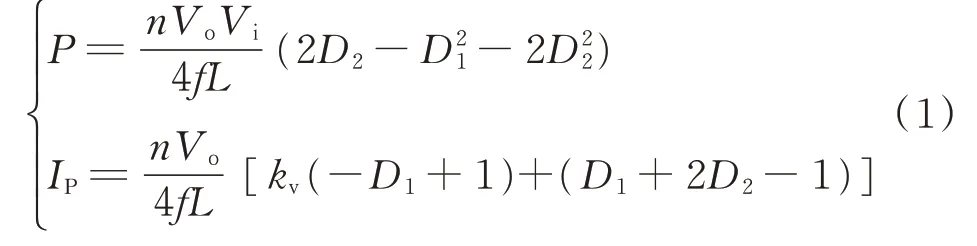
如附录A图A1(a)黄色部分所示,电感电流iL(t)与逆变输出级输出电压Vab方向相反,功率向输入侧回流,定义为回流功率。而传输功率P=Pi-PM(其中Pi为输入侧电源的正向传递功率,PM为回流功率),可以看出当传输功率P一定时,回流功率越大,所需正向传递的功率也越大,这不仅会导致变换器效率下降,同时也会对功率器件有更高的电气性能要求[7]。可见,减小回流功率是DAB变换器控制的一个重要目标。得到0≤D1≤D2≤1时的回流功率为:

附录A图A1(b)为0≤D2≤D1≤1时DAB变换器的主要波形,其传输功率、电流应力和回流功率为[11]:

2 双目标权重优化
为了同时实现减小回流功率和电流应力2个优化目标,减小DAB变换器的传输损耗,提高系统效率,这里通过构建权重优化函数[19-20],求解出移相比的条件最优解。
2.1 移相比为0≤D1≤D2≤1时
1)构建权重优化函数
权重优化函数为:

式中:ω1为0≤D1≤D2≤1时电流应力的加权因子,回流功率的加权因子为1-ω1。
约束条件为:
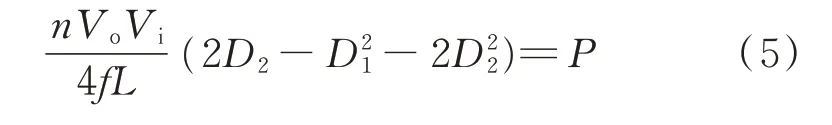
2)无量纲化
这里涉及电流应力、传输功率和回流功率3个量,对这3个量进行无量纲化,无量纲化处理方法为:
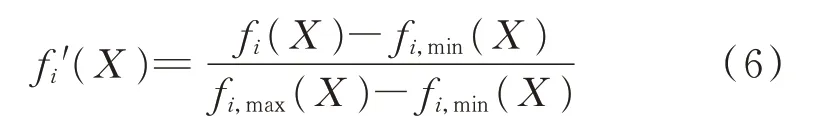
式中:fi,max(X)、fi,min(X)分别为变量fi(X)在约束条件下的最大值和最小值。
DPS控制下电流应力、传输功率和回流功率的最大值,以及在理想状态下kv=1时得到的电流应力、传输功率和回流功率3个量的最小值为:
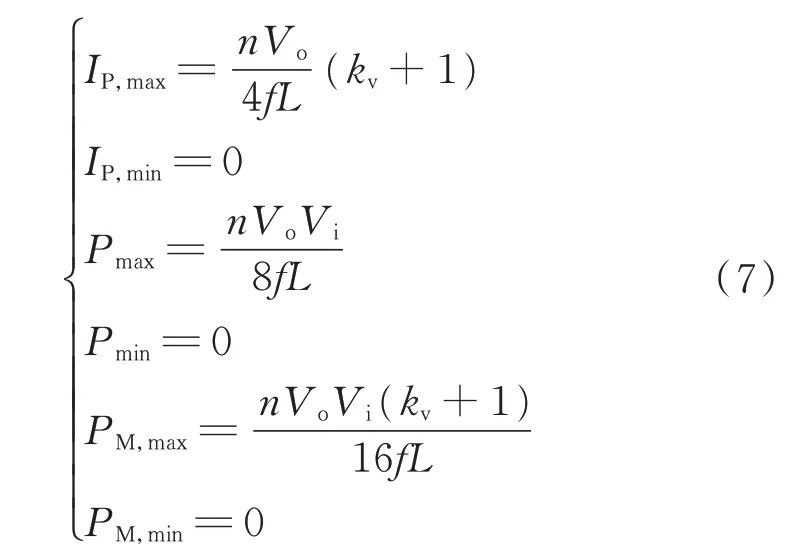
根据式(6)所示的无量纲化公式,结合式(1)、式(2)和式(7)可得到电流应力、传输功率和回流功率的无量纲值为:
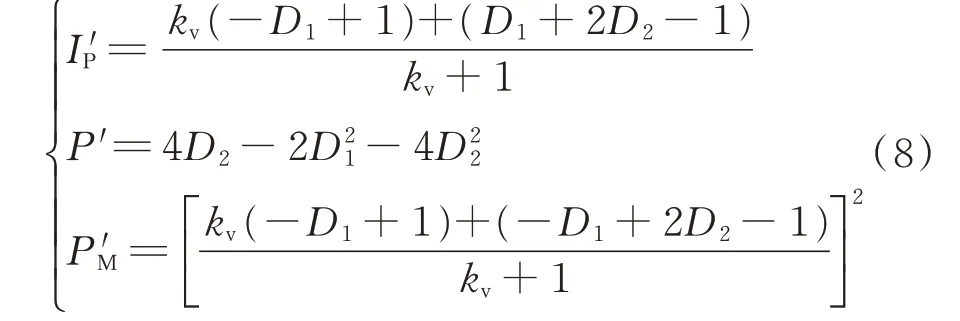
由 式(1)可 得kv(-D1+1)+(-D1+2D2-1)≥0,则{[kv(-D1+1)+(-D1+2D2-1)]/(kv+1)}2的条件最优解与[kv(-D1+1)+(-D1+2D2-1)]/(kv+1)的条件最优解相同,为了降低求解难度可直接求解[kv(-D1+1)+(-D1+2D2-1)]/(kv+1)的条件最优解。
3)计算移相比条件最优解
上文分析得到了DAB变换器的双目标权重优化函数和约束条件。在高等数学中,拉格朗日乘子法是求解等式约束下优化问题的有效方法[8-9]。列写拉格朗日函数为:
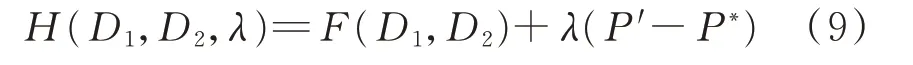
式中:P*为期望的传输功率值;λ为拉格朗日乘子。
为了获得多目标函数的条件最优解与优化移相比D1和D2之间的关系,对函数求导,可得:
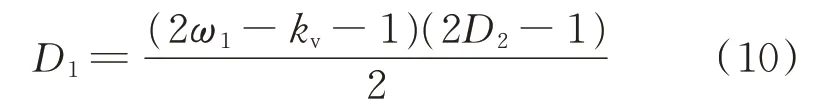
令C1=(2ω1-kv-1)/2,则D1=(2D2-1)C1。将D1代入式(8)可得:
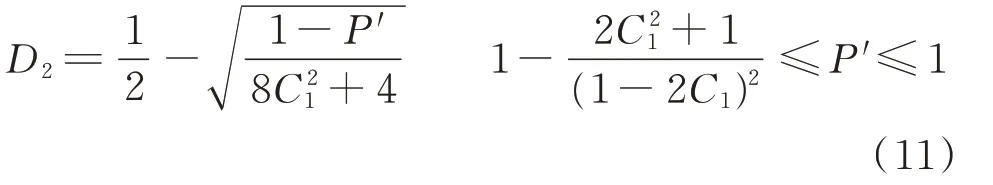
将D1和D2的值代入式(1)、式(2)可求得移相比为0≤D1≤D2≤1时的电流应力IP和回流功率PM,可得IP是关于电压传输比kv、传输功率P′和加权因子ω1的函数,即IP(kv,P′,ω1)。
2.2 移相比为0≤D2≤D1≤1时
DAB变换器工作在移相比为0≤D2≤D1≤1时的讨论过程和0≤D1≤D2≤1时一样,为了缩减篇幅,直接给出电流应力、传输功率和回流功率的无量纲值,如式(12)所示:

列写拉格朗日函数,求得优化移相比D1和D2之间的关系:
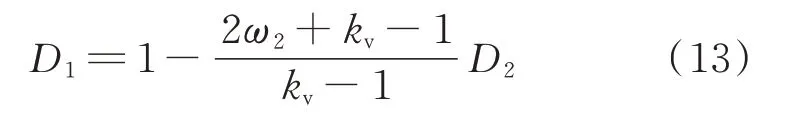
式 中:ω2为0≤D2≤D1≤1时 电 流 应 力 的 加 权因子。
令C2=(2ω2+kv-1)/(kv-1),则D1=1-C2D2,代入式(12)可得:

将D1和D2的值代入式(3)可求得移相比为0≤D2≤D1≤1时的电流应力IP和回流功率PM,可得IP是关于电压传输比kv、传输功率P′和加权因子ω2的函数,即IP(kv,P′,ω2)。
2.3 确定加权因子
文献[9]所提出的DAB变换器在DPS控制下的优化是以电流应力优化为目标,以传输功率为约束条件,通过列写拉格朗日函数求解得到电流应力最小值,没有对回流功率进行优化,为了和本文的双目标权重优化方法进行区分,将其称为单电流应力优化。2种工作模式下的移相比D1、D2值如下。
0≤D1≤D2≤1时:

将D1和D2代入2种工作模式下的电流应力和回流功率公式(式(1)、式(2)和式(3)),可以求得单电流应力优化2种模式下的电流应力IP-S、回流功率PM-S。可得IP-S是关于电压传输比kv和传输功率P′的函数,即IP-S(kv,P′)。
下面阐述双目标权重优化控制方案中加权因子的影响和确定原则。当0≤D2≤D1≤1时,在相同电压传输比kv和传输功率P′的条件下,随着ω1从0增大到1,双目标权重优化方法将不断加强对电流应力的优化能力,而逐渐削弱回流功率的抑制效果,也就是说在双目标权重优化控制下,电流应力将会大于单电流应力优化方法下的稳态值IP-S;ω1越小,电流应力抑制效果越差。因此,权重优化函数中加权因子ω1的选取原则为:不过分增大DAB变换器电流应力的同时尽量减小回流功率。
令电流应力比Ri=IP/IP-S,则Ri是关于电压传输 比kv、传 输 功 率P′和 加 权 因 子ω1的 函 数,即Ri(kv,P′,ω1)。画出在不同加权因子ω1情况下,Ri随电压传输比kv和传输功率P′变化的三维图,如图2(a)所示。从图2(a)可以看出,在传输功率固定的情况下,随着传输比kv的减小,电流应力比Ri增大,且加权因子ω1越小,Ri越大;传输比kv固定时,双目标权重优化控制对轻载的电流应力抑制效果比重载时差,且随着加权因子ω1的减小,Ri增大。因此,为了保证较好的电流应力抑制效果,以轻载时双目标权重优化抑制效果最差点小于设定值为选取ω1的基 准。例 如 约 定Ri≤1.01为 基 准,则 图2(a)中ω1=0.95时DAB变换器满足在各种电压传输比kv和传输功率P′变化范围内始终保证Ri≤1.01,实际系统也可以根据需要合理选取ω1设定值。
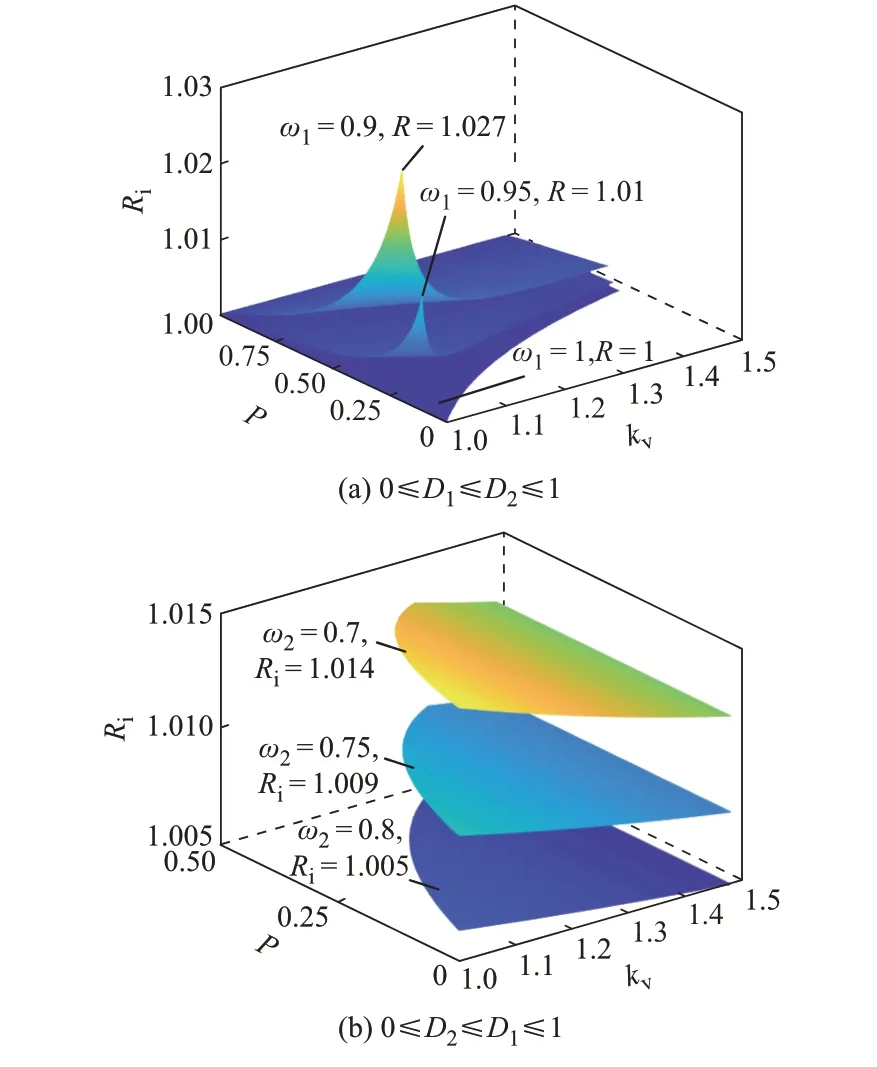
图2 电流应力比随加权因子、电压传输比和传输功率的变化曲线Fig.2 Curves of current stress ratio varied with weighting factor,voltage transmission ratio and transmission power
同理,当移相比0≤D2≤D1≤1,参考上文移相比0≤D1≤D2≤1时加权因子的选取方法,假设选定Ri≤1.01为优化基准。如图2(b)所示,为了能够满足Ri≤1.01的要求,则需要ω2≥0.75,故可以取ω2=0.75作为第2种工作模式的加权因子。
将得到的加权因子代入回流功率公式中,得到双目标权重优化控制下的回流功率,并与单电流应力优化下产生的回流功率作对比,令RPM=PM/PM-S,绘制出回流功率比RPM随电压传输比和传输功率的变化曲线,如附录A图A2所示。从图A2中可以看出,2种工作模式下都能取得较好的回流功率优化效果。
3 DMC方法
DAB变换器通常采用基于PI控制的电压闭环控制方法使输出电压达到给定值。该方法简单、有效,但属于滞后控制,且在负载、输入电压变化等情况下的动态适应性较差,PI参数也难以整定。DMC算法的独特性在于采用易于测量的受控对象的阶跃响应来建模,适用于渐进稳定的线性对象,具有算法简单、鲁棒性强等特点。DMC算法包括预测模型、滚动优化和误差反馈矫正3个部分。
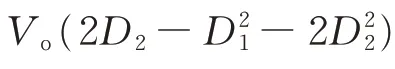
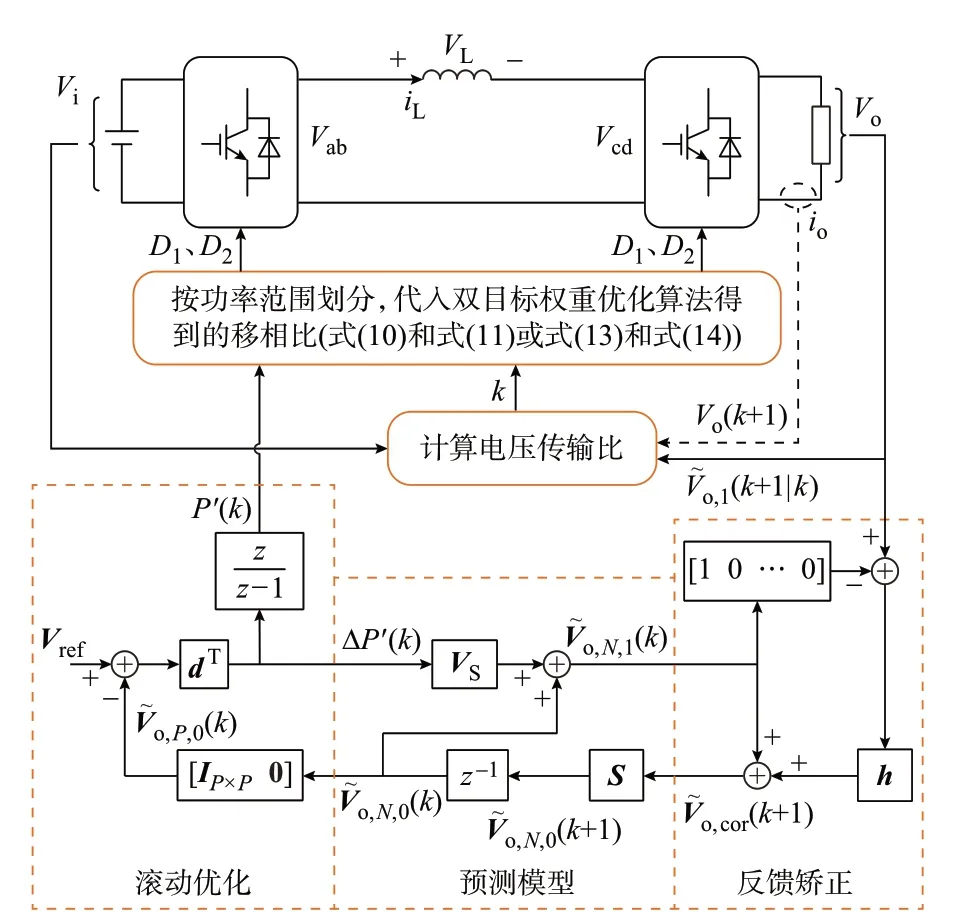
图3 DAB变换器控制框图Fig.3 Control block diagram of DAB converter
3.1 预测模型
在DMC中,首先需要获得DAB变换器的阶跃响应采样值[21]。如附录A图A3所示,给DAB变换器施加P′=0.1时对应的移相比输入信号,得到输出电压Vo的响应曲线。并用输出电压阶跃响应采样值组成的有限集合{V1,V2,…,VN}来描述DAB变换器的动态特性,把向量VS=[V1,V2,…,VN]T称为模型向量,N称为建模时域。
根据P′=0.1阶跃输入情况下DAB变换器输出电压Vo的模型向量VS=[V1,V2,…,VN]T,由线性系统的比例和叠加特性可知[22],在k时刻给DAB变换器一个输入增量ΔP′(k),则可以用已经获得的模型向量对未来k+i时刻的电压输出值进行预测。则当k时刻有M个(M称为控制时域)连续的控制增量ΔP′(k),ΔP′(k+1),…,ΔP′(k+M-1)作用于DAB变换器,得到未来k+i时刻的预测输出电压值 为:
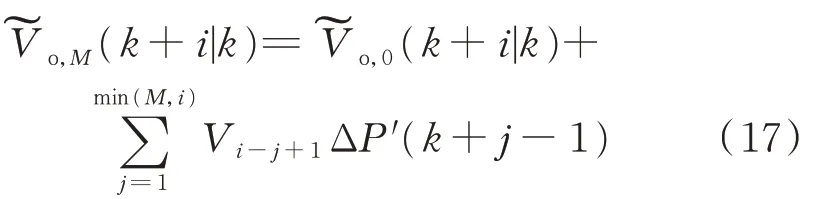

3.2 滚动优化

式 中 :Q=diag[Q1Q2…QP]和R=diag[R1R2…RM]分别为误差权矩阵和控制权矩阵。
使J(k)取极小值的必要条件为dJ(k)/dΔP′M(k)=0,可 求 得M个 最 优 功 率 控 制 增 量ΔP′(k),ΔP′(k+1),…,ΔP′(k+M-1),结 果 如式(20)所示:
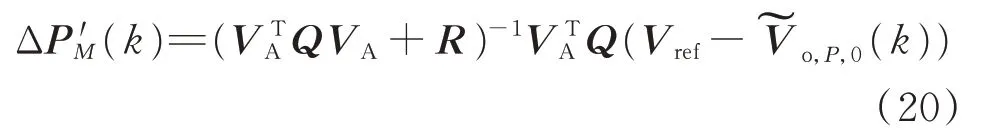
取第一项ΔP′(k)作为即时控制增量,可表示为:

式中:M维向量cT=[1 0…0]。
在求出功率控制增量ΔP′(k)后,实际采取的功率控制量为:
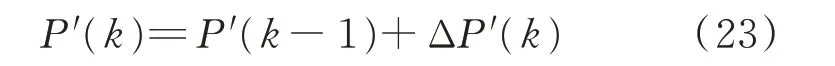
3.3 反馈矫正
由于获得的DAB变换器模型向量参数不一定准确,且当系统有干扰时,预测得到的输出电压值与实际输出值存在误差,需要对电压预测值进行矫正,从而更加接近期望输出电压轨迹,并且达到闭环控制的效果。根据k时刻的预测初值和功率增量ΔP′(k)的输入作用效果,得到k时刻的电压输出预测值为:

4 实验结果及分析
为了验证在本文所提控制策略作用下,DAB变换器输出电压动态响应性能以及对电流应力和回流功率的抑制效果,在以DSP芯片TMS320F28335为核心控制的StarSim平台上进行验证,DMC算法相关参数如附录A表A1所示,DAB变换器主要参数如附录A表A2所示。
4.1 动态性能验证
为了对比DAB变换器在DMC和PI这2种控制作用下的电压动态响应性能,对比对象为文献[16]提出的虚拟直接功率控制(virtualdirect power control,VDPC),下 面 分 别 进 行 了DAB变 换 器 启动、负载突变、输入电压突变以及输出电压参考值突变4组实验。
图4(a)为负载电阻为6Ω时DAB变换器在2种控制方式下输出电压和电感电流的启动波形,输出电压参考值为150 V,可以看出,DMC下的输出电压在7 ms内快速达到指定的参考值,且无超调量。VDPC下输出电压在9 ms时达到稳态值。因此,DMC下DAB变换器具有更好的启动性能。
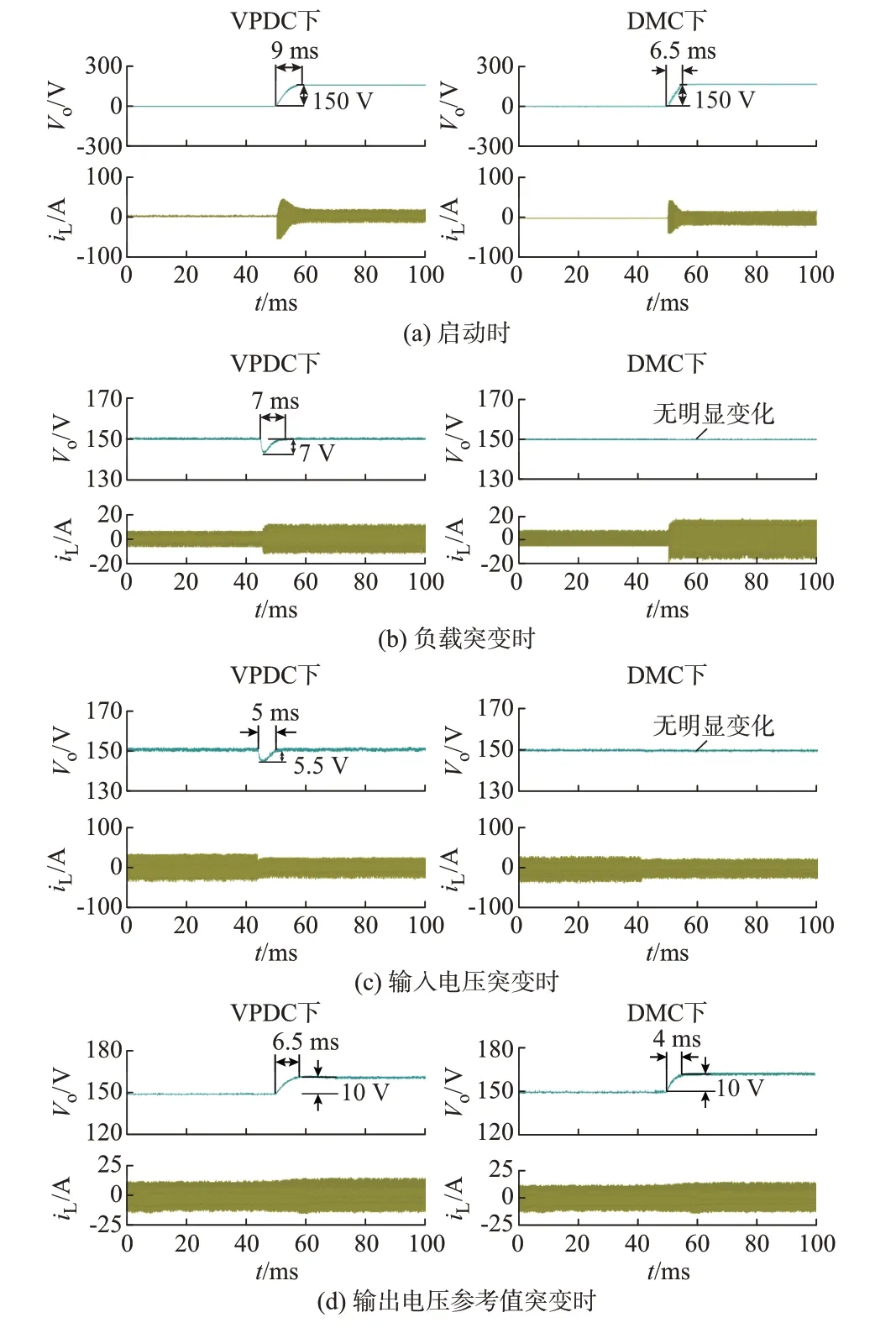
图4 输出电压和电感电流动态响应实验波形Fig.4 Experimental waveforms of dynamic response of output voltage and inductor current
图4(b)为当负载电阻由8Ω突变为4Ω时的实验波形,可以看出DMC下的DAB变换器输出电压无明显的变化,而在VDPC下输出电压在跌落7 V后需要7 ms才达到稳态值。
DAB变换器输入电压由450 V跌落到350 V时的电压波形如图4(c)所示,DMC下的DAB变换器输出电压无明显波动,而VDPC下的DAB变换器输出电压波动5.5 V后需要5 ms才能进入稳态。
图4(d)为输出电压参考值由150 V变为160 V时,DMC下DAB变换器输出电压在4 ms内达到稳态,而VDPC下需要6.5 ms才能使DAB变换器输出电压达到稳态。
从DAB变换器的启动过程、负载突变、输入电压变化和输出电压参考值突变4个实验可以得出如下结论:在DMC下的DAB变换器相比PI电压闭环VDPC下的DAB变换器有更快的响应速度,在动态调整时输出电压的波动较小,有较好的鲁棒性。
4.2 双目标权重优化效果验证
下面对比本文所提双目标权重优化控制和文献[9]所提单电流应力优化控制对电流应力和回流功率的抑制效果,两者均在DMC下完成。图5为负载为4Ω时的单电流应力优化波形、双目标权重优化波形以及输出电压对比波形。从图5(a)和(b)中可以看出,在负载为4Ω时2种优化方案下的电流应力均接近18.2 A,可以认为2种优化方案有相同的电流应力优化效果。图5(a)和(b)中红色面积部分为回流功率PM,可以很明显看出在单电流应力优化下回流功率较大,双目标权重优化下系统在稳定后回流功率减小了近40%,以至于在一个脉宽调制(PWM)周期内传输相同的功率时,单电流优化方案需要传输更多的正向功率,从而造成系统效率下降。
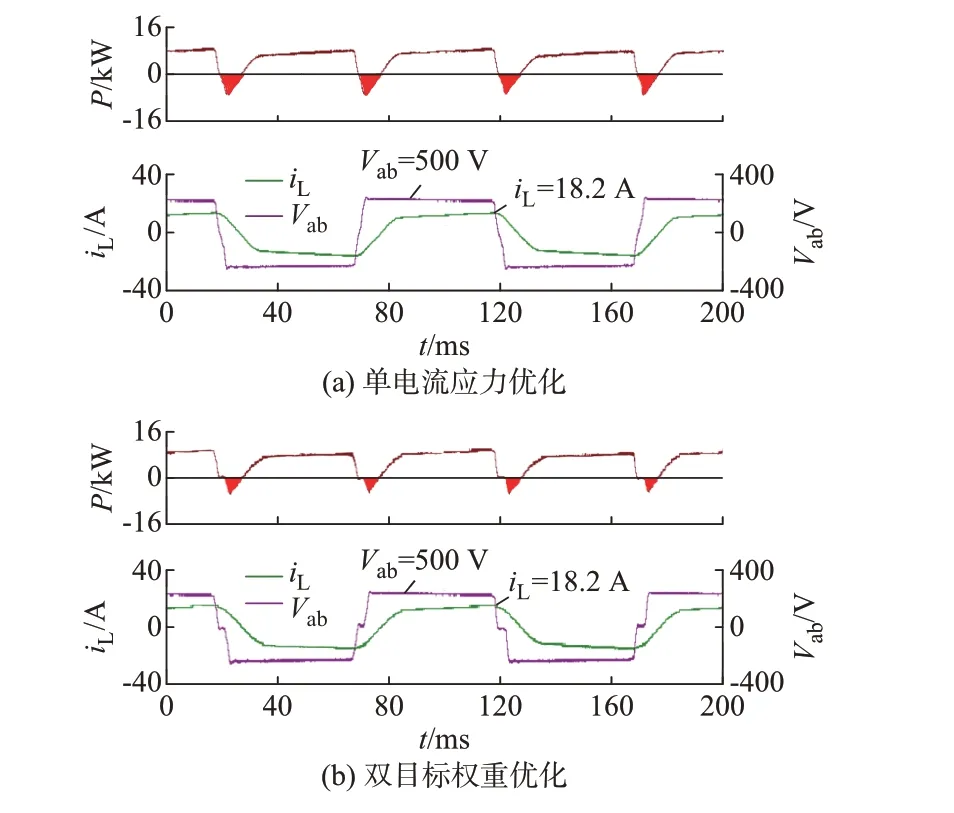
图5 负载为4Ω时的实验波形Fig.5 Experimental waveforms when load is 4Ω
附录A图A4为10Ω负载时的实验波形。图A4(a)和(b)分别为电感电流iL、桥臂侧输出电压Vab、瞬时功率P的波形,可见系统稳定后双目标权重优化和单电流应力优化下的电流应力均接近8.1 A,可以认为2种优化方案有相同的电流应力优化效果。同时,图A4(a)和(b)中红色面积部分显示双目标权重优化下的回流功率要远远小于单电流应力优化下的回流功率,系统稳定后回流功率减小了近50%,这样大大提高了系统的效率。
5 结语
为了实现提高电压动态响应速度的同时抑制电流应力和回流功率,本文提出了一种DMC电压预测控制和双目标权重优化控制相结合的DAB变换器控制策略,优化选取了多目标优化控制中的加权因子。通过实验验证得到以下结论:
1)和DMC相比,VDPC在DAB变换器启动、负载突变、输入电压突变和输出电压参考值突变时DAB变换器的响应时间较长,电压波动幅度大。相比之下DMC有快速瞬态响应特性,在动态调整时输出电压的波动较小,大大提高了系统的动态响应速度和系统的鲁棒性。
2)和单电流应力优化相比,双目标权重优化在达到同样的电流应力优化效果的同时,回流功率大幅度减小,大大提高了系统的效率。
3)DMC由预测模型、滚动优化和误差反馈矫正3个部分组成,只要提前获得系统的阶跃响应曲线就可以进行控制,与系统的模型和参数无关,有较强的可移植性和兼容性。
本文通过优化系统的电流应力和回流功率,减小系统的导通损耗,并未考虑开关管是否工作在软开关条件下。后续工作将进一步考虑开关管的软开关条件,使开关管实现零电压开通,减小开关损耗,以提高系统效率。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

