基于改进NSGA-Ⅱ 算法的某连续刚构桥纵向钢束设计优化研究

梁茜雪

(广西交科集团有限公司，广西 南宁 530007)

0 引言

连续刚构桥是众多桥梁体系中的一种，因其具有结构刚度大、伸缩缝较少、行车安全舒适以及养护简单等特点得以广泛应用。目前，我国大规模地建设和发展大跨度连续刚构桥梁，但连续刚构桥纵向预应力筋的布置、设计优化是目前面临的一个难题，其涉及多因素相互作用、相互影响的问题。目前学者对于预应力钢束优化已有所研究：董学申[1]依托马过河特大桥提出了适应底板预应力束部分水平布置的最优方案，并对底板预应力束全部和部分水平布置两种方案下，在长期挠度、内力和应力方面的影响规律进行研究；陈久长[2]针对徐变系数、环境湿度等因素，分析了相关参数对于中跨下挠的影响规律，同时结合预应力度、体内外混合配束法对笋子岩大桥预应力束进行优化；许海哲[3]基于lingo软件，以各单元弯曲能量之和最小为目标函数，以合理截面应力为约束条件，得出优化后的预应力钢束用量及布置形式；孙磊[4]根依据传统预应力钢束设计计算方法，对于相关预应力布束进行优化，指出基于平面杆系设计需结合局部实体模型分析，分段锚固纵向短束代替集中锚固的纵向长束，可避免长束预应力损失严重的问题；方志[5]基于最小弯曲能量法，以离散截面的弯曲能量之和最小为目标函数，优化后得到了各阶段张拉的预应力钢筋数量。

本文依托某连续刚构桥工程研究背景，基于改进的NSGA-Ⅱ算法，结合Midas Civil有限元模型计算结果，对于六种不同类型钢束进行优化，以钢束用量最少、截面平均正应力最小为目标函数，以各类型钢束用量比值以及桥梁使用阶段承载能力为约束条件，确定合理的钢束用量，提高效率，减小施工成本，为同类工程设计及施工提供借鉴和参考。

1 工程概况

本文依托某跨径布置为(45+85+45)m的连续预应力刚构桥为研究背景。该桥的各主墩“T”构纵桥向划分为11个对称梁段，边跨主梁现浇段长4.82 m，11号梁段采用挂篮悬臂浇注施工。全桥共有3个合龙段，合龙段长度为2 m(采用型钢桁架作合龙段劲性骨架)。箱梁顶宽16.5 m，底宽8.5 m，悬臂长度为4.0 m。箱梁根部断面梁高为8.0 m，现浇段和合龙段梁高均为3.2 m，其余梁底下缘按1.8次抛物线变化。箱梁根部底板厚60 cm，合龙段及现浇段底板厚32 cm，根部至合龙段按1.5次抛物线由60 cm渐变至32 cm。此桥为三向预应力体系，纵向与横向采用预应力钢束，竖向采用精轧螺纹粗钢筋。全桥立面布置如图1所示，箱梁截面如图2所示。

图1 桥梁立面布置图(cm)

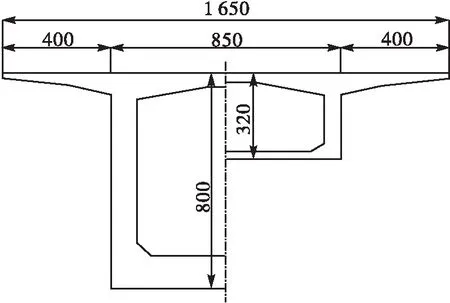
图2 箱梁截面布置图(cm)

2 改进的NSGA- Ⅱ 多目标优化算法

2.1 NSGA-Ⅱ 多目标优化计算原理

NSGA-Ⅱ 算法是由Deb等人提出的多目标优化算法，通过精英保留策略、拥挤度计算和快速非支配排序策略改进了NSGA算法的不足，降低了参数选取的难度，解决了原算法运行效率低的问题。其计算过程如下：

(1)随机产生规模为Np的种群，即种群初始化。

(2)对于种群进行快速非支配排序，对于种群中每个个体进行Pareto等级的比较，从而得到其被支配数np，第一非支配层的个体np=0，完成整个种群的分级。

(3)依据目标函数fm值大小，将同非支配层的个体进行排序，而边界解之间的拥挤度nd无穷大，其余的个体拥挤度为：

(1)

(4)通过二进制竞标赛选择，任意比较两个个体Pareto等级高低，等级高的择优，若相同则选择拥挤度较大的个体，进入下一代种群。

(5)进行模拟二进制交叉和多项式变异，得到新的子代种群Ct，通过精英保留策略，保留父代种群Pt，将新种群与父代种群混合，再对这个混合种群进行非支配排序，将非支配集中的个体按Pareto等级高低依次放入新的父代种群Pt+1，当Pt+1数量超过Np，以拥挤度作为评判标准，剔除较小个体，使种群数量等于Np。

(6)重复进行步骤(4)、步骤(5)，直到满足设定的种群代数，即可获得Pareto最优解集。

2.2 NSGA-Ⅱ 多目标优化算法的改进[6]

非支配排序遗传算法 Ⅱ (NSGA-Ⅱ )所采用的快速非支配排序、拥挤距离排序以及精英保留策略，优化了结果精度，扩大了全局搜索范围，保证了种群多样性，可以很快寻找到全局最优解。

本文针对上述步骤(5)中二进制交叉和多项式变异进行相应改进，引入NDX(正态分布交叉算子)代替原算法中的SBX(二进制交叉算子)，进一步扩大搜索空间，保证种群多样性。在交叉运算中，基于选中的父代p1、p2，通过NDX得到子代x1、x2，对于第i个变量，利用如下过程进行交叉运算，其中|N(0,1)|为正态分布随机变量：

(1)随机数t产生，t∈(0,1]。

(2)若t≤0.5，则：

(2)

(3)若t>0.5，则：

(3)

对于原算法中的多项式变异，考虑使用改进的自适应调整变异方式，提升收敛速度，提高了种群的多样性和稳定性。其变异算子将个体变异概率和适用度定义为：

(4)

式中:e(Xi)——个体Xi的适应度；

E(Xi)——Xi适应度评价函数；

Pm——其变异概率；

M——个体数量。

2.3 连续刚构桥预应力钢束优化模型构建

一般来说，刚构桥预应力钢束类型主要有顶板束、腹板下弯束、边跨底板束、中跨底板束、边跨合龙束以及中跨合龙束六种类型。本文根据遗传理论原理，对于六种优化前后钢束用量比值的约束变量采用浮点数进行编码，对于染色体向量X，若含有n个变量，其编码形式为：X=(x1,x2,…,xn),xi∈R,i=1,2,…，n。

2.3.1 目标函数构建

连续刚构桥钢束优化主要通过改变其布置形式以及钢束的数量，在满足承载能力前提下，尽可能使得全桥受力均匀合理，钢束用量最少。基于以上分析，确定以截面平均正应力最小、钢束用量最少[7]为优化目标结果。

(5)

以全桥钢束总量为优化目标函数，假定m(i)表示为第i钟类型钢束用量，则目标函数如式(6)表示：

(6)

2.3.2 约束条件构建

在进行钢束优化设计时，一般先确定初始钢束布置方案，本文采用优化后钢束面积与初始设计面积比值来表示。依据设计以及施工监控经验，约束条件表示为：

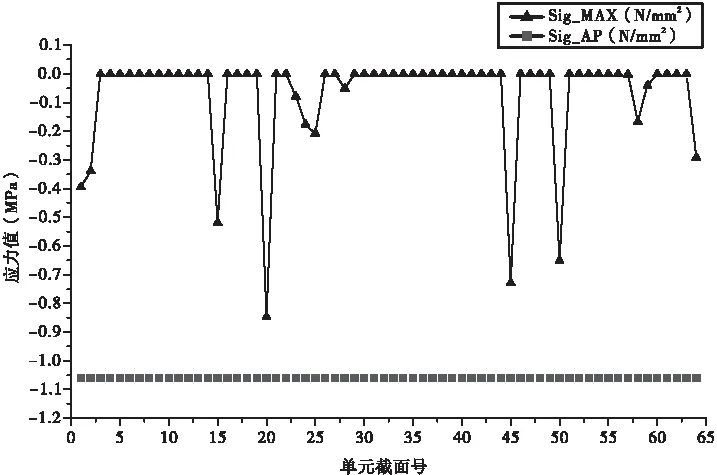
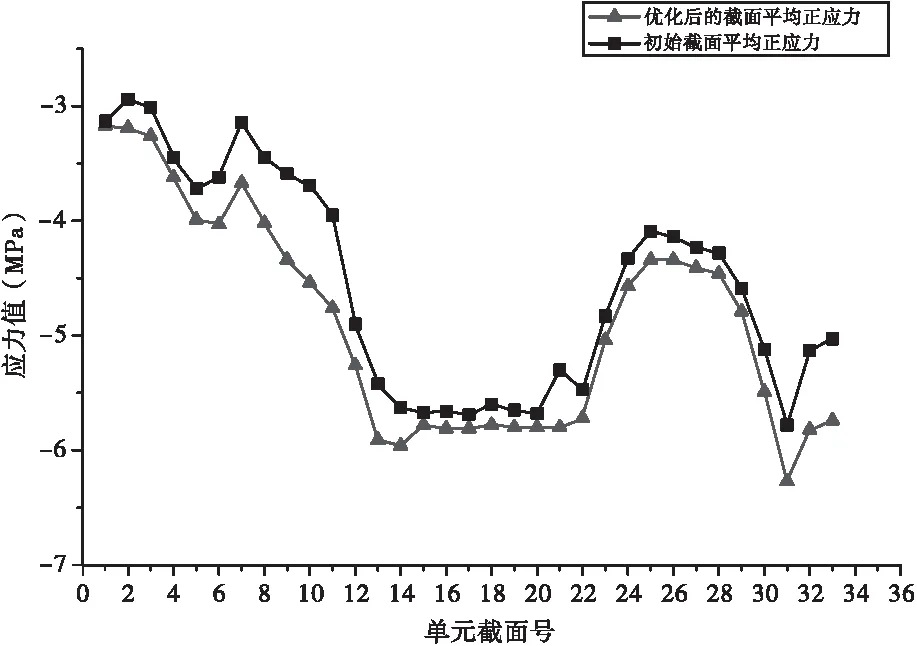
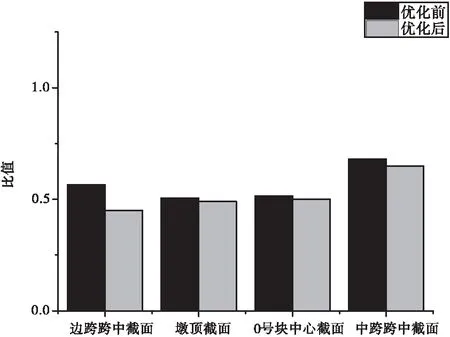
0

(7)

满足上述约束条件的同时，还需要桥梁承载能力满足要求[8]，即：

使用阶段正截面混凝土抗裂验算：σst≤0.8σpc；

使用阶段斜截面混凝土抗裂验算：σtp≤0.4ftk；

使用阶段正截面混凝土抗弯验算：|M效|

2.3.3 预应力钢束优化流程

改进的NSGA-Ⅱ 算法基于原算法基本原理，建立各变量之间的关系模型，将上述NDX与自适应调整变异算子运用于其中，提高种群多样性以及择优进程速度，新种群适应度也得到提升。结合改进的NSGA-Ⅱ 算法基本流程，连续刚构桥预应力钢束优化算法流程如图3所示。

图3 优化算法流程图

3 有限元模型的建立

本文基于某主跨为85m的刚构桥工程项目，运用MidasCivil有限元软件建立全桥模型，整体结构共离散成127个节点、118个单元，墩底采用固结约束，支座处放开DX自由度，约束DY、DZ，二期恒载为100.7kN/m，布置双向两车道荷载，根据规范要求进行荷载组合，验算其成桥使用阶段承载能力。其有限元模型如图4所示。

图4 桥梁有限元模型图

4 预应力钢束优化结果分析

依据前述改进的NSGA-Ⅱ 算法原理，编制相应的计算程序，结合MidasCivil有限元模型计算相应的目标函数值以及进行承载力验算，单元截面号根据原设计施工图纸中的悬浇节段号来拟定，边跨划分为13个截面，中跨划分为24个截面，钢束形状及位置按照原设计布置，主要针对各类型钢束用量作为设计变量，承载能力验算工况按照规范进行组合。

4.1 预应力钢束优化结果

经过改进的NSGA-Ⅱ 算法优化，得到优化过后的钢束用量数据，同时根据优化后的数据结果，建立MidasCivil全桥模型。结果显示，成桥状态下，最大挠度为22mm，小于规定值141mm，结构刚度满足要求。其承载能力验算结果显示，均满足规范要求。具体各类型钢束用量如表1所示 ，验算结果如图5 ～7 所示。

表1 不同类型钢束用量表

图5 使用阶段正截面抗裂验算结果曲线图

图6 使用阶段斜截面抗裂验算结果曲线图

图7 使用阶段斜截面抗弯验算结果曲线图

4.2 预应力钢束优化前后结果对比研究

根据优化后的计算结果，相比于初始设计预应力钢束总用量的106.01t，优化后钢束总重为94.21t，下降了11.1%，减少了项目成本。对比优化前后截面平均应力曲线图(图8)，可以看出两条曲线走势基本一致，说明优化结果的合理性，同时证明了以平均应力作为优化的目标函数也满足要求。曲线在墩顶位置数值较为接近，在靠近中跨跨中位置相差较大，相比于墩顶应力情况，钢束优化对于中跨跨中影响更为显著。根据截面上、下缘应力比值柱状图(图9)，可以看出，优化前后对于截面上、下缘应力比影响不明显。总体来看，上缘应力与下缘应力比值都<1，说明截面下缘压应力具有更大的富裕值，可以有效地提高桥梁跨越能力。

图8 优化前后截面平均应力曲线图

图9 优化前后关键截面上、下缘应力比值柱状图

5 结语

本文以钢束用量最小、截面平均应力最小作为优化目标，将改进的NSGA-Ⅱ 算法应用到连续刚构桥纵向预应力钢束的优化设计中，在满足连续刚构桥的结构安全性、稳定性的情况下，可通过减少钢束数量来提高连续刚构桥纵向预应力钢束的施工效率，进一步降低成本，提高经济效益。上述研究结论总结如下：

(1)本文提出改进的NSGA-Ⅱ 算法结合有限元模型计算，在连续刚构桥纵向预应力钢束设计优化上，相比于传统设计，提高了工作效率，减少了时间和经济成本。

(2)设计优化后的连续刚构桥预应力钢束总量减少了11.1%，优化后的桥梁结构承载能力满足规范要求。优化前后，桥梁截面平均应力变化趋势基本一致，下缘有较大的压应力储备，跨径可进一步增大。

(3)本文的研究为连续刚构桥纵向预应力钢束设计提供了一种新思路、新方法，具有一定的参考价值和工程应用价值。