水体颗粒后向散射系数测量一致性对比实验研究
张 翾,何贤强*,龚 芳,朱乾坤
(1.南方海洋科学与工程广东省实验室(湛江),广东 湛江 524006;2.卫星海洋环境动力学国家重点实验室,浙江 杭州 310012;3.自然资源部 第二海洋研究所,浙江 杭州 310012)
0 引言
太阳光照射在海面上,一部分直接被海面反射回大气,另一部分则透过海-气界面进入水体内部。透过海-气界面的那部分透射光在下行的过程中,一部分被水体吸收,另一部分则被水分子和水中颗粒散射。部分上行散射光透过海-气界面,成为携带水体物质信息的离水辐射。离水辐射透过大气层后被水色卫星所接收,成为水色卫星遥感的信息源。
颗粒后向散射系数是水体固有光学量的基本参量之一,也是建立水色遥感分析和半分析模型的主要参数。现场准确测量水体颗粒后向散射数据,对于水色遥感模型构建和水色遥感产品真实性检验至关重要。根据定义,后向散射系数bb为后向半球内的散射积分,即:
(1)
式中:β为体散射函数,θ为散射角,λ为波长。理论上,要准确获得后向散射系数,需要测量后向半球的所有角度散射光。但实际上,要测量全部角度不仅耗时,且对仪器研制也是很大的挑战,因为即使在后向半球,体散射函数值也有达几个量级的变化[1]。因此,为了实现快速测量,国际上研发了多种后向散射系数测量仪,如VSF3,BB9和HydroScat6等。这些仪器均不是逐个角度测量体散射函数,而是测量某个特定角度或几个角度的体散射函数值,然后近似估算后向散射系数。估算方法总体上可分为两种,一种是运用积分中值定理,将体散射函数和后向散射系数的积分关系转换为乘积关系,如BB9和HydroScat6采用这种方式;另一种是从后向散射系数的定义出发,测量若干个固定角度的体散射函数值,通过拟合获得函数,然后进行积分得到后向散射系数,如VSF3。这两种方法都使用了近似方法来估算后向散射系数,因此,测量结果会存在一定的差异。目前,对不同后向散射系数测量仪的结果差异的研究较少。BOSS et al[2]在长时间序列站进行的现场实验结果显示,VSF3和HydroScat6拥有较好的一致性。TWARDOWSKI et al[3]对比了HydroScat6和BB3的测量结果,发现它们之间有10%的偏差。这些研究比较的是颗粒后向散射率(后向散射系数与总散射系数的比值),而并非直接的后向散射系数。
本文针对当前对不同的水体颗粒后向散射系数原位测量仪结果差异缺乏认识的问题,通过实验室比测实验,对3种原位测量仪(HydroScat6,VSF3和BB9)的结果一致性进行分析,并通过T矩阵法模型模拟研究不同颗粒形状对后向散射系数测量结果的影响。
1 实验方法
1.1 原位测量仪简介
HydroScat6测量的是6个波段(420,442,470,510,590和700 nm)的140°体散射函数;BB9测量了9个波段(412,440,488,510,532,595,650, 676和715 nm)的117°体散射函数;而VSF3所测为3个波段(470,532和650 nm)、3个角度(100°,125°和150°)的体散射函数。
HydroScat6和BB9均通过式(2)将体散射函数转换为后向散射系数:
bb=2πχβ(θ)
(2)
式中:χ为转换系数。HydroScat6和BB9所不同的是转换系数选取,HydroScat6取1.08[4],而BB9则为1.1[5]。
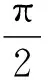
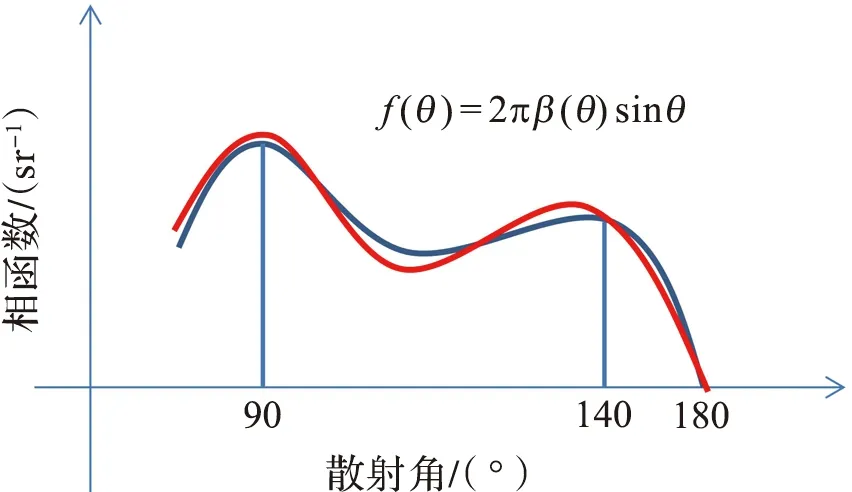
图1 后向体散射函数示意图Fig.1 Sketch map of backward volumescattering function
1.2 实验材料
室内实验所采用的颗粒有两种,一种是人工合成的标准球形颗粒,另一种是野外采样所得的泥沙颗粒。标准球形颗粒是由矽比科公司生产的型号为SS250的球形石英颗粒,其粒径分布如图2所示。野外采样颗粒来自钱塘江北岸,具体位置见图3。野外采样颗粒取自丁字坝处潮水退去后的淤积泥沙,使用干净的勺子舀进广口瓶中带回实验室。在实验室中将泥沙样品放入烘箱中干燥,去除水分。干燥后按实验时质量浓度增加所需要的泥沙量进行称重,并放入保存盒内备用。另外,为了检验颗粒形状是否会对体散射函数和后向散射系数产生影响,利用T矩阵模型模拟计算了不同颗粒形状下的体散射函数和后向散射系数。

图2 标准球形颗粒粒径分布Fig.2 The distribution of standard spherical particle’s size
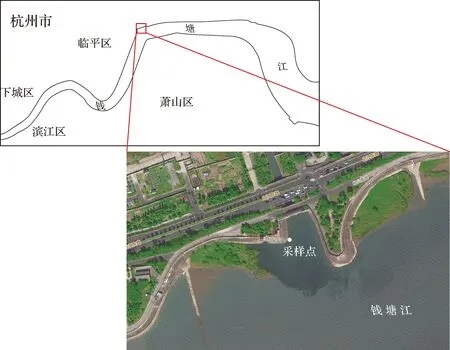
图3 野外采样点位置示意图Fig.3 Location of sampling station
1.3 实验步骤
3种水体颗粒后向散射系数测量仪(HydroScat6,VSF3和BB9)的实验室比测过程如下:(1)在内壁全黑的塑料桶中注入固定体积的去离子水,静置24 h以去除气泡;(2)实验开始前先对桶内去离子水进行测量,以此作为本底值,并与纯水理论值进行比较以检验桶壁和底部反射对测量结果的影响;(3)实验开始后,依次加入事先称重过的颗粒样品(分别包括人造球形颗粒和天然野外水体颗粒),并混合均匀,之后3台仪器交替测量。为了防止颗粒的沉淀,在仪器交替测量之间再次将水体混匀。为了保证实验的可重复性,同一质量浓度下每台仪器均测量3次,3台仪器交替进行。
为了使实验水体能够模拟清洁的大洋一类水体和近岸浑浊的二类水体,实验水体的颗粒质量浓度值设定为0~100 mg/L。但是由于颗粒沉降及水体体积误差等因素,实际颗粒质量浓度和预设值有较小的偏差,具体数值见表1。

表1 实验中实际水体颗粒质量浓度Tab.1 Actual concentration of particles in the experiment
2 结果和讨论(1) 数据处理均依照仪器用户手册进行。
2.1 纯水测量结果
图4是实验之前由HydroScat6所测的纯水后向散射系数结果,其中蓝线为Morel纯水模型的计算结果[6]。可以看出,测量结果和理论模型计算结果非常接近,说明实验背景水体中颗粒含量很少,且桶的内壁和底部对实验结果影响较小。
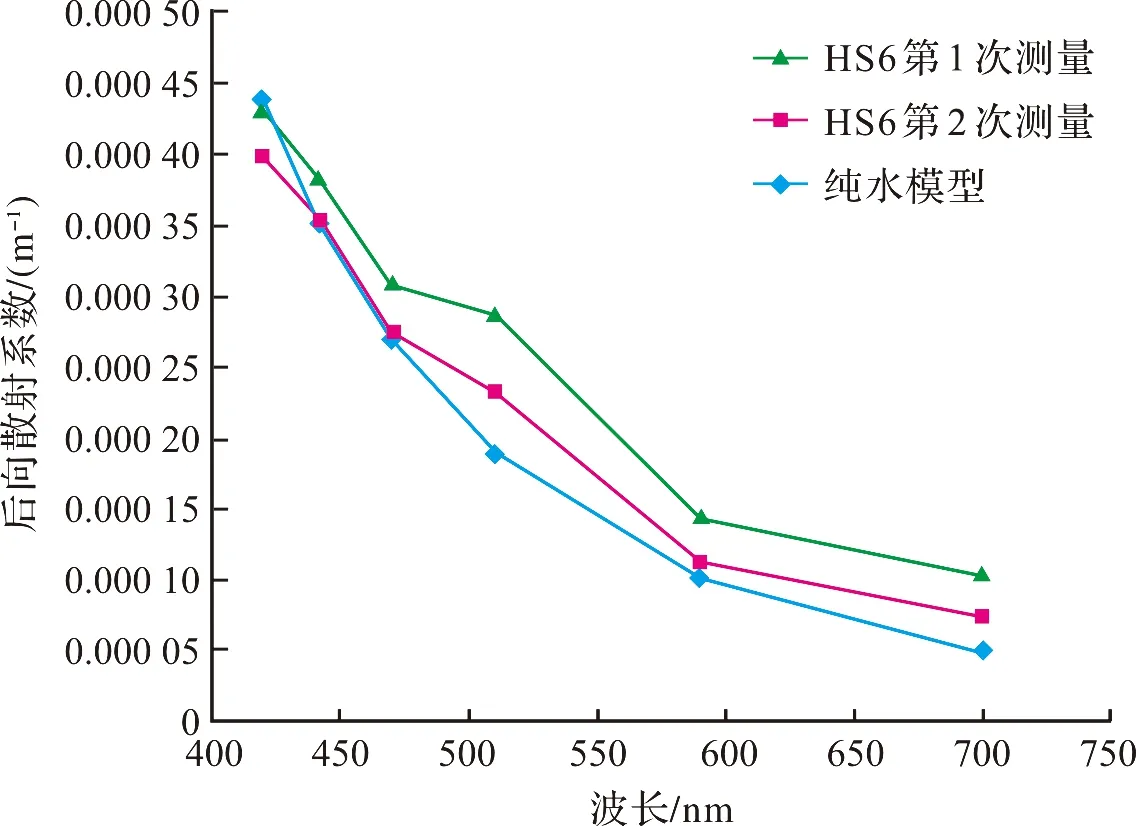
图4 纯水140°体散射函数HydroScat6两次测量结果与理论值的比较Fig.4 Comparison between HydroScat6 measuredresults and theoretical results in pure water at 140°
2.2 不同颗粒质量浓度的测量结果比对
图5是0.5 mg/L(代表大洋清洁水体)和50 mg/L 质量浓度(代表近岸浑浊水体)下的VSF3和HydroScat6测量结果比较,3次测量结果相差不大,可见实验具有较好的重复性。
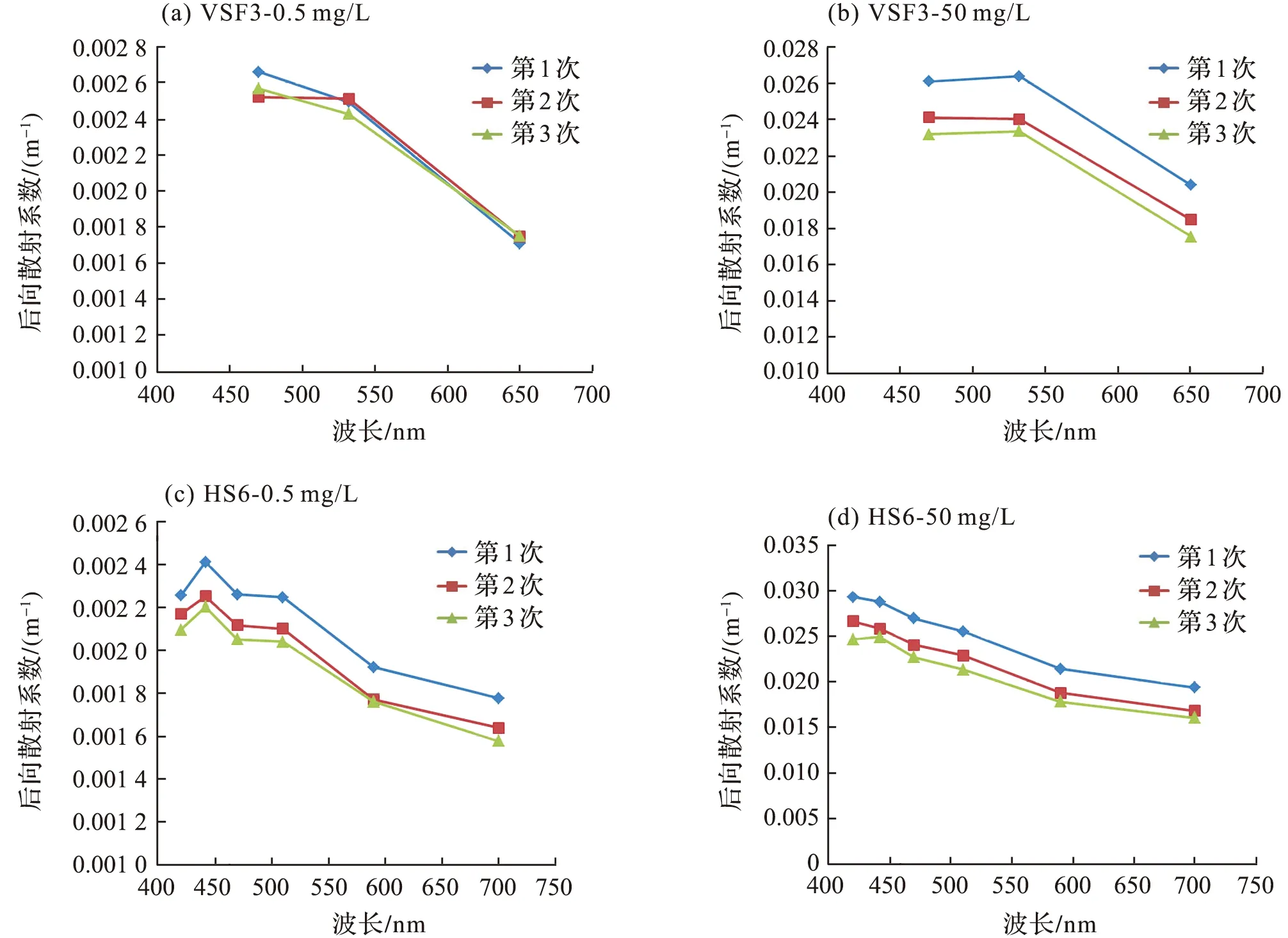
图5 不同颗粒质量浓度VSF3和HydroScat6测量结果比较Fig.5 Comparison of measurement results of VSF3 and Hydrocata6 at different particle concentrations
将3种仪器在不同质量浓度下的标准球形颗粒后向散射系数测量结果进行相互间比较(图6)。由于BB9没有470 nm波段,因此在比较时选用最接近的488 nm波段数据代替。总体而言,3台仪器有着较好的一致性,数据点基本处于1∶1线附近。其中HydroScat6和BB9的一致性最好,VSF3的结果在低颗粒质量浓度下和其他两者的结果一致,但在高颗粒质量浓度下(后向散射系数值大于0.06 m-1),VSF3的结果会偏小,可能是由于将体散射函数转化为后向散射系数的方法不同造成。

图6 3种仪器测量标准球形颗粒后向散射系数结果比较Fig.6 Comparison of backscattering coefficient of standard spherical particles measured by three instruments
图7为3种仪器在不同质量浓度野外采样颗粒下的后向散射系数测量结果比较。图8为将BB9在488 nm的测量数值线性插值到470 nm后与其余两台仪器的对比。和标准球形颗粒结果相比,野外颗粒测量结果的一致性较差,数据点相对较为偏离1∶1线。其中,HydroScat6和VSF3的结果较为一致,而BB9的结果大于前两者。在低质量浓度下,HydroScat6和BB9的结果较为一致,而在高质量浓度下则BB9的值会偏高。而VSF3在较低质量浓度时其值高于BB9,在高质量浓度时则低于BB9。
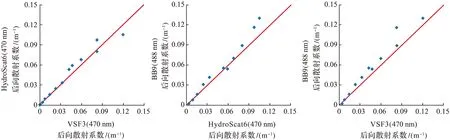
图7 3种仪器测量野外采样颗粒后向散射系数结果比较Fig.7 Comparison of backscattering coefficient of field sampling particles measured by three instruments
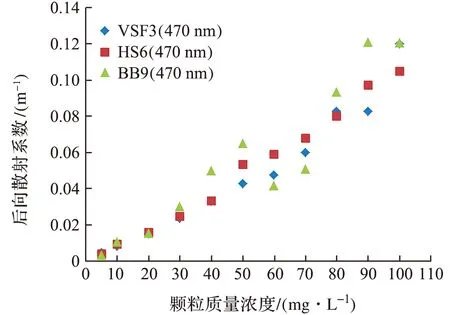
图8 野外采样颗粒测量结果比较Fig.8 Comparison of backscattering coefficientof field sampling particles(BB9的值线性插值成470 nm。)(BB9’s value linear interpolated to 470 nm.)
从以上室内实验比测结果可以发现,在低颗粒质量浓度水体中,3种仪器的测量结果一致性较好;而在高颗粒质量浓度水体中,三者的差异显著变大。同时,标准球形颗粒测量结果的一致性要优于野外采样颗粒测量结果,因此,不规则的野外颗粒形状可能对测量结果一致性产生影响。
2.3 颗粒形状影响模拟分析
采用T矩阵法模拟分析不同颗粒形状对后向散射系数的影响。T矩阵法是基于麦克斯韦方程快速计算非球形颗粒散射的有效方法,它由WATERMAN[7]首次提出。本研究所使用的T矩阵法代码由美国NASA的MISHCHENKO[8]开发,可用于计算3种形态的非球形颗粒散射,包括椭球体、圆柱体和切比雪夫颗粒。这3种颗粒均为回转体,通过改变颗粒的长短轴之比,可以改变颗粒的形状。以椭球体颗粒为例,当长短轴之比为1时,颗粒即为球体;当长短轴之比大于1时,则在回转轴方向上颗粒为扁椭球体;当长短轴之比小于1时,在回转轴方向上颗粒为长椭球体。
为了验证模型的正确性,首先将其与经典的Mie散射模型计算结果进行比对。Mie散射模型是针对球形颗粒,因此为了将两者的计算结果进行对比,将T矩阵模型的模拟颗粒也设为球形颗粒,即球体的长短轴之比设为1。同时,为了使模拟结果具有可比性,两个模型的输入参量设为一致,入射光波长为470 nm,颗粒折射率实部为1.165,虚部为0,角度分辨率为2°。比对结果如图9所示,可以看出,两者结果很一致,说明T矩阵模型计算结果可信。
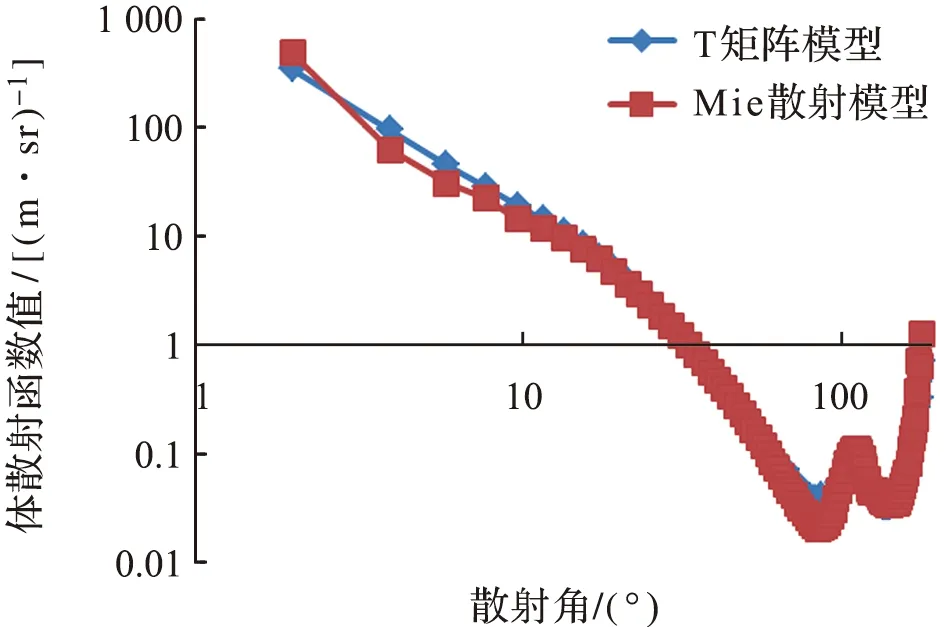
图9 T矩阵模型和Mie散射模型计算球形颗粒体散射函数值结果的比较Fig.9 Comparison results of T matrix model andMie scattering model for the volume scatteringfunction value of spherical particles
利用T矩阵模型进行不同颗粒形状的散射模拟。模拟颗粒假定为椭球体,粒径分布为对数正态分布,入射波长为470 nm,颗粒散射角度的采样间隔为2°。另外,假定颗粒材质为二氧化硅,其复折射率实部为1.165,虚部为0。通过改变颗粒的长短轴之比,即可计算得到不同椭球体的体散射函数。
图10为不同长短轴之比情况下的体散射函数结果,可以看到,颗粒形状对整个体散射函数随散射角变化趋势没有很大的改变。图11为其中后向半球部分的结果(注意未取对数坐标),可以发现后向半球部分的体散射函数受颗粒形状的影响较大。特别是当颗粒长短轴之比为0.7和0.8时影响最大。颗粒形状对体散射函数影响较大的峰值位于110°附近。当长短轴比在0.7和1之间变化时,体散射函数在后向半球范围内达到的第一个峰值的角度也在不断变化。当长短轴比从0.7开始增大,峰值位置会往大散射角偏移,在长短轴比为1时,峰值位置达到最大散射角,约为114°,而此时颗粒从扁球体变成球体。当长短轴比在1至1.5之间变化时,峰值位置又重新往小散射角偏移。当长短轴比为1.5时,峰值位置达到最小散射角,约为94°。
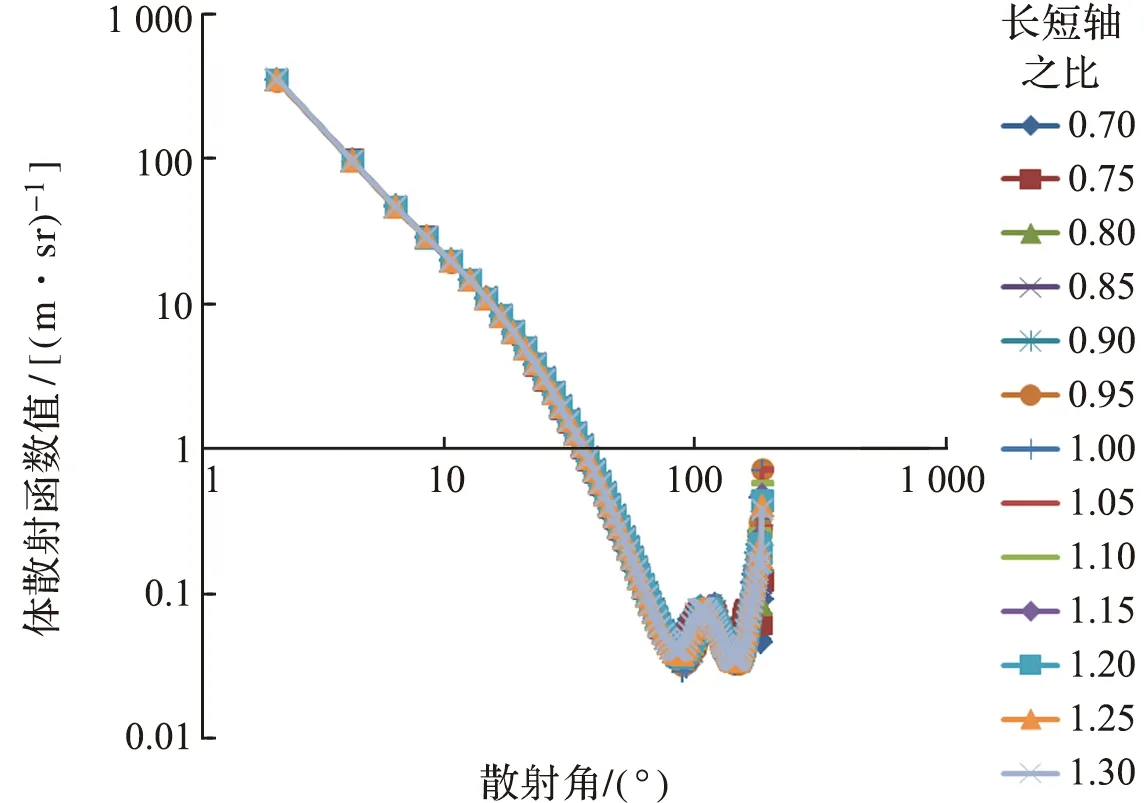
图10 不同长短轴比情况下体散射函数值随散射角的变化Fig.10 The change of volume scattering functionvalue with scattering angle under different ratioof long axis to short axis

图11 不同长短轴比情况下后向体散射函数值随散射角的变化Fig.11 The change of volume backscattering functionvalue with scattering angle under differentratio of long axis to short axis
从上述结果可以看到,不同颗粒形状对体散射函数的后向散射部分有一定的影响。因此,对通过测量某个或几个固定角度的后向体散射函数值来估算后向散射系数的现场仪器来说,不同颗粒形状将会产生多大的影响呢?我们将模型计算所得的不同长短轴之比下的体散射函数,取仪器测量角度(100°,117°,125°,150°和140°,其中117°和125°由插值得到)对应的体散射函数值,再按照仪器计算后向散射系数的方法估算后向散射系数值。以球形颗粒为基准,分析不同颗粒形状对3种仪器后向散射系数测量的影响百分比,结果如图12所示。可以看出,随着长短轴之比的变化,不同颗粒形状对后向散射系数产生影响。当长短轴差异越大,即长短轴之比离1越远,后向散射系数受到颗粒形状的影响就越大。比较而言,BB9所受影响最大;HydroScat6所受影响最小,除长短轴之比为0.7和0.75外,其余情况下影响均在10%以内;VSF3的影响处于两者之间。造成这一结果的原因,应该是由于不同颗粒形状对体散射函数影响所致。从图11可以看到,在不同颗粒长短轴之比下,140°的体散射函数值变化较小,而在90°至120°之间变化幅度较大。HydroScat6测量的角度是140°,BB9测量的角度是117°,所以BB9所受到的粒径变化影响相较HydroScat6要大。而VSF3所测的是3个角度的体散射函数值(100°,125°和150°),虽然受到不同角度的影响较大(尤其是100°),但由于其计算后向散射时采用的是插值拟合方法,将不同散射角造成的不确定性部分抵消,使得VSF3的结果反而要好于BB9。
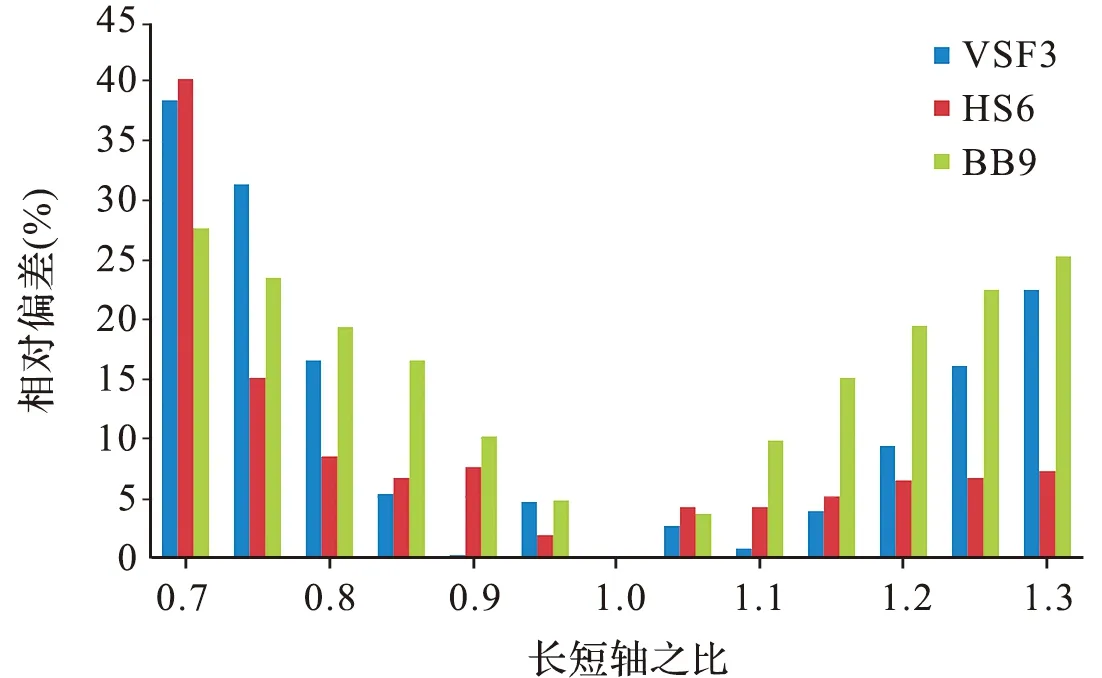
图12 颗粒形状对3种仪器后向散射系数测量结果的影响Fig.12 The influence of particle shape onthe measurement results of backscatteringcoefficient of three instruments
3 结论
颗粒后向散射系数是水体最重要的固有光学量之一,也是水色卫星遥感的关键参数。准确测量水体颗粒后向散射系数是水色遥感分析或半分析模型构建以及水色遥感产品真实性检验的重要前提。本文针对当前常用的2类不同观测原理的3种水体颗粒后向散射系数原位测量仪(HydroScat6,BB9和VSF3),通过比对测试实验,分析了三者测量结果的一致性。结果表明,3种仪器对清洁水体颗粒后向散射系数测量具有较好的一致性,但在浑浊水体中,HydroScat6和BB9测量值会比VSF3高,三者偏差显著增大。
同时,我们也发现,颗粒形状也会对测量结果产生影响,3种仪器对人造球形粒子测量结果的一致性要显著好于野外颗粒结果。通过T矩阵法模型,本文进一步分析了非球形颗粒对体散射函数的影响。结果表明,在散射角90°~120°之间体散射函数受颗粒形状影响较大,因此,相比于测量140°体散射函数的HydroScat6,测量117°体散射函数的BB9受颗粒形状影响更大;而测量3个角度体散射函数值,拟合估算后向散射系数的VSF3,则可能因为拟合过程将不同散射角造成的不确定性相互抵消,从而使它的结果位于以上两者之间。

