成网条件下地铁-公交复杂网络的末班车衔接优化
焦正玉,李引珍,苏 铭,陈晓明
(兰州交通大学交通运输学院,兰州 730070)
如今,城市轨道交通和常规公交已经成为居民日常出行的主要选择。城市轨道交通具有快速、准时、安全、运量大、节约资源和显著缓解地面交通压力等优点,在城市交通中起着中流砥柱的作用。目前,其建设进入了快速增长时期,有力地减轻了城市交通压力。自进入21世纪以来,全国公共交通的线路与车辆大幅增长,出行分担率不断增加,中国将公交优先作为城市发展的重大战略。城市交通是一个典型的复杂网络系统,通过城市轨道交通和常规公交的合理协同配合能够提高城市交通的系统性和可达性[1-3]。陈晓明等[4]通过节点重要度识别法添加新的轨道交通节点并建立地铁-公交双层复杂网络协同优化模型,提高地铁-公交换乘率。胡宝雨等[5]以局域网络内总协调次数最大化为第一目标,协同换乘子网络内多辆公交车与地铁产生协调的概率最大和最小为第二目标,建立双目标协调调度优化模型,并设计求解模型的启发式算法,得出与地铁协调的常规公交时刻表。梁金鹏[6]提出从地铁的需求和供给管理角度的管控策略出发,建立了不确定条件下的城市轨道交通客流控制和接驳公交网络设计优化模型,并设计了相关求解算法。孔雪等[7]从基础设施建设、服务质量和运行效益水平和与地铁的协同4个方面建立城市公交线网运行效率评价指标体系。
在城市轨道交通出行中,末班车阶段是一个出行日中极其重要的阶段。由于各线路结束运营的时刻不同,各车站之间的可达关系呈现动态变化的特点。一条线路的末班车时刻不仅影响本线乘客的出行,还通过到达换乘站的时刻从而影响整个路网。末班车的不合理衔接[8-10]也会导致乘客等待时间过长,运力资源浪费和换乘效率低下等问题,所以如何提高城市交通末班车的衔接状况是人们在日益增长的交通需求背景下最亟待解决的问题之一。徐瑞华等[11]通过分析城市轨道交通网络末班车衔接关系,考虑其复杂性和影响因素,在城市轨道交通各个线路之间的衔接关系基础上,建立了网络末班车衔接方案优化模型。宁丽巧等[12]在引入0-1变量和换乘失败惩罚系数的基础上,对末班车时段内列车衔接关系进行描述,构建末班车时刻表协同优化模型,表明该模型能有效生成大规模路网条件下城市轨道交通末班车时段列车协调衔接计划,提高了末班车时段各列车在换乘站的衔接匹配度。吴建军等[13]通过建立城市轨道交通网络末班车衔接的网络模型,采用衔接矩阵对网络特征量进行分析,从而确立对城市轨道交通末班车衔接能力可量化的评价方法,但未从复杂网络结构的方面说明复杂网络对于末班车衔接能力的优越性,也并未优化末班车的衔接能力。
针对城市轨道交通末班车换乘衔接能力低下的问题,现引入接运公交并结合双层复杂网络理论,建立地铁与公交网络的末班车换乘衔接模型。利用衔接矩阵将网络特征参量(度、最短路径、衔接比例)作为可量化的评价指标进行对比分析,说明地铁-公交双层复杂网络相较于城市轨道交通网络在末班车衔接效率、次数和成功率方面的显著优势,表明地铁-公交双层复杂网络的协同运输能够有效缓解末班车衔接不合理的问题。同时,延后换乘衔接失败率较高车站所在的线路的末班车时刻,以达到提高末班车衔接成功率的目的。
1 网络模型
1.1 城市轨道交通网络末班车换乘衔接模型
城市轨道交通网络是动态变化且复杂的系统,其网络形态结构呈现出不同的特性,可以综合运用交通运输工程、系统科学理论进行研究。以复杂网络理论[4]为基础,将车站抽象为节点,车站之间的区间抽象为边,以线路运营时刻表为基础,建立城市轨道交通末班车网络模型,数学模型表述为
G=(V,E)
(1)
式(1)中:G表示城市轨道交通末班车网络;V表示节点的集合,V={Vi},i=1,2,…,n,Vi表示第i个换乘站,n表示换乘站总数;E表示换乘站之间末班车的衔接关系,E={eij},i,j=1,2,…,n,eij表示第i个换乘站到第j个换乘站是否能衔接成功。
根据实际城市轨道交通每条线路末班车的运营时刻表得到各个换乘站的末班车运营时刻表,从而可以得到城市轨道交通网络各个线路末班车的衔接关系,采用分上下行的方法将不同线路末班车可以衔接的方向和同一条线路立折的情况通过城市轨道交通末班车网络有向图进行表示,如图1所示。其中,箭头表示城市轨道交通网络中不同线路末班车之间可以衔接的方向。
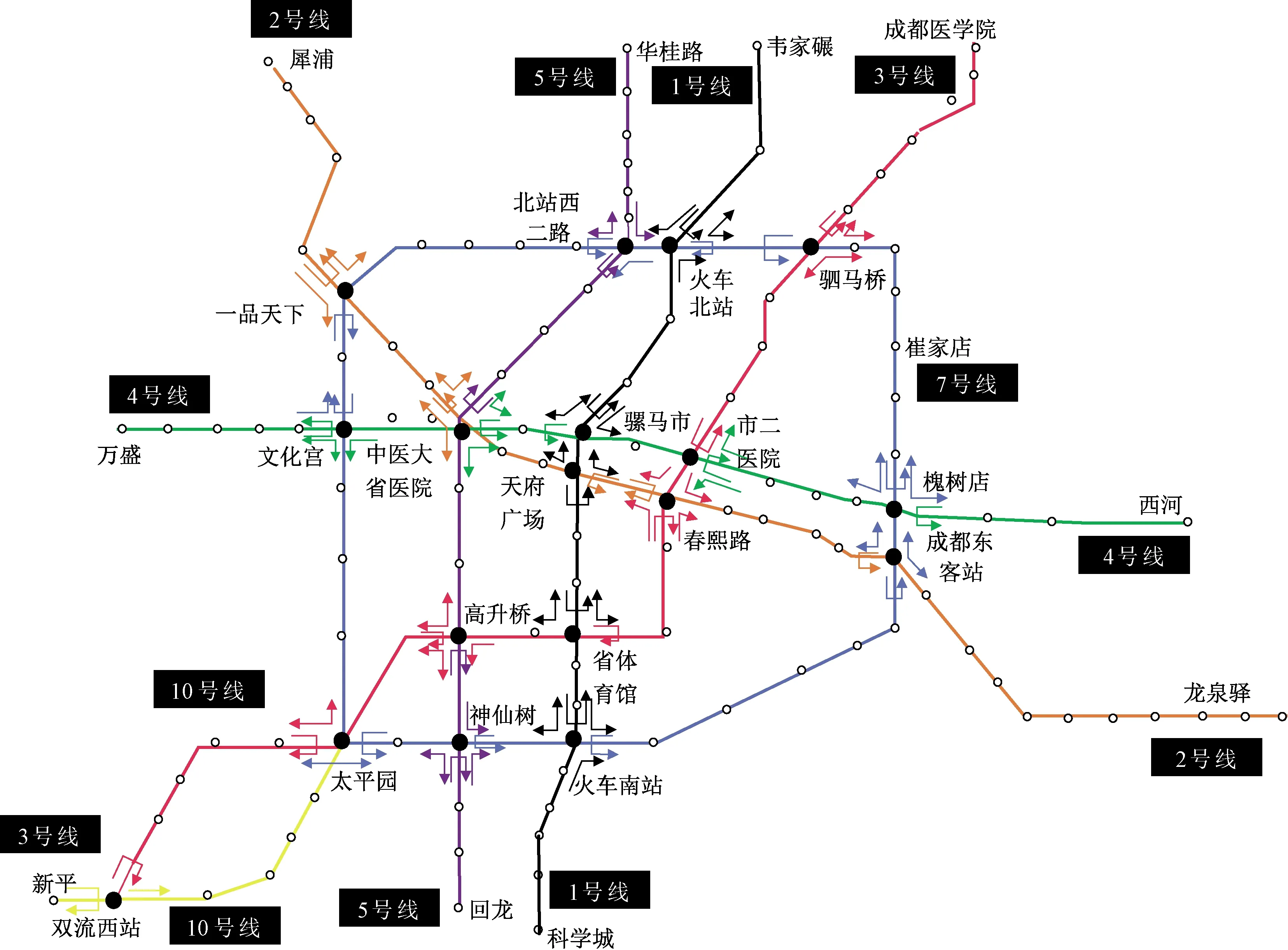
图1 成都市轨道交通网络及末班车衔接图
同时,将车站和区间分别用顶点、有向边进行映射。由于本文研究的是末班车乘客的换乘情况,因此仅考虑将线网中的换乘站作为网络的节点,例如2020年成都市城市轨道交通网络中有18个换乘站,那么对应的成都市轨道交通网络末班车衔接网络中便有同样18个节点。边由各个换乘站之间的衔接关系(可以直接到达、间接到达以及无法到达)进行表示。将两两换乘站点间可以直接到达的情况视为两两站点间存在有向边连接。确定好点以及点之间的连接情况后,便可以得到城市轨道交通网络末班车衔接有向拓扑结构图。以火车北站为例,得到部分城市轨道交通网络末班车衔接有向拓扑结构图,如图2所示。
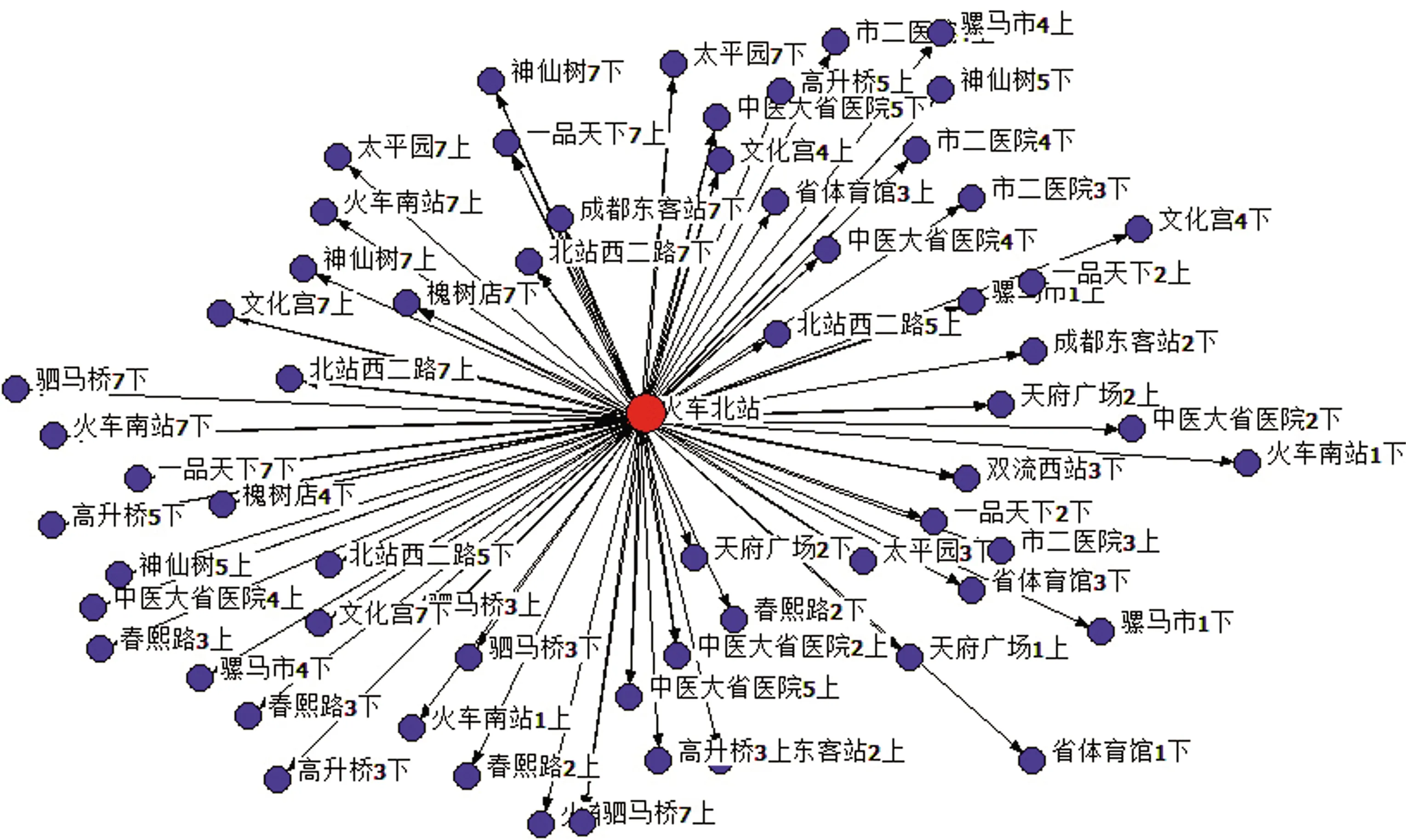
图2 部分城市轨道交通网络末班车衔接有向拓扑结构图
1.2 地铁-公交网络末班车换乘衔接模型
本文认为采用城市交通双层复杂网络能够协同优化多种交通方式的多层属性,因此在原有城市轨道交通网络的基础上引入成都市部分公交网络,如图3所示,来全面分析城市交通网络性能的优劣。

图3 成都市部分公交网络
同时,建立以实际线路运营时刻表为基础的地铁-公交双层复杂网络末班车的换乘衔接模型。本文引用陈晓明等[4]建立的双层复杂网络模型来表示城市轨道交通末班车网络和常规公交末班车网络。数学模型为
Gdou=GU+GL
(2)
Vdou=VU+VL
(3)
Wdou=WU+WL
(4)
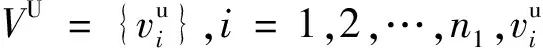
最后,利用该模型来描述车站与线路之间构成的拓扑结构,得到地铁-公交网络末班车衔接有向拓扑结构图。以火车北站为例,得到部分地铁-公交网络末班车衔接有向拓扑结构图,如图4所示,使得城市轨道交通与常规公交进行配合衔接,改善城市轨道交通末班车的衔接状况。

图4 部分地铁-公交网络末班车衔接有向拓扑结构图
2 复杂网络末班车换乘衔接矩阵和网络特征参量
2.1 复杂网络末班车换乘衔接矩阵
根据有向网络的定义,与一条边相关联的两个节点具有一定的次序关系,任一没有多重边和自连线的有向网络,可以用邻接矩阵来表示。基于本文所研究的是城市交通网络末班车的衔接关系,将邻接矩阵进一步赋予其物理意义如下。
(1)设城市轨道交通网络中共有n1个换乘站,其末班车换乘衔接矩阵用aij表示为
(5)
式(5)中:i,j=1,2,…,n1。
(2)设部分城市公交网络中共有n2个换乘站,其末班车换乘衔接矩阵用bst表示。
(6)
式(6)中:s,t=1,2,…,n2。
(3)设地铁-公交网络中共有n1+n2个换乘站,其末班车换乘衔接矩阵用cpq表示为
(7)
式(7)中:p=1,2,…,n1(n2);q=1,2,…,n2(n1)。
根据上述3种情况,结合以实际线路为基础的末班车时刻表,可以分别绘制出城市轨道交通网络末班车衔接矩阵和地铁-公交双层复杂网络末班车衔接矩阵,部分成都市轨道交通网络末班车衔接矩阵和部分成都市地铁-公交双层复杂网络末班车衔接矩阵如表1、表2所示。

表1 部分成都市轨道交通网络末班车衔接矩阵
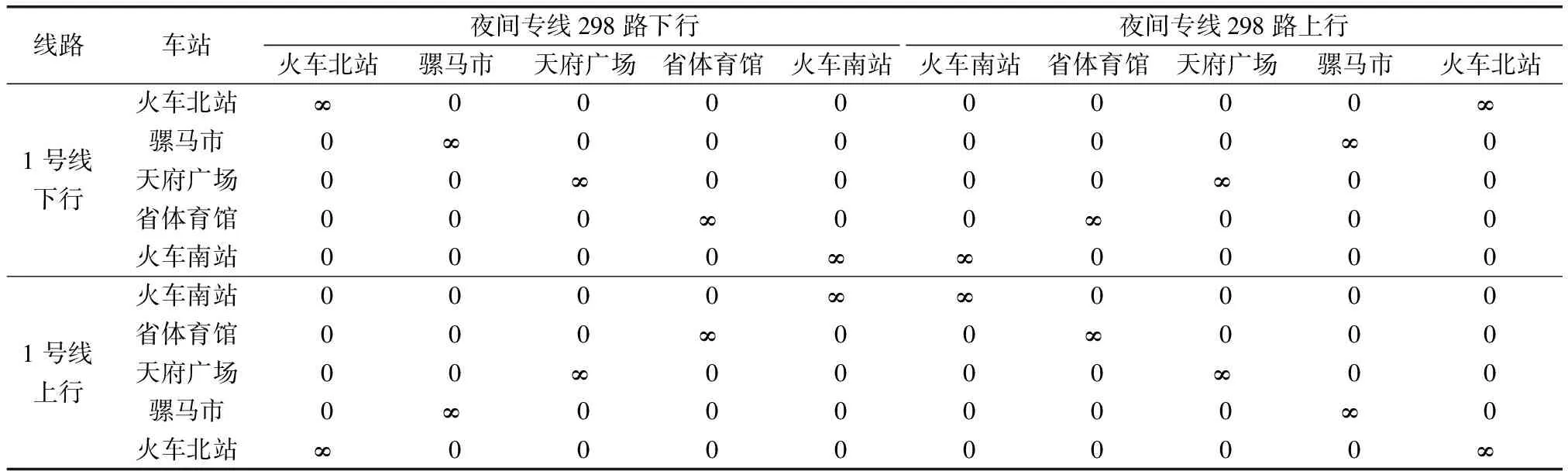
表2 部分成都市地铁-公交双层复杂网络末班车衔接矩阵
2.2 网络特征参量
2.2.1 度
节点的度是指与该节点连接的边的数目,对节点度的分析是复杂网络中衡量该节点与其他节点联系重要度的最简单的统计量。节点i0总的度为
(8)
2.2.2 最短路径
将节点i和j之间的距离dij定义为连接这两个节点的最短路径所包含的边的数目。两个节点i和j相连通是指在网络中节点i沿着某条边可以到达节点j。因此,dij=∞表示i和j不连通,而dij=0表示i和j连通(此时i和j表示同一节点)。网络平均路径长度L表示所有节点对N之间距离的平均值,即
(9)
2.2.3 衔接比例数
城市轨道交通网络末班车的衔接状况可以分为衔接成功和衔接失败两类。因此,将末班车能衔接成功的站点对设为N1,末班车不能成功衔接的站点对设为N2,衔接比例数即可表示为
(10)
为了简化统计N1、N2,对末班车路网换乘及发车时间作如下处理。
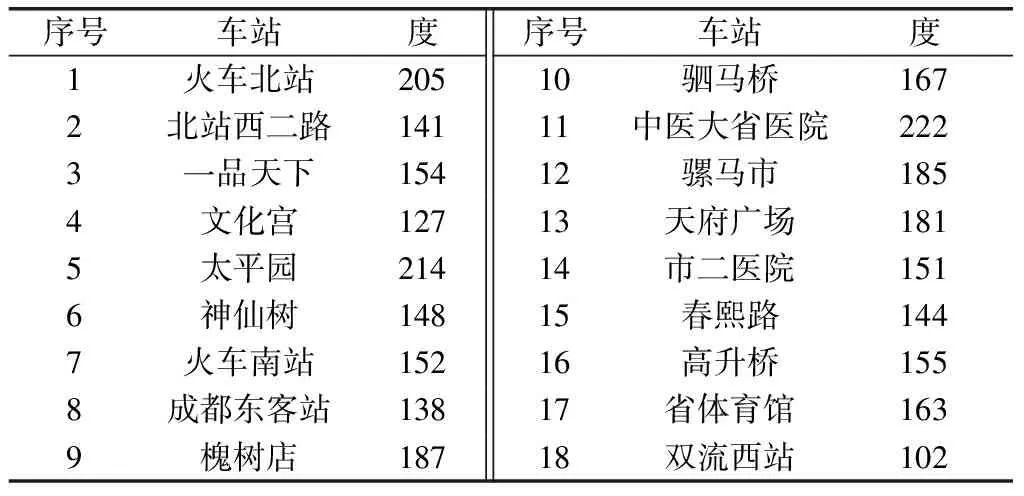
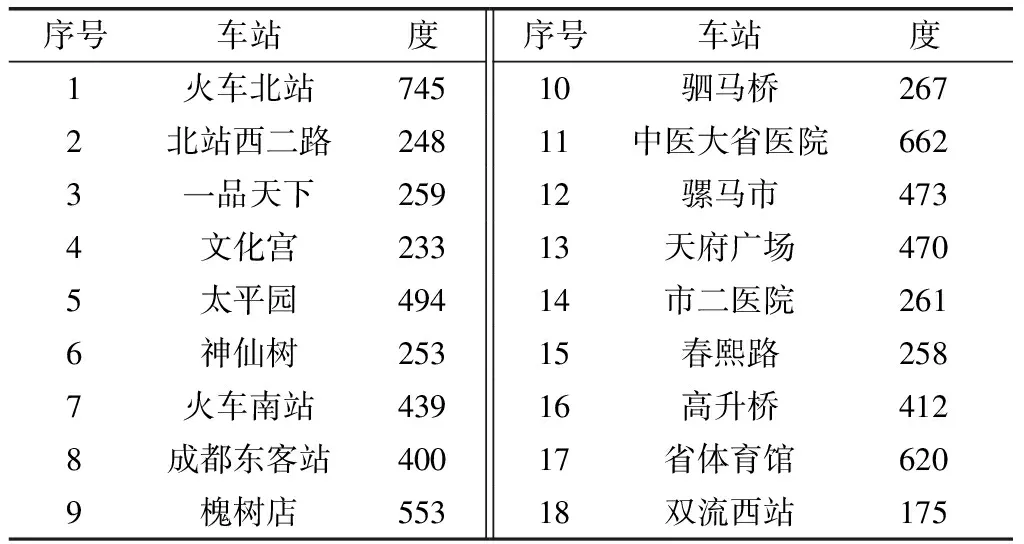
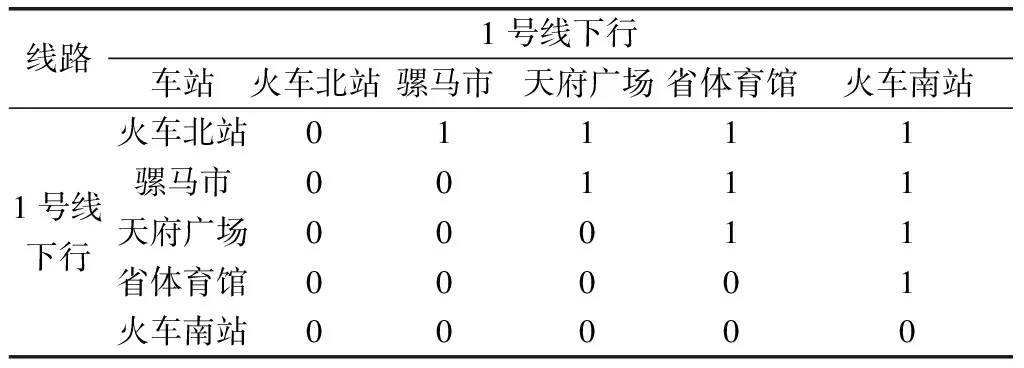
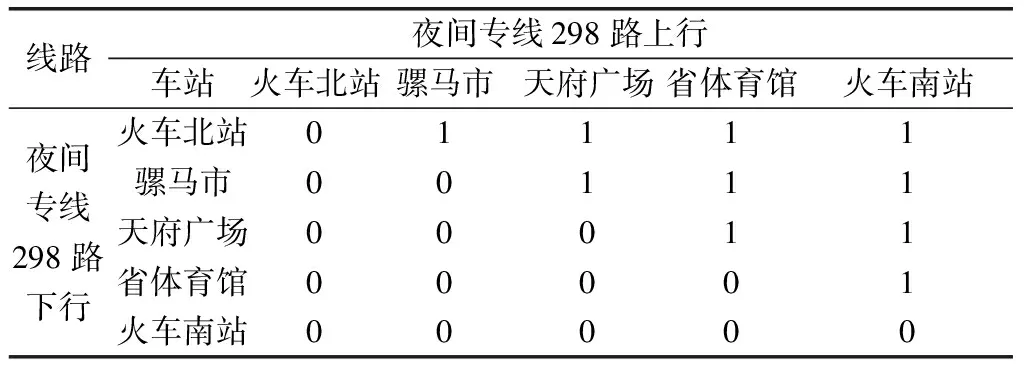
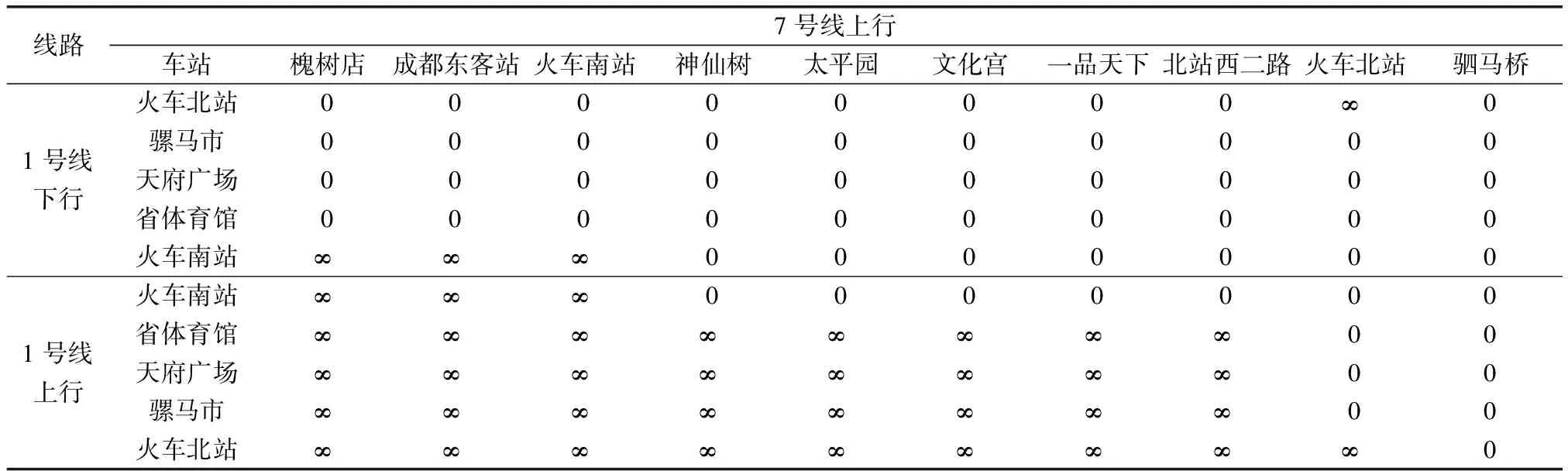
(1)当tio (2)当dso (3)当tio 其中,tio是第i条地铁到达o站的时刻;tjo是第j条地铁到达o站的时刻;dso是s路公交车到达o站的时刻;dto是t路公交车到达o站的时刻;δ1、δ2、δ3分别为地铁换乘地铁、公交换乘公交、地铁换乘公交的最小换乘时间,这里引用袁少华[14]在城市轨道交通和常规公交换乘模型问题研究中的方法,通过δ=δRBT+δRBF计算得到最小换乘时间,其中δRBT是换乘成功时的平均换乘时间,δRBF是换乘失败时的平均换乘时间。 对成都市轨道交通和常规公交进行实证分析。截至2020年6月,成都市地铁共有7条运营线路,线路总长302.285 km,共计207座车站,其中包含18座换乘站。同样,截止到2018年12月,成都公交拥有786条公交线路和13 939辆公交车。 由于公交站点过于繁多,考虑到本文的研究目的,构建的部分成都市公交网络中的公交站点选取与地铁站点同名,并忽略其具体位置的停靠差异[15]。 由于某换乘站度的值只与该换乘站所在线路上换乘站的数量及线路在该换乘站的末班车时刻表有关,从度的定义并结合具体换乘站网络末班车衔接矩阵,无法从根本上得到该换乘站在整个网络中的重要程度。因此,将直接衔接与间接衔接均计算为该换乘站的度。度反映该换乘站在末班车的衔接情况,体现出该换乘站的换乘效率。通过ucinet将成都市轨道交通末班车的衔接矩阵度和成都市地铁-公交双层复杂网络末班车衔接矩阵度计算出来,结果如表3、表4所示。 表3 成都市轨道交通网络换乘站末班车衔接矩阵度 表4 成都市地铁-公交双层复杂网络换乘站末班车衔接矩阵度 由于度比较大的节点在整个网络中起领导性的作用,度越大,该节点与其他节点所连接的边越多,换乘站越重要,换乘效率越高。从表3、表4可以看出,中医大省医院的度最大,表示其换乘效率最高;双流西站的度最小,表示其换乘效率最低。通过对比可知,当单层的城市轨道交通末班车网络升级为双层的地铁-公交末班车网络以后,其度较原来发生大幅增加,即换乘站末班车的换乘衔接效率发生显著性提高,表明将成都市地铁和公交末班车换乘网络衔接起来可以更好地满足末班车乘客出行换乘需求,提高末班车的换乘衔接效率。 目前,乘客通过“一票换乘”即可在不同线路的车站之间换乘出行,但由于各个线路末班车的运营时刻不同且各换乘站之间的可达关系也不同,因此将依据各换乘站之间的最少换乘次数选择路径,研究末班车网络的可达性。最短路径越小,说明末班车网络的衔接次数越少,可达性越高。成都市轨道交通网络部分换乘站末班车最短路径矩阵和成都市地铁-公交网络部分换乘站末班车最短路径矩阵如表5、表6所示。 表5、表6中两个换乘站之间末班车无法到达的情况用0表示,两个换乘站之间末班车可直接到达的情况用1表示,2代表两个换乘站之间末班车需换乘1次到达,以此类推。 表5 成都市轨道交通网络部分换乘站末班车最短路径矩阵 表6 成都市地铁-公交网络部分换乘站末班车最短路径矩阵 根据表5、表6数据,通过ucinet可以计算出成都市轨道交通末班车网络平均最短路径为1.258,成都市地铁-公交的末班车双层复杂网络平均最短路径为1.399。通过对比可以发现,成都市轨道交通末班车网络和成都市地铁-公交的末班车双层复杂网络的平均需要换乘的次数均不到1次,表明大部分末班车可以直接到达或者仅需换乘1次。同时,表明将单层的城市轨道交通末班车网络升级为双层的地铁-公交末班车网络,其最短路径仅增加了0.141,并不会明显导致换乘次数的增加,侧面也说明了成都市公共交通末班车可衔接站点间的衔接状况良好。 根据成都市轨道交通网络末班车换乘衔接矩阵,矩阵中1、0的个数即为末班车衔接成功的站点对数,即N1=1 468。因此,轨道交通网络末班车换乘衔接其所占的比例(衔接成功的比例)为N1/(N1+N2)=1 468/(1 468+4 308)=25.4%。同理,对于地铁-公交末班车换乘衔接矩阵,N1=4 394,地铁-公交末班车换乘衔接网络衔接成功的比例为:N1/(N1+N2)=4 394/(4 394+6 842)=39.1%。 由成都市城市轨道交通网络和地铁-公交网络末班车换乘衔接成功比例的对比可以看出,成都市地铁-公交的末班车双层复杂网络的衔接成功率较成都市城市轨道交通末班车网络有大幅提高,提高了13.7%。因此,可以认为加入公交网络后大大改善了城市轨道交通末班车的衔接状况,充分发挥了运力资源,提高了城市交通末班车的服务水平。 通过统计已知的地铁各换乘站的末班车换乘衔接失败率,如表7所示。采用延后换乘失败率较高车站所在线路的末班车时刻,以降低漏乘人数,提高末班车换乘衔接成功率。 由表7可知,一品天下、文化宫、神仙树3个换乘站的末班车换乘衔接失败率最大,且该3个换乘站均位于地铁7号线上。因此,考虑延后地铁7号线的末班车发车时间,由原来的23:05推迟至23:25,得到新的地铁-公交双层复杂网络末班车衔接矩阵,优化后部分成都市地铁-公交双层复杂网络末班车衔接矩阵如表8所示。通过计算可以得到地铁-公交末班车双层复杂网络的换乘衔接成功率由原来的39.1%提高至40.7%,达到车了优化末班车时刻表、降低乘客漏乘人数的目的。 表7 成都市轨道交通网络换乘站末班车衔接失败率 表8 优化后部分成都市地铁-公交双层复杂网络末班车衔接矩阵 综上可以得到末班车换乘衔接优化效果图,如图5所示。由图5可以看出加入公交末班车网络并延后换乘失败率较高车站所在线路的末班车时刻,均能显著提高末班车换乘衔接成功率,提高城市交通末班车的换乘效率和服务水平。 图5 末班车换乘衔接优化效果图 结合研究成果,对地铁和公交衔接提出以下政策保障措施来提高末班车衔接的效率。 (1)通过分析网络特征参数,可以认为优化公交末班车的到站时间,即着重优化部分公交车的停运时间,能够显著提高末班车的换乘衔接成功率。 (2)可以考虑为换乘失败率较高车站分配接运公交,以大幅提高末班车的换乘衔接成功率,以改善末班车的换乘衔接状况。 (3)考虑开辟优化地铁-公交接驳线,使地铁和公交融合发展,提高末班车的换乘效率。通过精细化计算地铁末班车到达的班次以及乘客从地铁站内步行到接驳公交站的时间,推出“无缝连接零等候”的概念。重点强化地铁站与周边3~5 km内人员密集区的接驳,并采取“回头看”策略,及时配套接驳支线,形成走街串巷、招手即停的模式,避免导致乘客末班车换乘衔接失败。 为了提高城市交通客运服务水平和质量,应尽可能提高各线路列车尤其是末班车在换乘站的合理衔接。在城市轨道交通末班车网络的基础上加入公交末班车网络,提出了地铁-公交的末班车双层复杂网络模型,建立了末班车衔接矩阵,分别对城市轨道交通末班车网络和地铁-公交的末班车双层复杂网络的节点度、最短路径、衔接比例进行分析与对比。最后对成都市城市交通网络进行实证研究,得到如下结论。 (1)加入公交末班车网络后,换乘站节点度的值大幅增加,即末班车的换乘衔接效率显著提高,表明将成都市地铁和公交末班车网络衔接起来可以更好地满足末班车乘客的出行换乘需求。 (2)加入公交末班车网络后,最短路径仅提高了0.141,末班车乘客的平均需要换乘的次数仍不到1次,表明大部分末班车可以直接到达或者仅需换乘1次,表明成都市交通系统末班车可衔接站点间的衔接状况良好。 (3)加入公交末班车网络后,末班车换乘衔接成功率提高了13.7%,表明地铁-公交的双层复杂网络的协同运输能够有效缓解城市交通系统中末班车衔接效率和成功率低的问题。针对通过评价指标得到的换乘失败率较高的车站,延后其末班车所在线路的发车时间以改善末班车的换乘衔接状况,使得末班车换乘衔接成功率提高了1.6%,提高了城市交通末班车的服务水平。 通过延后换乘失败率较高车站的末班车时刻,仅能小幅度提高路网末班车衔接成功率,具有较大的局限性。同时,仅强调了地铁-公交双层复杂网络在末班车衔接问题上的优越性,可以根据客流出行的规律和不确定性等,进一步在微观层面上考虑将动态客流、时刻表等结合起来优化城市交通末班车换乘衔接网络。3 案例分析
3.1 末班车网络度分析
3.2 末班车网络最短路径分析
3.3 末班车网络衔接比例分析
3.4 基于换乘失败率影响的末班时刻优化
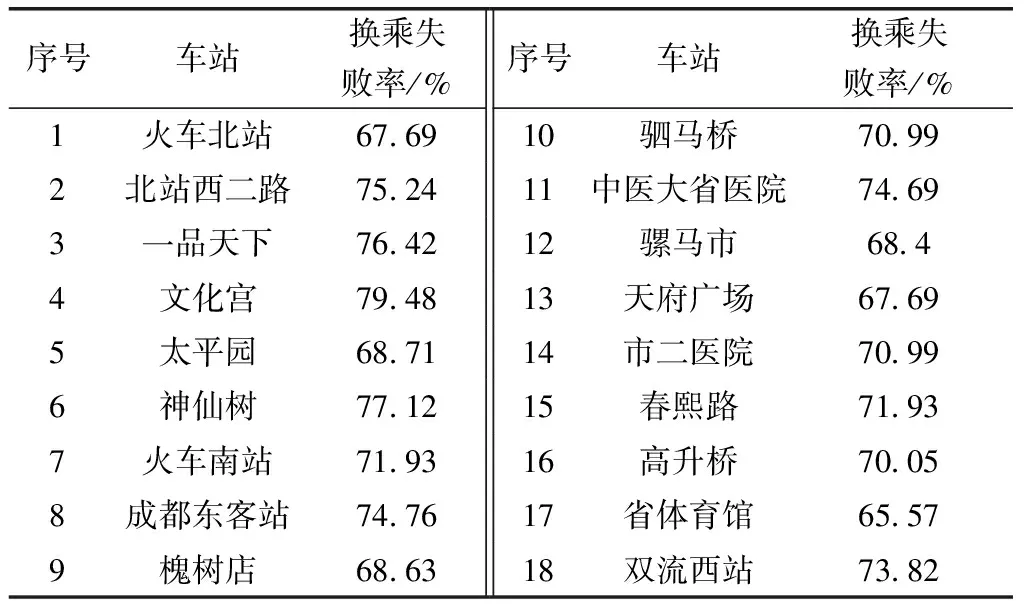
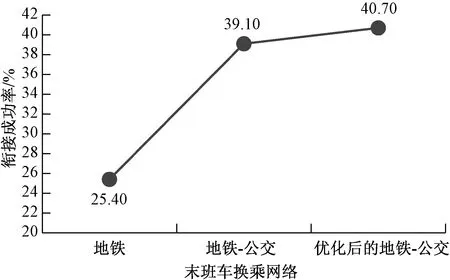
4 结论

