高地应力作用下隧道围岩三轴压缩破坏机制分析
刘 贺
(中铁十九局集团 第三工程有限公司, 辽宁 沈阳 110136)
0 引言
近年来,我国学者对处于高地应力环境中岩体的力学特性研究成果颇丰.田洪铭等[1-2]对高地应力环境中软岩隧道岩石进行了蠕变试验研究,基于岩石体积膨胀过程能量的耗散建立高地应力岩石损伤蠕变本构模型,同时田洪铭等还对围压在15~35 MPa条件下的泥质粉砂岩进行了应力松弛试验,结果表明,岩石的应力松弛主要包括衰减松弛阶段和稳定松弛阶段.邬爱清等[3]总结了近10年来深部岩石的试验方法、复杂应力路径下的力学特征、高地应力深部岩石的蠕变特征等相关问题,为今后进一步开展深部岩石力学工作指明了方向.陈景涛等[4]通过对拉西瓦花岗岩进行高围压下的真三轴试验,结合几种经典的岩石强度准则,建立了考虑高地应力作用的岩石强度准则.宫嘉辰等[5]基于波动方程,提出一种砂岩的纵波波速与高静水围压之间关系的数学模型,通过真三轴试验验证了其推导模型的合理性.李斌[6]以鄂州花岗岩为研究对象,对其进行了不同围压条件下的三轴压缩试验,并根据试验结果建立了考虑高围压条件的岩石强度准则.蒋海飞等[7-8]对砂岩进行了高围压高水压三轴压缩蠕变试验,并基于Burgers模型建立了考虑高围压高水压的砂岩蠕变模型.黄达[9]等通过对大理岩进行了不同卸荷速率及初始围压下的三轴卸荷试验,并结合分形理论和能量损伤理论,分析了高围压卸荷条件下岩石的损伤破坏机制和能量耗散机制.丁长栋等[10]通过高围压高渗透压致密砂岩三轴试验,对其在不同围压下的渗流情况进行了研究.杨以荣等[11]为研究石英云母片岩的能量演化特征,对其进行了三轴卸荷试验,从体积变形系数、能量比、能量变化率、能量应力增量比等方面对石英云母片岩的能量演化特征进行了分析.
综上,文章在总结前人研究成果的基础上,通过常规三轴压缩试验中设置高围压来模拟岩石所处的高地应力环境,分析高围压下砂岩的力学参数的变化特征,为工程实际提供可靠的理论依据.
1 试验介绍
1.1 试验设备
本文隧道砂岩高围压三轴压缩试验均在MTS815.03刚性伺服试验机上进行.该试验系统是由加压系统、测量系统以及控制系统组成,具备独立的轴压、围压、孔隙水压和动载4套独立闭环伺服控制功能.能够进行岩石类材料的单轴、三轴、渗透等多种岩石力学试验,且在加载过程中能够任意切换加载控制模式,以满足不同加载方式的需要.该系统的主要参数包括:压力框架刚度为11.0×106kN/m,轴向输出力范围0~4 600 kN,围压范围0~150 MPa,孔隙水压范围0~140 MPa.
1.2 试样制备及试验方法
本文试验砂岩取自辽宁某在建隧道项目现场,经XRD检测可知,试样的主要成分包括石英、长石、云母等.试样的干密度范围2.31~2.82 g/cm3,孔隙率范围0.58%~0.74%,颗粒粒径约为0.02~0.7 mm.为尽可能地保证试验误差在允许范围内,试样用砂岩试样均取自同一完整岩块.现场对岩块进行粗加工后运至室内实验室,经钻孔、切割、打磨后,最终制得直径50 mm、高100 mm的标准圆柱试样.试样尺寸误差严格按照《水力水电岩石试验规程》执行,上下断面误差应在±0.005 mm范围内.制备好的部分试验试样见图1.

图1 砂岩试样
试验方法:首先将轴压和围压以相同的加载速率(0.1 MPa/min)同时加载至预定值,待围压达到预定值后,保持不变,轴向应力施加方法改为位移控制模式,加载速率为0.02 mm/min,继续施加轴向荷载至试样失稳破坏,提取试验数据,取出破坏试样拍照记录,最后清理试验台进行下一组试验.根据隧道实际埋深情况,本文拟设置围压分别为30、40、50、60 MPa,以此来揭示高围压作用下隧道围压的力学特性.
2 试验结果分析
图2为围压30 MPa和60 MPa下砂岩三轴压缩应力-应变曲线.从图中可以明显看出:不同围压下砂岩的应力-应变曲线的变化规律大体相同;随着围压的增大,试样的峰值强度、峰值应变及弹性模量均呈逐渐递增趋势,峰后曲线逐渐由应变软化向应变硬化过渡,试样逐渐由塑性转变为岩性.以围压30 MPa应力-应变曲线为例,砂岩三轴压缩破坏大体可分为6个阶段:微裂隙压密阶段、弹性阶段、裂隙稳定扩展阶段、裂隙不稳定扩展阶段、峰后阶段和残余阶段.以围压5 MPa为例,不同阶段划分情况见图2(a).

(a) 围压30 MPa
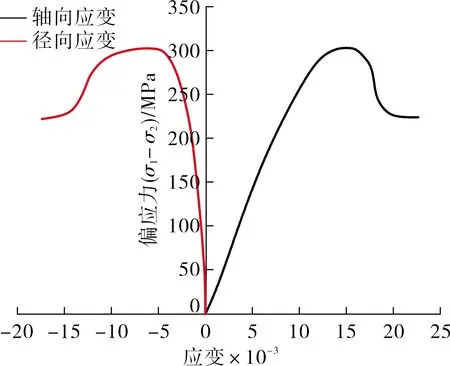
(b) 围压60 MPa图2 砂岩三轴压缩应力-应变曲线
微裂隙压密阶段I (OA):在加载初期,试样内部原始微裂隙、微缺陷逐渐被压密闭合,试样内部孔隙逐渐减少,致使应力-应变曲线呈上凹型变化,该阶段内径向变形几乎为零.
弹性阶段II (AB):该阶段内应力-应变曲线表现为明显的线性关系,即二者之间满足虎克定律,该阶内无新增裂隙产生.
裂隙稳定扩展阶段III (BC):当轴向荷载达到试样的起裂应力时,试样开始进入裂纹稳定扩展阶段,该阶段内,新生裂隙与闭合裂隙保持平衡,应力-应变继续保持线性关系.
裂隙不稳定扩展阶段IV (CD):当轴向荷载达到试样的扩容应力时,试样开始进入裂纹稳不定扩展阶段,该阶段内,新生裂隙增长速率开始大于闭合裂隙,应力-应变曲线转变为非线性的上凸型,试样内部开始逐渐连接贯通,且该阶段内径向应变开始快速增大.
峰后阶段V (DE):当轴向荷载达到峰值强度后,应力-应变曲线迅速跌落,试样瞬间失稳破坏,由于高围压作用,试样具有较高的残余强度.
残余阶段VI (EF):当轴向荷载随轴向应变的增长近似保持不变时,试样进入残余阶段,在高围压作用下,破坏试样仍具有一定承载能力.
为更加直观地对比分析不同围压下砂岩的应力应变-曲线之间差别,将不同围压下的偏应力-轴向应变曲线同时绘于图3中.从图中可以看出,随着围压的逐渐增大,试样的峰值强度、弹性模量、峰值应变和残余强度均呈逐渐增大趋势.根据试验数据计算砂岩的力学参数见表1.
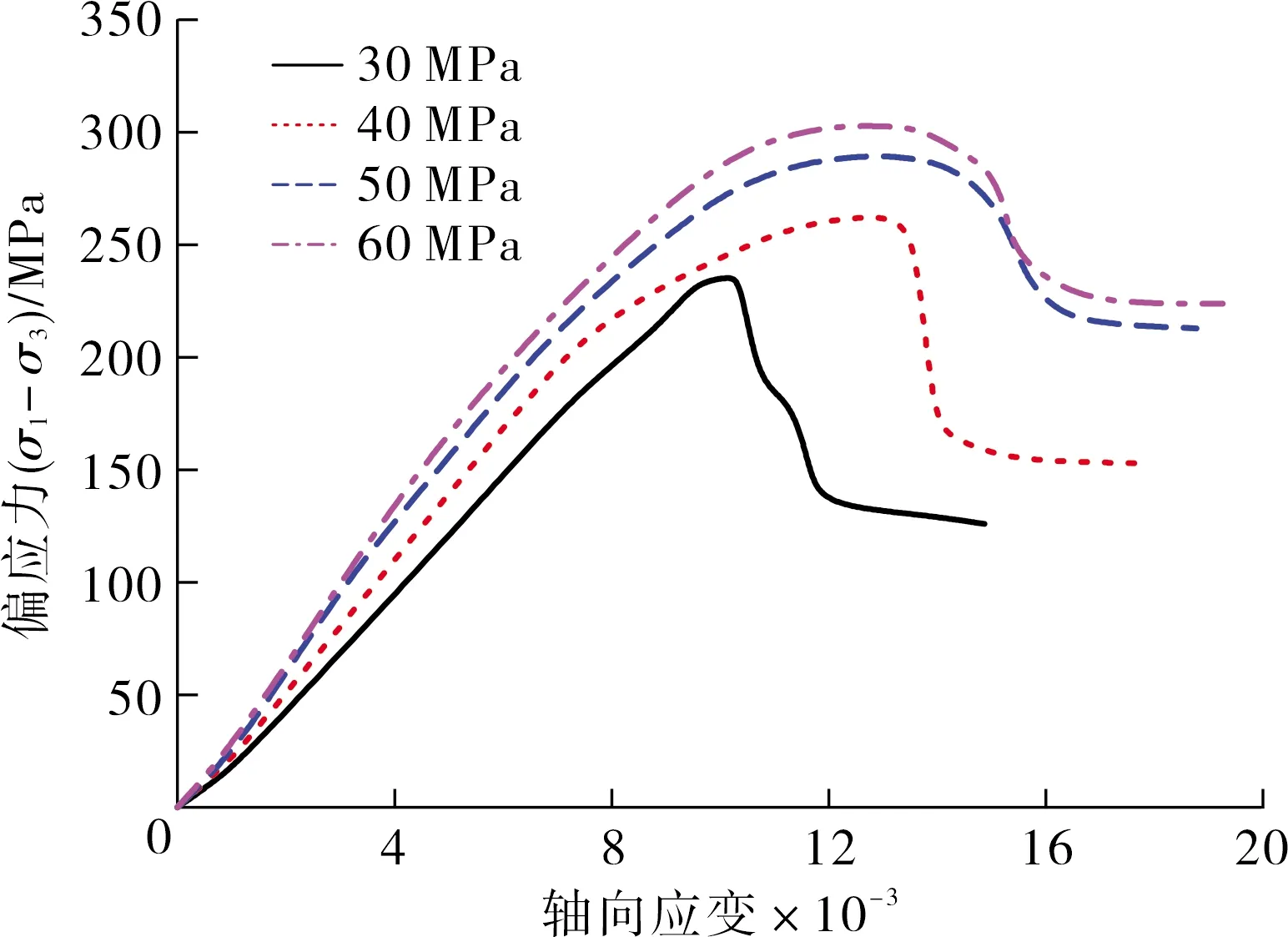
图3 不同围压下砂岩偏应力-轴向应变曲线
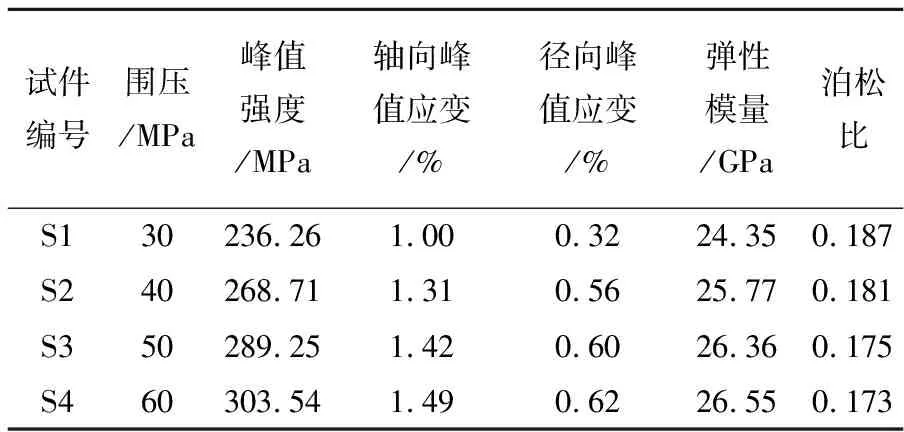
表1 试验结果
由表可知,试样的峰值强度、弾性模量、轴向峰值应变、径向峰值应变均随围压的增大而逐渐增大,泊松比则随围压的增大而逐渐减小,这一点与前文得到的结论相同.当围压为30 MPa时,砂岩的峰值强度为236.26 MPa、轴向峰值应变为1.00%,径向峰值应变0.32%,弹性模量为24.35 GPa、泊松比为0.187,当围压分别为40、50、60 MPa时,砂岩的峰值强度分别增长了10.41%、18.32%和22.17%,轴向峰值应变分别增长了23.66%、29.58%和32.89%,径向峰值应变分别增长了42.86%、45.76%和48.39%,弹性模量分别增长了5.51%、7.63%和8.29%,泊松比则分别减小了3.31%、7.47%和10.65%,可见,围压对砂岩力学参数的影响程度依次为:峰值应变>峰值强度>弹性模量>泊松比.
根据表中数据,绘制砂岩各力学参数随围压的分布曲线如图4所示.采用Origin软件对各力学参数随围压的分布曲线进行拟合,发现各力学参数与围压之间均满足指数函数关系,拟合参数均在0.95以上,表明各力学参数与围压之间具有较强的相关性.从图中还可以看出,随着围压的逐渐增大,各力学参数与围压之间的拟合曲线逐渐趋缓,拟合曲线斜率逐渐减小,表明高围压作用下各力学参数受围压影响程度逐渐减弱.原因是岩石试样在围压作用下,内部原始孔隙被压密闭合程度,进而导致岩石材料更加致密均匀,因此在相同轴向应力作用下其变形越小.但当围压增大至一定程度后,内部孔隙已被充分压密,继续增大围压后试样的压缩变小逐渐减小,因此各力学参数变化曲线随着围压的升高逐渐趋缓.
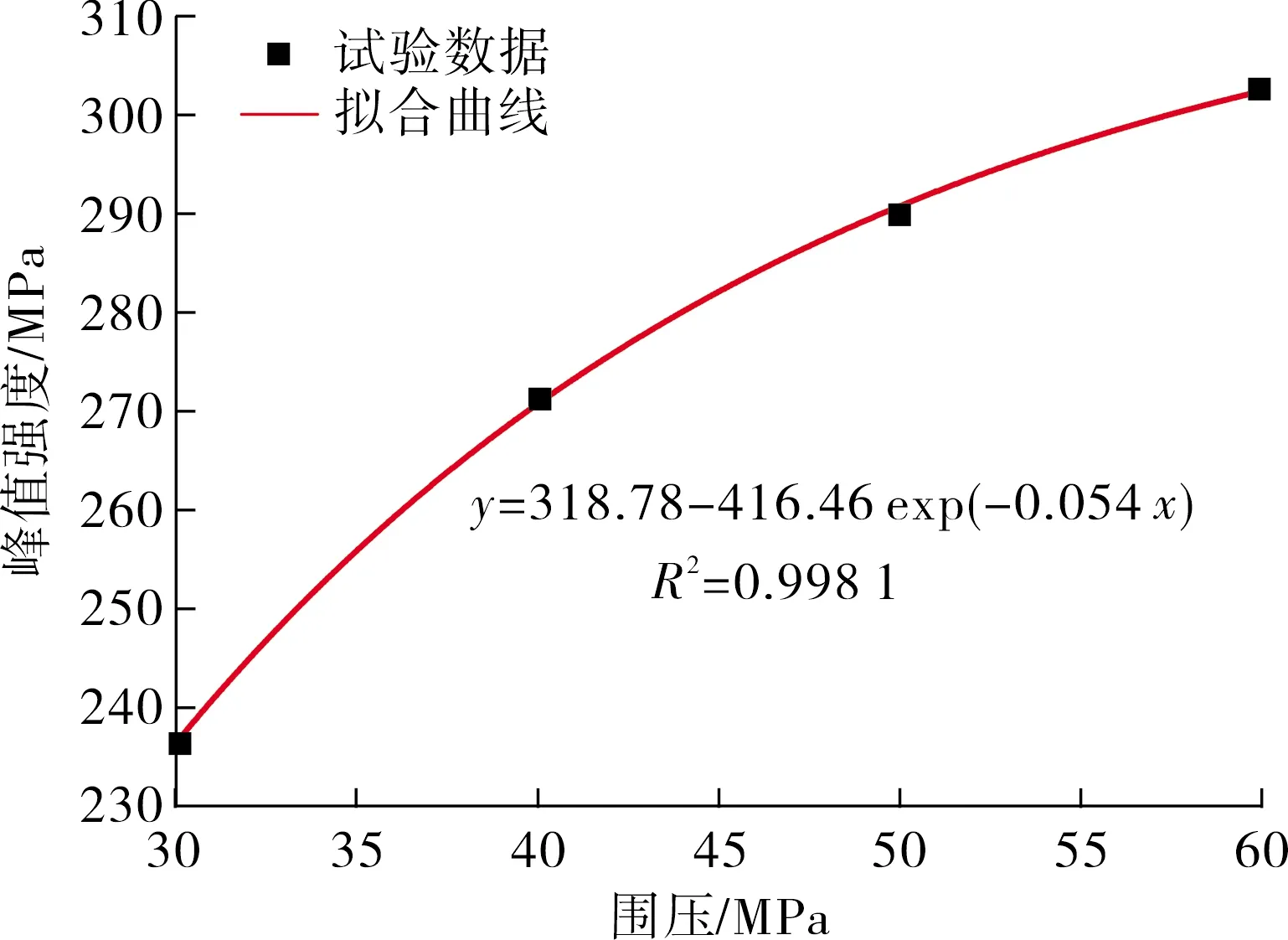
(a) 峰值强度
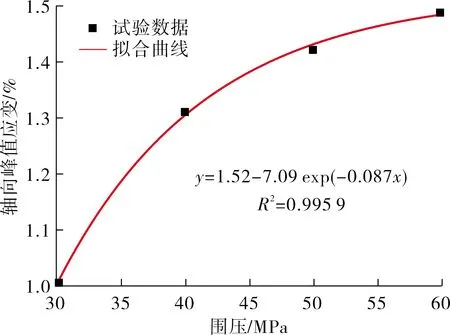
(b) 轴向峰值应变
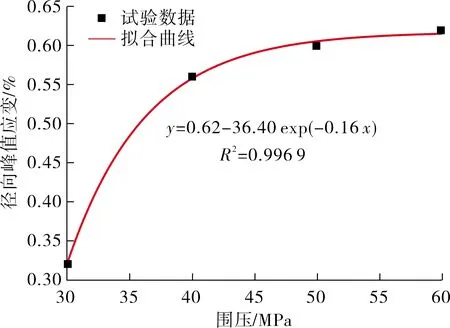
(c) 轴向峰值应变
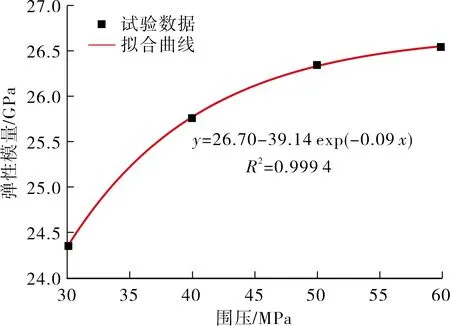
(d) 弹性模量
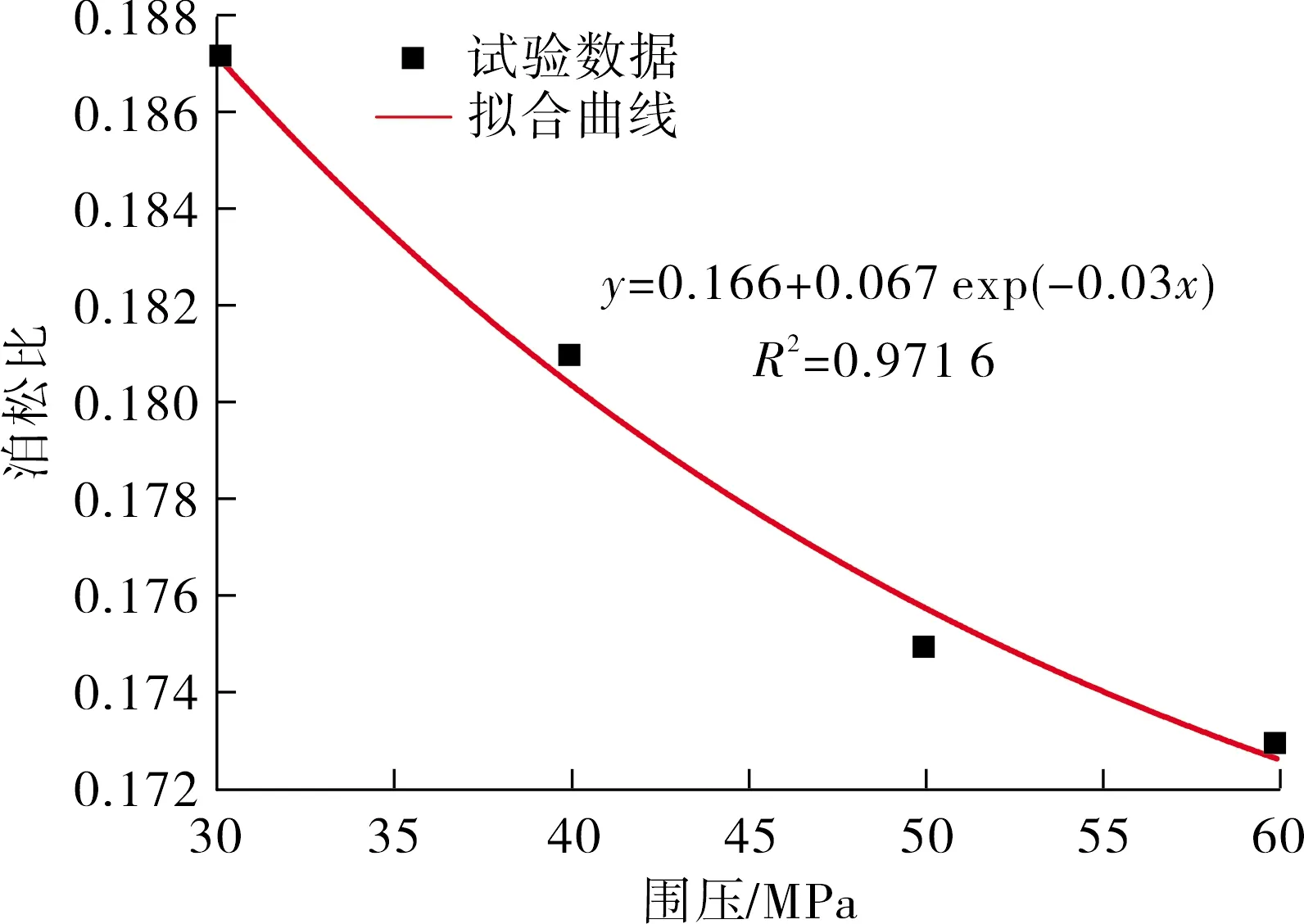
(e) 泊松比图4 砂岩力学参数与围压之间关系
3 结语
在较高围压作用下,砂岩应力-应变曲线变化趋势与低围压下基本相同,随着围压的逐渐增大,砂岩各力学参数均随围压呈规律性变化,在高围压下,各力学受影响程度依次为:峰值应变>峰值强度>弹性模量>泊松比.采用Origin软件对各力学参数随围压的分布曲线进行拟合,发现各力学参数与围压之间均满足指数函数关系.

