基于地下水动态模拟的生态输水累积效应

薛联青，廖淑敏，刘远洪，魏 卿，符芳兵

(1.河海大学水文水资源学院，江苏 南京 210098；2.石河子大学水利建筑工程学院，新疆 石河子 832003;3.济宁市水务综合执法支队，山东 济宁 272000)

自20世纪70年代大西海子水库建成后，塔里木河下游河道断流，不合理的水资源开发和极端干旱气候加剧了生态环境恶化[1-3]。为改善塔里木河生态环境，自2000年起进行间歇性生态输水，至2018年1月输水总量达70亿m3[4]。塔里木河下游植被得到恢复，地下水埋深抬升至6 m以上[5-6]。国内外有关地下水对生态输水的响应研究多集中在模型建立、地下水运动方程的开发上[7-9]，对输水带来的累积效应研究有待进一步加强。认识输水对地下水的累积效应可为输水策略的中长期规划提供科学指导，对节约干旱区水资源和塔河下游生态环境的恢复重建具有重要意义。

本文基于塔里木河下游2011—2017年进行的第12～18次生态输水，建立阿拉干断面局部三维地下水数值模型模拟7次间歇性输水条件下地下水的时空分布格局，明晰间歇性输水对地下水的有效影响范围，评估现有生态输水对地下水产生的累积效应，确定输水对地下水恢复的有效影响范围。

1 数据来源及模型建立

塔里木河下游大西海子水库以下共有英苏、老英苏、博孜库勒、喀尔达依、阿拉干、依干不及麻、库尔干和台特玛湖8个监测断面，其中，英苏和喀尔达依监测断面位于其文阔尔河河道，老英苏、博孜库勒监测断面位于老塔里木河河道，阿拉干监测断面位于两河道交汇处。由于各监测断面所处的地形地势有较大差别，只有分区构建模型才能较为准确地模拟塔里木河下游的地下水动态变化。以平原区的阿拉干监测断面为例，根据阿拉干监测断面的水文地质条件，利用实测地下水位数据和水文气象资料，以ArcGIS 10.4和GMS 10.4.5为工具，对2011—2017年第12～18次输水期间地下水在阿拉干断面的非稳定运动的状态进行模拟。

1.1 数据来源

1.1.1 气象水文数据

2001—2019年铁干里克气象站的逐日数据集合从中国气象数据网(http://data.cma.cn/)下载，包括降水量、平均风速和蒸发皿蒸发等。生态输水量来自大西海子水库下泄水量，研究区有2条支流——北侧的其文阔尔河(约185 km)和南侧的老塔里木河(约145 km)，2条支流在阿拉干监测断面处汇合，最终注入台特玛湖。生态输水数据由新疆塔里木河流域管理局提供。地下水数据使用的是塔里木河管理局提供的2011年1月至2017年12月各监测断面生态监测井每隔4 h记录一次的地下水埋深数据。

1.1.2 地质高程数据

输水过程中对地表水、地下水、植被响应等进行了野外监测，并对模拟区域开展了相关水文地质调查工作。模型建立采用的空间分辨率为30 m×30 m的ASTER GDEM数字高程数据来源于地理空间数据云，是目前唯一覆盖全球陆地表面的高分辨率高程影像数据。

1.2 地下水数值模拟模型

MODFLOW是模拟和预测地下水状况以及地下水/地表水相互作用的国际标准模型，被广泛应用于建立三维地质模型，模拟地下水运动。GMS(groundwater modeling system)是模拟地下水水环境的软件系统，支持USG、LGR、NWT、2000、2005等MODFLOW版本。

1.2.1 间歇性输水下局部地下水模拟

1.2.1.1 概念模型导入有限差分模型

由于河流双侧地下水的对称性及模拟区域的典型性，模拟区域的边界以典型平原区断面阿拉干监测断面处的河道为中心，向河道两侧各扩展5.0 km，由ArcGIS裁剪缓冲区。该区域包含老塔里木河(河道长度19.29 km)、其文阔尔河(河道长度15.97 km)、塔里木河(河道长度14.38 km)，为不规则区域，如图1所示。该区域有6个生态监测井(H1、H2、H3、H4、H5和H6)，距离河道右岸垂直距离分别为50 m、150 m、300 m、500 m、750 m和1 050 m。

图1 塔里木河下游模拟区域示意图Fig.1 Sketch map of simulated area in the lower Tarim River

a.边界条件设置：模拟区域取自距河道两侧5 km、距阿拉干监测断面两侧5～7 km的流域，输水对河道两侧5 km外的区域影响甚微[10]，将模拟区域的四周边界线概化为通用水头边界(GHB)，模拟区域内的河道在过水时均被概化为第三类边界[11]。

b.高程数据插值：选择自然邻域法进行插值。

c.初始水位计算[12]：2010年12月底的水位应作为模型模拟的初始水位，由于2010年11月12日至2011年1月6日没有进行输水，2011年1月初的水位与2010年12月底水位并无明显差异，取2011年1月1日监测井平均地下水埋深6.5 m计算的地下水位作为初始水位。

1.2.1.2 模拟区域水文地质条件概化

由于整个塔里木河下游的地下水纵向运动滞缓且与河道走向一致[13]。概化的大厚度潜水含水层垂向厚度取为40 m，分为4层。塔里木河下游滩槽高差1～3 m，河床宽约20～30 m，坡度约1∶4 500至1∶7 500[14]。根据各含水层的岩性、导水性和相关试验，对模拟区域参数赋初始值。结合已有研究与试验[11,13-14]，模拟区域水平渗透系数取2.5 m/d，垂直渗透系数取2 m/d；水平各向异性系数取2.0；单位储水量取0.000 1/m；给水度取0.24。模拟区域331.5 km2，由GMS自动生成250 m×250 m正方形网格，有效单元格5 304个。模拟时间为2011年1月1日至2018年1月4日，共2 561 d，应力期根据输水期进行划分，分为22个应力期。

1.2.1.3 源汇项计算

研究区域多年平均潜在蒸散发量约为多年平均降水量的70倍[15-16]，降水在入渗补给地下水前就已消耗殆尽，垂向的补给为输水期河道的渗漏。模拟区域远离居民聚集地，无农业生产生活用水，仅考虑河道补给。主要排泄方式为潜水蒸发、植被蒸腾和地表水蒸发[17]，由于模拟期间阿拉干监测断面的地下水埋深小于4.5 m，此时潜水蒸发趋近于零，实际蒸散发采用基于互补相关理论的平流-干旱模型进行计算。河流数字化后提取河道高程，输入如表1所示的断面流量作为河道流量。

1.2.2 不同应力期最大蒸散发速率

根据铁干里克水文站的实测日气象数据，采用基于互补相关理论平流-干旱模型[18]计算铁干里克站2011—2019年实际蒸散发量[19]。不同应力期的最大蒸散发速率按照距离河道远近进行赋值[20]。

(1)

(2)

(3)

式中：Ep——潜在蒸散发量；Ew——湿润环境蒸散发量；Ea——实际蒸散发量；Δ——温度-饱和水汽压曲线斜率；Rn——地表净辐射；G——土壤热通量；γ——干湿表常数；α——经验系数；E——充分供水时的实际蒸散发量；e——水汽压；Eab——干燥力。Ep通过EToClaculator计算，G≈0，Δ、Rn、γ、e、Eab参数的详细计算见文献[18，21]。

1.2.3 参数调整及灵敏度分析

监测井水位观测值、模拟值见图2。监测井H1、H2、H3、H4、H5和H6的观测水位和模拟水位的平均误差σ分别为0.36 m、-0.27 m、-0.42 m、0.56 m、0.65 m和0.05 m，均方根误差分别为1.097 m、0.418 m、0.389 m、0.620 m、0.787 m和0.328 m。其中，H2、H3模拟水位比实测水位低，H4、H5模拟效果较差，H6模拟效果最好，整体模拟结果可行，模型识别比较成功。

图2 阿拉干监测断面监测井观测水位与模拟水位对比Fig.2 Simulation level and monitoring level comparison of monitoring wells in Alagan section

为对已识别过模型的不确定性进行量化，需要对模型参数进行灵敏度分析。分别对河道水位Hr、水平渗透系数KH、垂直渗透系数KV、给水度SY、单位储水量SS和水平各向异性系数A这6个参数进行分析，取参数增加、减少20%和10%分别与参数无变化时的地下水位做比较，对地下水位变化量取绝对值绘制监测井的水位变幅，如图3所示。由图3可知，大幅度的参数变化对地下水变化影响较小，变幅20%时水位变化量小于0.4 m，采用的水文地质参数可用于地下水数值模拟。

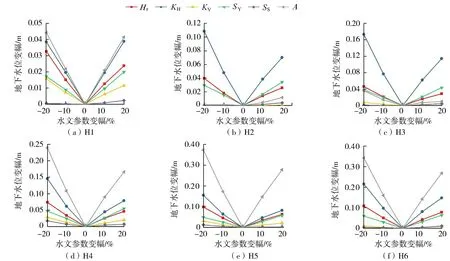
图3 参数变化下各监测井地下水位变幅Fig.3 Variation amplitudes of groundwater level of each monitoring well under different parameters

2 生态输水对地下水的累积效应

输水对阿拉干断面地下水的累积效应通过地下水输水前后的时空响应规律揭示，通过含水层等水位线时空分布格局和地下水变化量时空分布格局分析地下水的响应范围，包括地下水距河道的响应距离和受水面积。为表达方便，将老塔里木河河道称作南侧河道，其文阔尔河河道称作北侧河道，塔里木河河道称为塔河河道。

2.1 地下水距河道的响应距离

运行所得模拟区域的含水层等水位线分布如图4所示，图中的日期选择输水前一天和输水最后一天。等水位线越密集表示水位变化较快，输水补给作用强烈；越稀疏表示水位变化缓慢，输水补给作用弱化。对模拟的7次输水来说，输水前后地下水位基本以河道为中心，向河道两侧递减，形成以河道为脊的分水岭。

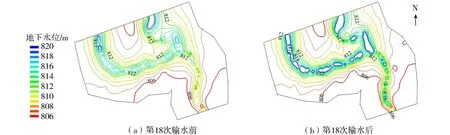
图4 第18次输水前后含水层等水位线分布Fig.4 Water level distribution of water aquifer before and after 18th ecological water conveyance

输水后南北河道两侧1 000 m的响应距离内地下水位抬升1～2 m(表2)，地下水位为812 m、814 m、816 m距河道的最大响应距离分别为1 100 m、800 m、600 m(表3)。随着输水的持续进行，地下水的抬升幅度和抬升范围均有增大，输水前的高水位覆盖范围也逐渐扩大，体现在高水位等水位线距河道宽度变大，范围扩大，直观地展示了输水带来的累积效应，如图4所示。

表2 输水前后距河道不同距离的地下水位及其抬升量

表3 输水后地下水的有效响应距离 单位：m

值得注意的是，由于河道渗漏和蒸散发影响，两河交汇处的塔里木河在模拟区域下游尽头由河道损耗导致的水位降低十分明显，输水后812 m以上的地下水距河道的响应距离分布在距河道两侧400～1 000 m内，816 m以上的地下水距河道的响应距离分布在距河道两侧150～500 m内，越靠近尾闾湖范围越小。由多阶段(第12、14、18次)输水结果得知，由于Ⅰ阶段河道过水补充了含水层且输水间隔小于2个月，减缓了后续阶段输水前地下水位的下降，说明小间隔多阶段的持续输水可以保持地下水位有效抬升，也能继续维持地下水的有效响应距离。

2.2 地下水受水面积

由图5可知，第18次输水后，低水位(低于807 m的水位)的受水面积由250.1 km2缩减至127.0 km2，减少了49.22%；中水位(介于807～813 m的水位)受水面积由81.4 km2增加至151.8 km2，增长了86.49%；高水位(高于813 m的水位)受水面积由0增加至52.7 km2。地下水低水位受水面积减小，中高水位受水面积增大，中水位受水面积逐渐超过低水位受水面积，占模拟区域的45.78%。第12次Ⅰ阶段输水后中高水位受水面积为低水位受水面积的0.32倍，第18次输水后中高水位受水面积达到低水位受水面积的1.61倍。

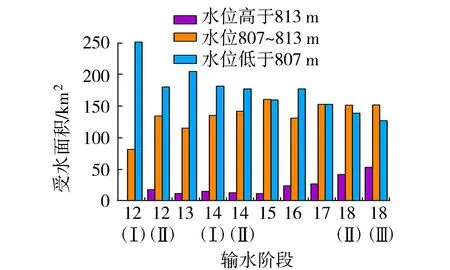
图5 输水后不同区间地下水的 受水面积变化Fig.5 Variation of affected areas of groundwater in different zones after water conveyance

2.3 地下水位变化量

为量化输水后地下水位变化幅度、变化范围，由图4得到输水后相对输水前地下水位变化量，变化量构成的等值线沿河道对称分布，河道附近的变化量等值线与输水后含水层等水位线图所展示的等水头线分布高度重合。模拟期的地下水位变化量在-2～6 m以内，其绝对值呈距河道由近及远逐渐减小的规律。

表4为各阶段输水后与输水前地下水位变化量距河道的响应距离，由表4可知，多阶段输水的第12、14、18次输水的第一阶段地下水位变化量为1～3 m，距河道最大响应距离由第12次输水的300 m增加至第18次输水的600 m；第二阶段地下水位变化量增加至1～4 m，距河道最大响应距离可达1 100 m，响应距离比第一阶段扩大。地下水位变化量距河道的最大响应距离呈波动性减小，累积效应对地下水的最大有效影响范围有所收窄，是由于随着输水量的累积地下水位逐渐抬升至趋于稳定状态，累积效应变化速率由大到小逐渐趋于稳定。

表4 输水后地下水位变化量距河道的响应距离

3 结 论

a.模型对阿拉干断面的地下水位模拟效果较好，平均误差为 0.162 m，平均均方根误差 0.607 m，水文参数合理，能够用于间歇性输水条件下的地下水模拟。

b.阿拉干断面含水层地下水等水位线时空分布格局呈现明显的以河道为中心，向河道两侧递减，形成以河道为脊的分水岭特点。

c.累积效应对地下水的有效影响范围包括地下水的响应距离、受水面积2个指标：输水后 812 m以上的地下水距河道的响应距离分布在距河道两侧 400～1 100 m内；第18次输水后中高水位受水面积是低水位受水面积的1.61倍；输水的有效响应距离主要分布于距河道 1 000～2000 m范围内。