冷弯薄壁矩形管板组相关屈曲压弯承载力研究

邓露，龙砺芝，刘艳芝，何钰龙

摘   要：冷弯薄壁矩形钢管柱易发生局部屈曲破坏. 为了研究冷弯薄壁矩形钢管柱的压弯承载性能，建立并验证了冷弯薄壁矩形钢管柱非线性有限元模型. 采用上述模型对不同轴压比、翼缘宽厚比及腹板宽厚比的884个受常轴压力、变水平力作用的矩形钢管柱进行参数分析，研究了构件承载极限状态的截面破坏形式和抗弯承载力. 结果表明：冷弯薄壁矩形钢管柱绕强轴压弯过程主要出现两种破坏模式，比如：全截面屈服和受压翼缘与腹板屈曲. 结合极限状态的应力分布特征，基于有效塑性宽度法提出了考虑板组相关屈曲的冷弯薄壁矩形钢管柱的极限抗弯承载力计算公式，其预测值与有限元模拟结果吻合良好.

关键词：板件相关作用;局部屈曲;抗弯承载力;冷弯薄壁;矩形截面钢管柱

中图分类号：TU338                              文献标志码：A

Research on Compression-bending Capacity

of Cold-formed Thin-walled Rectangular Tube Considering

Interactive Buckling of Plate Group

DENG Lu1，2，LONG Lizhi1，LIU Yanzhi1，HE Yulong1

（1. College of Civil Engineering，Hunan University，Changsha 410082，China;

2. Key Laboratory of Building Safety and Energy Efficiency（Hunan University），Ministry of Education，Changsha 410082，China）

Abstract：Cold-formed thin-walled rectangular steel tube columns are prone to local buckling failure. In order to study the compression-bending capacity of cold-formed thin-walled rectangular steel tube columns， a nonlinear finite element model of cold-formed thin-walled rectangular steel tube columns was established and verified. This model is used to simulate 884 rectangular steel tube columns with different axial compression ratios， flange width-thickness ratios， and web width-thickness ratios under constant axial pressure and variable horizontal forces， and the failure mode and flexural capacity in the ultimate limit states are examined. The results show that there are mainly two failure modes in the compression-bending process of cold-formed thin-walled rectangular steel tube columns in the strong axial： full-section yield， and compression flange and web buckling. Combined with the stress distribution characteristics of the limit state，a calculation formula for the ultimate flexural capacity of cold-formed thin-walled rectangular steel tube columns considering the relative buckling of the plate group is proposed based on the plastic effective width method. The predicted value is in good agreement with the finite element simulation results.

Key words：related effects of plates;local buckling;flexural capacity;cold-formed thin-wall;rectangular section steel tube column

冷彎薄壁型钢构件因具有轻质、高强、易装配等优点而被广泛应用于低层建筑，且近年来逐步从低层向多层建筑发展[1]. 因其受压性能好、抗弯刚度较大，冷弯薄壁矩形钢管柱广泛用于多层框架柱结构抗侧力构件. 然而，冷弯薄壁矩形钢管柱的板件宽厚比一般较大，易发生局部屈曲，削弱了构件的极限承载力. 因此，局部屈曲是研究冷弯薄壁型钢构件极限承载性能的重点问题之一.

关于冷弯薄壁型钢板件局部屈曲的问题，国内外研究较为成熟. 多板件组合的冷弯薄壁型钢构件（T形、H形以及矩形等构件）在实际工程中应用广泛，然而该类构件的局部屈曲问题往往要考虑板件之间的相关性[2-3]. 邓长根等[4]研究表明焊接H形截面钢构件的极限弯矩比随翼缘宽厚比和轴压比增大而明显减小. 曾锋[5]研究表明冷弯薄壁矩形钢管柱轴压承载力相对较弱的腹板轴压承载力提高约12%，而相对较强的翼缘板轴压承载力会降低.

然而，钢结构规范GB 50017—2017《钢结构设计标准》[6]对构件截面进行分类时，往往将截面的腹板、翼缘简化为四边简支单板，未考虑极限状态下翼缘和腹板之间的约束关系. GB 50018—2002《冷弯薄壁型钢结构技术规范》[7]采用板组约束系数来考虑构件极限状态下板件的相关屈曲作用，从而计算截面有效宽度，设计过程复杂，较为不便. Cheng等[8- 9]基于Chen 等[10]提出的有效塑性宽度法，考虑了板件相关作用，拟合了一个能够准确预测H形截面构件抗弯承载力的公式. 但该方法是否适用于冷弯薄壁矩形截面压弯钢构件极限抗弯承载力的计算，还有待验证.

考虑板组相关屈曲对冷弯薄壁矩形钢管柱抗弯承载力的影响，本文对不同翼缘宽厚比、腹板宽厚比以及轴压比组合下的冷弯薄壁矩形钢管柱的极限抗弯性能进行数值模拟及理论研究. 采用文献[11]试验数据验证本文建立的冷弯薄壁矩形压弯构件非线性有限元模型. 随后对不同翼缘宽厚比、腹板宽厚比及轴压比组合下矩形截面钢构件的单调压弯过程进行参数分析，研究各参数组合对极限承载力的影响机理，并基于有效塑性宽度法的计算原理拟合适用于冷弯薄壁矩形钢管柱的极限抗弯承载力计算公式.

1   数值模型

1.1   加载模式

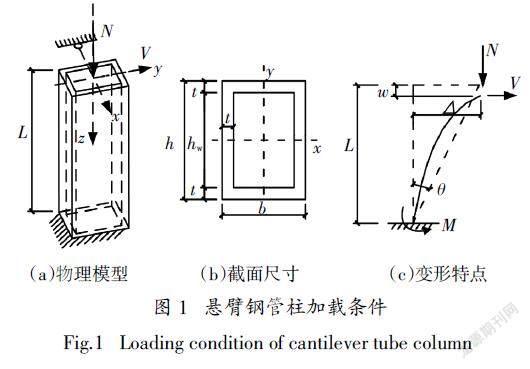
冷弯薄壁型钢管框架柱属于压弯构件，所承受的轴力基本不变，而弯矩时常变化. 因此，根据其工作机理，取反弯点处一半作为分析模型，可简化为受恒定轴力与水平力作用下的冷弯薄壁矩形悬臂钢管模型. 本文只考虑局部屈曲对构件抗弯承载力的影响，选取长细比较小的短柱，长度L为1 000 mm，以保证构件不发生平面外整体失稳破坏. 在悬臂短柱自由端施加常轴力N和水平力V. 水平加载通过绕强轴方向的水平位移控制，直至构件完全破坏时停止加载. 悬臂钢管柱的物理模型、截面尺寸以及变形特点见图1.

1.2   数值分析模型与验证

采用有限元软件ABAQUS模拟冷弯薄壁矩形钢管柱绕强轴压弯过程的非线性行为. 采用4节点四边形的壳单元S4R，网格密度划分为10 mm×10 mm×40 mm，沿翼缘和腹板布种间距为10 mm，沿构件长度布种间距为40 mm. 材料模型取三线性应力-应变模型[11]，材料选用Q235钢材，弹性模量E为210 GPa，塑性模量E′取0.02E，屈服应力σy为310 MPa，极限应力σ′为400 MPa，屈服应变εv为0.15%，极限应变ε′为2.3%，泊松比为0.3. 边界条件：底端限制三个方向的位移和旋转;顶端约束x方向上的位移，以防止试件沿x方向偏移. 施加沿y轴方向的水平变荷载和沿z轴方向的恒定竖向荷载，模拟钢管柱的压弯状态. 有限元模型如图2所示.

本文研究短柱构件，不考虑整体屈曲，对于局部初始缺陷，取构件局部屈曲的一阶模态[12]作为几何初始缺陷模态，局部鼓曲峰值取W/150[13]，W为截面腹板宽度. 冷弯薄壁型钢构件的冷弯残余应力可忽略不计[14].

Yang等[11]完成了一系列厚度低于3 mm的冷弯薄壁矩形截面悬臂足尺构件的拟静力试验.本文通过该试验结果验证有限元模型，材料强度取其材性试验的实测值. 其中R1、R2以及R3为冷弯薄壁矩形截面钢管悬臂柱，其腹板高度为160 mm，翼缘宽厚为80 mm，板件厚度为2.49 mm. 作用在试件R1的轴压力为33 kN（轴压比为0.1），作用在试件R2的轴压力为66 kN（轴压比为0.2），作用在试件R3的轴压力为99 kN（轴压比为0.3）. V为作用在自由端的水平推力，δ为构件水平位移. 各试件在达到极限承载力时，ABAQUS与试验得到的破坏模式比较如图3所示，两者破坏模式基本一致. ABAQUS和试验获得的骨架曲线和滞回曲线分别在图4、图5进行了比较. 比较表明，有限元模型能够较好地模拟构件的极限承载力性能和构件达到极限承载力后的刚度退化性能，且有限元模型计算得到的水平极限荷载与试验接近，误差在5%以内. 因此采用本文有限元建模方法进行参数分析是可行的. 基于已验证的数值模型，选取翼缘宽厚比、腹板宽厚比以及轴压比3个参数，研究冷弯薄壁矩形钢管柱在不同截面尺寸及不同荷载条件下的板组相关屈曲的极限承载性能.

2   板组相关屈曲分析

2.1   参数选择与组合

板件宽厚比与轴压比是影响冷弯薄壁矩形钢管柱绕强轴压弯极限承载性能的主要因素[3]. 用rf、rw分别标记翼缘、腹板相对宽厚比，n为轴压比.

rf = b/t     （1）

rw = h/t     （2）

n = N/[2tfy（b + h）]     （3）

式中：fy为板件的屈服强度;N为轴压力;t为板件厚度;b、h分别为矩形钢管截面的宽度和高度.

本文研究对象是宽厚比较大的冷弯薄壁矩形钢管柱，板件厚度t不变，通过改变截面翼缘、腹板宽度控制板件翼缘宽厚比和腹板宽厚比. 翼缘宽厚比rf取35～59，每间隔1.5取一个值，共计17个值，腹板宽厚比rw取60～120，每间隔5取一个值，共计13个值，轴压比n取0.1、0.2、0.3、0.4. 通过所选的rf、rw和n进行组合，共计884个分析模型，囊括了3个截面等级的大部分情况. 各模型以R-n-rf-rw命名，如R-0.1-35-60表示n = 0.1，rf = 35，rw = 60的构件.

2.2   破坏模式与相关屈曲分析

所选构件中部分构件绕强轴压弯破坏过程中出现局部屈曲，试件翼缘及腹板底端出现严重的局部屈曲变形. 局部变形主要表现为平面外的位移突变，本文以板件平面外位移的突变作为局部屈曲发生的标志. 压弯钢构件极限状态的破坏模式分为两类：第一类，全截面屈服（图6（a）），當翼缘宽厚比较小时，受压翼缘和受拉翼缘均屈服，塑性在腹板开展充分，腹板受拉区和受压区均进入屈服状态，只有腹板中性轴附近未开展塑性，始终保持在弹性状态;第二类，受压翼缘与腹板屈曲（图6（b）），当翼缘宽厚比或腹板宽厚比较大时，较弱板件的局部屈曲变形牵制较强板件一起屈曲. 在达到极限承载力时，大部分腹板区域屈曲失效，构件沿腹板截面高度的塑性开展深度明显减少，严重削弱构件的承载力.

通过Python脚本提取ABAQUS参数分析范围内所有构件的极限弯矩Mu，并与塑性弯矩Mpc相比进行无量纲化. 塑性弯矩Mpc[8]通过假定极限状态轴压力产生的压应力主要分布在腹板中和轴附近的应力分布形式计算所得. 将无量纲值列于图7，当n、rw恒定，Mu /Mpc随着rf增大而减少. 当Mu /Mpc≥1，构件在极限状态时，全截面均能达到屈服强度，发生第一类破坏;当Mu /Mpc<1，构件在极限状态发生局部屈曲，极限弯矩小于塑性弯矩，属于第二类破坏模式.

通过各阶段板件平均应力的大小和分布可对上述模式的产生过程进行具体分析. 平均应力[9]是指沿板件厚度方向上内外表面应力的平均值. 板件屈曲前，受压区的压应力沿板件厚度方向几乎相同. 板件屈曲后，板件凸面由于受到拉伸变形，该处压应力减小，拉应力增大. 板件凹面受到挤压，该处压应力继续增大. 故屈曲后板件平均应力减小，承载力降低. 因此压弯构件破坏过程中板件平均应力的大小与分布对应着该阶段构件的抗弯承载力与变形.

本文所选构件中翼缘相对腹板为强板，且腹板在构件受弯过程起主要抗力作用. 冷弯矩形截面绕强轴压弯过程中，随着外荷载水平力的增大，在翼缘与腹板交接处附近的腹板最先达到屈服强度，随后截面塑性在翼缘或腹板上沿两端向中间逐渐开展. 当达到极限弯矩时，对于第一类破坏模式的压弯构件，此阶段翼缘平均应力沿宽度均匀分布，腹板平均应力沿腹板中心对称分布. 第二类破坏模式的构件在达到极限状态时，受压翼缘与腹板均屈曲，腹板中心段由于屈曲变形较大，平均应力基本为0，处于失效状态. 腹板和翼缘协同变形，受压翼缘中间部分屈曲变形，平均应力减小，可认为失效，退出工作状态. 由于腹板为弱板，腹板对翼缘的约束较小，与腹板交接处的受压翼缘在破坏过程中平均应力均较小，基本没有屈曲变形，可等效为翼缘有效宽度. 两种破坏类型的构件受拉翼缘在极限状态时均保持拉伸状态，其应力大小取决于屈曲翼缘及腹板的应力大小与分布.

图8选取构件R-n-120-35、R-n-120-59以及R-n-60-59，以分析腹板宽厚比rw、翼缘宽厚比rf以及轴压比n对构件板组相关性和极限抗弯承载力的影响. 其中n选0.1和0.4，θe为屈服旋转角，Mec为截面边缘屈服弯矩[8]，σu为平均应力. 研究构件R-n-120-35和R-n-120-59发现，当腹板宽厚比相同翼缘宽厚比不同时，翼缘宽厚比越大，翼缘对腹板的约束程度越小，构件屈曲越早，塑性开展越窄，翼缘有效宽度越小，故极限抗弯承载力越小. 当翼缘宽厚比相同腹板宽厚比不同时，比较构件R-n-120-59和R-n-60-59，可分析腹板宽厚比对构件极限抗弯承载力的影响. 主要体现在两个方面：第一、构件在达到极限弯矩之前，腹板宽厚比越大，腹板对翼缘约束作用越弱，受压区翼缘在极限状态下的有效宽度越小;第二、构件在达到极限弯矩后，腹板宽厚比越大，因屈曲变形程度越大，截面失效范围越大，Mu与Mec的比值越小，故构件极限抗弯强度退化越快. 轴压比越大，Mu /Mec越大. 总而言之，翼缘与腹板相关屈曲作用行为与其各自的宽厚比及轴压比紧密相关，从而影响构件的抗弯极限承载力.

3   抗弯承载力分析

3.1   有效塑性宽度法

有效塑性宽度的原理是根据构件截面极限状态的应力分布模式求取该状态下有效塑性截面的全塑性弯矩[10]. 冷弯薄壁型钢构件大多采用大宽厚比截面，易发生局部屈曲，国内规范常用有效宽度法计算构件的极限承载力，但过程繁琐、复杂. 因此，本文基于Chen等[10]提出的有效塑性宽度法，对冷弯薄壁矩形截面压弯钢构件在0 < n ≤ 0.4、35 ≤ rf ≤ 59、rw ≤ 120情况下的承载力分别进行计算.

3.2   Mu /Mpc = 1宽厚比限值

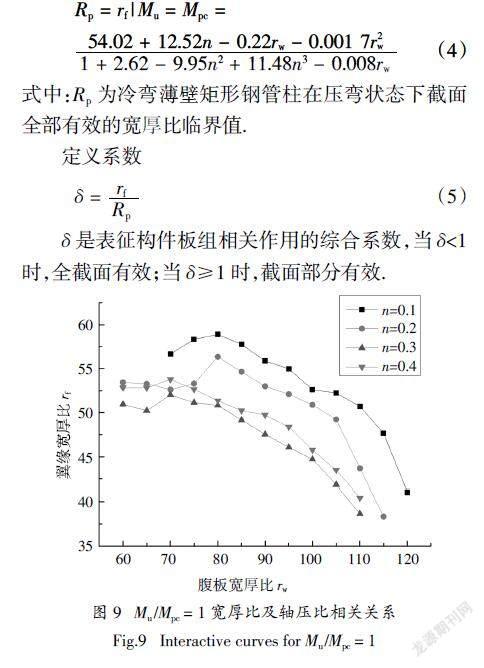
从图7选取各轴压比下Mu /Mpc = 1的rf与rw的数值，列于图9中（若参数分析点不通过Mu /Mpc = 1，采用插值法），拟合Mu /Mpc = 1的rf、rw与n的相关表达式，R2 = 0.962. 如下所示：

Rp = rf | Mu = Mpc =

■ （4）

式中：Rp为冷弯薄壁矩形钢管柱在压弯状态下截面全部有效的宽厚比临界值.

定义系数

δ = ■        （5）

δ是表征构件板组相关作用的綜合系数，当δ<1时，全截面有效;当δ≥1时，截面部分有效.

■

腹板宽厚比rw

3.3   有效截面尺寸

构件在极限状态下的有效截面宽度受rf、rw和n共同影响，因此本文选取表征三者相关关系的综合参数δ（板组相关屈曲系数），以计算板件有效宽度. 根据本文2.2节的分析，有效截面示意图如图10所示.

当δ≥1时，根据参数分析结果，可取翼缘有效宽度be=b/δ，腹板有效高度he=hw /■. 且当腹板宽厚较小时，需考虑其对翼缘的有利约束作用. 截面翼缘有效宽度be和腹板有效高度he的计算公式如下.

be = minb，■        （6）

he = minhw，■        （7）

3.4   考虑强化作用的翼缘应力及腹板应力

对满足δ<1的截面，达到极限状态时板件已达到全塑性，部分进入强化阶段，在计算极限承载力时，应考虑应力的强化作用. δ越小，板件越不易发生屈曲，达到极限状态时塑性发展程度越高. 因此定义强化参数μ = 1 + m（1 - δ），以考虑应力的强化作用，其中m为待定系数，m与材料强化阶段的塑性模量有关. 对于理想弹塑性材料m = 0，而针对本文的有限元材料模型，当m = 0.4时，计算所得的截面抗弯承载力与有限元结果吻合较好. 标记极限状态时翼缘和腹板应力为σu，表达式为：

σu = μ fy        （8）

μ = 1.5 - 0.4δ ≥ 1      （9）

式中：μ为应力强化系数，当不考虑强化作用时，取μ = 1.

局部屈曲对构件极限承载力有较大的削弱作用，且所选构件为薄壁钢构件，在达到极限承载力之前，塑性发展较小. 因此当δ ≥ 1时，不考虑材料的强化作用，σu取fy .

3.5   抗弯承载力计算公式

压弯钢构件在达到极限状态时，有效截面全部进入塑性，翼缘应力和腹板应力均为σu . 假定竖向荷载产生的轴向压应力集中分布在腹板及近腹板的翼缘处，当轴压比0 < n ≤ 0.4时，绕强轴矩形截面压弯钢构件的板件腹板宽度大于翼缘宽度，且壁板厚度相同，因而作用在该类构件上的轴压力产生的压应力可认为只分布在腹板. 根据力的平衡条件得：

Nq = tσu [（2he - 2ht） - （b - be） - 2ht]    （10）

式中：he为腹板有效宽度;be（be = be1 + be2）为翼缘有效宽度;ht为腹板受拉区有效宽度.

当N ≤ Nq时，轴压力产生的压应力只作用于腹板区域，有效截面的应力分布形式如图11所示.

所有正应力对形心轴x取矩，求得截面抗弯承载力为：

Mu=0.5（be+b）（h-t）tσu+2ht（hw-ht）tσu    （11）

本文针对长度（L）为1 000 m的悬臂钢管短柱，基于有效塑性宽度法，根据极限状态的应力分布特点，考虑轴压比0

4   抗弯承载力计算公式评估

随机抽取54个轴压比下不同翼缘宽厚比与腹板宽厚比组合的压弯构件，分别用有效塑性宽度法（Plastic Effective width Method，PEM）和GB 50018—2002薄壁规范计算极限承载力，并将计算结果以及ABAQUS有限元計算结果与边缘屈服弯矩的比值分别列于图12. 对比发现，该薄壁规范设计的压弯截面构件过于保守;PEM法计算结果与ABAQUS结果较为接近，通过误差分析可知，Mu，ABAQUS /Mu，PEM的平均值为1.019，变异系数为0.045，PEM法较为精确地计算该构件的极限抗弯承载力. GB 50018—2002薄壁规范对冷弯薄壁型钢构件没有明确的截面分类，截面的极限承载力设计均采用边缘屈服准则，不考虑各类薄壁截面的塑性作用. 虽然该薄壁规范采用有效宽度法通过引入腹板约束系数k1，以考虑板组相关屈曲作用对构件极限承载力的影响，但是其对于构件截面极限承载力的估计偏保守，且计算过程繁琐复杂. 而本文针对在压弯极限状态下全截面屈服的冷弯薄壁型矩形钢构件考虑其截面塑性作用以及对于截面部分屈服的构件，考虑其板组相关屈曲作用忽略其部分塑性发展，采用有效塑性宽度法计算构件极限承载力. 该方法根据截面极限状态应力分布模式表征构件极限状态的非线性性能，故能较为准确地估计截面的极限承载力.

5   结   论

基于本文已验证的有限元模型，对不同板件宽厚比与轴压比组合下的冷弯薄壁矩形钢管柱进行有限元非线性分析，研究了板组相关屈曲作用对构件极限抗弯性能的影响，得到以下主要结论.

1）压弯构件在承载极限状态下主要发生的两类破坏模式：全截面屈服以及受压翼缘与腹板屈曲. 构件屈曲时，与腹板交接处附近的受压翼缘以及腹板的中间部分均可能失效退出工作.

2）在构件达到极限弯矩Mu之前，翼缘宽厚比rf越大，屈曲越早，在受压翼缘上开展的塑性宽度越小，故极限弯矩Mu与边缘屈服弯矩Mec的比值越小. 构件在达到Mu之后，rw越大，因屈曲变形程度越大，截面失效范围越大，故Mu与Mec的比值越小，刚度退化越快. 轴压比n越大，Mu /Mec越大.

3）当板组相关屈曲系数δ<1时，截面几乎全部进入塑性，按全截面计算Mu，且考虑应力强化作用;当δ≥1时，按有效截面计算极限抗承载力Mu. 经与有限元计算结果比较，该方法能够准确计算各类冷弯薄壁矩形钢管柱极限抗弯承载力，并与GB 50018—2002《冷弯薄壁型钢结构技术规范》有效宽度法比较，发现规范设计计算较为保守.

参考文献

[1]    YU W W，LABOUBE R A.Cold-formed steel design[M]. Hoboken，NJ：John Wiley & Sons Inc，2010：1—26.

[2]    周绪红，王世纪.薄壁构件稳定理论及其应用[M]. 北京：科学出版社，2009：127—148.

ZHOU X H，WANG S J. Stability theory of thin-walled members and its application [M]. Beijing：Science Press，2009：127—148. （In Chinese）

[3]    彭雄，杨娜，王彬，等. 冷弯卷边槽钢轴压屈曲机理试验与数值研究[J]. 湖南大学学报（自然科学版），2013，40（8）：34—39.

PENG X，YANG N，WANG B，et al. Experimental research and simulation on lipped channel under axial compression [J]. Journal of Hunan University （Natural Sciences），2013，40（8）：34—39. （In Chinese）

[4]    邓长根，张晨辉，周江，等. H形截面压弯钢构件板组弹塑性相关屈曲分析[J].同济大学学报（自然科学版），2016，44（9）：1307—1315.

DENG C G，ZHANG C H，ZHOU J，et al. Plate assembly elasto-plastic interactive buckling analyses of H section steel members under compression and bending[J]. Journal of Tongji University （Natural Science），2016，44（9）：1307—1315. （In Chinese）

[5]    曾锋. 冷弯薄壁矩形钢管板组相关屈曲性能研究[D]. 西安：西安建筑科技大学，2003：13—57.

ZENG F. Local interactive buckling behavior of cold-formed rectangular tube [D]. Xian：Xian University of Architecture and Technology，2003：13—57. （In Chinese）

[6]    钢结构设计标准：GB 50017—2017[S]. 北京：中国建筑工业出版社，2017：14—15.

Standard for design of steel structure：GB 50017-2017[S]. Beijing：China Architecture & Building Press，2017：14—15. （In Chinese）

[7]    冷弯薄壁型钢结构技术规范：GB 50018—2002[S]. 北京：中国标准出版社，2002：30—33.

Technical code of cold-formed thin-wall steel structures：GB 50018—2002[S]. Beijing：Standards Press of China，2002：30—33. （In Chinese）

[8]    CHENG X，CHEN Y Y，PAN L L. Experimental study on steel beam-columns composed of slender H-sections under cyclic bending[J]. Journal of Constructional Steel Research，2013，88：279—288.

[9]    程欣，陈以一. 考虑板件相关作用的H形截面压弯钢构件抗弯承载力[J]. 工程力学，2015，32（3）：41—49.

CHENG X，CHEN Y Y. Moment resistance of H-section steel beam-columns considering the interactive effect of plate elements [J]. Engineering Mechanics，2015，32（3）：41—49. （In Chinese）

[10]  CHEN Y Y，WU X X，TIAN H，et al. Experiment on non-compact H-shaped members and frames subjected to cyclic loads and the prediction of capacities[J]. Steel Structures，2006（6）：215—226.

[11]  YANG N，ZHONG Y N，MENG Q T，et al. Hysteretic behaviors of cold-formed steel beam-columns with hollow rectangular section：Experimental and numerical simulations[J]. Thin-Walled Structures，2014，80：217—230.

[12]  YOUNG B，YAN J T. Finite element analysis and design of fixed-ended plain channel columns[J]. Finite Elements in Analysis and Design，2002，38（6）：549—566.

[13]  BANNO S，MAMAGHANI I H P，USAMI T，et al. Cyclic elastoplastic large deflection analysis of thin steel plates[J]. Journal of Engineering Mechanics，1998，124（4）：363—370.

[14]  周天華，李艳春，吴函恒，等. 冷弯薄壁型钢拼合箱形截面短柱承载力叠加法[J]. 湖南大学学报（自然科学版），2020，47（11）：46—55.

ZHOU T H，LI Y C，WU H H，et al. Superposition method for bearing capacity of cold-formed thin-walled steel built-up box section short columns[J]. Journal of Hunan University（Natural Sciences），2020，47（11）：46—55. （In Chinese）