基于方差-协方差法的VaR测算

肖成硕

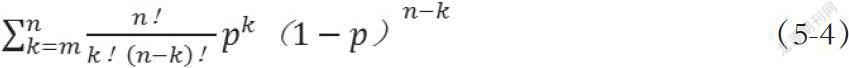
摘要：自J.P.摩根银行开发VaR方法以来，VaR这一风险管理工具在金融市场的风险管理中得到了广泛应用。本文选取笔者自选股中四只股票歌尔股份（002241）、华鑫股份（600621）、哈高科（600095）、福建水泥（600802）组成标的资产组合，并采用各股2018年6月19日到2020年6月15日的日对数收益率数据，在一定的假设条件下，采用方差-协方差法分别建立1-day99%VaR模型并进行测算，并对预测结果进行回溯测试，分析方差-协方差法测算VaR的优劣。

关键词：VaR;方差-协方差法;回溯测试

一、风险价值VaR以及测算方法

风险价值（Value at Risk，VaR）试图对金融机构的资产组合提供一个单一风险度量，而这一度量恰恰能体现资产组合的整体风险。该概念最早由J.P.Morgan公司公开发表。该方法传播开后很快得到了金融机构和学术界的认同。在市场正常波动条件下，当使用VaR来检测风险时，VaR是指在一定概率下，某一金融资产或金融资产组合的VaR是在未来特定一段时间T内的最大可能损失。其数学式表达为：

其中随机变量∆P为金融资产或金融资产组合在风险估计期间T内的价值变动量。

VaR的估算关键在于描述投资组合在评估期间收益的概率分布，常用的方法有：历史模拟法、协方差矩阵法和蒙特卡罗模拟法。本文使用方差-协方差法计算VaR。

方差-协方差法又称模型构建法，该方法基于马科维茨对于投资组合管理的理论，由资产组合中的标的资产的收益率均值和方差以及各资产之间的相关性，计算出投资组合的方差及协方差。假设组合中的各项资产的收益率变化均服从正态分布，并且假设资产组合价值的收益率变化也服从正态分布，由此根据公式prob（∆P>VaR）=1-X% 结合正态分布特性可以很容易的计算出组合的VaR。

二、 数据来源及描述

本文选取笔者A股股票账户自选股中四只股票歌尔股份（002241）、华鑫股份（600621）、哈高科（600095）、福建水泥（600802）组成资产组合。从CSMAR数据库中调取上述四只股票在2018年6月19日到2020年6月15日期间的一共1490份日收盘价数据作为本文所研究的基本样本数据

假定所持有的交易组合初始交易头寸的数量为400万元，每只股票的头寸均为100万元，即各股头寸权重相等。定义△xi为资产第i天的回报，投资αi数量与资产i所产生的的日回报为αi△xi，并且

公式中，αi，△P以百万计。

本文所计算的1-Day 99% VaR针对的是资产组合日收益率变动在置信度为99%下的风险价值，故本文所分析的样本数据设定资产组合的日回报为日对数收益率，其数学表达式为：

三、方差-协方差法计算VaR

（一）方差-协方差法

1.基本假设

对四只股票的对数收益率数据进行正态分布模拟可以发现，各股的实际分布与模拟的正态分布曲线并不相符，同时还存在着尖峰肥尾现象，但由于样本数据足够大，可以粗略的利用正态分布来近似处理计算VaR。因而方差-协方差法可用于计算VaR的一个重要假设为资产组合的收益率变化服从正态分布，并且交易组合价值每天的变化也服从正态分布，该假设同时还满足每日回报相互独立且具有相同的方差，则可以用日波动率σ2来表示。

同标准差相比，收益率的波动在一个较小区间内变化的期望值相对较小，为了方便计算，假定在展望期上个股i以及投资组合的期望收益率变动△P的期望值为0，并且假设收益率是一个平稳的时间序列。

2.基本原理

在设定上述假设的情况下，方差-协方差法计算VaR对由股票组成的资产组合十分适用，其基础是马科维茨关于投资组合管理的先驱性理论，由资产组合中的标的资产的收益率变动均值和方差，以及资产回报之间的相关性，可以计算出投资组合收益率变动的方差及协方差矩阵，再根据正态分布的特性，在预设的置信度下算出分位数，根据公式（2-1）可以计算出一定展望期下的VaR，其VaR值随时间长度的平方根增长。则VaR的数学表达式为：

其中z值为预设置信度X%下对应的临界值;T为展望期;σp为组合价值日变动标准差

（二）计算过程

第一步，计算投资组合的日收益变动ΔP的标准差σp。

假定σi为第i项资产的日波动率，ρij，为资产i及资产j的相关系数，则Δxi的标准差σi将ΔP的方差记为σ2p，则σ2p的数学表达式为：

设定置信度X为99%，展望期T=1天，根据公式（3-1）则持有的交易组合的价值为P，在交易组合中有4个不同资产，投资组合中资产i（1≤i≤4））的数量为αi，则αi均等于1百万元，对相关系数和波动率进行计算，可使用方差和协方差，变量i的每日变化的方差vari等于每日变化波动率的平方，变量i和j的协方差等于i和j每日波动率、相关系数ρij，三项乘积。

则式（5-2）中投资组合ΔP的方差可以表达为：

根据第三章中的历史收益率数据对所有数据设定等同权重，运用EXCEL的数据分析功能计算出资产i和j的日对数收益率的相关性矩阵和协方差矩阵，如下表所示：

由公式（5-3）计算得投资组合的价值变动ΔP方差σ2p=0.008320163，则交易组合收益率变动的标准差σp=0.091214927。

第二步，计算VaR。

由VaR计算公式（5-1）计算得1-day 99%VaR=2.33*0.09121=0.212（百万）得出交易组合在99%的置信度下1天展望期的VaR为21.2萬元。

（三）回溯测试

根据方差-协方差法测算出标的组合的VaR后，对VaR进行回顾测试，检验该方差-协方差模型的表现，如果1-day99%VaR的方差-协方差模型准确无误，那么每天的损失超出VaR=21.2万元的概率p=1%，每天的损失是否超过VaR服从二项分布的性质，建立两种对立假设：

根据组合加权平均日收益时序图，可以发现在484个观察日中出现7天的损失超出了根据模型测算的VaR，选定5%的置信度，通过Excel中BINOMDIST函数计算在484次独立实验中有7天或更多天实际损失超出VaR的概率。通过计算对应7次或者更多的例外发生的概率为1-BINOMDIST（6，484，0.01，TURE），计算数值为0.214，说明7次或者更多的例外发生的概率大于5%，不拒绝假设1。

四、总结

方差-协方差法总是假定收益率服从一定的分布，如前文就假定了收益率服从正态分布，这样计算相对简便，结果也很直观明了，但这种假设收益率分布所得出的结果是否有效很大程度上依赖于收益率分布假设的正确与否，倘若假设的分布不正确，产生的误差就很大。然而正如前文中对标的资产收益率的分布图所示，时间序列一般来说并不满足正态分布，故用该方法计算出的VaR值可能不够准确。而后续的回溯测试也证明，事实已经证明，收益率的分布是厚尾的，因而正态性的假定会导致对极端事件 VaR 的低估。

参考文献：

[1]（加）赫尔著.风险管理与金融机构[M].原书第三版.北京：机械工业出版社，2013.04

[2]贾馨云，苏应生，高春燕.VaR模型在股市风险分析中的应用及实证分析[J].中国管理科学，2014，22（S1）：336-341.

[3]周革平.VaR基本原理、计算方法及其在金融风险管理中的应用[J].金融与经济，2009（02）：69-71+78.