十字梁六维力传感器应变组桥方式对维间串扰的影响



摘要:在载荷作用下六维力傳感器不同方向输出存在互相干扰,如何降低串扰是多维力传感器技术中面临的主要问题。惠斯通电桥法是其中手段之一,是当前应变式传感器信号采集的主要方式。但六维力传感器包含的应变片数量较多,电桥电路不止一种组建方式,组桥形式对维间串扰精度的影响决定了传感器精度设计时的硬件选择和成本控制。为避免工艺、实测偏差等因素影响,本文主要通过对十字梁六维力传感器不同组桥形式下的仿真参数计算对比,分析应变组桥方式对维间串扰的影响。
关键词:六维力传感器;维间串扰;差动全桥
0 引言
应变式力传感器的工作原理是在力作用下弹性体表面产生应变,引起粘贴的应变片阻值变化,通过惠斯通电桥将机械信号转化为电信号[1],再经过标定等运算处理后得到加载力值大小。六维力传感器是一种可以检测空间坐标系下X方向力和绕X坐标轴的扭矩、Y方向力和绕Y坐标轴的扭矩、Z方向力和绕Z坐标轴的扭矩这六个维度的力参数的力传感器[2],随着测力维度数量的增加,各个参量之间的相互影响也越来越大,该影响程度称为维间串扰(耦合),如X、Y向的力对Z向的扭矩的串扰。
串扰的产生的根本原因是在检测非主方向力的应变片上检测到了应变的存在,从而通过电桥产生了输出[3]。串扰应变的产生是弹性材料结构上的固有性质,串扰较大时很难通过算法解耦。应变串扰虽然无法完全消除,但由于十字梁传感器结构对称,串扰应变常常是成对出现且大小相等,可以通过改变应变电桥组桥形式来减小非主方向的电桥电压输出。
1 电桥输出与应力关系
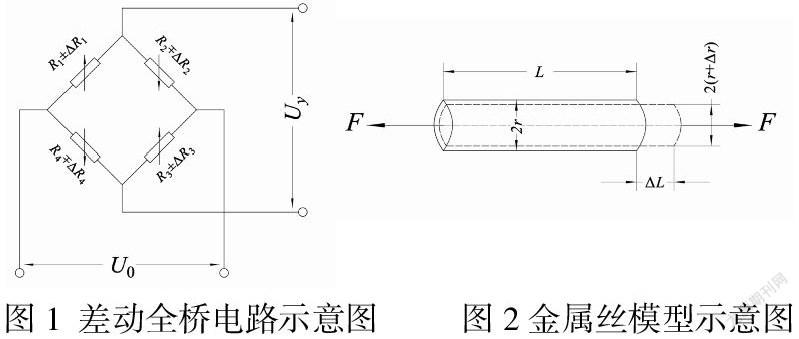
六维力传感器组成桥路的应变片一般为四个,分布在弹性梁相对对称的位置组成差动全桥电路。在检测到力的存在时,一个桥路有两对应变片的输出应变大小相等方向相反且每对中的两个应变片的输出等大同向,分布在不同半桥的相对位置(如图1所示的R1和R3、R2和R4位置),桥路中相邻的应变片检测应变方向相反。
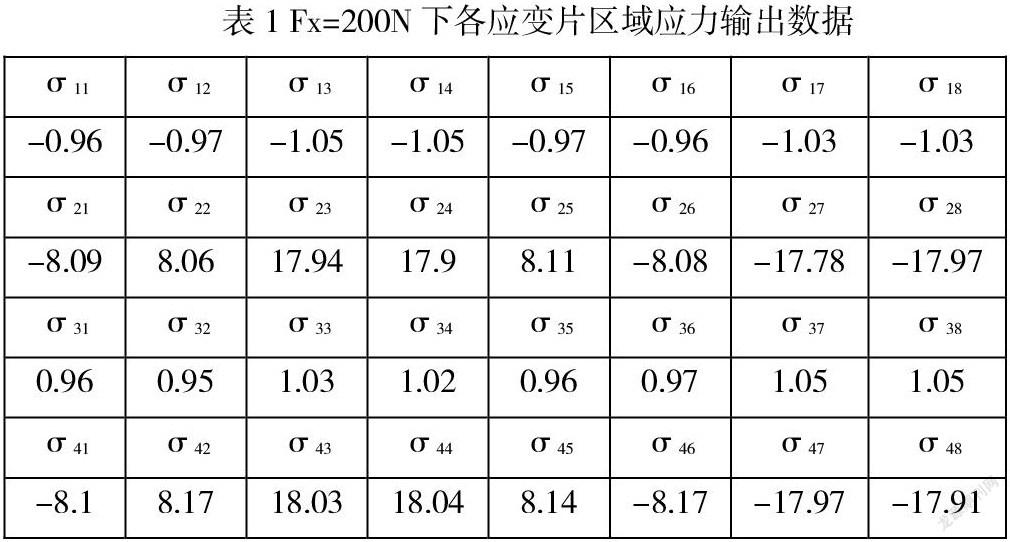
金属箔式应变片是将金属丝经高温液化后高压高速喷射,雾化沉积在基片上形成3~10μm层,再用光刻腐蚀法形成电路。其优点是:横向效应小,允许电流大,柔性好、蠕变小、疲劳寿命长,生产效率高。金属丝在外界力的作用下产生机械变形时,其电阻值相应发生变化。如图2所示其电阻变化率为
其中K称为单根金属丝的灵敏度,即单位应变的电阻变化率。ρ电阻率;ε 应变;μ泊松比;λ压阻系数;E弹性模量
电桥电压的输出大小由应变片电阻变化量决定,而应变片电阻变化是弹性体应变引起的,因此可以得出电桥最大输出电压与应变的关系:
式中输入电压U0为常数,应变片灵敏度系数k也为常数,则输出电压与应变成常系数线性关系。因此直接将仿真应变按电桥输出电压计算可以准确反映传感器的输出特性。在仿真中,应变与应力关系为,弹性模量E与材料相关为一常数,故可以进一步排除材料因素影响,通过应力分析也能准确评估传感器输出特性。即
2 传感器模型建立及仿真计算
2.1六向应力计算方法
六维力传感器涉及六个主方向参量,根据前文分析可知,传感器主方向应力与电桥电压呈正比关系σ∝U,而由材料力学可知F∝σ,则F∝U:
式中C为系数矩阵。
图3所示一种常见的十字梁六维力传感器弹性体,共有四根短横梁,应变片粘贴在弹性梁靠传感器中心的位置,每根梁粘贴8个应变片,每四个应变片可以组成一路全桥电桥。根据全桥最大电压原理,可以形成单梁自组桥形式(如图4a)、相对梁单侧组桥形式(如图4b)和相对梁对侧组桥形式(如图4c)。根据应力与电桥电压输出特性,各方向应力为:
式中n表示参与主应力方向的应变片数量,i表示参与主应力方向的弹性梁数量,j表示这些弹性梁上参与主应力方向的应变片位置。以双梁对侧组桥示例:
2.2仿真结果分析
仿真模型参数如下:
应变片检测的是弹性体表面应变,方向为栅丝长度方向,但实际上弹性梁在受力时表面为二向应力状态,垂直主应变方向也存在应变量,故在仿真中需要指定应力方向,设置沿弹性梁长度方向求解方向应变(normal stress)表征应变片实际工作状态。为保证参数一致性,应力仿真区域应设置为应变片粘贴区域,选取的区域尺寸应绝对对称和相等。同时加载力应作用于弹性体形心位置,避免引入偏置载荷。使用ANSYS Workbench仿真结果如下(篇幅有限仅以Fx加载应力示例,下同):
II类误差值是评价六维力传感器解耦算法优劣性的重要指标,反映了该方向未施加力/力矩时,他其方向施加的力/力矩值对该方向信号产生的干扰[4]。
其中,yi(F.S)表示i方向可施加力/力矩的满量程值,ysi(max)表示当s(s=j,k,l,m,n)方向施加力/力矩值,其他方向无作用力/力矩时,i方向测得的最大值。则各桥路应力及串扰误差分别计算的结果如下:
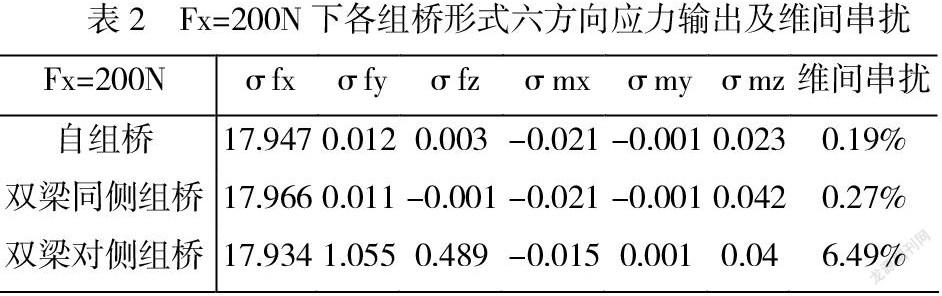
由表1可以看出,当力Fx作用时,虽然σ23为主方向应力17.9Mpa,但在决定Mx向的σ21上同时输出了-8Mpa的应力值,这反映了弯曲正应力对切应力的影响。应力桥路会将这种耦合影响同时输出,如果应力变化同向且位于同桥臂,如双梁对侧桥路,那么桥路输出占比就会变大,串扰误差就会增大。
但在表2中Fx作用下σmx的值却非常小,说明在Fx作用时,组成Mx测力输出的桥路,两个变化方向相同(相反)的应变片刚好分布在相同(不同)桥臂上,使桥路输出几乎为零,从而整体表现为仅存在主方向Fx的输出,这就形成了一种硬件解耦的方式。
由表格结果来看,单梁桥路的维间串扰低于双梁桥路,表现为传感器整体的精度较高。因此在十字梁六维力传感器设计时,优先选用单梁自组桥方式,具有更高的设计精度。
3 结论
本文通过对十字梁型六维力传感器的应力仿真参数进行分析计算,得出了传感器单梁组桥的串扰误差比双梁组桥更小的结论,并且基于应力原始数据对单梁组桥优异性机理进行了分析,为后续六维力传感器的桥式电路设计和选择提供借鉴。
本文仅对电桥形式产生的串扰结果进行了比对判断,但原始应力串扰的产生原因仍是需要进一步研究的内容,通过仿真结果和弹性体结构可以初步判断,弹性梁的支承结构及尺寸是应力串扰产生的关键影响因素。如果最原始的应力串扰输出可以大幅削减,那么这种多维力传感器使用精度将大幅提高,对航空航天风洞试验测试、船舶潜艇容压检测等具有重要意义。
参考文献
[1]Perry D. Multi-Axis Force and Torque Sensing[J]. Sens Rev,1997,17: 117 - 120.
[2]肖汶斌,董文才. 六维力传感器静态解耦算法[N]. 武汉: 海军 工程大学学报,2012.
[3]Ma Junqing,Song Aiguo,Xiao Jing. A Robust Static Decoupling Algorithm for 3-Axis Force Sensors Based on Coupling Error Model and ε-SVR[J]. MDPI. Basel,Switzerland. October,2012,12 ( 11) : 14537 - 14555.
[4]徐科军,李成.多维力传感器静态解耦的研宄[J].合肥工业大学学报(自然科学版),1999,(02):3-8.
作者简介:王拓1994年11月;性别:男;民族:汉;籍贯:河南省南阳市;职务职称:格力电器装备动力技术研究院专业研究组组长/助理工程师;学历:本科;单位:珠海格力电器股份有限公司;研究方向:传感器及智能装备

