基于Matlab的过盈计算


摘要:在传统过盈计算的基础上,引入Matlab软件,利用Matlab强大的计算能力,以及Simulink可视化、模块化操作界面,针对过盈配合中复杂的结构件的配合计算提出新方法。在此过程中结合制图常用的CAD软件,实现模型(CAD)、平台(Simulink)、计算(Matlab)之间的联合仿真,以实现设计-计算的快速迭代,减轻初步方案设计中校核的工作量。在轴-齿轮过盈配合计算中,使用Matlab仿真计算得出的结果与有限元仿真计算结果趋于一致。另外,试验以及后续实际使用验证了这种结果的可靠性和准确性。
Abstract: On the basis of traditional interference calculation, Matlab software is introduced, Matlab's powerful computing power, and Simulink visualization and modular operation interface are used to propose a new method for the matching calculation of complex structural parts in interference fit. In this process, the CAD software commonly used in drawing is combined to realize the joint simulation between the model (CAD), the platform (Simulink), and the calculation (Matlab) to realize the rapid iteration of design-calculation , reduce the workload of verification in the preliminary scheme design. In the calculation of the shaft-gear interference fit, the results obtained by using Matlab simulation calculation and the finite element simulation calculation results tend to be consistent. In addition, the test and subsequent actual use have verified the reliability and accuracy of this result.
关键词:过盈计算;Matlab;Simulink;有限元;应力
Key words: interference calculation;Matlab;Simulink;finite element;stress
中图分类号:TP391.9 文獻标识码:A 文章编号:1674-957X(2021)10-0001-04
0 引言
在传动系统中,轴-套类零件过盈配合的稳定性是保证整个系统可靠的重要一环,尤其是对采用过盈连接的齿轮传动系统来说其更为重要[1]。在每次设计中,轴-齿轮的过盈计算均是必不可少的一环。目前已有的经典计算方法准确度不高,且无法面对复杂结构的过盈配合计算,比如齿轮的轮辐结构;而基于Ansys的有限元计算方法,其前处理又太过复杂,并且针对后期模型的改动,需要做大量的重复性工作[2][3]。这些已有的计算方法无法很方便高效的解决过盈连接设计工作中的问题,因此本文提出基于Matlab的过盈计算方法,以解决传统计算方法面对复杂的连接结构,无法准确并快速的给出过盈量与传递扭矩之间的关系以及过盈中包容件与被包容件应力分布情况的问题。基于Matlab的过盈计算方法,在大大降低工作量的同时,提高计算的准确度[4]。在机械传动中,需要靠稳定的连接结构来保证传动的可靠性,而过盈连接因其结构简单、定心性强、受冲击影响小、对轴的强度几乎无削弱等优点而被广泛采用。特别是在轨道车轴上更是如此。过盈连接主要是通过过盈产生的挤压力使结合面紧密贴合,从而产生足够的摩擦力以传动扭矩和轴向力[5]。
本文以某高铁齿轮箱车轴与齿轮的过盈配合为例,运用Matlab仿真软件Simulink模块,在计算过程中直接从CAD图纸中提取模型信息,进行联合仿真计算,并以基于Ansys的有限元软件进行验证。
1 过盈理论计算
1.1 经典力学模型
在齿轮与车轴的过盈配合中,车轴作为动力输出,与齿轮(动力输入)之间仅靠过盈产生的摩擦阻力矩传递扭矩。根据弹性力学理论,将轴和齿轮之间的压力看作沿结合面均匀分布的均布力,并且将材料看作是均匀理想的弹塑性材料,其受力分析如图1所示,图中左侧为轴受力模型,右侧为轴套(齿轮)受力模型。
1.2 受力分析计算
根据上述力学模型进行分析计算,假设结合面的过盈量为e,则结合面的压力pf为:
式中:e——结合面的过盈量(mm);
df——结合面的直径(mm);
da——包容件外径(mm);
di——被包容件内径(mm);
Ca、Ci——包容件、被包容件传递载荷所需的最小直径变化量;
Ea、Ei——包容件、被包容件材料的弹性模量(MPa);
νa、νi——包容件、被包容件材料的泊松比;
qa、qi——包容件、被包容件的直径比。
在车轴过盈计算中,齿轮为斜齿轮,受到扭矩T与轴向力Fx的共同作用,故齿轮在扭矩与轴向力的作用下不产生滑移的最大扭矩T与结合面的压力pf之间的关系如下:
式中:Ft——传递力(N);Fx——轴向力(N);K——安全系数;lf——配合面长度(mm);μ——配合面摩擦系数。
由结合面的压力pf可计算出包容件和被包容件所受到的应力。
式中:σa、σi——包容件、被包容件受到的应力(MPa)。
2 Matlab仿真计算
2.1 Simulink仿真建模
利用上述经典受力分析所建立的力学模型编制仿真程序,并由CAD导入模型,构建齿轮和轴的离散化轮廓模型,用Matlab建立结合面的直径df、包容件外径da、被包容件内径di等随着结合位置变化的离散化函数关系。本文给出计算的主要过程,提供选择过盈量的过盈-扭矩曲线,并根据选择的配合公差得到最大过盈量,以此来计算面压力和绘制包容件、被包容件的应力分布曲线。
在Matlab中的Simulink模块中建立可视化仿真单元(如图2所示),其中主程序为计算的核心程序,内部采用上述的经典受力分析。图2中左上角的“几何参数”是CAD导出的轮廓模型经过函数的转化而形成的可供Matlab直接读取使用的曲线函数。过盈量e在計算中可有多种选择,在第一种模式下e是一次函数变化曲线,由此可以计算绘制出过盈量-扭矩曲线,这为最小过盈量的选择提供理论计算依据。后两者为校核模式,在选出配合与公差后使用,可计算出包容件、被包容件的应力,校核结合件是否发生塑性变形。本文拟将主程序写出以供参考。
图2以某高铁齿轮箱齿轮与轴的数据为输入条件,其中电机短路时齿轮受到的扭矩为36820N.m,在齿轮中产生的轴向力为40130N,摩擦系数为0.14。
2.2 Matlab主程序
使用matlab函数创建主程序,如下所示:
function T = quxian(quxian11, quxian12, quxian21,
quxian22, e, u, Ea, Ei, va, vi, Fx)
[~, m11] = size(quxian11);
% quxian11为被包容件内轮廓离散曲线,并计算数据的大小。
[x11, ~] = min(quxian11, [], 2);
% 查找数据的起始位置。
[~, m12] = size(quxian12);
% quxian12为被包容件外轮廓离散曲线,并计算数据的大小。
[x12,~]=min(quxian12, [], 2); [~, m21]=size(quxian21);
% quxian21为包容件内轮廓离散曲线,并计算数据的大小。
[x21, ~]=min(quxian21, [], 2); [~,m22]=size(quxian22);
% quxian22为包容件外轮廓离散曲线,并计算数据的大小。
[x22,~]=min(quxian22, [], 2); xmin=[x11,x12,x21,x22];
%查找四条曲线数据的起始位置。
x0 = max(xmin, [], 2); x0max=x0(1, 1);
%提取起始点横坐标。
xmax = [m11, m12, m21, m22]; x1min = min(xmax);
%提取四条轮廓曲线中最短曲线终止点的横坐标。
xmax = [m11, m12, m21, m22]; x1max = max(xmax);
%提取四条轮廓曲线中最长曲线终止点的横坐标。
shuzu0 = zeros(2, x11(1, 1)*10);
shuzu1 = zeros(2, x1max-x11(1, 1)*10-m11);
quxian11 = cat(2, shuzu0, quxian11, shuzu1);
shuzu0 = zeros(2, x12(1, 1)*10);
shuzu1 = zeros(2, x1max-x12(1, 1)*10-m12);
quxian12 = cat(2, shuzu0, quxian12, shuzu1);
shuzu0 = zeros(2, x21(1, 1)*10);
shuzu1 = zeros(2, x1max-x21(1, 1)*10-m21);
quxian21 = cat(2, shuzu0, quxian21, shuzu1);
shuzu0 = zeros(2, x22(1, 1)*10);
shuzu1 = zeros(2, x1max-x22(1, 1)*10-m22);
quxian22 = cat(2, shuzu0, quxian22, shuzu1);
%以上为统一曲线的起始和终止点位置,并统一数据矩阵的长度。
xx = quxian11(1, :);
jisuan11 = 2*quxian11(2, :); %被包容件内径。
jisuan12 = 2*quxian12(2, :); %被包容件外径。
jisuan21 = 2*quxian21(2, :); %包容件内径。
jisuan22 = 2*quxian22(2, :); %包容件外径。
% 以下为过盈计算。
qa = jisuan21./(jisuan22+eps); %包容件直径比。
qi = jisuan11./jisuan12; %被包容件直径比。
Ca = (1+qa.*qa)./(1-qa.*qa)+va; %包容件刚性。
Ci = (1+qi.*qi)./(1-qi.*qi)+vi; %被包容件剛性。
pf = e/jisuan12./(Ca/Ea+Ci/Ei); %结合面压力。
ea = pf.*jisuan21.*Ca/Ea;
%包容件结合面直径变化量。
ei = pf.*jisuan12.*Ci/Ei;
%被包容件结合面直径变化量。
FT = 0; DF = 0;
%以下为计算结合面压力随结合位置的函数关系,以及扭矩T和过盈量e的函数关系。
for i = x0max*10+1:x1min+x0max*10
if jisuan21(1, i)-jisuan12(1, i) < 0.1
Ft = (0.1*pi*u*pf(1, i)*jisuan12(1, i));
DF = DF+jisuan12(1, i);
else
pf(1, i) = 0; Ft = 0;
end
FT = Ft+FT;
end
for i = 1:x0max*10
pf(1, i) = 0;
end
for i = x1min+x0max*10:x1max
pf(1, i) = 0;
end
df = DF/x1min;
T = sqrt(FT^2-Fx^2)*df/2000; %扭矩输出。
a = (1-qa.^2)./((3+qa.^4).^0.5); c = (1-qi.^2)/2;
Qsa = pf./a;Qsi = pf./c;
plot(xx, Qsa', '-');
%包容件应力随结合点位置变化的曲线关系。
hold on
plot(xx, Qsi', '-');
%被包容件应力随结合点位置变化的曲线关系。
end
2.3 仿真结果
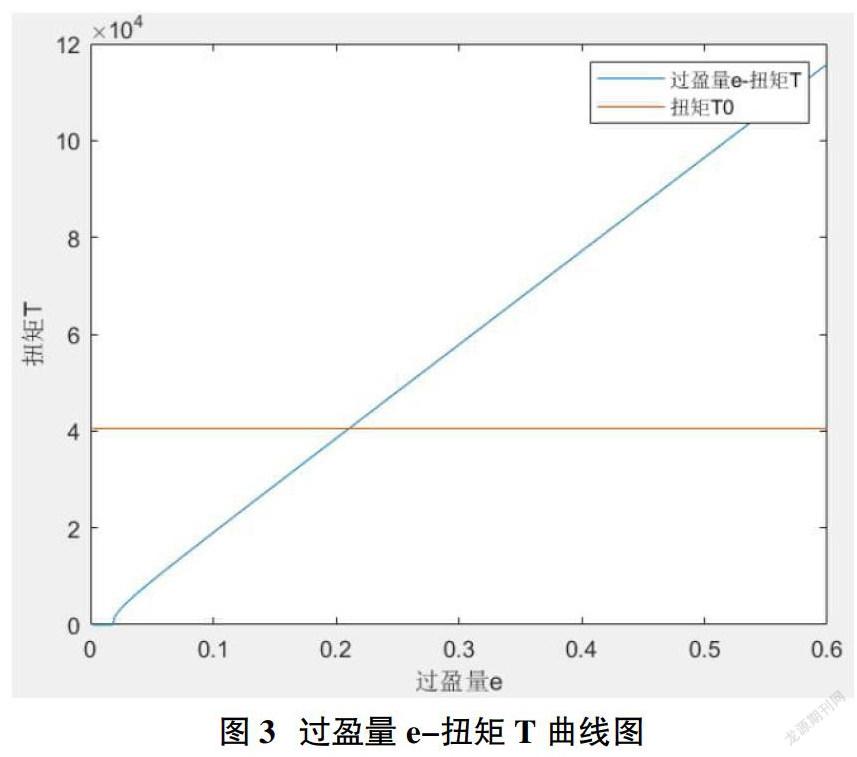
上述程序运行后,通过控制不同的输入和输出,可以得到图3过盈量e-扭矩T曲线图(图中蓝色斜线)。安全系数取1.1,用需要达到的目标扭矩T0绘制一条横线(图中红色横线),此横线与过盈量e-扭矩T曲线相交点即为最小过盈量,经计算最小过盈量为0.211mm。
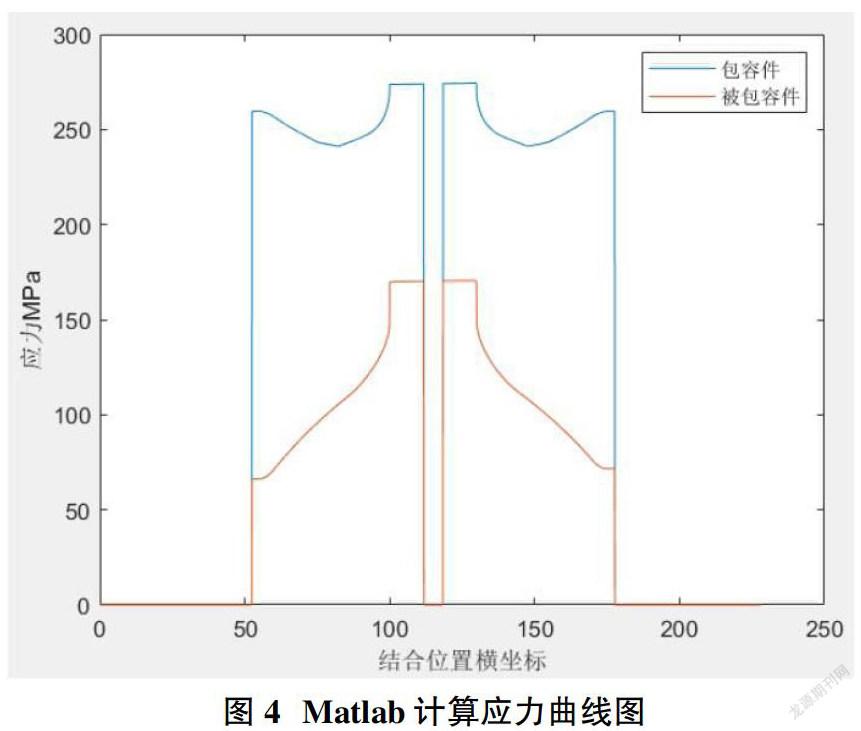
根据最小过盈量以及公差配合表,查表计算得到最大过盈量为0.287mm。修改输入条件,计算在最大过盈量下包容件和被包容件的应力,计算结果如图4所示,蓝色为包容件的结合面面压力,红色曲线为被包容件的结合面面压力。
3 有限元计算结果验证校核
3.1 有限元仿真设置
本文的Matlab方法需要经过更为详细的有限元计算进行校核。利用有限元软件对轴和齿轮的过盈配合进行仿真,并与使用Matlab软件计算出的轴和齿轮的应力结果进行对比,以校核Matlab方法的可行性、准确性。
为了使有限元与Matlab的计算模型保持一致,并降低计算机的计算量,对模型进行简化处理,如下所示:
①去除模型中修饰性倒角、倒圆以及对网格质量影响较大的孔结构;
②去除多余无效部分,保留计算中需要的关键模型;
③对齿轮轮齿部分作简化处理。
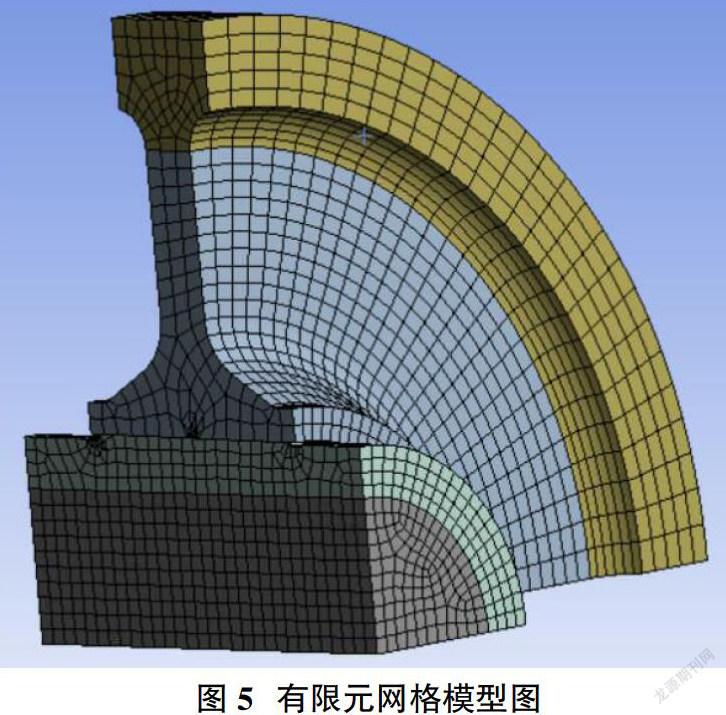
如图5所示,采用六面体网格结构对模型进行网格划分,共计39896个单元、181143个节点。
边界条件:
在齿轮外圈设置固定约束,给结合面施加最大过盈约束,摩擦系数选取0.14。
3.2 仿真结果以及对比
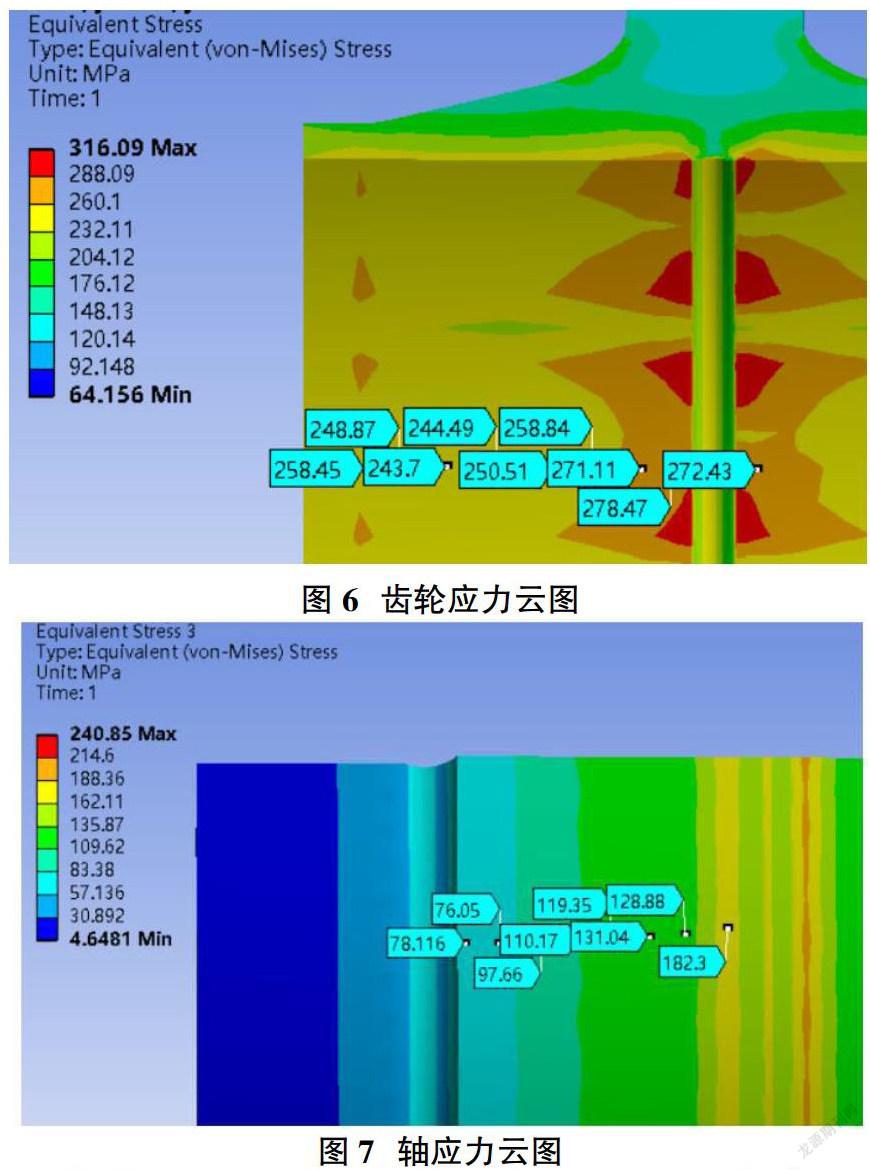
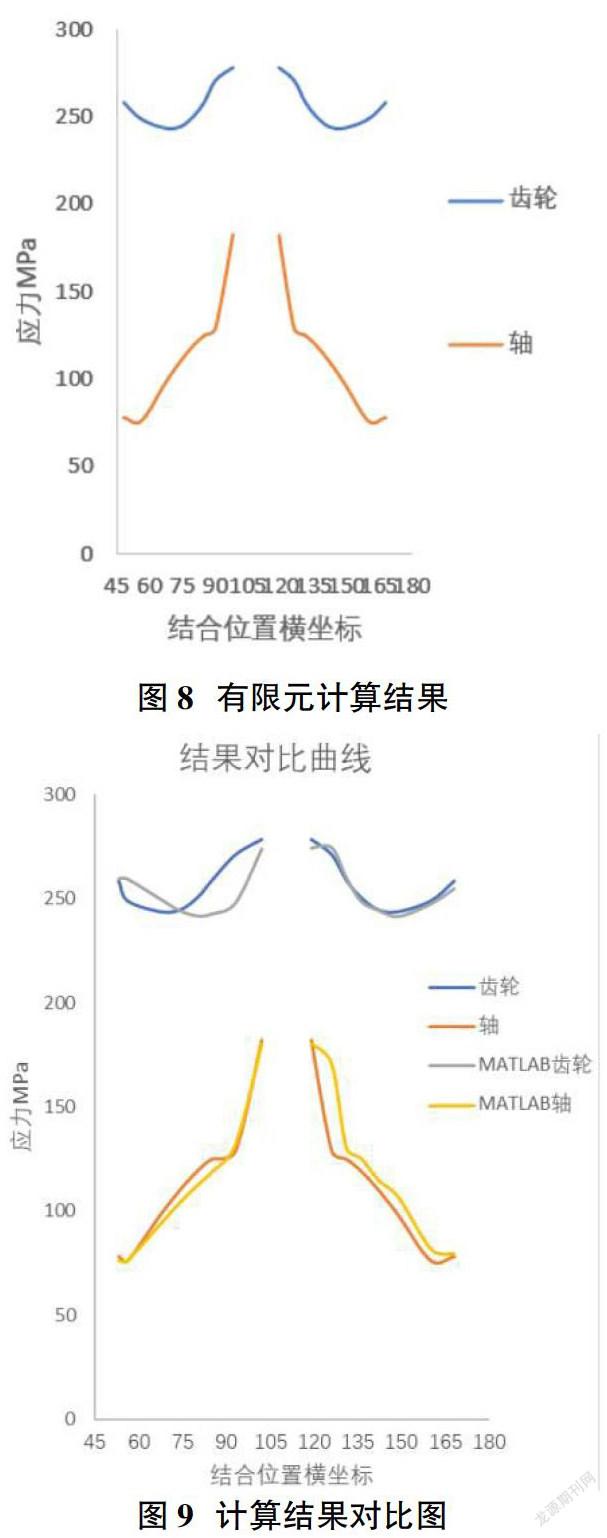
仿真运算后,选取特征点,并绘制轴上应力-结合位置曲线(如图6、图7、图8所示)。因为左右两侧对称,故只显示左侧计算结果。有限元仿真结果与Matlab仿真结果对比(如图9所示),其变化趋势一致,并且数值上非常接近,同理再次对比齿轮上有限元与Matlab应力-结合位置曲线,二者变化趋势一致,数值接近。经计算峰值误差率约为8.5%,远低于±20%,误差率的均方差不足4%,低于5%。峰值误差出现在变化曲率较大的区域,考虑到有限元结果为手工选点,存在人为的误差,以及直径突变处,存在仿真与实际不符的情况,对比结果符合预期,证明该方法针对复杂形状的包容件、被包容件具有快速、误差低、计算结果可靠等优势。
本论文引用的高铁齿轮箱已投入使用,在加载试验以及线路运行过程中使用情况良好,并且运营考核完成后的大修拆解中,未发现齿轮滑移、过盈部位塑性变形等失效情况。
4 结论
本文以某高铁齿轮箱为例,针对复杂结构建立了基于Matlab的过盈计算新方法,并结合工程设计中常用的CAD软件,实现模型-平台-计算联合仿真。运用成熟可靠的有限元软件对该方法进行校核,并把两者之间的结果对比,得到了比较满意的结果。在后续的使用中,可以随时调整输入参数。模型更改后只需要做简单的导出,导出结果无需经过特殊处理,即可直接运用于Matlab的计算,类似傻瓜式操作,在确保准确性的同时又提升了迭代速度。该方法给机械设计提出了新的方式方法,在实际的工程应用中充分证明了该方法的适用性以及广泛性。Matlab软件以其强大的计算能力在联合仿真以及工程设计中起到了巨大的作用。
参考文献:
[1]高旺,付赟秋,张辙远.高铁车轴与齿轮过盈配合计算与分析[J].内燃机与配件,2019(03):54-56.
[2]李伟建,潘存云.圆柱面过盈连接的应力分析[J].机械科学与技术,2008(03):313-317.
[3]李亚洲,汤易升,陈炜,张西正.基于ANSYS Workbench对圆柱面过盈配合接触应力的研究[J].天津理工大学学报,2017,33(03):1-5.
[4]程林章,王洪军.MATLAB在轴类零件过盈配合中的仿真应用[J].机械研究与应用,2004(02):59-60.
[5]王少江,李学明,张安鹏,侯力.大型焊接齿轮与轴过盈配合有限元分析[J].煤矿机械,2015,36(05):134-136.

