基于多目标决策的多车场车辆调度干扰管理研究

曹庆奎 高亚伟 任向阳 袁雯慧

【摘   要】   针对客户配送地址产生变动而导致初始运输方案难以顺利实施这一难题，考虑客户、物流运营商和配送人员三个行为主体的利益，以客户不满意度、运输费用和路线偏离最小为目标，建立多车场环境下多目标干扰管理数学模型。对目标函数进行规范化处理，将多目标问题化简为单目标问题。对遗传算法进行改进，引入迭代交换过程和自适应交叉变异算子求解干扰管理模型。通过MATLAB软件进行仿真，仿真结果与重调度法进行对比。结果表明，文中本文方法与现有的重调度法相比可以更好地平衡各方利益，得出扰动较小的调整方案。

【关键词】   多目标;多车场;干扰管理;遗传算法

Research on disruption management of multi-depot vehicle scheduling based on multi-objective decision

CAO Qing-kui1，2， GAO Ya-wei1， REN Xiang-yang1， YUAN Wen-hui1

（1. Hebei University of Engineering， Hebei Handan 056038， China;2. Langfang Normal University， Hebei Langfang 065000， China）

[Abstract]  The initial distribution plan is difficult to implement due to changes in the customer distribution address. Aiming at this difficulty， this paper considers the interests of three actors： customers， logistics operators and distribution personnel， aiming at customer dissatisfaction， transportation cost and path deviation minimization， a multi-objective disruption management model in a multi-depot environment is constructed. Normalize the objective function and transform the multi-objective problem into a single objective problem. To solve the disruption management model， the genetic algorithm is improved by introducing iterated swap procedure and adaptive crossover mutation operator. Simulation by MATLAB software， the simulation results are compared with the rescheduling method. The results show that， compared with the existing rescheduling method， the method in this paper can balance the interests of all parties better and obtain a less disturbing adjustment scheme.

[Key words]  multi-objective; multi-depot; disruption management; genetic algorithm

〔中圖分类号〕  TP 301             〔文献标识码〕  A              〔文章编号〕 1674 - 3229（2021）01- 0000 - 00

0     引言

随着客户需求量的增多、客户网点分布不规则、企业规模不断扩大，单个配送中心往往无法满足配送需求，因此多车场车辆调度问题亟待解决。多车场车辆调度问题是基本车辆调度问题的扩展，是更为复杂的NP难题，近年来受到了国内外众多学者的广泛关注。Zhou等[1]探讨了带有燃料限制的多车场车辆调度问题，以总成本最低为目标，提出了四种新的混合整数线性规划公式来计算模型的最优解。Nadjafi等[2]探讨了带时间窗约束和车辆限制的多车场车辆调度问题，以最小配送费用为目标进行规划，设计出一种启发式算法，并成功的运用到180个实验案例中。颜瑞等[3]考虑了带有时间窗约束的多车场二维装箱车辆调度问题，构建数学模型，并提出由量子粒子群和局部搜索算法相结合的混合算法来求解。

多车场车辆调度问题在考虑运输成本的同时也要考虑客户满意度、使用的车辆数、运输时间等方面。所以，多车场车辆调度问题是典型的多目标组合优化问题，存在多个彼此冲突的目标。Mirabi等[4]以配送成本和客户等待时间最少为目标构建车辆调度模型，并采用混合电磁算法求解。Yoshinori等[5]以能耗和碳排放量最小为目标，构建带时间窗限制的多车场车辆调度模型，并设计了一种启发式算法求解。毕志升[6]等从物流运营商和客户方面考虑，研究了高维多车场车辆调度问题，并采用改进的遗传算法和进化算法对多目标模型进行求解。

在車辆运输的过程中，经常会发生一些干扰事件，如客户时间窗变动、车辆运力受扰、客户配送地址变动等，这些干扰事件的出现往往会对初始配送方案造成影响。因此，如何尽可能的小范围调整初始配送路线以达到扰动最小，是目前学术界关注的热点问题。王旭平[7]等探讨了车辆损坏状况下的多车场车辆调度问题，构建了干扰管理数学模型，采用了改进的遗传算法进行求解。王征[8]等考虑了顾客时间窗变动的干扰情况，以整体扰动最小为目标构建多车场车辆调度干扰管理模型，并设计了基于特定领域结构的变邻域搜索算法。郑丹阳等[9]研究了动态需求下的多车场车辆调度问题，设计了一种自适应量子蚁群算法，并验证了算法的可行性。

以上学者对多目标、干扰管理理论在多车场车辆调度领域的应用进行了深刻的研究。但是，有关客户配送地址变化的多车场车辆调度问题的研究甚少，并且现有的研究过分看重对物流运输成本的优化，往往忽视了人的行为因素。本文基于已有的研究，探讨了客户配送地址变化情况下的多车场车辆调度问题。考虑了客户，物流服务商和配送人员三者的利益，基于干扰管理思想构建出对应的多目标干扰管理数学模型，并将多目标问题转化为单目标问题，提出了针对该问题的简化解决方案。最后，采用改进的遗传算法求解数学模型，并检验了本文算法的可行性与有效性。

1     问题的描述及模型的建立

以车场和客户点间的配送网络为研究对象，假设物流服务商有[M]个车场，每个车场配备容量为[Q]的货车[Km （m=1， 2， ...， M）]辆，货车给[N]个客户实施物流配送服务，客户点[i]的需求量为[qi][（i=1， 2 ，...， N）]，车辆从各自的原始车场发车送货，在给客户配送完货物后返回初始车场。所有客户都能被任何一个车场的车辆服务，但每个客户仅仅可以被一辆车服务一次，且需求一次得到满足。设客户编码为[1， 2， ...， N]，车场编码为[N+1，N+2， ...， N+M]。

当物流配送计划执行到[t]时刻时，有客户的配送地址发生改变，使得原配送方案受到干扰，并且车场没有多余的送货车辆，没有完成的送货任务需依靠在途车辆继续配送。已知客户的期望时间窗，客户收到货物的时间不可早于客户能接受的最早服务时间，也不可晚于客户能接受的最晚服务时间。当出现干扰事件时，把在途车辆的位置当作初始位置，原车场当作终点。本文以客户配送地址变动作为干扰事件，所以当出现干扰时，没有完成送货任务的客户点集合也会产生变动，这需要两个客户点集合来加以区分。

1.1   问题假设

为了简化模型的构建与求解，让模型在现实中有更高的实用价值，对构造的模型给出如下假设：

（1）所有车场的坐标位置、配备货车的数量以及货车的最大运输量己知，且每辆车的型号相同;

（2）所有的运输车辆在初始车场发车，且完成送货后回到原车场;

（3）车场可利用的车辆数不可多于该车场配备的车辆总数;

（4）每辆车运输的重量不可多于该车的最大承重量;

（5）客户收到货物的时间不可早于客户能接受的最早服务时间，也不可晚于客户能接受的最晚服务时间;

（6）每辆车匀速行驶，且速度已知;

（7）每辆车的单位行驶成本固定;

（8）客户数量、客户对货物的需求量、客户具体的收货位置、客户的期望时间窗以及每个客户需要服务的时间己知;

（9）所有的客户都能被任何一个车场的车辆服务，但每个客户仅仅可以被一辆车服务一次，且需求一次得到满足;

（10）客户配送地址发生改变，需求量不变;

（11）配送过程中货物的质量不会发生改变;

1.2   变量说明

[dij]：表示客户节点[i]到[j]的距离;

[C0]：表示车辆的单位运输成本;

[V0]：表示车辆的行驶速度;

[STi]：表示车辆在客户点[i]的服务时间;

[timk]：表示车场[m]的车辆[k]抵达客户[i]的时刻;

[[Ei，Li]]：表示客户[i]的期望时间窗;

[δ]：表示超出客户期望时间窗的最大忍耐时间;

[s]：表示还未收到货物的客户数量;

[V]：为点集合，[V=（v1，...，vs，vs+1，...，vs+k）]，[v1，...，vs]表示还未收到货物的客户，[vs+1，...，vs+k]表示当前送货车辆的位置，即虚拟配送中心;

[DP]：表示客户对于送货时间的不满意度;

[DF]：表示干扰事件发生后物流运营商的配送成本;

[DN]：表示路径偏离量;

[xmkij=1，车场m的车辆k从点i行驶到点j0，否则;]

[tmkij]：表示路径偏离参数，且

[tmkij=-1，原方案中有，新方案中没有的路径0，原方案以及新方案中均没有的路径1，原方案中没有，新方案中有的路径.]

1.3   扰动度量

本文假设客户的不满意度只跟客户收到货物的时间相关。当客户的收货时间在期望时间窗内时，客户的不满意度最低，当客户的收货时间提前或延迟于期望时间窗，会增加客户的不满意度，但客户不会选择拒绝收货。如图1：

图中当[Ei≤tmki≤Li]时，代表[m]车场的车辆[k]在客户的期望时间窗抵达，惩罚为0。当[Ei-δ<tmki<Ei]或者[Li≤tmki≤Li+δ]时表示货物没有在客户期望的时间内送到，需要进行相应的惩罚。因此，这里引用相应的惩罚函数[Pi（ti）][10]： [Piti=Max                         tmki<Ei-δ 或者 tmki>Li+δaiEi-tmkimi          Ei-δ≤tmki≤Ei0                              Ei≤tmki≤Libitmki-Lini           Li≤tmki≤Li+δ] （1）

其中：[ai]、[bi]、[mi]和[ni]均为惩罚系数。客户平均不满意度的计算方法如下：

[DP=i=1Nm=1Mk=1KmPi（ti）N] （2）

物流运营商最注重的是货物配送的成本，在车辆运输的过程中，由于某个客户配送地址发生改变，会导致未被服务的客户地址集合发生改变，因此配送路线也会和原计划有所不同，这将会对物流配送成本造成影响。物流运营商的成本扰动公式为：

[DF=k=1kmm=1Mi=1s+kj=1s+kC0dijxmkij] （3）

配送人员是货物运输的主要执行者，当客户的配送地点发生改变时，车辆行驶的路线也会发生相应的改变，这在一定程度上会影响配送人员的工作情绪，也会对配送的效率产生影响。路径偏离量扰动公式为：

[DN=k=1Kmm=1Mi=1s+kj=1s+ktmkij] （4）

1.4   干扰管理模型

根据以上三个干扰度量函数，建立多目标干扰管理数学模型如下：

[f1=min DP] （5）

[f2=min DF] （6）

[f3=min DN] （7）

[i=1sqij=1sxmkij≤Q，  k∈（1，2，...，Km）  ，m∈（N+1，N+2，...，N+M）] （8）

[j=1sm=1Mk=1Kmxmkij=1 ，  i∈S] （9）

[i=1sm=1Mk=1Kmxmkij=1 ，  j∈S] （10）

[i=s+1s+kj=1sxmkij=1，  k∈（1，2，...，Km）， m∈（N+1，N+2，...，N+M）] （11）

[i=1s+kxmkij=1，  k∈1，2，...，Km， j=m∈（N+1，N+2，...，N+M）] （12）

[Ei-δtmkiLi+δ，  i∈1，...，s，  k∈（1，...，Km）， m∈（N+1，...，N+M）] （13）

其中式（5）、（6）、（7）为目标函数，分别表示客户不满意度最低、物流成本最小、路径偏离最小;式（8）表示每辆车的装载量不可多于该车的最大运输量;式（9）和（10）表示一个客户仅仅可以被一辆车服务一次;式（11）表示每个辆车都在虚拟配送中心发车;式（12）表示车辆在送完货物后，回到初始车场;式（13）表示客户的时间窗。

2     多目标处理

针对多目标优化问题的处理，本文首先按照各目标之间的重要性给予对应的权重，然后对各目标函数进行规范化处理，将规范化处理后的目标函数乘以相应的权重，最后相加当作本文的目标函数，进而把多目标问题化简为单目标问题。

2.1   确定权重

为了保证权重赋值的客观性，本文按照各目标的重要性程度对权重进行随机化处理，在提高算法搜索能力的同时可以得到多个最优解。目标函数的权重[le]为：

[le=ran d1ran d1+ran de] （14）

其中，[0≤le≤1]，[e∈[1，3]]，[l1>l2>l3]，且[e=13le=1]，[ran de]为非负随机实数。

2.2   规范化处理

本文要求解的多个目标之间的量纲不是统一的，不能直接采用线性加权法进行求解。本文采用如下权重模型[11]对三个目标函数进行规范化处理。

[F=1-e=13le（fe-f*ef*e）] （15）

其中，[fe*]为第e个目标在单目标限制条件下的最佳配送路线的值，[F]越高说明配送路线越理想。本文将F作为最终的目标函数。

3     干扰管理模型的求解

车辆路径问题属于NP-hard问题。Karakatic等[12]在求解大规模的NP-hard问题上将几种启发式算法进行了比较，结果显示出遗传算法在处理大规模NP-hard问题上相比于其他启发式算法，更适用。遗传算法有着不错的容错性和隐含的并行性能等优势，但同时也有“早熟”的现象。所以，本文将遗传算法进行了一定的改进，使其能够适用于本文所构造的模型。

3.1   染色体编码与解码

本文选取基于客户点的整数编码方式，每条染色体是所有客户点的一组全排列。解码与编码相对应，是遗传算法中用来将搜索空间的可行解转换到解空间的方法。本文在解码的过程中，用“A、B、C”代表車场，在染色体中随机插入车场编号，并且确保每条染色体的起点和终点都是A、B或C，这代表每辆车从所属车场发车，完成任务后回到原车场。例如，解码染色体A1[123]AB3[456]BC2[789]C代表车辆的行驶路线，车场A编号为1的车辆路线为：A-1-2-3-A;车场B编号为3的车辆路径为：B-4-5-6-B;车场C编号为2的车辆路径为：C-7-8-9-C。经过不断的循环迭代，找到能够满足约束条件并且结果最好的解码方案，以此来制定新的配送方案。

3.2   初始化种群

为了能够使种群具有多样性，防止出现局部最优的情况，初始种群中[45]随机生成，其次，按照干扰管理的思想，新生成的方案对初始方案的扰动越小越好，所以剩余[15]部分的种群由初始方案的个体构成。

3.3   解的改善

为了加快最优解的求解过程，在算法中引入了迭代交换过程（Iterated Swap Procedure，ISP）[13]。以下是ISP的具体过程：

第一步：随机挑选一个父代中的两个基因点。

第二步：将挑选出来的两个基因点交换位置，形成1个子代。

第三步：在上一步的基础上再次将交换的两个基因点与相邻的基因点进行交换，产生4个子代。

第四步：从所有子代中挑选出最优的子代。

第五步：如果最优子代好于父代，则用子代代替父代，返回第一步;否则停止ISP过程。

ISP的具体实施过程见图2。

3.4   适应度函数

本文选取式（15）作为适应度函数。

3.5   选择

为了避免造成较大的选择误差，本文使用轮盘赌选择以及最佳保留选择相结合的办法，在减小选择误差的同时，又提高了收敛的速度。

3.6   交叉变异操作

本文的交叉变异操作引用了文献[14]中的自适应算子，该方法可以很好的防止遗传算法早期容易“早熟”的问题，并且提高了算法在中后期搜索的速度。

（1）交叉操作

本文采用顺序交叉，交叉概率并不是一个不变的值，而是根据每代种群中最佳个体的适应度值和其它个体之间的差额关系决定的。交叉概率公式见下式：

[pc=11+exp（k（min-f））] （16）

式中：[min]是个体的最小适应值，[f]是种群中所有适应度值低于平均适应度值个体的均值。[k>0]，[exp（  ）]为以[e]为底数的指数函数。因为[min-f<0]，所以[0<exp（k（min-f））<1]。当[min]越靠近[f]，表示种群内的适应度值差异越小，则[pc]越靠近于0.5，此时优秀个体的染色体结构能够保持稳定，减少了求解的时间。当[min]越偏离[f]，表示种群内适应度差异越大，则[pc]越接近于1，此时有助于依靠交叉形成新的个体，扩大了搜寻空间。

（2）变异操作

本文选用调换两点间基因值的变异方法，变异概率并不是一个不变的值，而是根据每代种群中最佳个体的适应度值与其它个体之间的差额关系决定的。变异算子公式见下式：

[pm=1-11+exp（k（min-f））] （17）

式中：[min]是个体的最小适应值，[f]是种群中所有适应度值低于平均适应度值个体的均值。[k>0]，[exp（    ）]为以[e]为底数的指数函数。因为[min-f<0]，所以[0<exp（k（min-f））<1]。当整体收敛性高，个体间适应度值差距小时，[exp（k（min-f））]越接近1，则[pm]就越接近于0.5，这时有助于增大变异概率产生新的个体。当整体收敛性低，个体间适应度值差距大时，[exp（k（min-f））]越接近0，则[pm]就越接近0，降低了求解的速度。

4     模型仿真及分析

本文的仿真实验在MATLAB 2016a版本上进行操作，操作环境为Intel Core i3-3217U 1.80 GHz （8.00 GB RAM），操作系统为64位Win8.1。遗传算法的种群规模为80，迭代次数为100。时间窗惩罚参数设置如下：[ai]=0.05，[bi]=0.5，[mi]=0.02，[ni]=0.03。

4.1   初始设置及初始配送路线

以某物流公司的配送任务对模型进行求解计算，车场的数量[M]为3，每个车场配备2辆相同型号的车辆，客户点的数量[N]为16，车速[V0]为40 km/h，车辆的单位运输成本[C0]为每公里5元。具体的数据见表1。

其中，3个车场的具体坐标分别为（20，20），（75，45），（50，80），每辆车的最大运输量为9t。

16个客户地址的具体坐标、货物需求量、客户期望的时间窗以及服务每个客户所需要的时间，如表2所示。

根据初始配送要求，求出初始配送路线，见表3。

其中，车场1、车场2、车场3分别用A，B，C来代表，每辆车从各自的车场出发，完成配送任务后回到初始的车场。

4.2  干扰分析

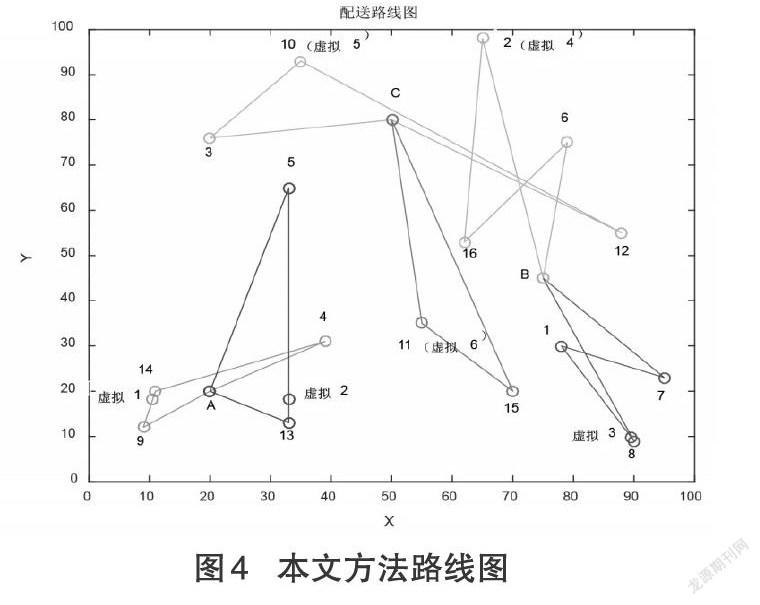
货车运输的过程中，当[t=2h]时，客户15的配送地点发生变动由[73，85]变为[70，20]，此时若按原计划继续进行配送，客户15的时间窗则得不到满足，会大大增加客户的不满意度。本文在不考虑有其他车辆救援的情况下，将本文方法与重调度法得到的结果进行对比分析，两种方法求解的结果见表4，行驶路径见图3、图4。

4.3  對比分析

经过对比重调度法和本文的方法能够得出结论：

（1）从客户的利益来看，本文的方法在客户不满意度方面比重调度法降低了7%，这表明本文的方法在减少客户不满意度方面的效果是显著的。

（2）从运营商的利益来看，虽然本文的方法在物流成本上高于重调度法，但是相差不多。

（3）从配送人员的利益来看，本文的方法在路径偏离方面比重调度法减少了2条路径，这说明本文的方法在减少路径偏离方面优于重调度法。

综上，重调度法仅仅依据成本最小为目的来规划配送路线，虽然比本文的方法具有较低的配送成本，但却大大提高了客户的不满意度。而本文的方法以增加少许的物流成本为代价，有效的减少了客户不满意度和路径偏离数。从物流运营商的长期利益来看，使用本文的方法虽然会增加少量的物流成本，但能提高客户和配送人员的利益，有助于物流运营商与客户维持长期的合作关系，使物流运营商能够持久盈利。

5     结语

本文基于干扰管理的思想，探讨了因客户配送地址变动的多车场车辆调度问题。以现有的车辆调度干扰管理模型为基础，综合考虑了客户，物流运营商以及配送人员三个主体的利益，设计了适合本文研究的多车场车辆调度干扰管理数学模型。并对遗传算法进行了改进，使算法更适用于求解本文的干扰管理模型，经过仿真检验了本文算法的可行性。本文是干扰管理在多车场车辆调度领域的成功运用，为求解多车场领域干扰管理难题进行了有益的探索。

须指出的是，在现实生活中物流运输的过程必然伴随着多种扰动因素，因此，将多种干扰因素相结合是下一步研究的方向。

[参考文献]

[1] Zhou L，Baldacci R，Vigo D，et al. A Multi-Depot Two-Echelon Vehicle Routing Problem with Delivery Options Arising in the Last Mile Distribution[J]. European Journal of Operational Research，2017，265（2）： 765-778.

[2] Afshar-Nadjafi B，Afshar-Nadjafi A. A constructive heuristic for time-dependent multi-depot vehicle routing problem with time-windows and heterogeneous fleet[J]. Journal of King Saud University-Engineering Sciences，2017，29（1）： 29-34.

[3] 顏瑞，朱晓宁，张群，等. 考虑二维装箱约束的多车场带时间窗的车辆路径问题模型及算法研究[J]. 中国管理科学，2017，25（7）： 67-77.

[4] Mirabi，Mohammad. A hybrid electromagnetism algorithm for multi-depot periodic vehicle routing problem[J]. The International Journal of Advanced Manufacturing Technology，2014，71（1）：509-518.

[5] Suzuki Y. A dual-objective meta heuristic approach to solve practical pollution routing problem[J]. International Journal of Production Economics，2016，176（30）： 143-153.

[6] 毕志升，郑炯彬，蔡桂艳. 基于高维多目标优化的多车场车辆路径问题[J]. 计算机与数字工程，2017，45（7）： 1298-1304.

[7] 王旭坪，吴绪，马超，等. 运力受扰的多车场车辆调度干扰管理问题研究[J]. 中国管理科学，2010，18（6）： 82-88.

[8] 王征，王建军，杨文超. 顾客时间窗变化的多车场车辆调度干扰管理模型研究[J]. 管理科学，2010，23（3）： 103-112.

[9] 郑丹阳，毛剑琳，郭宁，等. 多车场动态路径问题的自适应量子蚁群算法[J]. 传感器与微系统，2017，36（10）： 133-136.

[10] 丁秋雷 胡祥培，姜洋. 物流配送受扰延迟问题的干扰管理两阶段决策方法[J]. 运筹与管理，2012，21（6）： 84-93.

[11] 郭森，秦贵和，张晋东，等. 多目标车辆路径问题的粒子群优化算法研究[J]. 西安交通大学学报，2016，50（9）： 97-104.

[12] Karakatic S，Podgorelec V. A survey of genetic algorithms for solving multi-depot vehicle routing problem [J]. Applied Soft Computing，2015，27（1）： 519-532.

[13] Ho W，Ji P. Component scheduling for chip shooter machines： a hybrid genetic algorithm approach [J]. Computers and Operations Research，2003，30（14）： 2175-2189.

[14] 符俊波，马慧民，张爽，等. 有垃圾量变动的生活垃圾收运车辆调度干扰管理研究[J]. 上海理工大学学报，2017，39（4）： 368-375.