具有渐开线齿廓变形后的柔轮三维实体建模方法

莫瀚宁 邱辰

摘要：行星式波发生器微型谐波齿轮传动的柔轮具有内外齿圈。推导出变形柔轮齿廓上点的坐标与未变形柔轮齿廓上点的坐标的转换关系，进而利用MATLAB编程求解变形柔轮四分之一内外齿圈各轮齿两侧齿廓上各点的坐标，在Pro/E中对四分之一内外齿圈齿廓上的点用样条曲线连接，并通过镜像和拉伸，完成变形柔轮的三维实体建模。

关键词：谐波齿轮传动;柔轮;实体建模;有限元

中图分类号：TH132.4                                     文献标识码：A                                文章编号：1674-957X（2021）14-0008-03

0  引言

在谐波齿轮传动中，波发生器使柔轮发生弹性变形，变形后的柔轮与刚轮啮合，当波发生器旋转时，借助于柔轮上流动的弹性波，实现运动的转换。为完成谐波齿轮传动整机的动静态特性分析，在对谐波齿轮传动整机进行三维装配建模过程中，必须涉及到变形后柔轮的三维建模，由于变形柔轮中线上各点法线的旋转，相对未变形柔轮，其齿圈上的轮齿也将发生偏转，因此变形后柔轮的三维建模涉及到其齿圈上不同位置轮齿的三维建模，这一般需要通过对未变形柔轮及其轮齿齿廓数据进行坐标变换才能得到，行星式波发生器微型谐波齿轮传动中的柔轮具有内外齿圈。本文主要阐述了柔轮变形下三维模型的构建。

1  建立坐标系

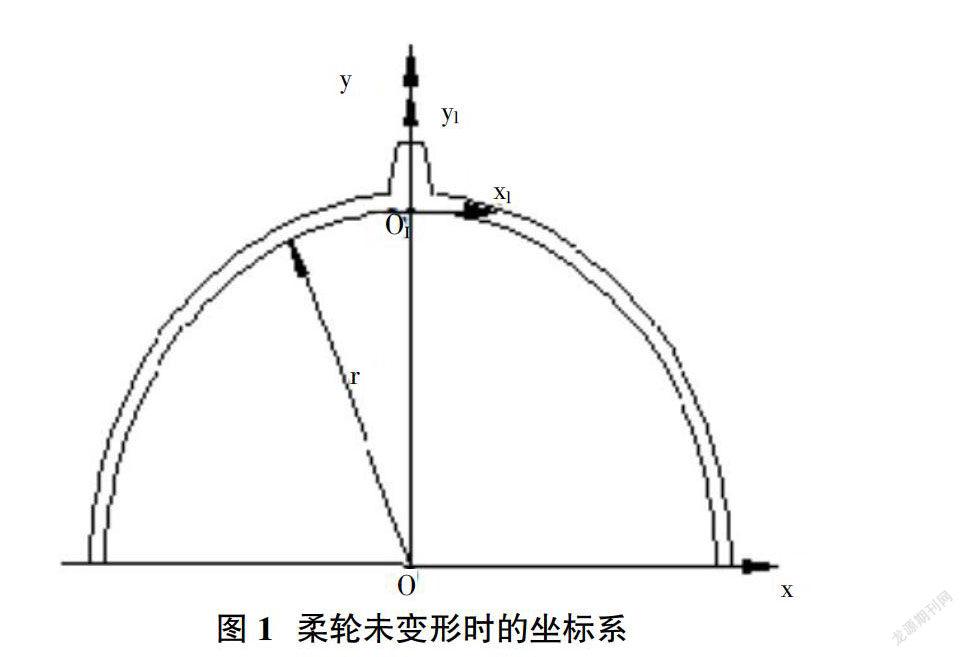
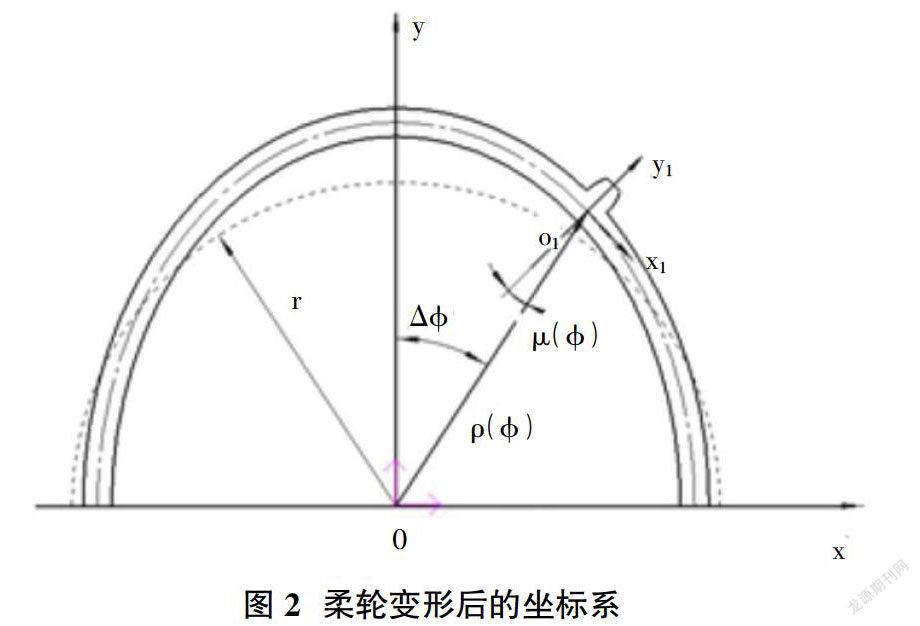
建立柔轮未变形时的坐标系如图1所示。固定坐标系oxyz建立在刚轮上，以刚轮的几何中心为坐标原点o，以刚轮轮齿的对称轴线为y轴，z轴按右手定则来确定。运动坐标系o1x1y1z1建立在柔轮上，以柔轮轮齿的对称轴为y1轴，以y1轴和原始曲线的交点为坐标原点o1。柔轮变形后，坐标系如图2所示。r（j）为对应长轴角坐标为j处，变形柔轮上O1点的矢径，m（j）为该点的法线转角。

1.1 齐次坐标变换矩阵

设变形柔轮齿廓上某点p在运动坐标系{1}中表示为1P=[x1，y1-r，0，1]T，在固定坐标系中表示为0P=[x0，y0，z0，1]T，则：

其中，

（2）

1.2 未变形柔轮轮齿渐开线齿廓上各点的坐标

由参考文献2，渐开线左侧齿廓方程（对内齿轮为齿槽的左侧齿廓）为：

右侧齿廓方程（对内齿轮为齿槽的右侧齿廓）为：

式中，？琢为未变形柔轮分度圆处的压力角，？琢=20°，u=tan？琢k-tan？琢，对外齿圈，？兹=s/2r;对内齿圈，？兹=e/2r。？琢k为未变形柔轮渐开线齿廓上任意一点处的压力角，r0为未变形柔轮的分度圆半径;s和e分别为未变形柔轮的外齿圈齿厚和内齿圈齿槽宽。

1.3 变形柔轮轮齿齿廓上各点的坐标

由参考文献3，对于双滚子式发生器，变形柔轮的公式为：

2  变形柔轮轮齿齿廓上各点坐标值数据的预处理

第一步：求解未变形柔轮内外齿圈单个轮齿两侧齿廓上点的坐标。

第二步：在变形柔轮四分之一内外齿圈上，求解ψ，μ，ρ，ω。

第三步：求解变形柔轮四分之一内外齿圈各轮齿两侧齿廓上点的坐标。

第四步：将分布在变形柔轮四分之一内外齿圈上的各轮齿两侧齿廓上点的坐标，按顺序依次排列，使得在Pro/E中能够用样条曲线将它们按顺序连接起来，以得到变形柔轮四分之一内外齿圈的轮廓曲线。

第五步：将变形柔轮四分之一内外齿圈上各轮齿两侧齿廓上点的坐标，分别列成两个表格，并另存为Pro/E的点文件，以导入Pro/E中。

3  Pro/E环境下变形柔轮的三维建模

3.1 变形柔轮三维模型的建立

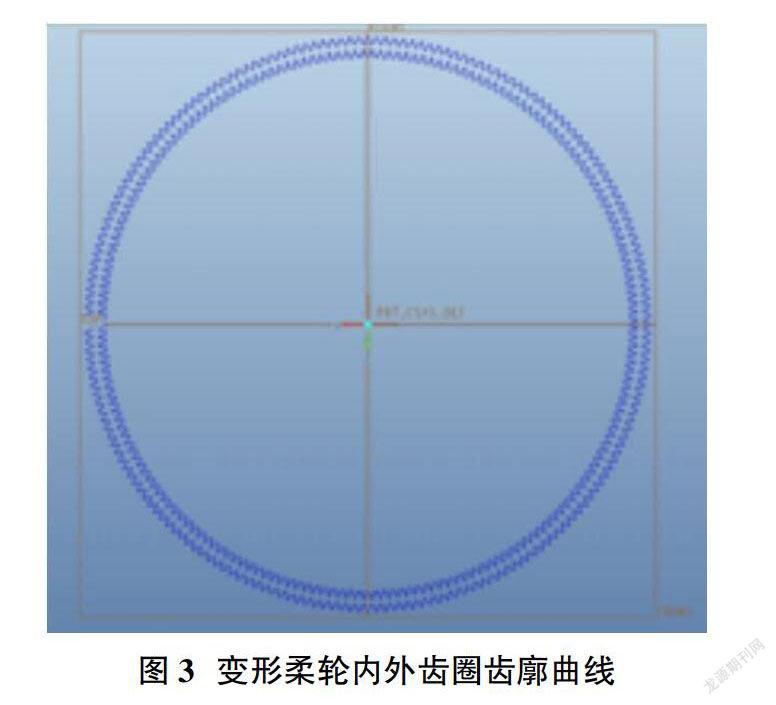
在Pro/E环境下，首先导入已经另存为Pro/E点文件的变形柔轮四分之一外齿圈各轮齿两侧齿廓上的各点坐标。然后利用样条曲线将这些点按顺序依次连接起来得到变形柔轮的四分之一外齿圈齿廓曲线，在通过镜像以形成变形柔轮完整的外齿圈齿廓曲线。由变形柔轮外齿圈齿廓曲线的生成方法用样条曲线将导入的柔轮内齿圈齿廓数据连接成曲线同样可得其内齿圈齿廓曲线。变形柔轮内外齿圈曲线如图3所示。最后通过拉伸操作形成柔轮。三维实体模型，如图4所示。

3.2 变形柔轮与行星轮的装配检验

建立变形柔轮和刚轮行星轮的三维装配如图5（a）所示，其轮齿啮合细节分别如图5（b）和图5（c）所示，对变形柔轮和行星轮进行装配干涉检验变形柔轮和行星轮装配时轮齿啮合没有出现干涉现象。

3.3 柔轮的静力有限元分析

为分析双滚子齿轮系的柔轮应力状况，取四分之一柔轮并施加位移载荷得到柔轮的应力云图和位移云图分别如图6和图7所示。

根据图6，齿对齿柔轮的最大应力为367.501MPa，最小应力为0.163442MPa。根据图7，齿对齿柔轮的最大位移为0.04mm，最小位移为-0.04mm。最大應力与最大位移均发生在柔轮长轴和波发生器接触的地方。最大应力出现在最靠近柔轮长轴的轮齿之间的齿根处。

4  总结

变形柔轮三维建模的关键在于建立其齿廓上点的坐标在变形前与变形后的关系，根据这些关系利用MATLAB编程分别求解变形柔轮四分之一内外齿圈各轮齿两侧齿廓上各点的坐标，并存为Pro/E点文件，然后在Pro/E中，用样条曲线连接这些点，并对四分之一内外齿圈齿廓曲线进行镜像和拉伸，最终完成变形柔轮的三维实体建模。该模型对于分析微型谐波齿轮传动整机动静态特性具有重要意义。

参考文献：

[1]乔绪维.微型谐波齿轮传动设计与性能分析[D].北京工商大学，2011.

[2]沈允文，叶庆泰.谐波齿轮传动的理论和设计[M].机械工业出版社，1985.

[3]M.H.伊万诺夫.谐波齿轮传动[M].国防工业出版社，1987.