S355钢焊接温度场和应力场有限元分析
段卫军 邓鸿剑 陈北平











摘要:S355钢作为低合金钢,在焊接过程中会伴随着固态相变现象。在考虑S355钢的固态相变效应基础上,建立了焊接过程的热弹塑性有限元模型。通过引入相变转变模型、相变塑性和相变体积模型,计算获得焊后组织分布云图,并分析了焊缝和热影响区典型节点的组织演变规律。结果表明,与不考虑固态相变效应相比,紧邻焊缝两侧的热影响区的Mises应力大幅降低,计算得到的残余应力值与实测值吻合较好。
关键词:S355钢;固态相变;微观组织;残余应力
0 前言
S355钢属于低合金高强钢,其综合力学性能优良、淬透性优异,被广泛用于工程制造中。在低合金钢的焊接过程中,由于局部不均匀的热源作用产生的热应变,并伴随着固态相变现象,以及因固态相变引起的体积变化和相变诱导塑性效应等,导致工件冷却后形成复杂的焊后残余应力[1]。研究S355钢的焊接应力的工程应用具有重要意义。
目前广泛采用有限元分析技术对关键结构的焊接过程温度场和应力场演变进行研究。Deng等人[2]研究了固态相变对9Cr-1Mo钢管对接焊残余应力分布的影响,发现马氏体相变引起的体积变化不仅影响残余应力的大小,而且还使得部分区域由拉应力转变成了压应力。迟露鑫[3]对SA508-3钢厚壁圆筒进行了多层多道焊,发现热源作用区域的温度梯度变化很大,圆筒外壁的残余应力明显大于内壁的残余应力。Jiang等人[4]研究了低温相变焊丝对残余应力的影响,证实马氏体转变引起的间断冷却收缩显著降低了残余应力。Hamelin等人[5]进行了铁素体钢单道焊接的试验和有限元模拟,发现当接头中存在马氏体相变时,相变塑性对应力场有显著影响。
文中以S355钢为研究对象建立了考虑固态相变效应的热-组织-应力的有限元模型,进行焊接过程中的温度场和应力场的有限元分析。
1 试验方法
试验母材为S355钢,焊丝为GM55-II。采用激光焊进行平板对接焊,其中设备为TRUMP-10002蝶式激光器,激光为连续激光,波长1 060 nm,斑点直径0.2 mm,焊接时采用负离焦量(-2 mm)。
焊接试件坡口形式如图1所示。采用单道次激光焊接,焊接工艺参数如表1所示。焊后采用盲孔法测试残余应力。
2 有限元模型
2.1 网格模型
网格模型如图2所示,尺寸150 mm×150 mm×12 mm。对焊缝区域的网格进行了局部加密,其他区域采用过渡网格。单元类型为六面体单元,焊缝及热影响区网格尺寸为0.5 mm,母材网格尺寸1~5 mm过渡。母材和焊材的热物理性能和热机械性能见表2。
2.2 热源模型
由于文中采用的激光功率较大,存在两种效应:一是激光在坡口上部填充焊丝熔化形成熔池的热导焊,二是激光穿透形成小孔的深熔穿透焊,最终两种效应组合形成高脚杯形状的焊缝。
为准确拟合激光焊接传热过程的熔池形态,采用双椭球热源+圆锥体积热源组成的复合热源模型。其中双椭球热源模型的分布模型如式(1)所示:
式中 Q=ηUI,η为热效率,U和I分别为电压、电流;ff和fr分别为前、后两个半椭球体的能量分配系数,令ff∶fr=3∶7;a、bf、br、c为形状参数。
锥形热源的模型如式(2)所示:
式中 r0为有效作用半径;r为节点与热源中心之间的距离;m为线性衰减系数;H为热源作用深度;h为任意截面的高度。
2.3 相变数学模型
2.3.1 组织转变数学模型
2.3.2 相变塑性和相变体积模型
式中 βA-F和βA-M分别为奥氏体向铁素体和马氏体转变的相变膨胀系数;βT-A为奥氏体化过程中的相变收缩系数;dfF、dfM和dfA分别为铁素体、马氏体和奥氏体体积分数的增量形式。
不同相的相膨脹系数和相变体积变化系数可由CCT测试中的膨胀曲线获得,如图4所示。
3 结果与分析
3.1 焊接传热分析
单道焊接工艺的温度场分布如图5、图6所示,复合热源可以较好地反映激光焊的深熔效果。
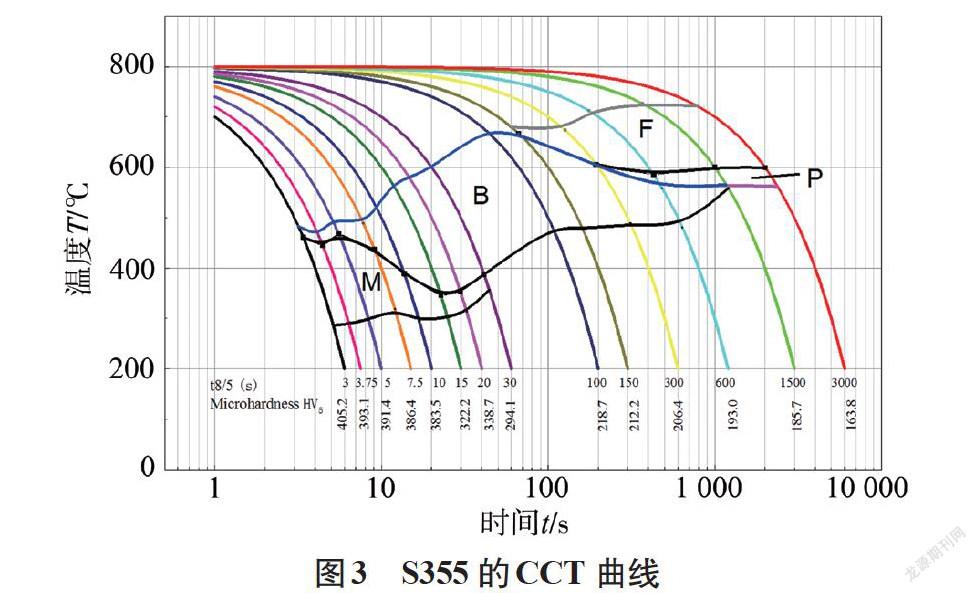
距焊缝中心不同距离的节点在焊接过程中的热循环曲线如图7所示,求得所有点在800~500 ℃区间的冷却速度均在250~100 ℃/s之间。根据文中材料的测试结果,该冷速下只会发生马氏体相变,不会发生铁素体、珠光体和贝氏体相变。
3.2 焊接过程相变转变
结合温度分布云图(见图8)可知,焊接熔池及热影响区(温度高于Ac3)中奥氏体占比100%;温度降至Ms以下的区域均发生了马氏体相变,其中起焊处奥氏体已经全部转变为马氏体。最终焊缝及热影响区全部由马氏体组成。
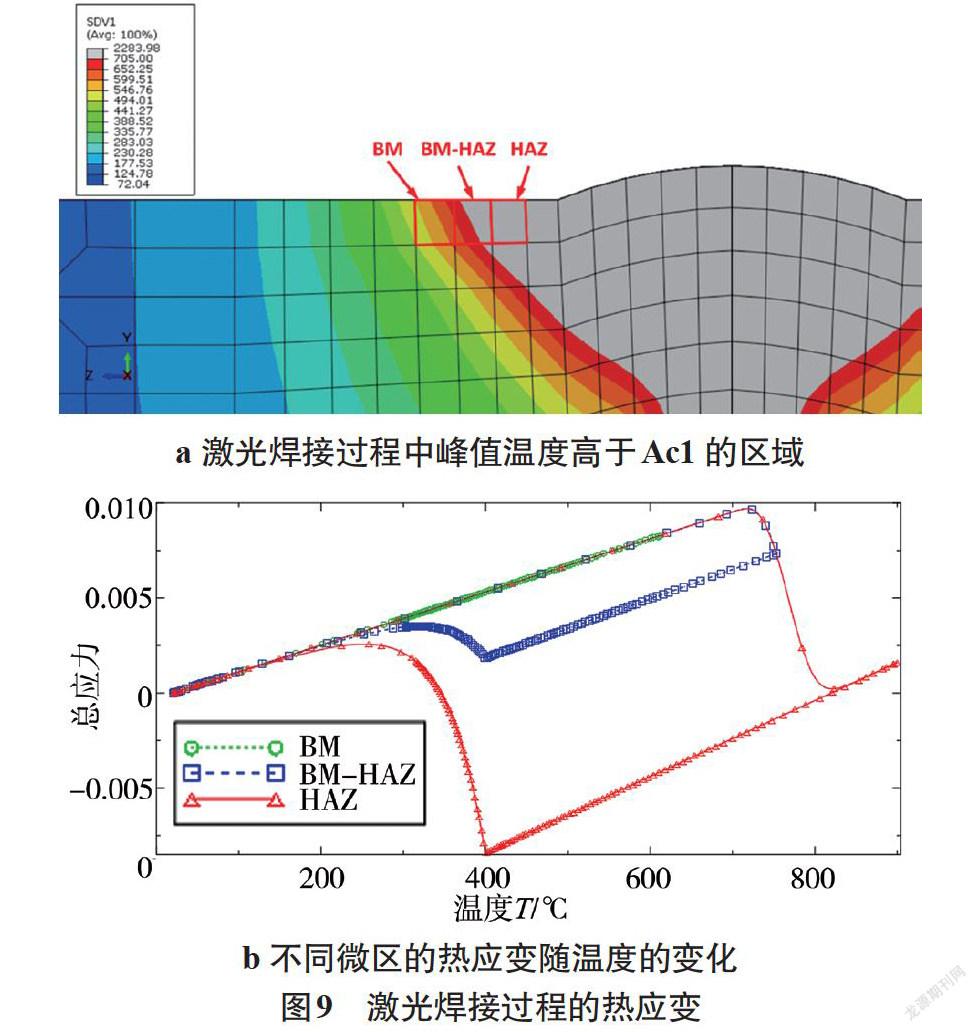
从热影响区与母材交界面横向取3个相邻单元,提取其热应变的计算结果与温度结果绘制出热应变转变曲线,如图9所示。可以看出,母材区单元(绿色)由于温度始终未超过Ac1,所以未发生相变,焊接时热应变随温度线性增加,冷却时又沿原路线性降低。热影响区单元(红色)升温到Ac1~705 ℃后,发生奥氏体转变,体积收缩,总应变陡降,超过Ac3~856 ℃时转变完成;冷却时,未发生任何扩散型相变,直至Ms~399.5 ℃点以下,发生马氏体相变;冷至室温后,最终热应变归零。母材与热影响区交界面上的单元(蓝色)在升温时,峰值温度未超过Ac3,所以只有少部分转变为奥氏体;冷却时,只有这部分奥氏体在Ms点以下发生了马氏体相变,而其余部分仍为母材状态。
3.3 相变对焊接变形的影响
考虑相变时,激光焊接的最终变形如图10a所示,角变形比较明显,而纵向弯曲趋势不明显。熄弧端的角变形略大于起弧端。不考虑相变时(见图10b),单道焊的角变形略大于考虑相变的计算结果,此外呈现出非常明显的纵向弯曲。
3.4 相变对焊接残余应力的影响
计算得到的激光焊接残余应力如图11所示。考虑相变时(见图11a),整个板厚上均呈现熔合区纵向受压、热影响区与母材交界面纵向受拉、母材远端纵向受压的状态,最大纵向压应力出现在熔合区中间,最大纵向拉应力出现在1/2厚度处的热影响区与母材交界面上;而不考虑相变时(见图11b),整个板厚上均呈现熔合区和热影响区纵向受拉、只有母材受压的状态,且熔合区纵向拉应力大于热影响区。由此可见,考虑相变时,应力水平较高的焊缝附近区域拉、压应力获得部分抵消,焊缝的纵向收缩合力小于不考虑相变的情况,导致后者纵向弯曲变形明显大于前者。其中考虑相变计算得到的焊接纵向应力和盲孔法测试得到结果具有较好的一致性,如图12所示。
4 结论
考虑固态相变效应后,进行S355钢激光焊接过程中热-组织-应力演变过程有限元模拟,得到以下结论:
(1)通过模拟,得到了焊缝及热影响区经历焊接热循环条件下的马氏体转变规律。
(2)在固态相变作用下,激光焊接变形和残余应力显著降低。仿真得到的应力分布规律与实测值吻合较好。
参考文献:
Kumar S,Singh P K,Karn K N,et al. Experimental investigation of local tensile and fracture resistance behaviour of dissimilar metal weld joint: SA508 Gr.3 Cl.1 and SA312 Type 304LN[J]. Fatigue & Fracture of Engineering Materials & Structures,2017,40(2):1-17.
Deng D,Murakawa H. Prediction of welding residual stress in multi-pass butt-welded modified 9Cr-1Mo steel pipe considering phase transformation effects[J]. Computational Materials Science,2006,37(3):209-219.
遲露鑫,麻永林,邢淑清,等. 核电SA508-3钢厚壁圆筒纵向焊接残余应力分析[J]. 焊接学报,2012,33(6):59-62+67,116.
Jiang W C,Chen W,Woo w,et al. Effects of low-temperature transformation and transformation-induced plasticity on weld residual stresses:Numerical study and neutron diffraction measurement[J]. Materials and Design,2018(147):65-79.
Hamelin C J,Muránsky,Smith M C,et al. Validation of a numerical model used to predict phase distribution and residual stress in ferritic steel weldments[J]. Acta Materialia,2014(75):1-19.
Chen X Z,Fang Y Y,Li P,et al. Microstructure, residual stress and mechanical properties of a high strength steel weld using low transformation temperature welding wires[J]. Materials and Design,2015(65):1214-1221.
Seong-Hoon K,Yong-Taek Im. Three-dimensional finite-element analysis of the quenching process of plain-carbon steel with phase transformation[J]. Metallurgical and Materials Transactions A,2005,36(9):2315-2325.
张丽芳. 高Cr铁基合金连续冷却固态相变与动力学模拟[D]. 天津:天津大学,2012.
Tatsuo Inoue. Mechanics and Characteristics of Transforma-tion Plasticity and Metallo-thermo-mechanical Process Simulation[J]. Procedia Engineering,2011(10):3793-3798.
Cory J Hamelin,Ondrej Muránsky,Michael C,et al. Valid-ation of a numerical model used to predict phase distribution and residual stress in ferritic steel weldments[J]. Acta Materialia,2014(75):1-19.
Ronda J,Oliver G J. Consistent thermo-mechano-metallur-gical model of welded steel with unified approach to derivation of phase evolution laws and transformation-induced plasticity[J]. Computer Methods in Applied Mechanics and Engineering,2000,189(2):361-417.

