SolidWorks Motion冗余约束和运动算例报错分析
柯治成
关键词:SolidWorks Motion;自由度;冗余约束;报错分析
0引言
机构的运动分析是了解机械运动性能的必要手段,传统机械设计常采用理论力学的方法计算运动学或动力学特性,这种方法对复杂机构具有局限性。
目前随着CAE技术的飞速发展,虚拟样机仿真工具SolidWorks Motion得到了广泛应用。其借助工业动态仿真分析软件ADAMS的求解器来分析装配体的复杂行为,可与SolidWorks三维建模实现无缝集成,并通过约束映射将零件之间的配合(约束)自动映射为Motion中的连接,节约运动分析时间。鉴于传统机械设计的局限性和ADAMS软件建模、实操性差的缺点,同时结合现代机械产品开发要求,应用solidWorks Motion就能对虚拟样机进行运动学和动力学分析,易学易用。可在设计前期判断设计是否达到预期目标,有利于缩短产品开发周期,增强市场竞争力。
1约束方程及自由度计算
空间中未受约束的刚性实体具有6个自由度。当两个刚性实体之间添加配合时,每个配合都将移除实体之间一定数量的自由度,限制了部件间的相对运动。solidWorks Motion中的约束通过在微分一代数方程(Differential and A1gebmic equalions,DAE)的控制系统中添加代数约束方程,从系统中移除自由度(DOF)。代数方程描述被配合约束的自由度,以“i”标记在第一个零件上,“j”标记在第二个零件上。
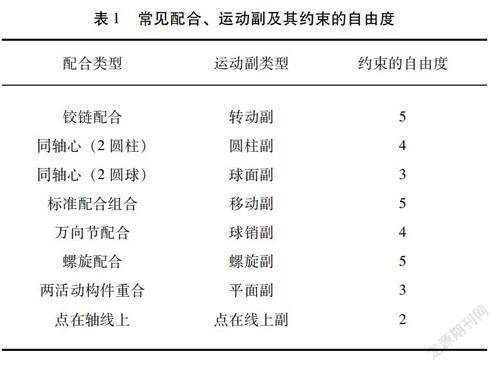
常见配合、运动副及其约束的自由度如表1所示。
根据Gruebler自由度的估算值判断系统是否过约束:如果Gruebler>0,模型为欠约束(动力学);如果Gruebler=0,模型为全约束(运动学);如果Gruebler<0,模型为过约束(冗余)。
上述计算没有考虑机构中运动副的连接、方向是否正确及冗余情况,实际自由度数如下所示。
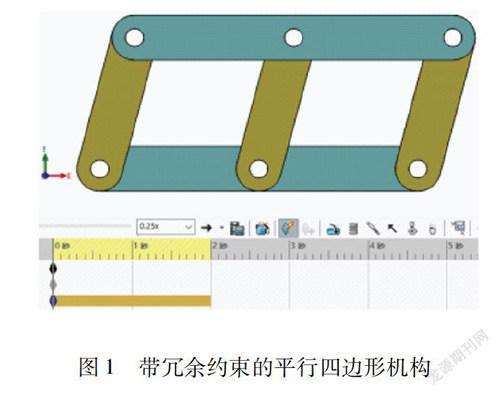
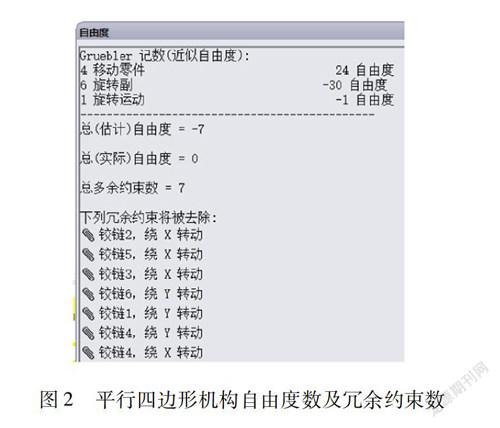
下面以带冗余约束的平行四边形机构为例,如图1所示。机构由4个活动构件组成,添加了6个铰链配合(转动副)和1个旋转驱动(添加了1个约束)。Gruebler公式估算的自由度数为-7(4×6-6×5-1),因Gruebler<0,故该机构存在冗余约束。并给出实际自由度数为0(4x6-6x5-1+7)。机构中的自由度数及冗余约束数如图2所示。
2冗余约束概述及机构中的冗余约束
2.1冗余约束概述
SolidWorks提供了多种约束,包括高副约束和低副约束等,当机构中某一指定的自由度添加了多余的约束,即运动副带入的约束对机构的运动只起重复约束作用,这类约束称为冗余约束(又称虚约束)。
2.2机构中的冗余约束常发生在下列情况
(1)机构中,转动副连接的是两构件上运动轨迹相重合的点,则该连接将带人一个冗余约束。
(2)机构中,双转动副杆连接的是两运动构件上距离始终保持不变的两点。
(3)不影响机构运动传递的重复部分所带人的约束。
(4)机构中两构件构成多个移动副且导路互相平行。
(5)机构中两构件构成多个转动副且轴线互相重合。
(6)闭链机构。特别是平面闭链机构,普遍存在过约束。如:四棒连杆具有闭环,Gruebler=-3(3x6-4x5-1),有3个冗余配合。因环的每个边(从地面开始)约束连接杆以停留在装配体基准面中。
3冗余约束的移除方法
3.1机构装配关系前处理
运动仿真前打开装配体,检查下面几项。
(1)运动部件是否错误地设置成了固定。
(2)是否运行运动轨迹干涉检查。
(3)将有下层的构件(原动件或从动件)作为一个子装配体添加到机构中,减少机构中构件数及约束。
(4)分析刚性零件之问的配合,删除过定义的约束。
3.2将一起运动的零件设置到“刚性组”
通过选择零部件并将其分组到刚性组,组中的多个零部件将被视为一个零部件。具有下述特点:
(1)组中零部件间的运动和配合被忽略;
(2)刚性组的质量和惯性矩是组中所有零件值之和。
利用刚性组可减少机构中的配合,降低冗余约束,节省Motion分析的仿真时间。
3.3以套管替换配合
在运动算例中使用套管等于添加柔性配合来取代数学上的刚性配合,配合的刚度在各自的方向决定了反作用力的分布,可計算冗余配合处的力。可将套管设想为包含有一些松弛度的弹簧和阻尼系统。
可通过以下两种方式实现:
(1)在运动算例属性中选择以套管替换冗余配合选项,这种方法适合大多数情况;
(2)对配合进行“编辑特征”,在PropertyManager界面中选择“分析”,勾选套管并指定参数。
使用套管会减缓求解速度,且最佳的配合刚度和阻尼特性参数不易获取,仅在其他方法之后使用。
3.4以配合本原替换冗余
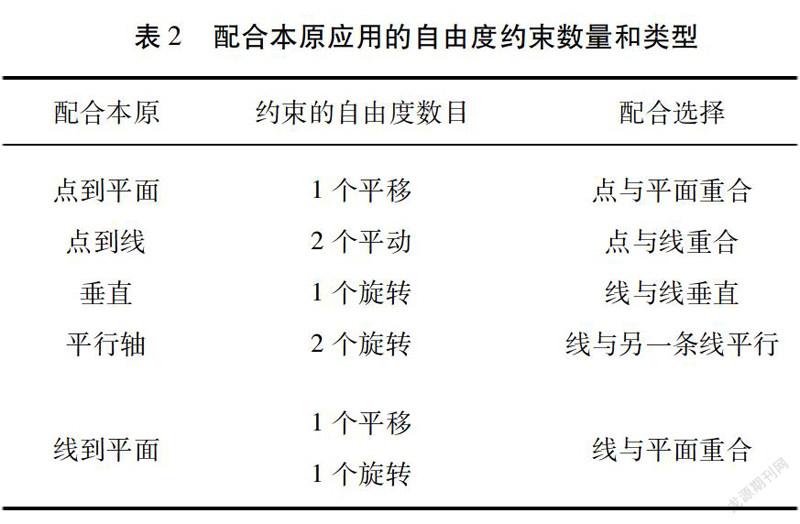
配合本原是指约束至少2个自由度的配合。通过用配合本原替换配合,可以删除零部件上的冗余约束,方法是逐个限制零部件上的自由度。表2所示为由零部件上的配合本原应用的自由度约束数量和类型。
替换配合本原是一个手动过程,需在模型上建立配合要素(点、轴线、基准面等),并要详细了解预期的运动。同时,需正确定向配合本原,以便优化约束缩减。配合本原在机构中的应用举例如下:
(1)一个平面到平面的重合配合(3个约束)可用线到平面的配合本原(2个约束)替换;
(2)铰链配合(5个约束)可用点到线(2个约束)和线到平面(2个约束)的配合本原替换;
(3)同轴心配合(2圆柱类型,4个约束)可用点到线的配合本原(2个约束)替换。
3.5运用模拟量
模拟量是SolidWorks自带的Motion插件中的虚拟动力源(电动机)部分,该动力源包括线性马达、旋转马达等。具体实现方式是将模拟量的运动参数设置为“0”,以单独约束构件在某个方向的自由度,避免出现冗余。如:通过线性马达约束指向的一个移动自由度,通过旋转马达约束指向的一个旋转自由度。
3.6以铰链配合替换形成铰链的冗余配合对
铰链是指两构件之间的相对运动为转动的运动副。铰链配合可将两个零部件之间的移动限制在一定的旋转范围内,此外还可以限制两个零部件之间的移动角度。铰链配合具有下述优点:
(1)建模时只需应用一个配合(替代重合和同轴心);
(2)运动分析的反作用力和结果与铰链配合相关联,而不是与某个特定的同心或重合配合相关联,这可减小冗余配合对分析的负面影响。
4运动算例计算
4.1SolidWorksMotion求解原理
Motion分析使用MAC ADAMS求解器2010簡化版,但求解时必须已知构件速度、连接构件的配合和力与加速度。在每个时间步长中,程序使用改进的Newton-Raphson迭代法进行求解。通过非常小的时间步长,根据零件的初始状态或前一时间步长的结果,软件可以预测下一时间步长内零件的状态,运算结果不断迭代直到满足预定的精确度。
4.2运动算例常见纠错步骤
(1)查看计算求解报错信息;
(2)压缩部分或所有驱动要素,时间轴位于0时刻;
(3)在装配体中通过移动零部件工具来检查修改,并确保机构能够正常运动;
(4)逐个解压之前压缩的驱动要素,并检查修正,确保机构能够正常拖动;
(5)每次更改都需要重新计算,修正至无报错信息。
4.3运动算例计算报错常见原因
4.3.1机构存在过多的冗余约束
仿真运行前如果积分器检测到机构包含冗余,将按旋转约束-平移约束-运动输入(马达)的次序移除冗余。移除成功后,积分器才继续运行仿真。在每一时间步,积分器重新评估冗余并在需要时将其移除。如果都失败,积分器将终止求解,并用报错信息(The model contains incompatibleredundant constraints…)通知用户检查机构中的冗余约束或不相容的约束(是否处于一个锁定位置)。可在Motion Manager中查看冗余约束详细说明,按第3章方法解除冗余。
4.3.2运动输入不连续
运动输入不连续会导致积分器终止求解,报错信息(…Check for discontinuity in motion inputs.)一般在计算的前段时间内出现。通常有两方面原因。
(1)驱动马达的位移、速度、加速度输入不连续。驱动马达控制一个构件在一段时间内的运动状况,其规定了构件的位移、速度和加速度为时问的函数。可通过将运动输入改成连续或积分器GSTIFF换为WSTIFF来处理。其中,GSTIFF适用于大范围运动分析,WSTIFF适用于不连续度的力和运动。
(2)驱动(作用力或线性马达等)方向设置不正确。添加驱动时,如果没有选择正确的参考对象,会一直参照初始的方向,导致机构出现卡死而终止计算。
4.3.3积分器步长设置不正确
(1)最小积分器步长
在积分过程中如果模拟误差太大,积分器将减小步长(不小于积分器步长大小规定的最小值)并再次求解,直到满足所需的精度。增加最小积分器步长会减少模拟时间,但该值过大,会造成有些事件被模拟忽略而报错(…solver is stopping becausetime stepX.XXXXXXE-11 is below minimum time stepsize 1.000000E-10…)。
(2)最大积分器步长
提高最大积分器步长大小可以加速求解,减少求解模型所需的时间。但数值过大会出现以下问题:
①过大的步长易出现积分器收敛失败;
②采用默认的GSTIFF积分器时,速度和加速度存在不连续(特别是运动不顺滑或有突变);
③会错失力或运动发生突变的事件;
④无法识别实体和薄体之问存在的接触。
可采用更小的步长来避免上述问题,这样会减慢积分器的速度,但不会影响结果的精度。
4.3.4零部件之问的接触设置不正确
接触用于定义实体之间相互作用的方式,多个实体或曲线之间可以定义接触来防止穿透。通过定义接触,可以控制实体之间的摩擦和弹性属性。接触精度和接触的几何描述不正确都将导致积分器终止求解或发生相互穿透现象。可通过以下方式处理:
(1)合理选择接触的弹性属性模型,其中“冲击”适用于持续撞击,“恢复系数”适用于弹性碰撞;
(2)合理设置接触精度,通过运动算例属性中的“3D接触分辨率”调整精度大小;
(3)正确选择接触的几何描述,其中,细化几何体(3D接触)是实体的表面被划分为多个三角形的单元来简化外形描述,为默认设置,精确几何体(精确接触)采用物体表面的精确描述,占用较多计算资源。
4.3.5解算器(积分器)无法收敛
在处理带有多个冗余的复杂装配体或面时会遇到许多问题(如失稳点、快速更改运动或高速冲击等),导致解算器无法收敛,在获得结果前求解将终止。数值模拟中收敛问题是不可避免的,影响因素很多且很难预测何时会发生。解决收敛问题的基本要素如下。
(1)解算器没能取得指定的精确度。
(2)零件快速移动,雅可比验算值应设置每次迭代。
(3)机构锁定。更改初始配置或驱动重新模拟。
(4)模拟开始处终止,使用较小的初始积分器步长。
(5)使用更严格解算器,如“WSTIFF”。
(6)在模型中避免激烈断续性,如突然的运动变化、力变化或启用/禁用配合。
(7)使用速度极高的马达时,可降低马达速度。
(8)确定任何时候只有一个马达在驱动某一零部件。Motion中与收敛问题相关的参数是精确度、最大积分器步长大小,以及3D接触分辨率。如果修改上述参数无效,需检查输入是否顺滑且可微分的,带数学函数的表达式使用STEP函数优于IF语句。此外,还需检查模型缺陷和冗余约束。
4.3.6驱动的初始速度设置
初始速度设置过高,会出现报错信息(Failureto sarisfy velocity initial conditions…)。可选择重置一个较小的初始速度、增加雅可比验算数值、减小最大积分器步长大小三种方法之一来分别重新计算。
4.3.7积分器精确度
使用积分器来求解DAE运动方程,可分两个阶段得到运动方程的一个解,精确度用于控制这个解的结果精度。精确度设置的高低与积分器求解时间成反比,与计算结果的精确度成正比。默认值“0.0001”符合大多数情况,但在模拟过程中发生突然的不连续变化(如:突然改变力或马达的大小,在语句(IF、MIN、MAX、SIGN、MOD和DIM)中使用不可微的固有函数等)或系统突然发生改变时需要修改精确度值,否则积分器将终止求解。
5结束语
本文对目前运动仿真的现状进行了介绍,对SolidWorks Motion自由度的计算、解除冗余约束的方法和运动算例计算报错的原因进行了总结分析,并结合典型的四连杆机构进行了说明。得出以下结论:
(1)机构中冗余约束的判断、识别及正确移除是保证仿真顺利进行和得到精确结果数据的前提;
(2)冗余约束、精确度、最大积分器步长大小、接触分辨率、积分器类型、运动输入连续性及初始速度设置是导致运动算例计算报错的主要原因。