精益六西格玛在在线检测设备测量精度分析中的应用研究

赖涌丹

关键词：精益六西格玛;测量精度分析;测量系统分析;在线检测设备

0引言

对于具有测量功能的设备，在其新设备应用及长期的设备维保过程中，需要对其测量精度进行验证分析，以保证设备功能正常、测量结果准确有效。

以城市轨道交通机车车辆的轮对为例，其尺寸测量方式包括人工测量及机器测量。其中用于轮对尺寸的测量设备主要有传统的三维坐标测量仪及不落轮镟床（后文简称“镟床”）外，轮对尺寸在线检测设备（后文简称“在线设备”）也逐渐得到应用。

在线设备安装于正线上，现场作业条件较为复杂;且测量对象为客运列车，需保证供车率，不利于扣车进行试验。在线设备的特殊性导致其不适合设计专门的重复测量试验进行测量精度验证和分析。因此，除设备的调试验收外，在后续长期维保过程中，需对设备使用过程中产生的数据进行统计，以作为测量精度分析的依据，长期跟踪设备测量性能的变化。

本文将以轮对尺寸在线检测设备为例，对其在长期使用过程中，轮径测量精度的分析方法进行研究。

1设备测量精度分析方法现状

国内外对设备测量精度分析方法开展了大量研究。但目前的设备测量精度分析方式主要借助专门的测量试验获得一系列测量值，并对测量值与参考值信息比较，计算出测量偏差、测量偏差的平均值及极差等基础统计数据，来对设备的测量精度进行研究。而对于轮对尺寸在线检测设备的测量精度分析研究状况尚且空白。

以轮对尺寸在线检测设备为例，采用传统的方法对其运用数据进行分析。

首先收集其在2020年1-7月所获取的轮对数据，并以一定时问内该轮对在不落轮镟床（后文简称“镟床”）的测量值为参考值（镟床的测量精度需先经过试验验证，且其测量精度应高于在线设备），从而计算在线设备每次测量的测量偏差。

对上述所得测量偏差进行基础的统计，可得出以下结论：

（1）对于未经镟修的轮对，在线设备的测量偏差平均值为-0.70mm，最大达到2.66mm;

（2）对于经过镟修的轮对，在线设备的测量偏差平均值为-0.52mm，最大达到-1.36mm;

（3）由结论（1）、（2）可知，在线设备的平均测量偏差较大，测量精度不符合要求。

使用这种常规的分析方法，存在以下不足：

（1）仅能反映测量偏差的大致情况，且均值与极差易受异常值的影响，无法准确反应测量系统的问题所在;

（2）不适用于对在线设备日常使用过程中产生的测量数据进行研究;

（3）需借助专门的测量试验，不便于对设备测量精度的长期跟踪。

因此，常规的分析方法无法适应在线设备特殊的数据分析条件，需要借助精益六西格玛管理中的数据图形统计工具与测量系统分析工具进行深入研究。

2設备测量精度的六西格玛分析方法

2.1设备测量精度的分析方向

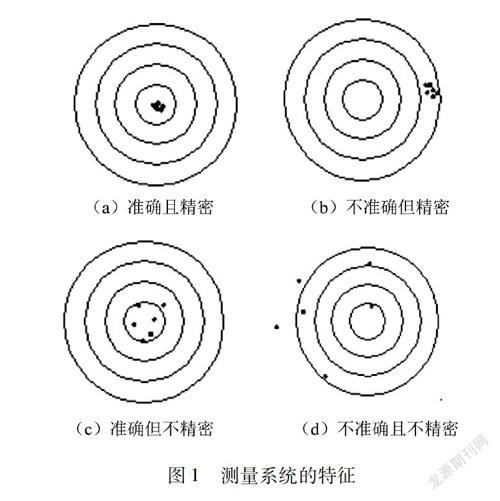
评价测量结果是否精准的两大特征为准确度和精密度，如图1所示。

准确度是指量具的测量值接近真实值的程度，表现为测量偏差的均值;精密度是指测量值彼此接近的程度，表现为测量偏差的标准差。

而在精益六西格玛管理的流程分析技术DMAIC的过程中，除了对数据的基础统计之外，测量（Measure）阶段中包含了量具R&R分析、量具的线性与偏倚分析等用于测量系统分析的工具;在分析（Analyze）阶段中也包含了分布直方图、箱线图、矩阵图、时间序列图等用于数据统计的图形分析工具。这些工具均可用于测量系统精密度、准确度的分析。

本章将结合精益六西格玛的相关工具，从测量偏差的整体分布情况、测量系统的重复性与再现性、测量系统的线性与偏倚等方面入手，对测量系统的精密度、准确度进行深入分析。测量系统研究的过程如表1所示。

2.2测量偏差的基本统计

在线设备在正常使用的过程中，每车次测量都包含有48个车轮的数据，而同一列车的两次测量相隔天数不等，因此需严格标注每组数据的测量时间，以便从横向分析其不同车轮的差异，以及从纵向分析其同个轮对随时间发生的变化。

以在线设备导出的轮对直径历史测量数据为测量值，以镟床所测得的轮对直径为参考值，根据轮对及时间的关系进行关联，并换算每次测量的测量偏差，形成本文中的试验数据样本。

按测量日期分组，对样本中的测量偏差进行基本统计，主要获取其平均值、中位数和标准差，如图2所示。从整体上看，测量偏差的均值和标准差均偏大。而中位数与均值相差较小，表明其未出现明显偏差的异常值。

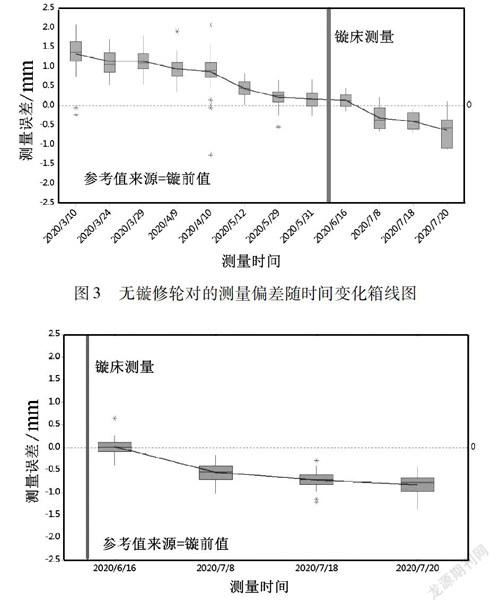
由于箱线图更能直观地反映每车次测量时各轮对测量偏差的分布情况、反映测量偏差随时间的变化情况。因此，根据不同的测量日期进行分组，绘制测量偏差的箱线图。图3～4所示分别为未镟修及已镟修轮对的箱线图。由图可知，无论轮对是否镟修，随着时间的推移均出现测量偏差逐渐往“偏小”的方向发展——即测量值越来越小于参考值，这符合实际轮径因磨耗逐渐变小的规律。

此外，对比箱线图可知，经过镟修的轮对，其测量偏差的分布范围更窄。由于轮对镟修后各处更为均匀，因此在圆周上不同点处所测得的直径值差值较小，即径向圆跳动（后文简称“圆跳动”）变小。而在线设备采用的三点定圆直径测量原理受圆跳动影响，因此镟修后的轮对测量偏差分布更为集中，符合箱线图分析结论。

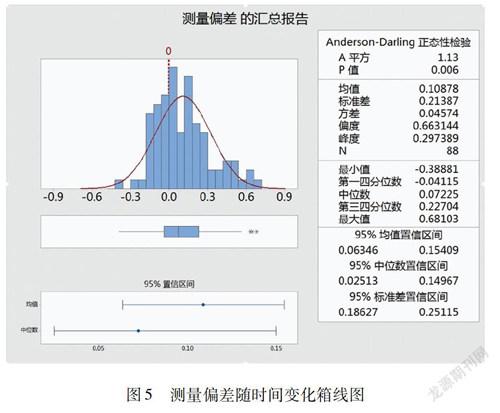
为避免轮对磨耗对数据分析带来干扰，选取最接近镟轮日期的2次测量数据为研究对象。统计得到其轮径测量偏差平均值为0.11mm，标准差为0.21mm，如图5所示。

由于基本统计所能获取的信息较少，只能对其整体表现进行评估，还需对数据进行进一步分析。

2.3测量系统的重复性及再现性

一般评定测量系统的优劣，主要从其重复性和再现性两个维度去分析。

重复性，即同一测量者使用同一测量设备在相同条件下对同组测量对象短时问内进行多次测量，其测量结果的一致性。重复性反映的是因测量设备导致的变异。

再现性，即不同测量者使用同一测量设备在相同条件下对同组测量对象短时间内进行多次测量，其测量结果的一致性。再现性反映的是因测量系统导致的变异。

由于在线设备在正常使用过程中，不会在短时问内对同一列车进行多次测量;而且其为全自动测量，其测量结果不受人为因素的影响。因此，无法严格地对其重复性及再现性进行验证。

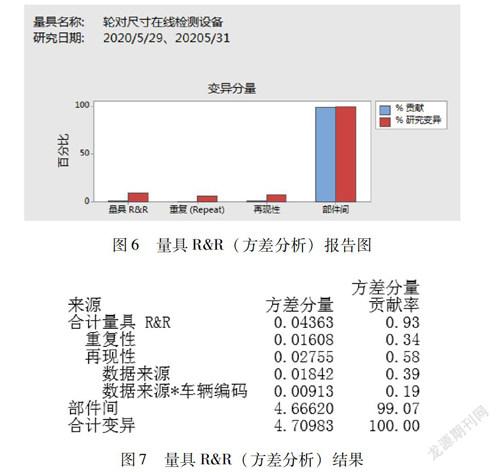
选取相隔时间较短的两次测量数据（可忽略两次测量时间所带来的附加影响时），并使用镟床测量数据作为对照数据，运用量具R&R分析对在线设备的重复性和再现性进行模糊分析，结果如图6～7所示。

得到量具R&R合计方差分量贡献率为0.93%，结合使用指导原则（表2），可知测量系统是可接受的。其中，重复性的贡献率为0.34%，由不同数据来源引起的再现性的贡献率为0.39%，表明在线设备的测量重复性、再现性良好（实质为在线设备对同一对象的重复测量精度高，且接近真值）。

而部件间差异的贡献率达99.07%，即在线设备能区分不同的轮径的轮对。

2.4测量系统的线性与偏倚

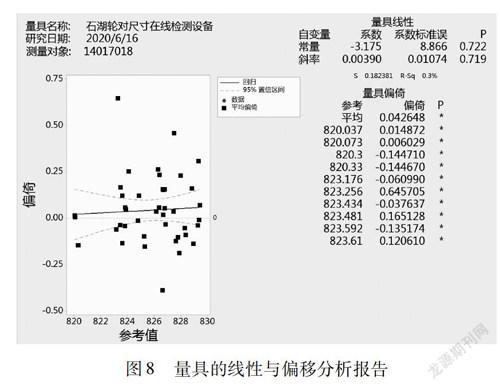
在前述分析过程中，未能体现在线设备对不同大小轮对的轮径测量结果偏移是否保持一致，因此，还需对测量系统的线性与偏移进行研究。

将每车次测量的数据作为一组，单独进行线性与偏倚研究，得到的结果如图8所示。量具线性分析结果中，常量与斜率的P=0.7（远大于0.05），因此在线设备测量系统不存在线性问题，即在不同的轮径范围下具有相同的测量准确性。

2.5测量系统的时间飘移

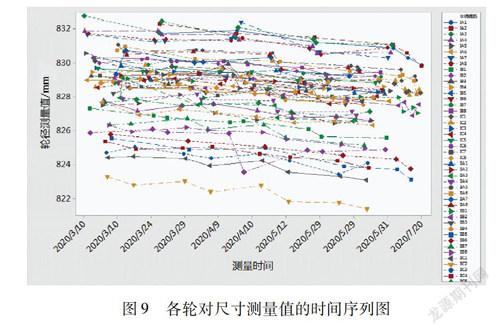
由图3可知测量偏差逐渐往负方向发展，但该变化规律可能不完全由实际轮径值的变化所引起，因此还需结合轮对的磨耗率进行综合分析，以检验测量系统是否随时间发生飘移。

对各个轮对每次测得的轮径值绘制成时间序列图，如图9所示，可见随时间推移，轮对磨耗后轮径值逐渐变小。

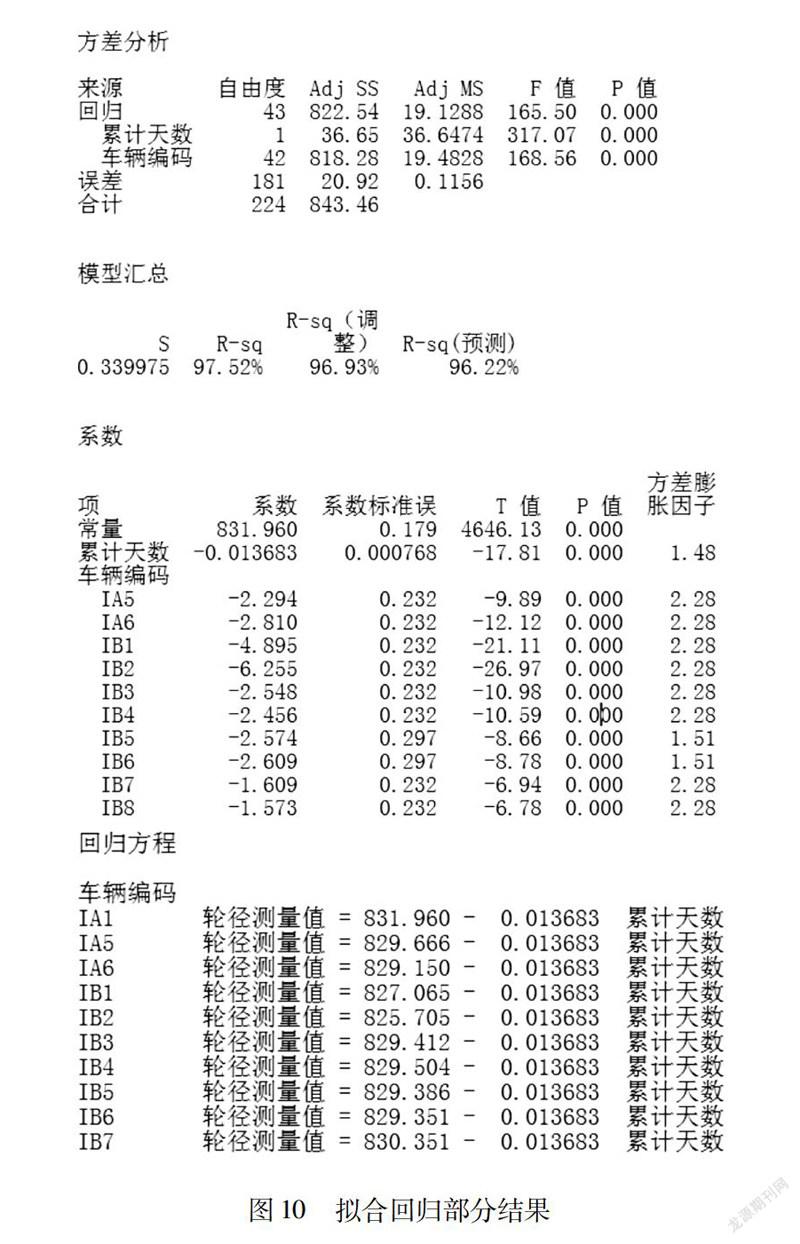
对各轮对的轮径值进行拟合回归（剔除轮对镟修的影响），图10所示为部分轮对的拟合结果，可见R-sq高达97.52%，而各轮对的拟合P值则接近于0，表明模型拟合较好。由拟合直线斜率可知轮径测量值变化率约为-0.0137 mm/天，即0.411 mm/月。

查询样本统计所在周期内，该试验车的轮径磨耗率约为0.402 mm/月。可知实际轮径磨耗率与在线设备的轮径测量值变化率近似相等，证明测量偏差随时间发生的变化为轮径磨耗所引起。即在线设备测量系统不存在随时间的测量精度飘移。

3测量精度分析总结

本文通过对在线设备测量系统的轮径测量精度在各个方面进行的一系列分析，可得到以下结论：

（1）在线设备轮径测量偏差的平均值及标准差较小;

（2）在线设备测量系统不存在线性，且重复性、再现性良好;

（3）在线设备轮径测量精度不随时间产生飘移;

（4）在線设备轮径测量精度受轮对圆跳动影响，对经过镟修的轮对的测量精度更高;

（5）在线设备能反映轮对磨耗引起的轮径变化。

由于本文所述方法是针对设备日常使用所产生的数据进行分析，受选取数据的影响，分析结论存在一定的局限性，仅适合作为设备测量精度的长期跟踪评估。若需要更为准确地评估设备测量精度，可开展专项试验，以便获取最佳实验数据进行准确分析。

4结束语

轮对尺寸在线设备使用环境特殊，开展专门的测量精度试验需要的成本和难度较大，因此需借助其日常使用过程中产生的数据来进行测量精度分析。

而传统分析方法不能全面反映测量系统的各项测量性能，且难以适应影响因子复杂的数据条件，因此需借助精益六西格玛的各种图形分析工具及测量系统分析工具进行研究。

本文以2020年3～7月轮对尺寸在线检测设备所获取的指定试验车的轮径值为例，并使用镟床测量值为标准，应用新的测量精度分析方法，对在线设备测量系统的测量精度进行了研究并得出一系列结论。证明了该分析方法的可行性和优越性。

该测量精度分析研究方法更为深入和全面，能够科学反映测量系统的性能，且能够适应复杂的数据条件，为不便于开展专项测量试验的设备的测量精度分析提供了有效的解决办法。此外，该分析研究方法还具有较高的可推广性，可应用于对其他轮对参数测量精度或其他设备的测量精度分析研究。