考虑准备时间和工件分批的柔性作业车间调度
李田丰 朱斌 张奎






关键词:柔性作业车间调度;改进遗传算法;准备时间;柔性分批
0引言
车间调度是制造系统的基础,在满足约束条件的情况下,通过优化生产性能指标,充分利用生产资源合理地安排不同种类工件的作业加工次序,以降低企业的生产成本,提高企业的竞争力。车间调度是一个复杂的问题,具有离散性、复杂性、不确定性和多约束性等特点。柔性作业车间调度问题(Flexible Job Shop Scheduling Problem,FJSP)是作业车间调度问题(Job Shop Scheduling Problem,JSP)的扩展,是更为复杂的组合优化问题。考虑准备时间和工件分批的柔性作业车间调度问题,是根据车间实际生产过程中受准备时间和工件批量影响的特点,对工件进行合理地分批,确定最优的调度方案,满足实际生产的需要。
近年来,众多学者对柔性作业车间调度问题进行了深入研究。张国辉等采用改进的遗传算法求解柔性作业车间调度问题。方水良等提出改进遗传算法,采用双链结构编码方式解决柔性车间调度问题。Singh等采用粒子群优化算法,求解考虑完工时间和延迟等多个目标的柔性作业车间调度问题。张腾飞等采用改进遗传算法,产生具有基因多样性的初始解,解决柔性作业车间调度问题。在车间实际生产过程中,工件往往成批加工,如何对工件进行分批并安排机器进行加工,已经成为急需解决的问题。对于柔性作业车间的分批调度问题,也有学者进行了研究。王云等提出一种改进的强度Pareto进化算法,用于求解柔性作业车间中分批调度多目标优化问题。陆汉东等提出一种禁忌搜索算法对分批调度中批次加工路线和子批加工顺序进行了优化。Gao等运用两阶段人工蜂群算法求解柔性作业车间分批调度问题。周亚勤等采用嵌套式遗传算法,对工件进行批量划分、加工路径确定和生产调度的综合优化。胡燕海争提出染色体两级编码的方法,用遗传算法求解柔性作业车间柔性分批调度问题。这些论文虽然对柔性作业车间分批调度问题进行了研究,但是没有考虑工件不同工序間准备时间不同的特点。
考虑准备时间和工件分批的柔性作业车间调度问题,是在满足实际生产过程中所需准备时间和工件分批的约束条件下,合理地安排加工路线,以实现最大加工时间的最小化,提高生产效率。本文以生产准备时间和工件柔性分批为约束条件,采用改进的遗传算法对柔性作业车间调度问题进行求解,最后通过对调度案例进行分析,验证了该算法可以很好地解决考虑准备时间和工件分批的柔性作业车间调度问题,能够得到最优的调度方案,使得工件的最大完工时间最小。
1柔性作业车间调度模型
1.1问题描述
柔性作业车间调度问题可描述为:有n种工件在M台机器上加工,每种工件可批量划分为若干子批,各子批次批量数随机分配;每种工件各子批次的每道工序可按照一定的工艺次序在若干台机器上进行加工,具有柔性的加工路径,各子批次工件不同工序之间需要一定的调整准备时间。工件在加工过程中应满足以下假设条件:
(1)每种工件的每道工序在可加工机器上的加工时间确定;
(2)同一时刻每台机器只能加工一道工序;
(3)同一台机器加工完同一批次的工件后再加工下一批次的工件;
(4)每道工序的生产准备时间已知;
(5)同种工件同一工序在同一台机器上加工时,不需要准备时间。
在满足以上假设条件下,以最小化最大完工时间为优化指标,制定合理的调度方案。
1.2符号定义
1.3约束和目标函数
约束1:各工件子批的每道工序只能在一台机器上加工,则有:
表1所示为一个柔性作业车间调度问题实例,有3种工件,在4台机器上加工,每种工件有20个,每个工件有3道工序,每道工序均可在多台机器上加工。
在该实例中,x为该工件的当前工序不能在对应的机器上加工;D12为工件1的第2道工序,可选择的机器集M=[M2,M4]。
2求解算法
2.1柔性分批方法
对工件进行合理的批量划分是解决柔性作业车间调度问题的关键,采用柔性分批方式对工件进行分批,可以均衡机器负荷,提高生产效率。对工件进行柔性分批时,假设各工件的子批上限为Ⅳ,各工件的子批数量和各子批的批量数随机产生。
以表1所示的调度实例为例,假设各工件的子批上限为4,分批方案如表2所示。
2.2编码
在用改进的遗传算法求解柔性作业车间调度问题时,工序排序和机器选择部分是编码的关键。本文采用双层编码的方式解决工件分批和各工件子批工序调度排序的问题,染色体由两层组成,每层染色体各由两部分组成。第一层前一部分表示工件分批编码,后一部分表示各工件子批的工序排序编码。在第二层编码中与工件分批编码对应的部分用无意义的“0”表示,机器选择部分要与第一层的工件子批工序排序部分一一对应。
以表2中第二种分批方式为例,对工序编码中的数字予以说明,如表3所示。
采用双层编码方式进行编码时,其中一条染色体如图1所示。
在图1所示的染色体编码中,3种工件的分批方案为(3,2,2)。在第一层工件子批工序调度编码中,第一次出现的6表示工件3的第1个子批的第1道工序,第二次出现的6表示工件3的第1个子批的第2道工序。在第二层机器选择编码中,工序O有3台机器可以选择,编码中的4表示在机器M4上加工。
2.3解码
染色体解码过程是将染色体转化为工件工序的调度解,主要是解决工件各子批工序排序和机器选择问题。在对染色体进行解码时,先对各工件分批编码进行解码。在对机器选择部分进行解码时,从左到右依次读取染色体的机器编码,转换为机器矩阵J、工件加工时间矩阵T1和机器准备时间矩阵T2。在对工序排序进行解码时,从左到右读取染色体的工序编码部分。同一种工件的各子批之间存在并行工序,采用间隙挤压算法计算各工件子批工序在机器上的加工时间段。解码过程中要对工件的加工结束时间与机器的空闲时间段进行比较,之后在可加工该道工序的所有机器中选择完工时间最早的机器。
2.4选择
遗传算法的每一次迭代都需要用选择算子选择出需要进行交叉或变异的个体,选择适当的个体进入下一代。选择算子有不同的性质和适应范围,由优化调度目标确定选择策略。田曼等提出的锦标赛选择方式对染色体的基因进行选择,保留种群中的最优个体。
2.5交叉
交叉是将父代染色体的基因交换组合之后产生新个体,交叉操作决定了遗传算法的性能。在双层编码中,工序分批编码的改变会引起下层机器选择编码的改变,在进行交叉操作时只需对工序分批编码进行交叉操作。刘琼等提出的IPOX交叉方法对染色体的工序编码进行交叉操作。以表1中的调度实例为例,将3种工件分为2个集合、为2个父代染色体,C1、C2为交叉产生的2个子代染色体。染色体的工序分批编码交叉操作过程如图2所示。
2.6变异
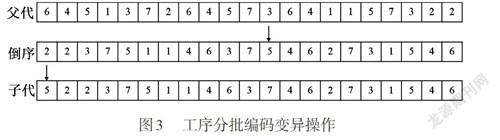
变异操作是通过随机改变染色体的某些基因以产生新的个体,增加种群的多样性。周超等提出变异方法,进行变异操作。同交叉操作一样,只需对工序分批编码进行变异操作。以图1中染色体编码为例,將染色体中的工序分批编码进行倒序排序,再将染色体中任意一个基因插到染色体最前面,可以得到子代染色体。染色体的工序分批编码变异操作如图3所示。
3调度案例
对一个4X6型柔性作业车间调度进行实例仿真,以徐本柱等提出的实例数据验证改进遗传算法的性能。该调度问题中有4种工件,在6台机器上加工,每种工件有8个,每个工件有3道工序,每道工序均可在多台机器上加工。徐本柱等采用工序并行解码算法,求得最大完工时间为83min,得到工件的最优分批方案为(1,1,4,4)。本文采用改进的遗传算法,得到的最大完工时间的最优值为79min,工件的最优分批方案为(4,1,3,4),优于徐本柱等采用的算法。采用改进的遗传算法求解时,各工件分批方案的最大完工时间如表4所示。
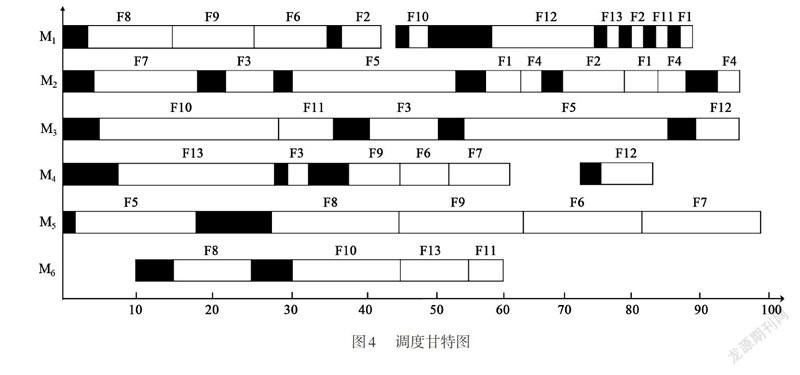
在实际加工过程中,工件在不同机器上加工时,安装、定位及刀具的更换等需要加工准备时间。在文献中4X6算例的基础上,考虑工件的加工准备时间,工件分批加工时工序的准备时间等于工序单个工件的加工时间。在考虑准备时间和工件分批的情况下,用本文改进的遗传算法求解时,求得最大完工时间的最优值为99 min,其最优分批调度方案为(4,1,4,4),第2种工件不分批,其余工件均分为4批,各批次的批量数为:(2,3,2,1)、(2,2,2,2)、(3,1,2,2)。对应调度方案的甘特图如图4所示。
在图4中,黑色部分表示工件的加工准备时间,F5为第2种工件,首次出现在机器M3上,表示第2种工件的第1道工序在机器M5上加工。F7为工件3的第2个子批,最后一道工序在机器慨上完成,完工时间为99min。
4结束语
本文对柔性作业车间调度问题进行了描述,结合实际车间生产要求,以准备时间和工件分批为约束条件,以最小化最大完工时间为优化目标,建立了考虑准备时间和工件分批的柔性作业车间调度模型。采用柔性分批的方法对工件进行批量划分,用双层编码的方式对模型进行求解,对工件的批量划分和工序调度进行了优化,提高了算法的求解效率。通过分析考虑准备时间和工件分批的柔性作业车间调度案例,得到最优的调度方案,验证了算法的可行性和有效性,能够更好地解决实际柔性作业车间调度问题。