弹性机构的动力学模型及分析
刘晓静



摘要:以梁单元作为研究基础,引入型函数与广义坐标建立单元运动微分方程。通过坐标转换矩阵与协调矩阵结合拉格朗日方程组集得到系统的运动微分方程。以弹性四杆机构作为研究对象,对其铰接点与系统内任意一点的弹性位移进行了动力学建模与分析,为后续机构的可靠性计算奠定基础。
关键词:弹性机构;动力学模型;弹性位移;运动微分方程
0 引言
早前对运动机构的研究局限于其刚性分析,对其弹性变形对工作性能及可靠性的影响考虑甚少。随着工业的不断发展,机构的弹性变形对机构的影响日益增加。现有国内外很多学者研究弹性机构的动力学分析。Howell[1]和Midha提出伪刚体模型,奠定了弹性机构的研究的基础。HETRIK[2]等研究了弹性机构的拓扑优化设计方法的重要性。张义民[3]则提出了机械动态与渐变可靠性理论。
本文以梁单元作为研究基础,引入型函数与广义坐标建立单元运动微分方程。通过坐标转换矩阵与协调矩阵结合拉格朗日方程组集得到系统的运动微分方程。以弹性四杆机构作为研究对象,对其铰接点与系统内任意一点的弹性位移进行了动力学建模与分析。
1 弹性连杆机构的模型建立
对于任意一个梁单元都可以建立一个独立的局部坐标系,取梁单元左端点作为坐标原点即可建立局部坐标系xay,如图1。
2 算例
以弹性四杆机构为例,弹性四杆机构的具体参数见表1。基于基本参数建立弹性四杆机构的动力学方程,得到系统运动微分方程,可以获得系统任意位置系统坐标系下的弹性位移。
选取连杆与曲柄的中点作为研究对象,主动杆件转速为300r/min时,选取点与对应的弹性变形示意图如图2。x1、x2为弹性轴向位移,y1、y2为弹性纵向位移。
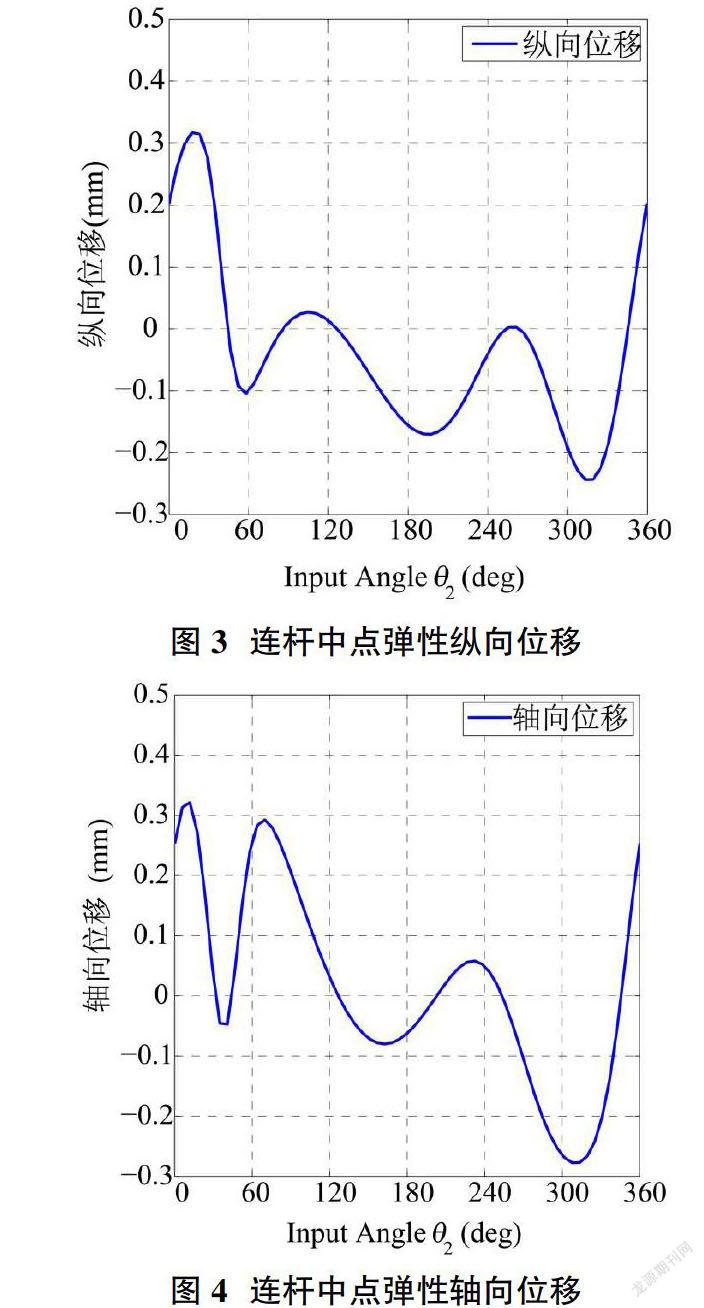
图3、图4为连杆中点的弹性轴向、纵向位移随着主动杆件转动一周的曲线图,从图3、图4中可以看出弹性变形最大值出現在0-30°,即机构启动前期,机构的启动对于连杆任意点影响较大,随着主动杆件的变化,弹性位移随之而发生波动。从图3、图4中可得到弹性连杆机构的纵向位移峰值为0.321mm,弹性纵向位移峰值为0.323mm。
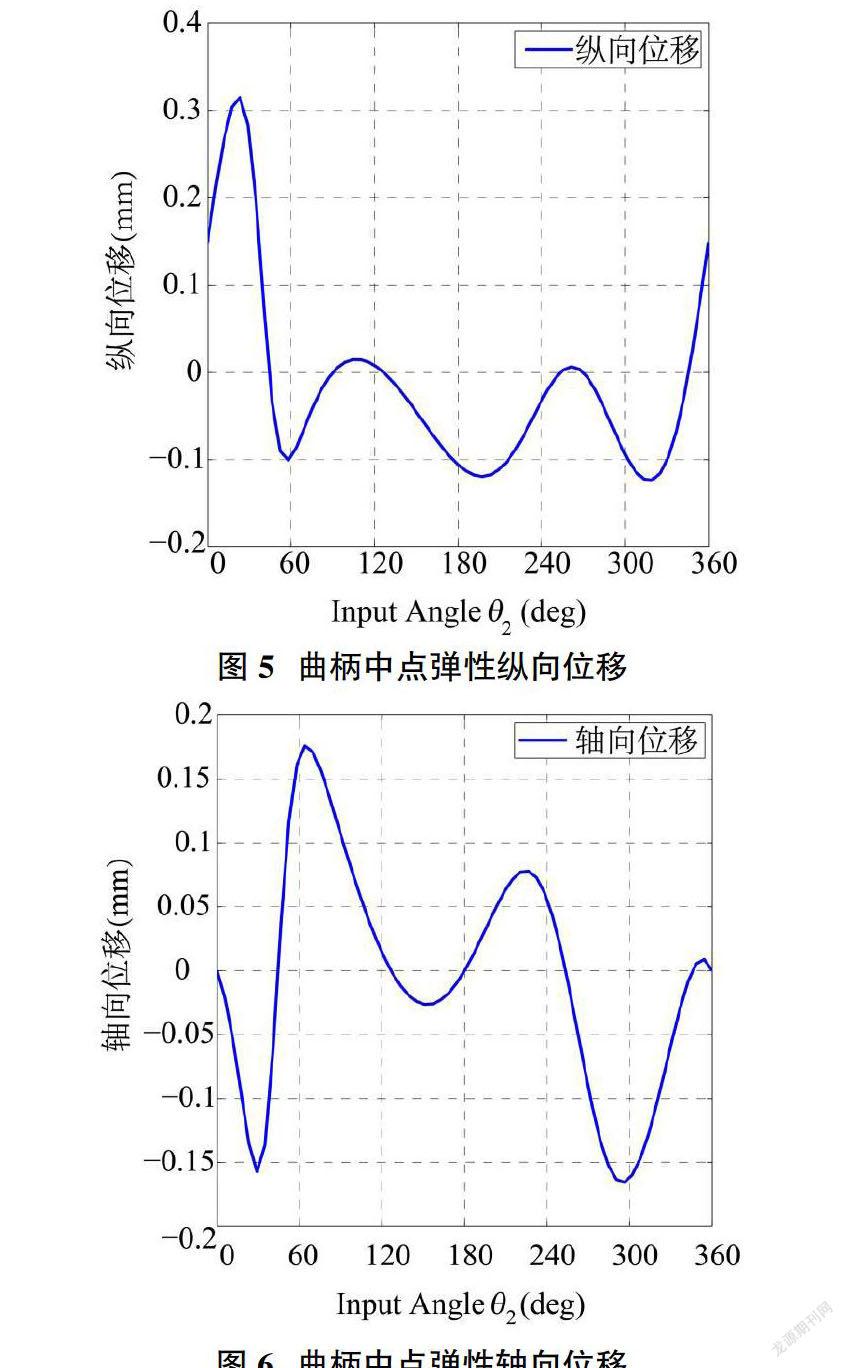
图5、图6分别为曲柄中点对应的弹性轴向、纵向位移随着主动杆件转动一周的曲线图,从图5、图6中可以得到曲柄中点的弹性变形同样最大值出现在0-30°但随着主动杆件转速变化弹性变形的波动趋势与连杆中点的变化趋势有所不同,因此杆件不同点的弹性变形在同一时刻有所不同。
3 结束语
弹性机构的弹性变形最大值出现在0-30°,即机构启动前期,机构的启动对于连杆任意点影响较大,随着主动杆件的变化,弹性位移随之而发生波动。
由此通过计算可以得到弹性四杆机构中任意一点处的弹性变形随着主动杆件转动的变形情况,为后续机构的可靠性计算打好基础。
参考文献:
[1]L. L. Howell, A.Midha, A Loop-Closure Theory for the Analysis and Synthesis of Compliant Mechanisms [J]. SME Transactions, Journal of Mechanical Design, 1996, 118(1): 121- 125.
[2]HETRIK J A,KOTA S. An energy formulation for parametric size and shape optimation of compliant mechanims[J]. Trans. ASME Journal of Mechanical Design,1999,121(3):229-233.
[3]张义民.机械动态与渐变可靠性理论与技术评述[J].机械工程学报,2013,49(20):101-114.
[4]韩清凯,孙伟,王伯平,李朝峰.机械结构有限元法基础[M].北京:科学出版社,2013:93-102.
[5]Chunmei J, Yang Q, Ling F, et al. The non-linear dynamic behavior of an elastic linkage mechanism with clearances[J]. Journal of sound and vibration, 2002, 249(2): 213-226.
[6]王小琼.弹性机构系统可靠性分析与稳健优化设计[D].东北大学,2014.

