基于alpha-beat算法的棋局研究

朱伊波 梁楠楠

【摘 要】针对点格棋博弈系统，传统搜索算法由于采用了等深度搜索，存在时间资源分配不合理，且评估函数只能依靠人工调参的问题，严重影响了算法执行效率。本课题拟采用基于α-β搜索算法的变长搜索方案，尽可能地减少在节点较多时的搜索时间，以提升搜索算法的效率;同时引入遗传算法、神经网络等算法，根据棋局状态动态调整评估函数参数，以达到提升棋力的目的。

【关键词】点格棋;α-β搜索算法;神经网络

一、引言

点格棋由于其棋型种类繁杂多变，没有定式，以及在安全边存在的情况下，估值会由于其安全边占有顺序的不同而有误差，目前，点格棋博弈系统所采用的招法确定优化方法大多都是阿尔法-贝塔（Alpha-Beta）算法，Alpha-Beta算法是对极大极小算法的优化，同时，也是一种对博弈树的剪枝策略。本项目便是针对Alpha-Beta算法进行研究。

二、基于Alpha-Beta搜索算法的变长搜索算法的操作原理

以点格棋博弈树为例，如图所示

变长搜索方案示例图

其中□代表己方拓展的节点，○代表对方拓展的节点，点格棋博弈树就是通过博弈双方轮流拓展节点来构建的。在d=4的一层节点被分成了4组，以第一组为例，节点n1的离散度为0.3小于n2，同样n3的离散度也小于n2，则只需要对n2进一步搜索。

三、变长搜索方案实现的框架构建

选取UCT搜索算法作为框架来实现该改进方案。UCT算法（上限置信区间算法）是蒙特卡洛算法的一种延伸算法，同時又将UCB算法应用到博弈树搜索上，通过UCB值的大小来选择进行评估的节点而不再是随机选择，通过UCB算法引导博弈树向更好的方向生长，有利于更快的获得最优解。UCT算法是蒙特卡洛算法当完成大量随机模拟后，不再根据模拟结果产生的胜率选择节点，因为根据UCB值更好的节点会被进行更多次的访问，所选择的节点是访问次数最多的节点。UCT算法根据模拟棋局的结果，以概率大小判断棋局盘面对己方的优劣，预估节点的好坏，优先选择表现好的节点。

UCT算法的具体流程如下：在每次选择最佳着法开始时，会建立一棵搜索树，然后依次进行如下操作：

①以当前节点为根节点开始进行搜索;

②利用UCB公式计算节点的UCB值，巧始时对节点随机赋UCB值，选择UCB值高的子节点进行搜索;

③若此子节点不是叶节点，则重复②直至搜索到叶子节点;

④检查该叶子节点是否达到规定的访问次数，如果达到规定的访问次数，则拓展该结点，该结点访问次数加1，跳到①，如果没有达到规定的访问次数跳到⑤;

⑤对弈双方均按照随机策略，轮流着子，直至棋局结束，获得模拟结果。

⑥根据模拟结果，更新博弈树结点收益值：胜利收益1，负收益0;

⑦由①开始重复，直到时间结束，或达到预设次数;

⑧由根节点的所有子节点中，选择平均收益值最高者，作为最佳节点，此节点就是UCT算法搜索的结果。

四、棋局离散度的获取

本项目采用并查集来将棋局划分为不同邻接区域，首先将棋局转换为一个只含0或1的矩阵，如果一个格子的自由度为4，就将对应的位置置0否则置1。这样就将划分邻接区域问题转化为找出该矩阵中所有相邻的1连成的区域，之后计算离散度就简单了。

五、遗传算法优化的评估函数的设计

适应度函数设计。由于经典遗传算法本身收敛速度慢，所以本项目采用适应度函数的计算方法，考虑目标函数在搜索点的变化趋势，并将目标函数的变化信息加入适应度函数指导搜索的进行，使得搜索朝着具有较大函数值变化率的方向进行;

遗传算法梯度训练。通过选择一种高效的博弈树搜索算法逐步提高博弈算法搜索的深度，逐步增强陪练算法的强度，有效的节省了训练时间;

变异和交叉操作。采用单点交叉，随机地选择染色体中的一个二进制位作为交叉点将父个体的两个参数交叉形成子个体的两个参数。

六、数据处理

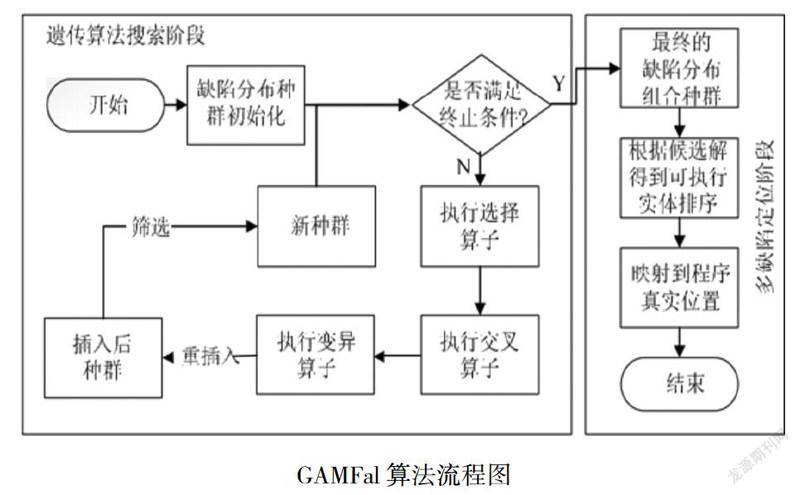
设计离散度函数、棋局评估函数、目标函数、适应度函数。同时利用GAMFal 算法。GAMFal 算法的核心是 Multi-Ochiai 可疑度系数计算公式和遗传操作算子的选择，图 2 给出了整个算法的流程图，算法共分为两个阶段，第 1 阶段首先使用贪心算法对多缺陷分布的种群进行初始化;然后执行选择、交叉和变异算子，生成新的个体并添加到种群中，同时以 Multi-Ochiai 可疑度系数作为适应度值对个体进行评价并进化得到新种群;如果终止条件被满足，则将得到最终的最优多缺陷分布种群.然后进入第 2 阶段，依据最优种群中的多缺陷分布得到对应的程序实体的可疑度排序，算法结束。

GAMFal算法流程图

七、实验方案

首先，对改进的搜索算法进行验证，实验由两程序A和B在Microsoft Visual studio 2012开发的平台下进行对弈，其中A为传统的UCT算法，B为作变长搜索改进后的UCT算法，记录两种算法在不同搜索深度下搜索到的节点数、所耗时间和胜负情况;

同样使用A、B两程序进行对弈，其中A使用的是按照自己经验设置参数的评估函数，B采用经过训练的遗传算法优化后的评估函数，双方搜索算法均采用传统的UCT算法，统计两个程序在不同搜索深度下搜到的节点数和对局的胜负情况。

使用一个贪心算法过程 Additional-Greedy（AG）来生成初始候选解种群，该算法能在满足所有个体符合条件的情况下，尽可能地保证初始种群的多样性，算法的流程图如图所示.AG 过程的输入包括覆盖矩阵 M、测试用例结果向量 R 以及遗传算法种群中包含的个体数量 Np.AG 过程首先生成 n 个个体，每一个个体（即候选缺陷分布）均只有一条语句被认为有错，即长度为 n 的二进制串中只有一个位置为1，其他为 0，且个体之间 1 的位置互异，如图所示.计算每一个个体的（C）值，如果（C）=|TF|，则该候选缺陷分布C能够解释所有的失败测试用例，是本问题的一个可行解.如果（C）>|TF|，则需要对该个体进行修正，即在该候选缺陷分布中加入语句 ex（即把缺陷分布组合中 ex 对应的位置置 1），使得该候选缺陷分布能够解释所有的失败的测试用例.ex 需要能够解释最多的原候选缺陷分布不能解释的失败测试用例;也就是说，在 ex 被加入到候选缺陷分布 C 后，（C）增加的幅度最大;ex 加入后，C 如果能够解释所有的失败测试用例，则该过程结束，若不能，则继续加入语句，直到该个体能够解释所有失败测试用例为止.至此，AG 过程获得了一个有 n 个可行个体的种群.如果 n Np，则复制数个可行个体直至将初始种群中个体数量补充至 Np;如果 n Np，则选择其中 Multi-Ochiai 可疑度值最大，即适应度值最高的 Np 个个体作为初始种群.AG 过程生成的 Np 个个体的初始种群具有相对较高的适应度值，且具有较好的多样性，因为每个个体都是由具有不同缺陷位置的候选缺陷分布扩展而来.高质量的初始种群有利于遗传算法最终得到较好的结果. 初始化得到的种群将依次使用选择、交叉和变异算子来产生新的个体.新个体再重插入到种群中，开始新一轮的选择、交叉和变异。

AG过程流程图

八、结语

点格棋未来将会优化出更加先进的计算方式，但当下α-β算法仍是主流方式。本文对α-β算法提出一种优化，希望为来点格棋算法会更加先进。

【参考文献】

[1]刘洋，点格棋博弈中UCT算法的研究与实现[D]，合肥，安徽大学，2018.

[2]李学俊，王小龙，吴蕾，等.六子棋中基于局部“路"扫描方式的博弈树生成算法[J].智能系统学报，2015（2）：267一272.

[3]唐霜霜，点格棋机器博弈系统的研宄与实现[ D]，合肥：安徽大学，2015，

[4]刘淑英，穆远彪，李红·基于alpha-beta剪枝搜索算法的中国象棋游戏设计[J].信息通信，2015（8）：47一48.

[5]陈业鹏·基于Alpha-Beta搜索算法的中国象棋人机对战的设计与实现[J ]、计算机光盘软件与应用，2012（4）197一199.