体验数学建模完整过程 发展数学学科核心素养
王保东
摘 要:执教教师基于对教学内容和学情的分析,准确设置目标,恰当处理课内、外探究活动,将信息技术与课堂教学深度融合,指导学生全员全程体验数学建模的完整过程,积累了数学建模的经验,在数学建模过程中引导学生用数学眼光观察世界、用数学思维思考世界、用数学语言表达世界,提升了学生的数学学科核心素养.
关键词:数学建模活动;课内外探究;技术深度融合
“数学建模活动——茶水最佳饮用时间”是人教A版《普通高中教科书·数学(必修)》第一册中新增加的数学建模活动内容,是落实“四基”“四能”的良好素材. 执教教师以“单元—课时”教学设计方式展示自己对数学、学生、教学和技术的理解,对《普通高中数学课程标准(2017年版)》(以下简称《标准》)的要求把握准确,对教学内容的理解和学情分析恰当,教学活动设计与实施合理,引领学生体验数学建模活动的完整过程,积累了数学建模的经验. 学生在用数学眼光观察世界、用数学思维思考世界、用数学语言表达世界的过程中体会了数学建模的意义和数学的应用价值,发展了数学学科核心素养.
一、正确理解内容,把握教学重点
《标准》给出了数学建模活动的课程要求与定位:数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养. 数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题. 数学建模活动是高中阶段数学教学的四大主线内容之一,是基于数学思维运用模型解决实际问题的一类综合实践活动,是综合提升数学学科核心素养的有效载体.
数学建模活动的教学要以課题研究的形式开展,课题研究的过程包括选题、开题、做题、结题四个环节.
“建立函数模型解决实际问题”是“数学建模活动与数学探究活动”的第一课时,是高中数学教学的难点之一. 学生在本节课积累的研究经验对后面数学建模活动的开展具有奠基作用.“茶水最佳饮用时间”的探究是学生以具体实例的方式体验选题和做题两个环节,是本节课的主要内容.
执教教师基于对教学内容的理解确定了教学重点:函数模型的建立、检验与优化. 师生把主要精力放在了相关内容的探究上,突出了教学重点.
二、目标定位准确,叙述科学合理
《标准》的教学建议指出,教学目标的制定要突出数学学科核心素养,要引导学生理解基础知识、掌握基本技能、感悟数学基本思想、积累数学基本活动经验. 这与章建跃博士主张的“落实‘四基’‘四能’就是落实数学核心素养”是一脉相承的.
在本节课的教学目标设计中,执教教师首先以《标准》的要求为依据,从积累活动经验、提高能力、发展素养和体会数学建模活动价值的角度给出一般要求,然后从课时目标的角度将单元目标分解,具体化为学生学习后的行为表现,正确处理了单元目标和课时目标之间的关系.
特别是在课时目标的设计上,各个目标都指向学生的学习结果,具有具体、可操作和可检测的特点. 如“能对现实问题进行数学抽象,准确收集数据”等,说明学生是学习的主体已经根植于教师心中,并外显为一种教学习惯. 另外,在课时目标的设计中,既有具体知识和方法的获得,也有思想、方法和能力的具体要求,体现了显性目标和隐性目标的相互融合.
三、学情分析准确,应对策略得当
执教教师从学生求解应用题的经验、高中预备知识与函数主题的学习中积累的知识、方法、能力、素养等方面分析了学生已有的认知基础,从开展数学建模活动对学生将实际问题抽象为数学问题、收集数据、分析数据、建立模型、求解和检验模型等环节需要的能力方面分析了达成教学目标所需具备的认知基础,并分析了“已有的基础”与“需要的基础”之间的差异,确定了本节课的教学难点:函数模型的检验和优化.
结合学情分析,预设了突破教学难点的策略:采用核心任务探究的教学方式,每个核心任务下设子任务,借助信息技术直观作图、数据分析等功能,通过独立思考、小组合作、展示交流、质疑追问、互评反思等师生活动来强化教学重点、突破教学难点.
四、全员全程体验,科研氛围浓厚
执教教师组织学生运用小组合作的方式,合理安排课内、外探究活动,做到全员全程完整体验建模过程,让学生感受教学过程中的科研氛围.
在课外探究活动中,执教教师提前布置了三个任务. 第一,进入茶坊调研影响茶水口感的因素有哪些,主要因素是什么,利用文献检索调查茶水最佳口感温度;第二,利用计算机、数据采集器、温度传感器收集茶水温度随时间变化的数据;第三,梳理已学函数的定义、图象和性质,形成思维导图. 这些课外探究活动的顺利完成,既显示出团队合作的威力,又有利于学生发挥特长,还可以减轻课堂教学时间紧张的压力.
在课内探究中,执教教师先播放采茶、制茶、品茶的视频创设实际情境,引出饮茶最佳口感问题. 然后,让学生代表分别对影响茶水口感的因素、茶水最佳口感温度的调研结果进行汇报. 最后,执教教师采用前后一致、逻辑连贯的3个问题串和及时追问将探究任务有机融合.
问题1是“刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感呢?从数学的角度看,需要研究什么问题”. 在学生回答“茶水温度随时间变化的规律”后,教师继续追问“怎样才能找到这种规律呢”,学生在教师的引领下体会用数学眼光观察世界、借助函数语言表达世界,提高数学抽象能力.
问题2是“你能表述一下你的研究方案吗”,并及时追问“我们首先需要做些什么”,在学生回答“先收集数据”后,由学生代表汇报课外探究时收集的数据,并建议随机选择一组数据作为研究对象. 之后进一步提问:怎样才能够更加直观地看出茶水温度随时间变化的规律?怎样用准确的数学语言来刻画这种规律?散点图契合哪种函数图象?学生在教师的引领下体会借助图象直观地分析数据特点,推测函数的类别和相应解析式,提高了直观想象和数据分析的能力.
问题3是让小组合作选择一种函数模型,给出拟合曲线和解析式,并对函数模型进行评价,小组代表汇报. 在学生代表对自己汇报的函数模型表现出不满意后,追问:谁能帮助这个小组回答这个问题?在学生建议应考虑具体函数定义域时,继续追问:可以对函数模型做出哪些改动?引领学生由利用幂型函数、指数型函数模型刻画变化规律转化为由幂型函数、指数函数简单复合后形成的新的函数模型刻画变化规律,并重构和检验了函数模型,进而解决实际问题,提高了学生的逻辑推理能力.
从教学过程来看,执教教师思路清晰,对问题的设计和处理符合学生的认知基础及知识生成的逻辑顺序,师生互动高效,教学效果好.
五、深度融合技术,运用适时适度
本节课的实施过程,体现了信息技术使用的适切性,突出了信息技术與数学课程的深度融合. 具备如下亮点.
1. 信息技术手段多样
本节课的信息技术手段包括计算机、数据采集器、温度传感器、室温计、平板电脑、手机(或相机)、GeoGebra软件和MATLAB软件等.
2. 信息技术运用节点优势明显
教师指导学生运用计算机、数据采集器、温度传感器、室温计等测量工具收集数据,保证了方法的科学和数据的准确;用GeoGebra软件,操作简单、图象直观,统计结果清晰明了且全面,保证了数据处理的高效快捷;用MATLAB软件解决解析式中有限制条件的函数拟合和检验问题,显示了软件的独特功能;教师利用平板电脑拍摄的图像清晰,及时反馈典型探究案例,便于互动交流,发展学生理性思维.
3. 信息技术手段运用娴熟
师生技术手段运用娴熟,为高效率处理数据、分析检验模型奠定了基础.
六、教学思考
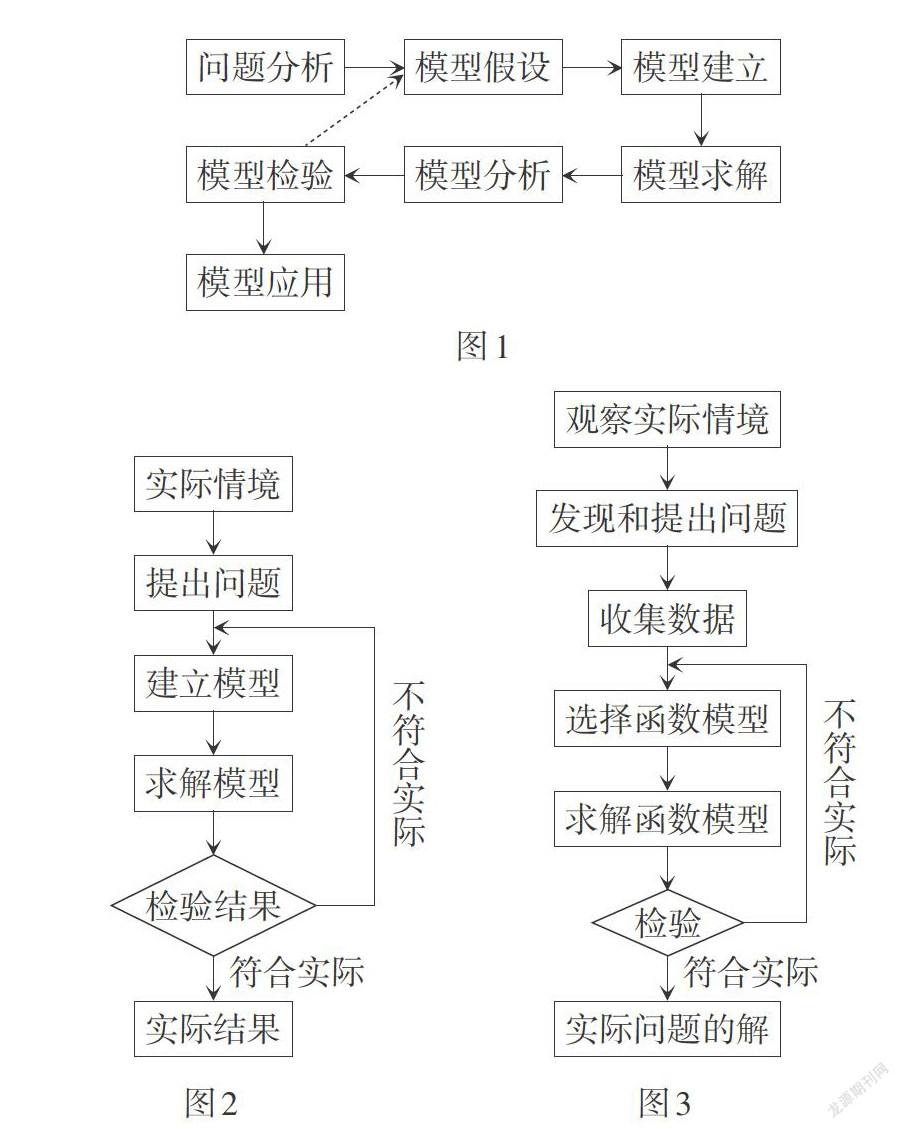
执教教师在本节课的课堂小结中给出了数学建模的一般步骤(如图1),这与《标准》中数学建模的一般步骤(如图2)、教材或教师参考用书中的研究步骤(如图3)略有不同.
事实上,图1和图2给出的是数学建模的一般步骤,图3给出的是建立函数模型解决实际问题的一般步骤. 根据本节课的教学安排,建议采用建构函数模型解决实际问题的一般步骤,并增加观察实际情境的环节,让学生体会在各个环节中研究问题的普适性方法和策略.
参考文献:
[1]中华人民共和国教育部制定. 普通高中数学课程标准(2017年版)[M]. 北京:人民教育出版社,2018.
[2]章建跃,张艳娇,金克勤. 数学建模活动的课程理解、教材设计与教学实施[J]. 中学数学教学参考(上旬),2020(5):13-19.
[3]章建跃,张艳娇,金克勤. 数学建模活动的课程理解、教材设计与教学实施(续)[J]. 中学数学教学参考(上旬),2020(6):13-16,31.

