使用径向电阻率比值计算Sw的方法研究

杨克兵，蔡建国，谢 力，赵 克，祖 满，陈利平

(1.中国石油华北油田公司 塔里木项目部,河北 任丘 062552； 2.中国石油华北油田公司 采油一厂，河北 任丘 062552)

储层含油饱和度是油气层定量评价和储量计算的关键参数，但早期油气勘探并没有合适的方法求取，直到1942年阿尔奇提出使用电阻率、孔隙度评价储层含水饱和度的公式后[1]，才建立了一套储层含油气饱和度的定量评价技术，实现了储层含水饱和度的计算。实际应用表明，在泥质、低孔隙、低阻储层使用效果不是太好。针对这些问题，研究人员依据地质条件修正阿尔奇公式，派生出各种各样的引申公式来提高含水饱和度的计算精度[2-5]。即使这样，也没有完全解决问题。当前，尽管有核磁测井可以提供精度较高的含水饱和度资料，但由于价格较贵，无法普遍应用，储量评价参数主要来自常规测井资料的解释，研究人员仍然在为提高含水饱和度计算精度而努力。如Verga等(2001)深入研究了使用测井资料确定含水饱和度的不确定性[6]，Melani等(2015)讨论了阿尔奇参数对碳酸盐岩储层含水饱和度计算的影响[7]，Sarihi等(2015)提升了受粘土矿物导电性影响的致密储层含水饱和度计算精度[8]，Yu等(2018)优选了页岩气层含水饱和度的计算方法并进行改进[9]。因此，可靠的含水饱和度计算方法仍需要进一步探索。

在计算储层含水饱和度的所有方法中，径向电阻率比值法可谓独树一帜，一直在不断发展进步。其核心是用同一测量深度点的不同径向探测深度的电阻率值进行比较，进而评价储层的含油性。这一方法在二十世纪90年代初就开展应用研究，见到明显效果。如1990年王协生提出了一种径向电阻率求含水饱和度的方法[10]，随后这一方法被申本科(1996)应用到水淹层的解释评价上[11]。后来，使用径向电阻率比值评价油水层的方法发展到测井交会图技术上。如丁娱娇等(2009)用径向电阻率比值交会图评价复杂油气藏[12]，李功强等(2010)评价低孔、低渗储层[13]，侯科锋等(2017)进行气水层评价[14]，黄若坤等(2017)进行沥青砂岩储层评价[15]。同时，计算含水饱和度的方法也得到发展，如杨克兵等(2015)提出了依据径向电阻率比值计算储层视含水饱和度的方法[16-17]，赵璐阳等(2018)把该方法用于苏里格低阻气层评价[18]，也取得了较好的效果。同时，该方法已由杨克兵等于2016年获国家发明专利[19]。但是，上述方法还不够完善。首先，并没有从原理上论证径向电阻率比值法评价储层含油性的依据，即径向电阻率比值是否能够反映储层的含油性问题；其次，所提出的含水饱和度计算公式要么操作复杂，无法推广使用[10-11]。要么过于简单，计算精度可能达不到使用要求[17]。由于径向电阻率比值法理论上能够评价低阻油气层，能够弥补当前油气水层评价方法的不足。因此，继续深入研究径向电阻率比值法计算含水饱和度的方法，必将有助于解决低阻油层、复杂油气层等当前测井疑难层的识别评价问题，有助于提高测井解释符合率，为推动相关领域测井技术发展提供依据。

1 径向电阻率比值评价油水层的一般原理

电阻率曲线是计算含水饱和度的最关键资料，与自然伽马、中子等测井曲线不同的是，电阻率测井有不同径向探测深度的曲线，如感应电阻率测井有深、中、浅3条曲线，阵列感应电阻率曲线有不同径向探测深度的5条或6条曲线。还有不同设计原理的测井仪器，如双侧向测井系列与感应测井系列等，这就为使用径向电阻率比值评价油水层提供了依据[20]。

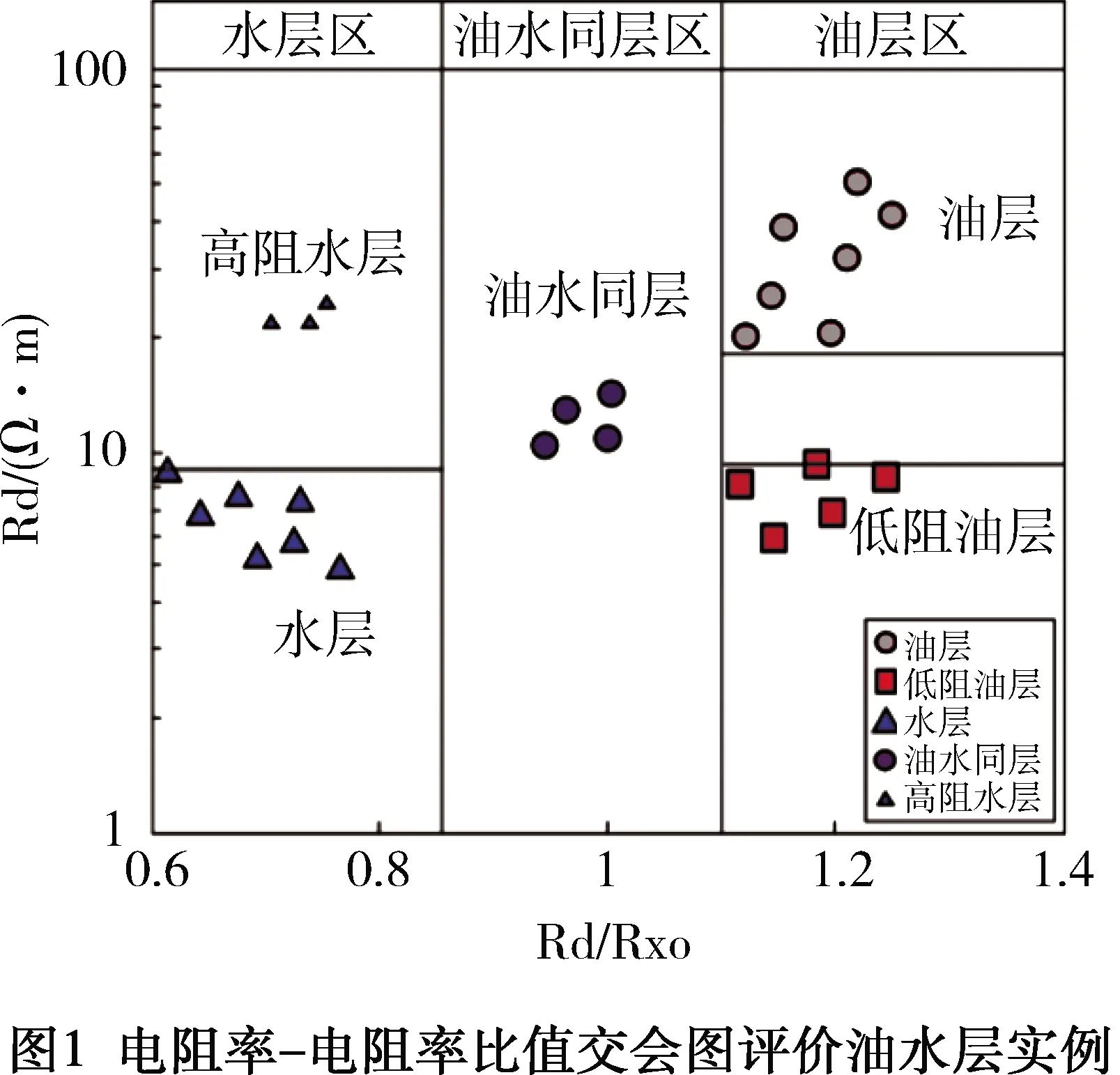
如果径向电阻率比值能够反映储层的含油性，则可用交会图版和含水饱和度计算等方法实现对油水层的评价。例如使用径向电阻率比值制作交会图版，就可把油层、低阻油层、油水层、高阻水层在一张交会图上明显区分开(见图1)，这是目前其它测井交会图技术无法实现的，完美展现了径向电阻率比值评价低阻油气层的优势。

例如依据径向电阻率比值用公式计算储层含水饱和度，最简单的方法用类比法就可实现。其原理是用水层径向电阻率比值作为尺子来刻度未知层的含水饱和度，从而计算储层含水饱和度。假定含水饱和度为100%的纯水层其原状地层电阻率与地层冲洗带电阻率的比值为常数a，即a=Ro/Rxo，未知含水饱和度储层其原状地层电阻率与地层冲洗带电阻率的比值为b，即b=Rt/Rxo，如果储层径向电阻率比值是储层含油气程度的反映，则a与b的比值可定义为储层含水程度。因为a是储层100%含水程度的反映，而b是储层含水程度不同时的反映，当储层为纯水层时，b≈a。实际资料表明，当储层含油性越高时b值越大，越低时b值越小，直到与纯水层相当。纯水层含水程度100%，纯油层含水程度可能接近0，与阿尔奇公式计算的含水饱和度Sw值的特点有相似性，可看作是一种视含水饱和度[17]。

可以看出，在原理上使用径向电阻率比值能够较容易的实现对油气水层的评价，其关键是径向电阻率比值能否反映储层的含油性问题。但是，当前研究人员一般认为径向电阻率值受泥浆滤液侵入或岩性变化等影响较大，淡水、咸水泥浆钻井剖面径向电阻率比值对储层含油性的反映特征可能存在不一致现象，并没有去深入研究这个问题。因而导致使用径向电阻率比值评价油水层的这一方法推广应用成效并不显著，依靠径向电阻率比值法评价低阻油气层的方法并没有引起当前测井界的重视，还没有获得广泛认同。实际上，排除电阻率测井资料的质量问题后，使用径向电阻率的侵入特征进行油水层评价是一种测井解释基础方法。大量的实例证实了这一方法的可靠性，表明径向电阻率比值与储层的含油性存在密切关系，只是缺乏进一步的深入研究。

新的研究表明，径向电阻率比值与储层的含水饱和度为幂函数关系，证实径向电阻率比值与储层含油性存在一一对应关系，能够反映储层的含油性，为使用径向电阻率比值评价油水层提供了理论依据。

2 储层含水饱和度Sw的计算公式

本次研究，以阿尔奇公式为理论依据，结合地层侵入模型，推导最广泛条件下的径向电阻率比值储层含水饱和度计算公式，并进行实验验证。详细过程如下：

2.1 公式推导

根据阿尔奇公式，储层深电阻率与完全侵入状态下冲洗带电阻率可表示为[21-22]：

(1)

(2)

可推出：

(3)

对于完全侵入的冲洗带地层，Sxo=1，则式(3)可变为:

(4)

可推出：

(5)

上式即为使用电阻率比值计算储层含水饱和度的新公式。

式(1)至式(5)中：Rt、Rxo—储层同一个测量点深、冲洗带电阻率测井值，Ω·m；Rw—原状地层水电阻率，Ω·m；Rmf—泥浆滤液电阻率，Ω·m；a、b、m、n—岩电参数，小数；Sw、Sxo—储层及冲洗带含水饱和度，小数。

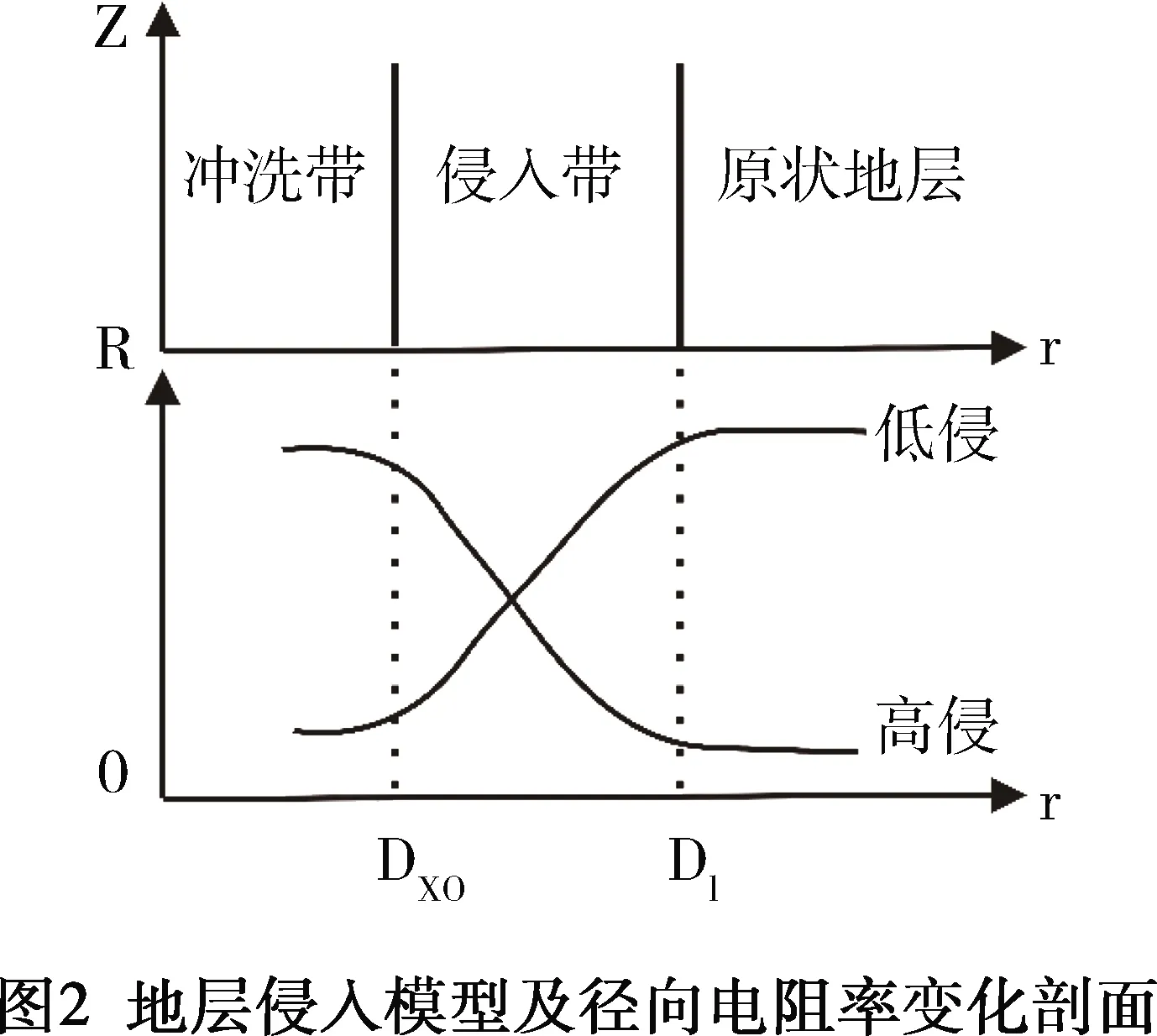
上述推导成立有一个重要前提条件，就是冲洗带含水饱和度为1，即冲洗带被完全侵入。冲洗带是指由于井筒内泥浆的侵入作用，地层中可动流体完全被泥浆滤液驱替后形成的一个绕井筒的环状条带，径向深度10 cm左右。根据地层侵入模型，泥浆滤液侵入油、气、水层可划分为三段式模型(见图2)。靠近井壁的第一段，即冲洗带，泥浆滤液侵入程度最高，基本认为是完全侵入。第二段，泥浆滤液侵入与原状地层流体交互，是泥浆滤液侵入能够影响的区域，叫做侵入带或过渡带。第三段，泥浆滤液侵入无法影响到的区域，即原状地层带[23-24]。因此，针对实际钻井情况，油、气、水层冲洗带被完全侵入是绝大多数情况，表明冲洗带含水饱和度为1这一假设在计算中是可行的。

可以看出，在新公式中只有三个参数Rw、Rmf、n，这三个参数均为常数项，这就表明储层含水饱和度与深电阻率和冲洗带电阻率比值为幂函数关系，说明储层的含油性与深电阻率和冲洗带电阻率比值正相关。当含水饱和度值最大时，径向电阻率比值最小；当含水饱和度值变小时，径向电阻率比值随着变大。即不管是淡水泥浆还是咸水泥浆钻井，径向电阻率比值对储层含油性的反映具有相同的特征，径向电阻率比值越大，储层的含油性越好，径向电阻率比值越小，储层的含油性越差。这是本研究的一个新认识，打破了以前淡水泥浆和咸水泥浆钻井径向电阻率比值对含油性的反映存在不一致的传统认识。因此，在冲洗带完全侵入时，深电阻率和冲洗带电阻率比值能够反映储层的含油性。

2.2 实验数据的验证

利用多块岩心进行实验来检验含水饱和度计算公式的可靠性，首先用3 000 mg/L的盐水浸泡岩心，模拟完全侵入的冲洗带泥浆滤液电阻率，测量含水饱和度为100%时的岩心电阻率，作为储层冲洗带电阻率；其次，用8 000 mg/L的盐水浸泡岩心，模拟原状地层水电阻率，再用煤油进行驱替，记录不同驱替程度时测量得到岩心电阻率及含水饱和度，作为原状地层水条件下不同含水程度的储层真电阻率。根据所提出的含水饱和度新公式(5)进行储层含水饱和度计算，计算结果与测量值的对比见表1。

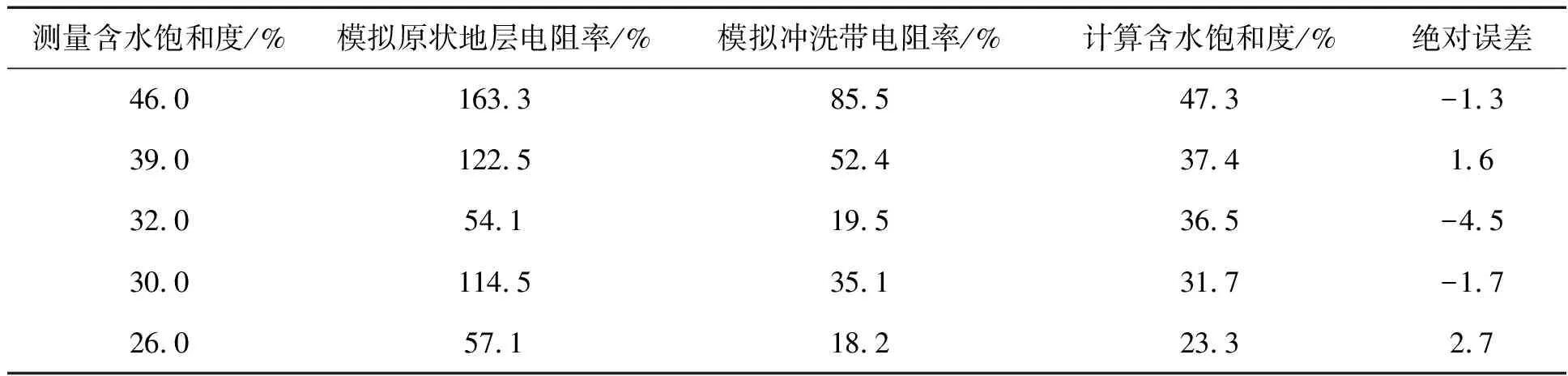
表1 岩心实验与储层含水饱和度计算结果对比

可以看出，利用(5)式计算的含水饱和度与实际岩心测量的含水饱和度最大绝对误差为4.5%，最小绝对误差为1.3%，平均绝对误差为2.4%，其精度达到了测井计算含水饱和度的行业要求。因此，当公式需要参数n、Rw/Rmf能够有效确定时，用新公式(5)计算的储层含水饱和度能够在生产实际中使用。

3 参数的获取及应用实例

3.1 参数的获取

公式中共有三个参数Rw、Rmf、n需要确定，其中，Rw、Rmf只需要比值Rw/Rmf即可，并不需要其具体值。当然，有Rw、Rmf的具体值更好，其效果与获取比值Rw/Rmf是一样的。可以看出，实际应用中只需要确定两个参数，即Rw/Rmf值与n值。

3.1.1 参数Rw/Rmf的获取

参数Rw/Rmf值获取的方法较多，如可用自然电位相对幅度公式获取，可用泥浆电阻率和泥浆滤液电阻率之间的经验公式获取[23-24]，还可用纯水层径向电阻率比值获取。综合来说，使用完全侵入纯水层径向电阻率比值确定的方法效果最好[17]，能够给出较为可靠的地层水电阻率与泥浆滤液电阻率的比值。

在地层完全侵入条件下，邻近水层的径向电阻率比值正好等于地层水电阻率和泥浆电阻率的比值，这一规律可由阿尔奇公式推导证明。

依据阿尔奇公式，完全侵入的纯水层径向电阻率测井响应方程为：

(6)

(7)

可推出：

(8)

式中：Ro、Rxo—纯水层径向电阻率测井值，Ω·m；Rw—原状地层水电阻率，Ω·m；Rmf—泥浆滤液电阻率，Ω·m；a、b、m—岩性系数、孔隙度指数。

可以看出，对完全侵入的纯水层，其深探测电阻率与冲洗带探测电阻率的比值理论上为一常数，即原状地层水电阻率与泥浆滤液电阻率的比值Rw/Rmf。由于沉积原因，在一个油水系统下，地层原状地层水电阻率Rw的值是基本稳定的，对于同一口井，钻井泥浆滤液电阻率也基本稳定，因此，其比值也是稳定的，是基本接近的常数。通过对实际测井资料考察，纯水层径向电阻率曲线的比值变化不大，基本为一常数，由于计算的需要，取其中最小者作为计算参数。

3.1.2 参数n的获取

参数n就是饱和度指数，一般可从岩电实验资料获取。由于当前所有老油田区块均开展过岩电实验研究，因此参数n可直接使用岩电实验测量资料。在没有岩电实验资料的勘探新区，可采用区域经验参数进行计算。同时，前人对饱和度指数n的影响因素进行了大量研究，认为饱和度指数主要与储层地层水矿化度、孔隙度、渗透率、孔隙结构等相关，提出了一些饱和度指数确定方法[25-28]。如用地层水电阻率与饱和度指数回归等，也可采用这些方法得到饱和度指数n。

3.2 有岩心资料井的应用实例

图3是某区块有岩心测量含水饱和度资料井处理实例(XX6-5井)，所用含水饱和度资料为压汞实验束缚水饱和度资料，能够代表储层饱含油气时的理想含水饱和度。电阻率资料为阵列感应，用R9代表原状地层电阻率，R1代表完全侵入冲洗带电阻率，根据下部典型水层R9/R1值确定Rw/Rmf值，用岩电实验资料确定n值。采用新公式对该井进行处理，可以看出，目的层段2230-2270所计算含水饱和度与实验测量束缚水饱和度变化趋势基本一致，所计算含水饱和度最高49.2%，最低29.6%，符合油气层标准。本层试油，日产油17.1 m3，日产气26.28万m3，日产水少量，为一凝析气层，处理结果与试油结论吻合。从所计算含水饱和度与束缚水饱和度的对比看，最大绝对误差为13.8%，最小绝对误差为0.1%，平均绝对误差为3.55%，其精度能够满足使用要求。

此外，使用新公式进行含水饱和度计算，由于使用纯水层的径向电阻率比值对计算结果进行标定，使得计算含水饱和度比较合理，没有大于100%的情况，避免了使用阿尔奇公式因参数选取不当而导致Sw>100%的情况[29-30]。同时，对差油层、干层等物性差的复杂孔隙储层，由于与油层采用相同的处理参数，也避免了参数取值误差导致的计算不合理问题, 提高了含水饱和度的计算精度。

4 结论

1)通过对径向电阻率比值使用阿尔奇公式进行分析，所推导出的储层含水饱和度计算公式理论基础扎实，这一公式是可靠的，为储层含水饱和度计算提供了一种新的有效方法。

2)新公式进一步完善和发展了对储层含油性的评价，提出了多个新认识。一是径向电阻率比值与储层含水饱和度为幂函数关系，反映了岩电关系的本质。二是径向电阻率比值无论淡水泥浆还是咸水泥浆钻井，对储层含油性反映是一致的，为使用交会图等多种方法评价油气层提供了依据。它表明储层的含油性与深电阻率的绝对高低没有必然关系，而与储层的径向电阻率比值相关，摆脱了传统高阻是油、低阻是水的解释模式，为常规测井资料评价低阻油层、复杂孔隙油层、水淹层等提供了一个新的方法。

3)经过岩心试验资料检验和单井数字处理验证，新公式的计算结果能够满足测井行业的使用要求，避免了阿尔奇公式因参数取值误差导致的计算不合理问题，有助于提高测井解释符合率，值得进一步推广使用。