含圆弧形缓冲结构的仿袋鼠腿悬架建模与行为特性研究

宋勇,刘林鑫,李占龙,连晋毅,孟杰,燕碧娟

(太原科技大学机械工程学院,030024,太原)

悬架是车辆车架(车身)和车桥(车轮)之间一切传力连接装置的总称。它弹性地连接车身和车桥,缓冲和传递不平路面产生的振动与冲击,确保车辆具有一定的乘坐舒适性和操纵稳定性[1-3]。因此,车辆的品质在一定程度上取决于悬架的结构与性能。悬架一般由弹性元件、减振元件和导向机构共3部分组成。按刚度、阻尼参数是否可调节分为被动悬架、半主动悬架和主动悬架。被动悬架因成本低、可靠性高、技术较成熟等优点,现已被广泛应用,但因刚度、阻尼参数不可调节,难以确保车辆在不同工况下的乘坐舒适性和操纵稳定性。随着车辆的广泛应用以及人们对车辆舒适性和安全性要求的日益严格,悬架的结构与性能设计面临着严峻的挑战。因此,设计与研究一种舒适、安全的高品质悬架已成为当前车辆研发的一个重要课题。

仿生学是一门交叉学科,为解决复杂、困难的工程问题提供了新思路和新方法[4-7]。研究发现,生活在澳大利亚草原和沙漠等复杂地形中的袋鼠,其腿部结构通过不断的进化演变,形成了独特的运动结构,具有合理的肌肉、尺寸比例和质量分布,拥有奔跑速度快、越障碍能力强、运动稳健且能耗低等特点[8-10]。这些特点与车辆悬架的特性要求不谋而合。受此启发,文献[11-12]借鉴长期进化的袋鼠腿结构,演化成一种三连杆式仿袋鼠腿悬架,并对其垂向特性开展研究。研究发现,该结构具有良好的缓冲隔振性能和控制特性,但阻尼缓冲元件采用直弹簧并联阻尼器的结构形式,仿生关节角度变化时,其处于非线性摆动拉压状态,不能很好地适应袋鼠腿姿态调节的旋转运动[11-12]。因此,本文在前期研究的基础上,设计一种双圆弧道缓冲阻尼结构[13],模拟袋鼠腿跳跃运动中筋腱、肌肉等组织的缓冲减振效果,并将其布置于悬架的仿生关节处,构建出一种含圆弧形缓冲阻尼结构的仿袋鼠腿悬架。为研究所提悬架的行为特性,本文构建出含圆弧形结构的三连杆式仿袋鼠腿悬架,建立Lagrange 1/4车辆动力学模型及ADAMS仿真模型,分析参数特性并与传统悬架进行对比分析,以验证所提悬架设计的有效性和合理性。

1 含圆弧形结构的仿袋鼠腿悬架构建

根据文献[14],袋鼠大腿长度约占腿部总长度的23%,小腿长度约占46%,脚趾长度约占31%,小腿长度约为大腿长度的两倍,即其腿部结构长度比为1∶2∶1.35。剖析袋鼠腿的运动发现:姿态调节主要通过腿部骨骼绕其关节做平面旋转运动来实现;缓冲减振性能主要依靠腿部肌腱和肌肉在神经系统自适应控制下调节腿部的姿态来实现。

本文依据袋鼠腿骨骼比例设计仿生大腿骨杆、小腿骨杆及足骨杆。为适应袋鼠腿姿态调节的旋转运动及缓冲减振性能的有效实现,设计一种双圆弧道缓冲阻尼结构替代直弹簧结构,以模拟袋鼠腿跳跃运动中筋腱、肌肉等组织的缓冲减振效果,并将其布置于仿生关节处,构建出含圆弧形结构的三连杆式仿袋鼠腿悬架,见图1。

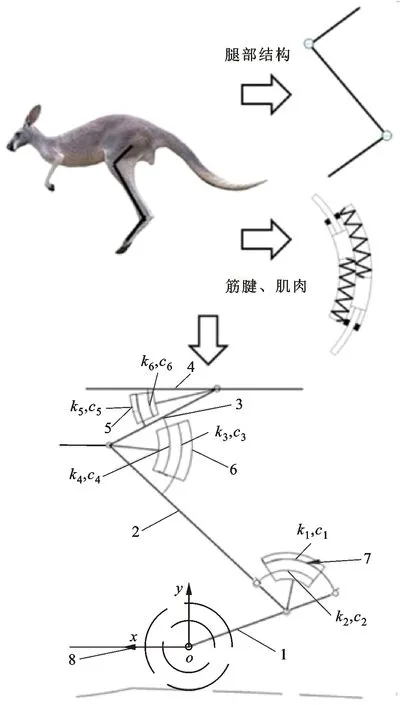
1—足骨杆;2—小腿杆;3—大腿杆;4—简化车身;5—踝关节弹簧阻尼器;6—膝关节弹簧阻尼器;7—髋关节弹簧阻尼器;8—车轮。图1 含圆弧形结构的三连杆式仿袋鼠腿悬架的构建Fig.1 Construction of the three-link bionic kangaroo leg suspension with circular arc-buffer structures

本文选取某中型车辆为参考车型,设定悬架静平衡高度为0.4 m[15],1/4车辆簧载质量为400 kg[16],悬架压缩与回弹的最大行程为0.1 m[17]。悬架的杆长根据静平衡位置及悬架的行程来确定。悬架关节弹簧阻尼器的刚度和阻尼系数通过ADAMS仿真试算确定,具体的悬架设计参数如表1所示。在实际运动中,由于存在着圆弧形导轨壁对弹簧的运动约束,弹簧的动刚度会相对表1所列的刚度发生变化。

表1 仿生悬架设计参数

2 含圆弧形结构的仿袋鼠腿悬架动力学建模

含圆弧形结构的三连杆式仿袋鼠腿悬架的动力学简图如图2所示。为了便于建模和分析,现做以下假设:①各连杆质量均匀且集中在质心处;②连杆和圆弧形轨道均为刚性体,圆弧形弹簧为柔性体,可沿轨道被拉压;③各杆件和车身只绕铰接点作平动或相对转动,不考虑摩擦影响。

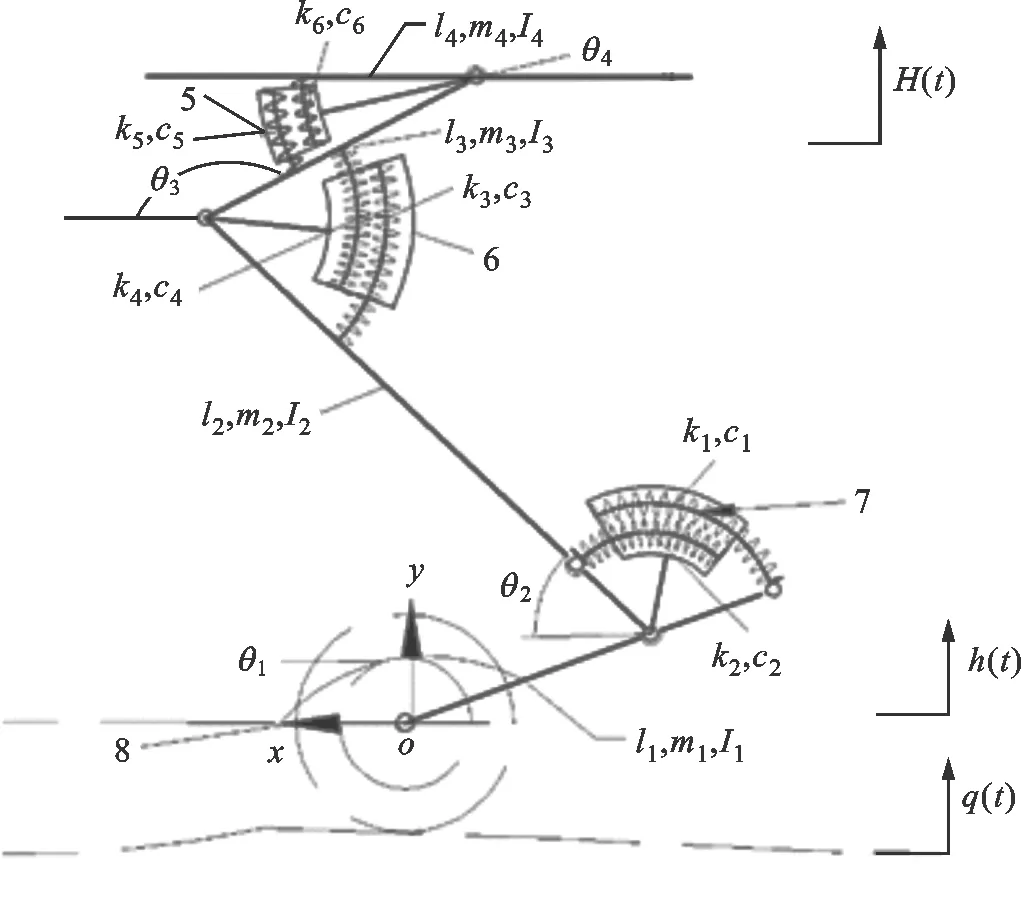
θ1—足骨杆与x轴正向夹角;θ2—小腿骨杆与x轴正向夹角;θ3—大腿骨杆与x轴正向夹角;θ4—车身与x轴正向夹角;h(t)—轮胎对路面不平度的响应;q(t)—路面激励。图2 含圆弧形结构的三连杆式仿袋鼠腿悬架动力学简图Fig.2 The dynamics diagram of the three-link bionic kangaroo leg suspension with circular arc structure

采用Lagrange方程法对仿生悬架进行动力学建模,以θ1～θ4为广义坐标,则仿生悬架动力学方程为

(1)

式中:L=T-V,T为系统总动能,V为系统总势能;D为系统总耗散能;Qi为广义坐标θi对应的广义力矩。所以,式(1)也可以写成

(2)

系统的总动能为

(3)

系统的总势能为

(4)

式中:d为弧形导轨的宽度;lki和lki0(i=1,2,…,6)分别为肌腱弹簧的原长和静平衡长度;Δxi为各弹簧静平衡下的变化量。

系统的总耗散能为

(5)

将式(3)～(5)能量表达式对广义坐标进行积分求解,之后代入式(2),得到对应的广义力矩。由于结果过于复杂,本文只给出θ4对应的广义力矩Q4

(6)

由式(6)知,悬架的角度、角速度及角加速度参数间存在着严重的非线性耦合关系,动力学特性参数的解析求解存在很大困难。因此,本文采用仿真建模和数值分析对该悬架进行动态特性研究[18-21]。

3 含圆弧形结构仿袋鼠腿悬架仿真建模

3.1 圆弧形弹簧的三维模型

本文采用Pro/E进行圆弧形弹簧的实体建模,并导入ADAMS中。圆弧弹簧的建模参数见表2。

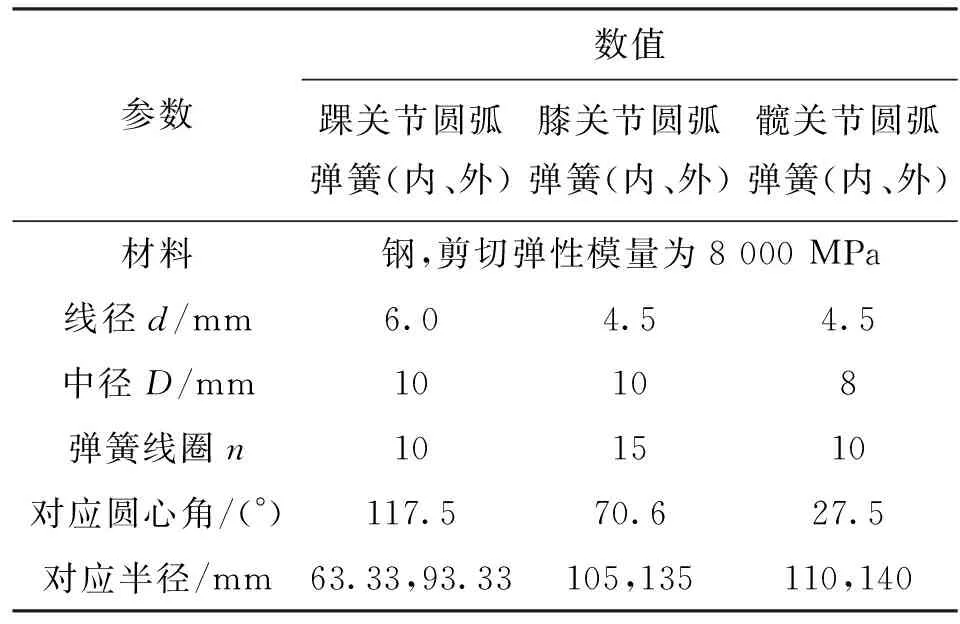
表2 圆弧形弹簧建模参数

将建立好的弹簧导入到ADAMS中,移动到需要的位置后与杆件固定副连接。由于弹簧在运动中两端挤压会产生较大变形,采用刚体设置难以模拟弹簧的变形,故采用ADAMS/View flex模块将弹簧处理成柔性体,见图3,使之满足悬架结构运动学及动力学的仿真要求。

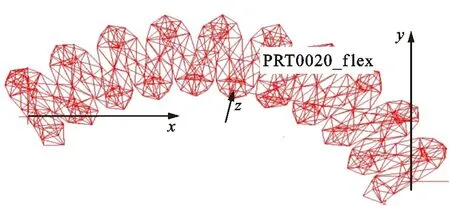
图3 柔性圆弧形弹簧Fig.3 Flexible circular arc spring

3.2 圆弧形弹簧的约束设置

本文借鉴文献[22-23]的思路,添加亚元结构与柔性体相连,并将约束加载到亚元结构,对圆弧形弹簧的运动进行等效,创建了双圆弧道约束。

本文建立的亚元为尺寸和弹簧线圈一致的圆环,将质量和转动惯量设置为0,并利用固定副将其与弹簧连接。选择有限的关键节点建立亚元,并创建亚元圆心与双圆弧道中心的共线约束,保证弹簧的圆周运动。

3.3 圆弧形仿生悬架仿真模型

采用3.1和3.2小节中的方法将6个弹簧都处理成柔性体并施加约束,建立1/4车辆仿生悬架ADAMS模型,见图4。为了便于建模中实现圆弧弹簧不同弧道运动的关联协同,将一根刚性连杆分别与双圆弧道(已隐藏)中的两个弹簧末端相连。当弹簧运动时,由于刚体连杆的不可拉压性和运动轨迹的限制,两根弹簧会实现协同运动。

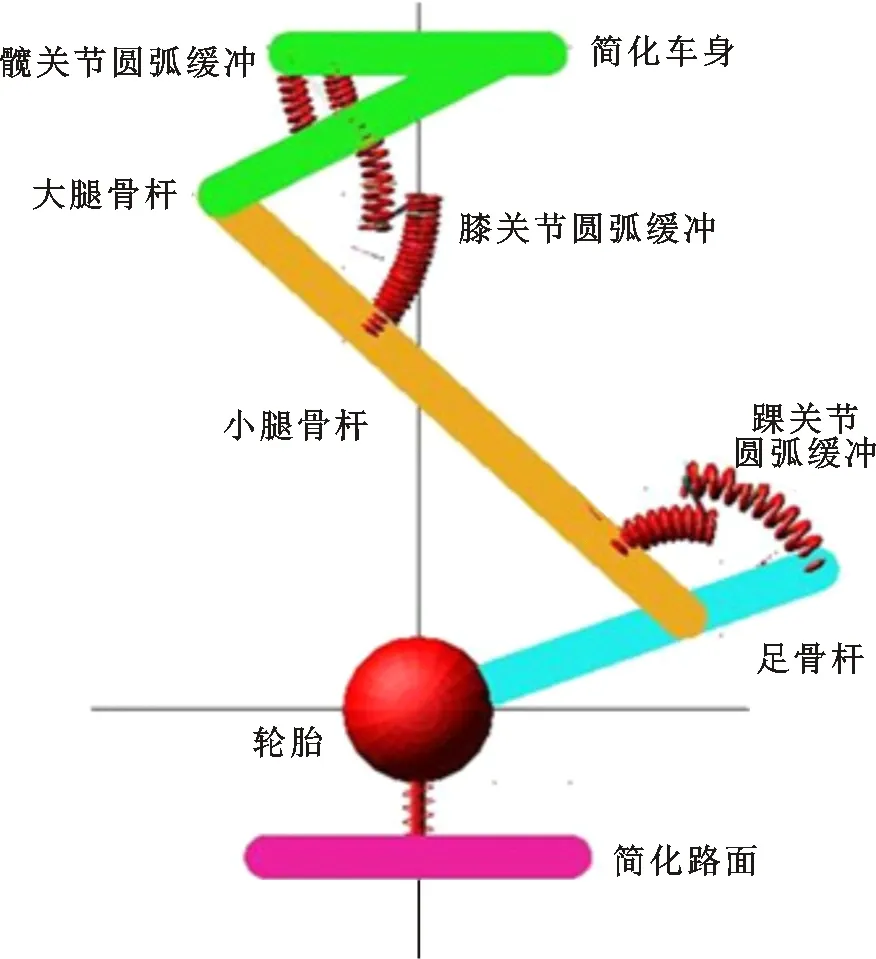
图4 仿生悬架仿真模型Fig.4 Simulation model of the bionic suspension

3.4 仿真路面模型

本文建立了利用滤波白噪声法得到的时域随机路面模型[24],并通过编辑STEP函数在ADAMS中生成了冲击路面模型。

4 仿袋鼠腿悬架被动特性仿真与分析

4.1 随机路面激励响应特性分析

采用3.4小节方法分别建立了A、B、C、D、E共5个等级的路面激励,并在A、B、C级路面下创建车速为30、60、90、120 km/h的4种路面激励,在D级路面下创建车速为30、60、90 km/h的3种路面激励,在E级路面下创建车速为30 km/h的路面激励。仿真时间设定为20 s。

为全面有效地探讨含圆弧形结构的仿袋鼠腿悬架的行为特性,本文以相同车速-不同路面等级和相同路面等级-不同车速为两种仿真方案,分别对车身垂向加速度、悬架动挠度、轮胎动位移等特性参数进行研究和讨论。因篇幅有限,仅给出部分仿真结果,见图5～13和表3。

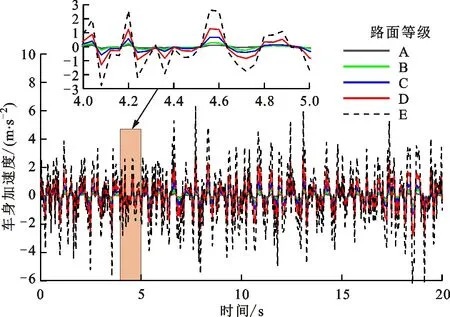
图5 30 km/h时不同路面等级下的车身加速度Fig.5 Body acceleration at 30 km/h on different grade roads

图5～8为车速30 km/h时5种路面等级(A～E)下的车身加速度(图5)、车身位移(图6)、悬架动挠度(图7)和轮胎动位移(图8)的时域响应,可以看出,这些响应均随着路面等级的增加而增加。由图5知,E级路面的车身垂向加速度最大,处于-6～6 m/s2间,在合理范围内。根据图7～8知,随着路面等级的增加,悬架动挠度(-35～30 mm)和轮胎动位移(-12～14 mm)响应均增加,且在合理范围内。

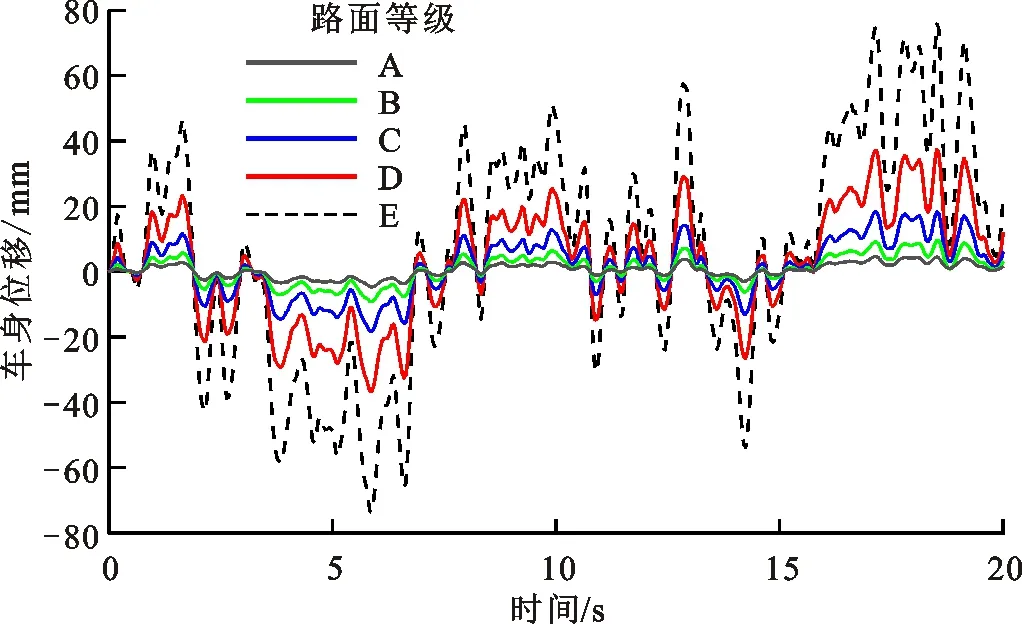
图6 30 km/h时不同路面等级下的车身位移Fig.6 Body displacement at 30 km/h on different grade roads

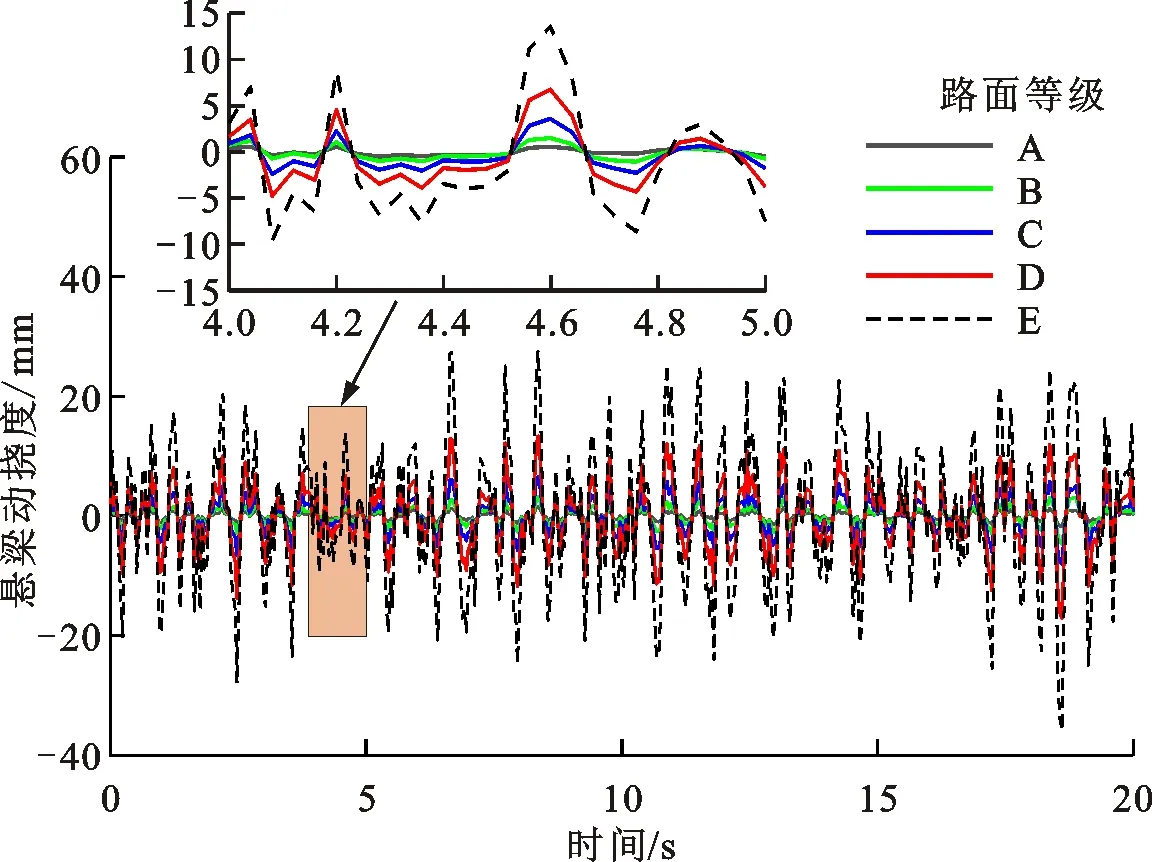
图7 30 km/h时不同路面等级下的悬架动挠度 Fig.7 Suspension dynamic deflection at 30 km/h on different grade roads

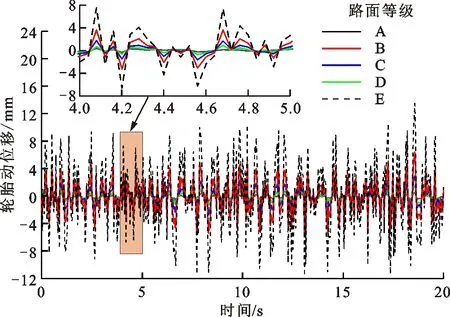
图8 30 km/h时不同路面等级下的轮胎动位移Fig.8 Tire dynamic displacement at 30 km/h on different grade roads

图9和图10对比了C级路面4种不同车速下的车身垂向加速度响应和轮胎动位移响应。可以看出,随车速的增加,车身垂向加速度和轮胎动位移也增加,但其增幅小于路面等级增加带来的影响。计算发现,悬架动挠度随车速的变化规律与车身垂向加速度的变化规律相似。此外,悬架在随机路面激励下的运动姿态调整较为平稳。

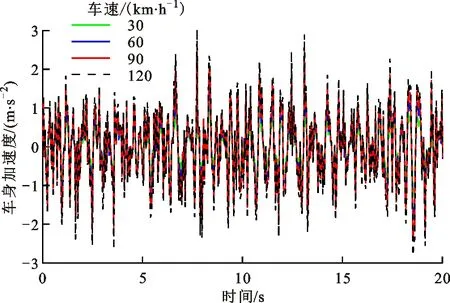
图9 C级路面不同速度下的车身加速度Fig.9 Body acceleration at different speeds on class-C road

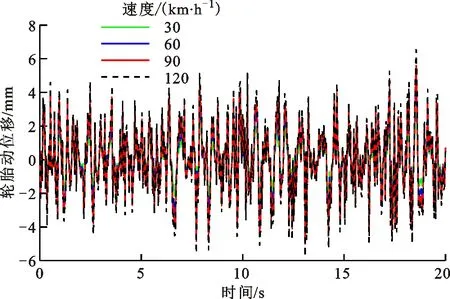
图10 C级路面不同速度下的轮胎动位移Fig.10 Tire dynamic displacement at different speeds on class-C road

在D级路面60 km/h车速激励下,仿生踝、髋、膝关节变化角度如图11～13所示。可以看出,悬架仿生关节角度的变化规律相似,表明其响应存在一定线性关系。仿生髋关节变化角度范围为22.3°～24.5°,最大角度差为2.2°;仿生膝关节变化角度范围为63.1°～66.7°,最大角度差为3.6°;仿生踝关节变化角度范围为124°～131.6°,最大角度差为7.6°;悬架整体仿生关节角度变化不大。

图11 仿生踝关节变化角度Fig.11 Angle change of the bionic ankle joint

为了进一步分析不同车速和路面等级对悬架响应的影响,将车身垂向加速度等悬架性能参数均方根及其传递率列于表3中。不同路面对应的车身垂向加速度和轮胎动位移相对增长率如图14和15所示。结合表3、图14和15可以得到以下结论。

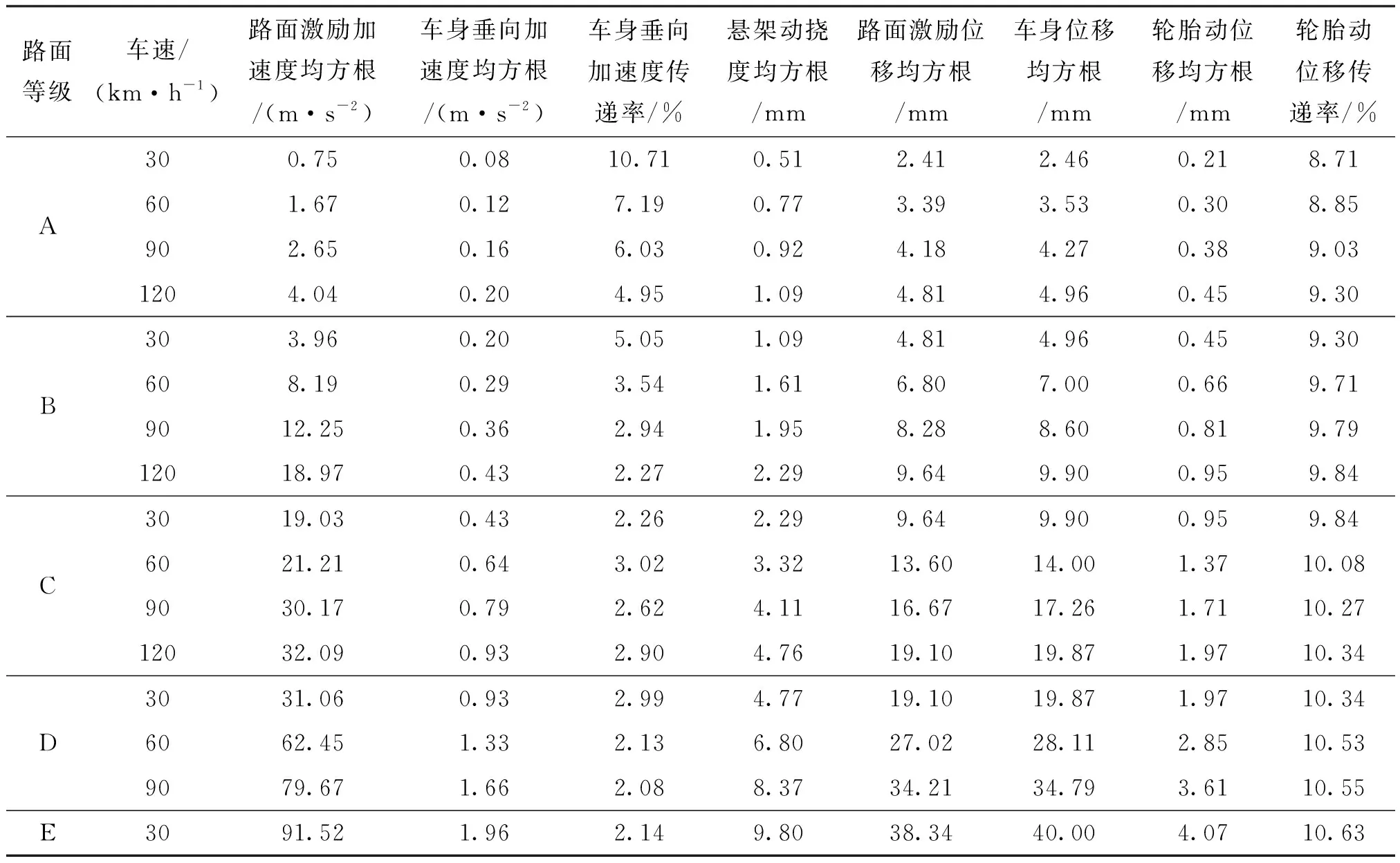
表3 含圆弧形缓冲结构仿袋鼠腿悬架的动态响应

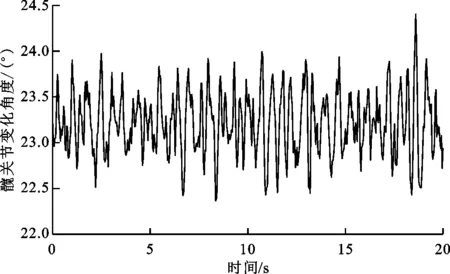
图12 仿生髋关节变化角度Fig.12 Angle change of the bionic hip joint

图13 仿生膝关节变化角度Fig.13 Angle change of the bionic knee joint

(1)车身垂向加速度、车身位移、悬架动挠度和轮胎动位移的均方根都随着路面等级和车速的增加而增加,且均在合理的范围内,表明本文所提仿生悬架结构设计合理。

(2)在相同路面等级下,随着车速的提高,车身垂向加速度(如图14所示)和悬架动挠度的均方根相对增长率降低。以C级路面为例:车速30 km/h时,车身垂向加速度均方根为0.43 m/s2;车速60 km/h时,车身垂向加速度均方根为0.64 m/s2,相对增长率为48.84%;车速90 km/h时,加速度均方根为0.79 m/s2,相对增长率为23.44%;车速120 km/h时,加速度为0.93 m/s2,相对增长率为17.72%。同理,悬架动挠度的相对增长率分别为45%、23.8%和15.82%。这表明仿生悬架具有良好的路面响应特性。从车身垂向加速度传递率数据可得:随着路面等级和车速的改变,车身垂向加速度传递率大致呈下降趋势,其中A级路面的传递率较大。除A级路面外,车身垂向加速度传递率在5%～2%之间,变化范围较小,表明该悬架具有良好的路面适应性和稳定良好的缓冲隔振性能。

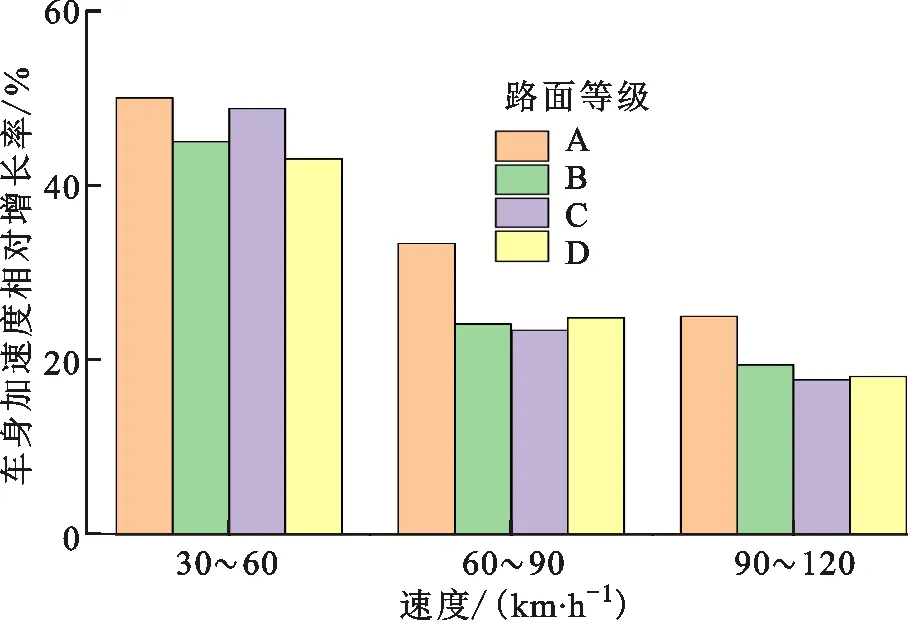
图14 车身垂向加速度相对增长率 Fig.14 Relative growth rate of the body vertical acceleration

(3)随着路面等级和车速的提高,轮胎动位移及其传递率总体均呈上升趋势,但轮胎动位移(0.21～4.07 mm)及其传递率(8.6%～10.6%)变化范围小且变化平稳,表明该悬架具有良好的稳定性和缓冲隔振性能;在相同路面下,随着车速的增加,轮胎动位移数值增加量减少及增加率呈明显的下降趋势(如图15所示),表明悬架高速稳定性更优;相对于车速的提高,路面等级的提高导致的轮胎动位移及其传递率增加更为明显,表明路面等级对轮胎动位移及其传递率的影响大于车速的影响。

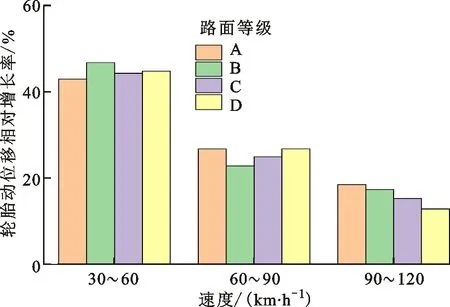
图15 轮胎动位移相对增长率Fig.15 Relative growth rate of tire dynamic displacement

4.2 冲击路面激励响应特性分析

冲击路面激励下车身的垂向动态位移如图16所示,车身垂向加速度如图17所示,各仿生关节角度如图18所示。从图16、17可以看出:仿生悬架经历正、负向激励后,车身位移相对路面激励降低约50%,车身垂向加速度相对路面激励降低约87%,且经历1.6 s左右车身质心回复至静平衡位置;相对于正向激励,仿生悬架对负向激励的位移及加速度的缓冲隔振效果略好;仿生悬架的被动模式能较好地隔离冲击路面激励。从图18可以看出:悬架经历正向冲击时,仿生踝关节、膝关节和髋关节角度呈先增大-减小-减小再调整的形式(13°,-6°,-4°);经历负向冲击时,仿生踝关节、膝关节和髋关节角度呈先减小-增大-增大再调整的形式(-14°,5.8°,3.3°);仿生踝关节处的角度变化最大;这些结果和袋鼠腿的运动特性相吻合,悬架表现出一定的仿袋鼠运动特征。

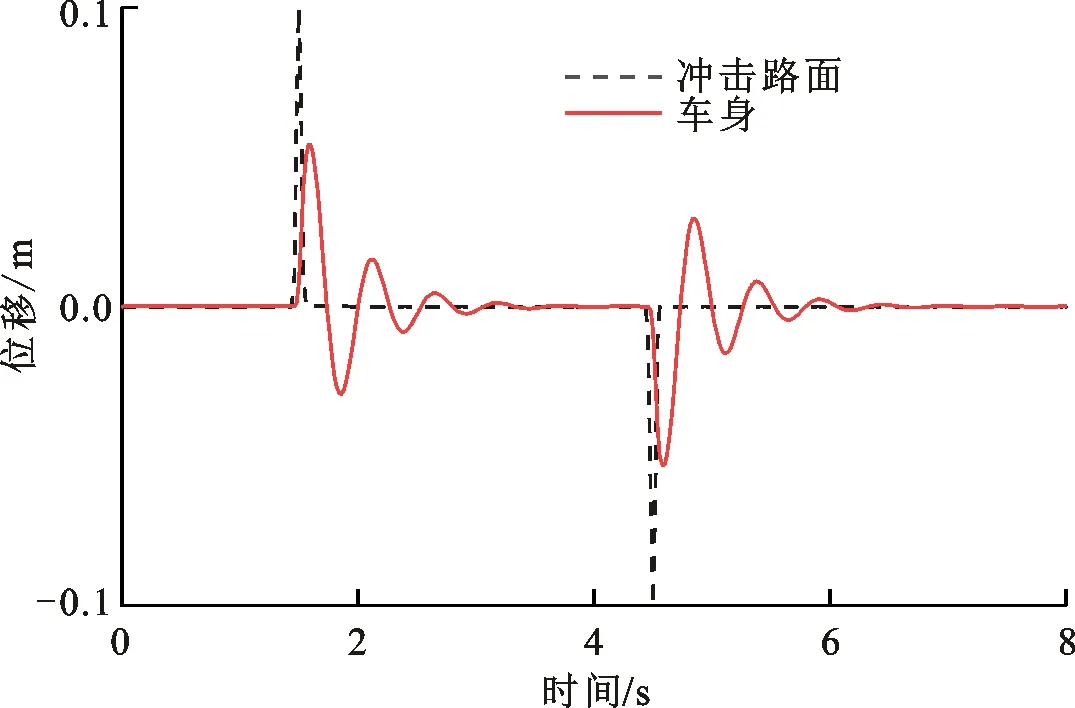
图16 冲击路面车身位移响应Fig.16 Body displacement response on impact road

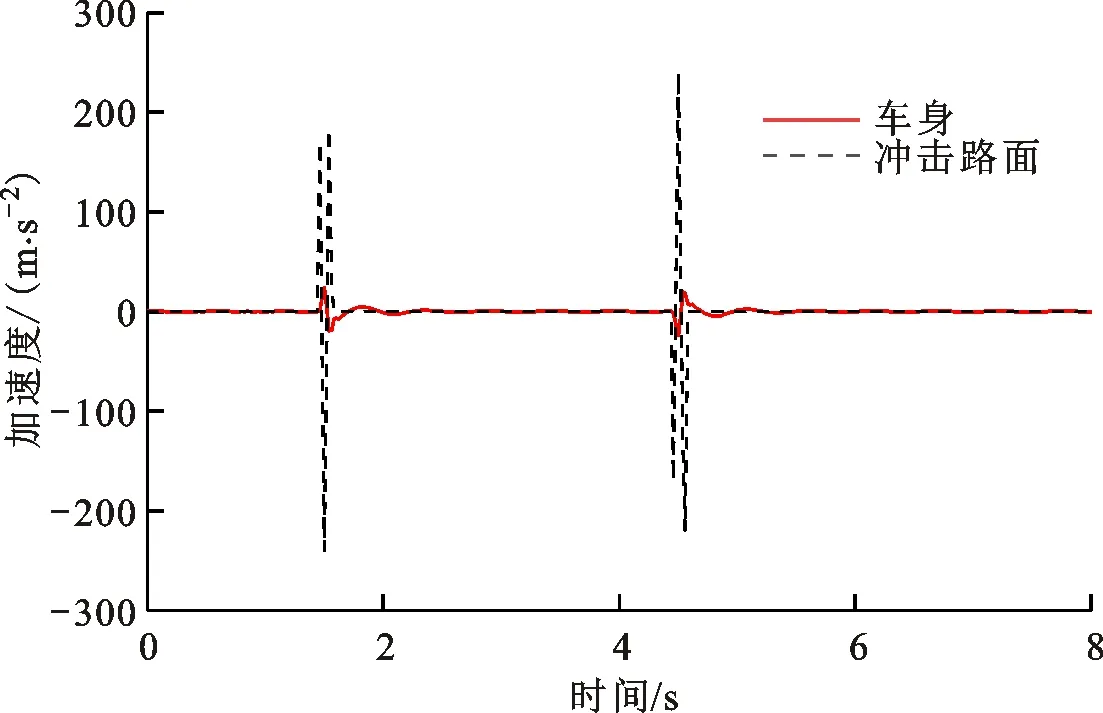
图17 冲击路面车身加速度响应Fig.17 Body acceleration response on impact road

图18 冲击路面仿生关节角度响应Fig.18 Angle response of bionic joint on impact road

4.3 仿生悬架与传统悬架性能对比分析

为了验证仿袋鼠腿三连杆悬架的性能,与文献[25-26]的传统悬架在同等条件下进行车身加速度、悬架动挠度和轮胎动位移均方根值的对比分析。对比工况为:①B级路面、车速20 km/h,C级路面、车速20 km/h;②B级路面、车速72 km/h,C级路面、车速50 km/h。对比结果如表4、5所示。

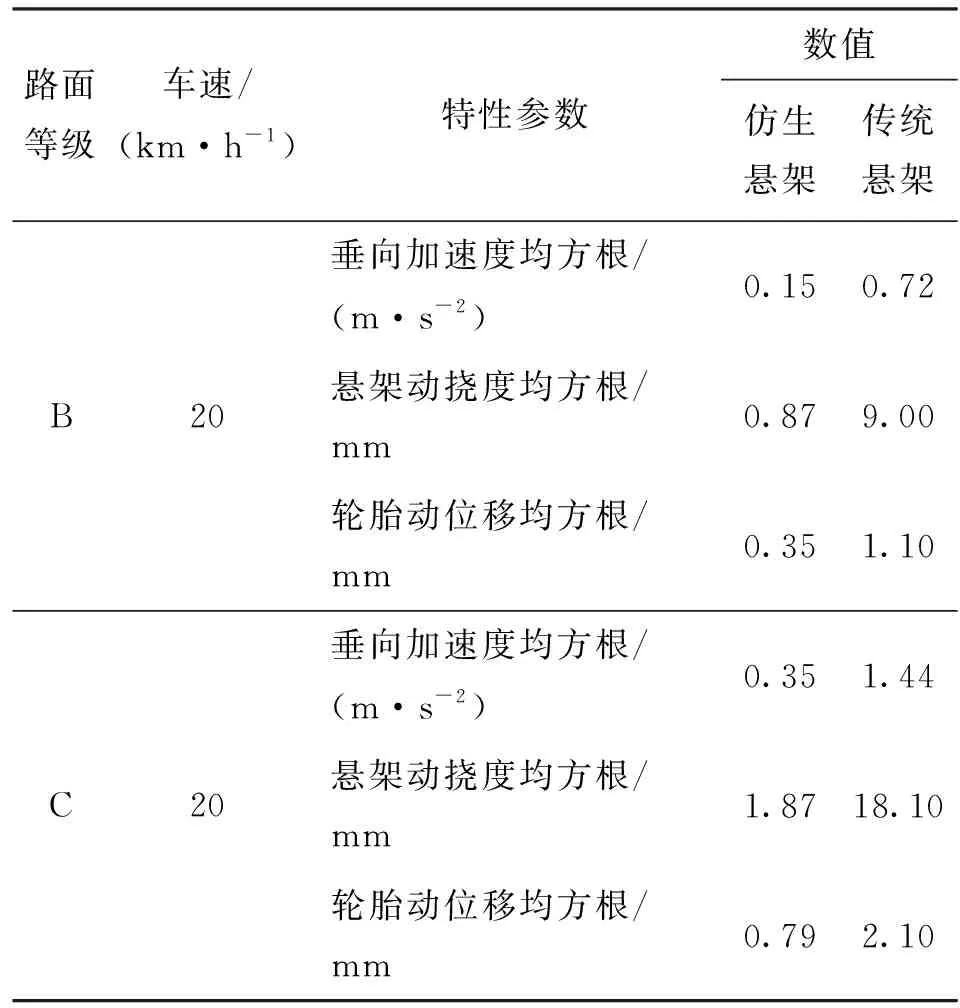
表4 仿生悬架与文献[25]中传统悬架特性参数的对比

从表4可知:在B级路面车速20 km/h时,仿生悬架垂向加速度均方根(0.15 m/s2)相对传统悬架(0.72 m/s2)降低了79.17%,悬架动挠度降低了90.33%,轮胎动位移降低了68.18%;在C级路面车速20 km/h时,仿生悬架垂向加速度均方根(0.35 m/s2)相对传统悬架(1.44 m/s2)降低了75.69%,悬架动挠度降低了89.67%,轮胎动位移降低了62.38%。从表5可知:在B级路面车速72 km/h时,垂向加速度均方根值相对传统悬架降低了76.76%,悬架动挠度降低了93.75%,轮胎动位移降低了82.56%;在C级路面车速50 km/h时,垂向加速度降低了75.53%,动挠度降低了93.67%,轮胎动位移降低了82.64%。结果表明,含圆弧形缓冲结构的仿袋鼠腿悬架各项被动特性均优于对比文献中传统悬架的,验证了悬架仿生设计的正确性和有效性。

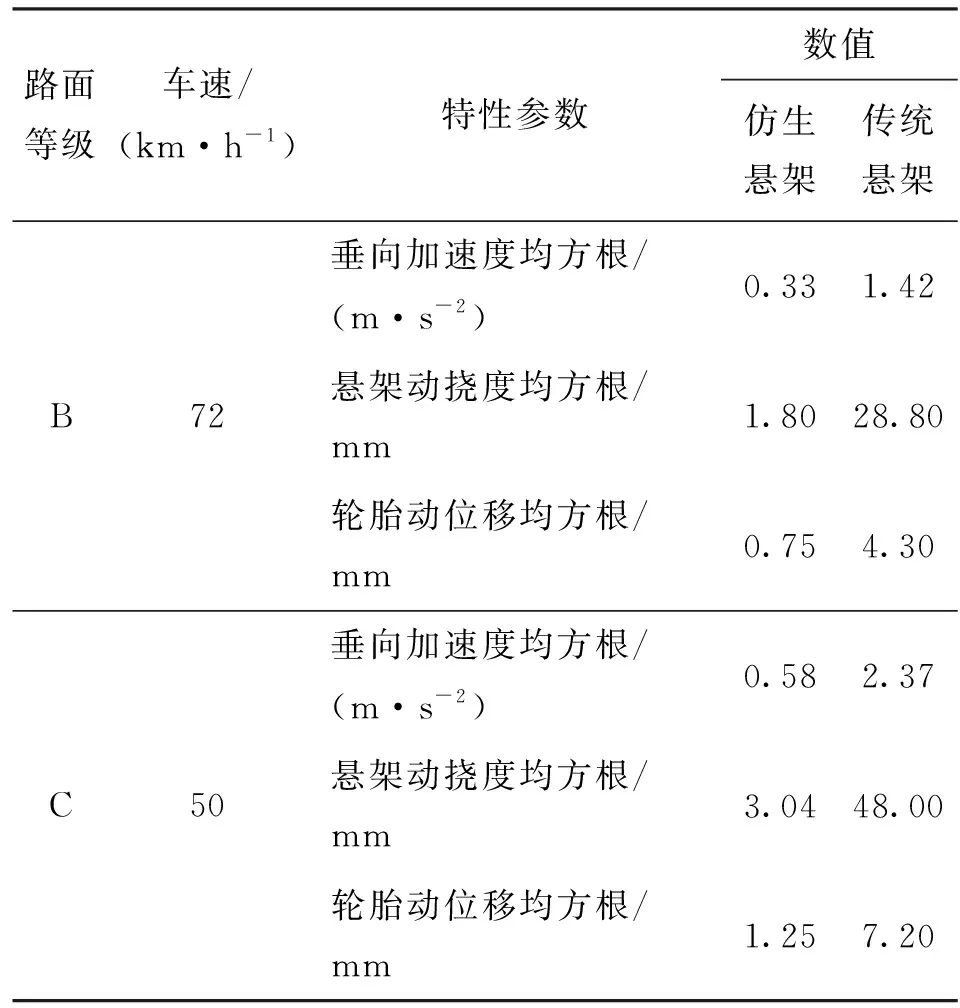
表5 仿生悬架与文献[26]中传统悬架特性参数的对比

4.4 频响特性分析

为分析含圆弧形缓冲结构的三连杆仿袋鼠腿悬架在频域下的传递特性,对其加速度传递特性进行频域响应分析。由于仿生悬架存在强烈的非线性耦合特性,解析法难以求出其频率传递函数,故用近似估计法进行求解,具体步骤可参考文献[15]和[27]。传递特性计算式为

(7)

因为三连杆存在严重非线性,故本文采用ADAMS的设计变量进行扫频以获得加速度的均方根。

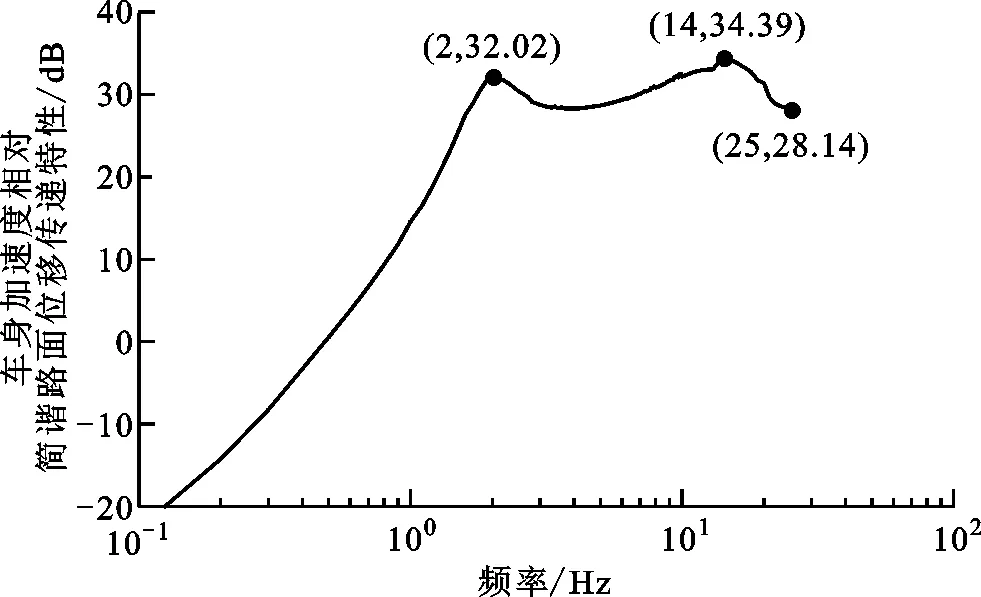
图19 车身加速度相对简谐路面位移传递特性Fig.19 Transmission characteristics of body acceleration relative to harmonic road displacement

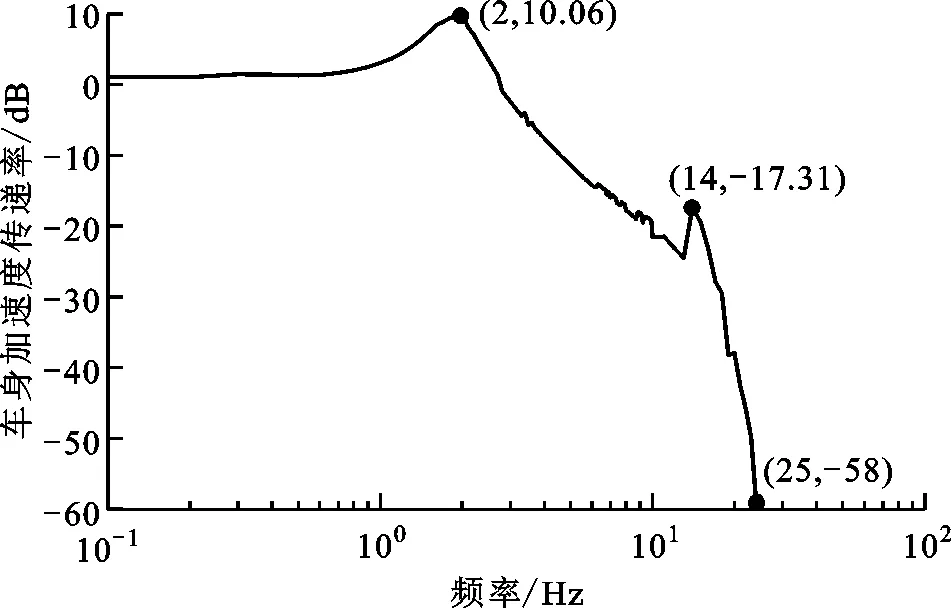
图20 车身加速度传递率频响特性 Fig.20 The frequency response characteristic of body acceleration transmissibility

5 结 论

为追求高品质的悬架,本文从仿生设计方案的角度出发,构建出一种含圆弧形缓冲结构的仿袋鼠腿三连杆悬架,进行了动力学建模和行为特性分析,得到以下结论。

(1)不同工况下,仿生悬架的特性参数均在合理范围内,表明悬架结构设计的合理性和可行性。

(2)相对于传统悬架,仿生悬架能够有效改善路面适应性、舒适性和稳定性,这与最初的研究目标相一致,验证了仿生思路的正确性和有效性。

(3)仿生悬架的车身和车轮固有频率在2 Hz和14 Hz左右,避开了人体敏感的频率区间,且车身加速度传递率最大值较小,表明悬架具有良好的频响特性,进一步验证了悬架结构设计的合理性。此外,车身固有频率略大,表明刚度阻尼等系数还有进一步优化的空间。