全断面隧道掘进机滚刀预切槽破岩数值模拟

耿麒,卢智勇,张泽宇,汪学斌,马茂勋,叶敏

(1.长安大学公路养护装备国家工程实验室,710064,西安;2.西藏天路股份有限公司博士后工作站,850000,拉萨)

全断面隧道掘进机(TBM)掘进硬岩时,如果滚刀破岩载荷不能驱动侧向裂纹相互贯通,就会导致刀刃反复碾磨掌子面,进而出现破岩效率低、掘进速度慢、滚刀磨损大的问题[1]。预切槽辅助滚刀破岩是目前业内正在探索的新技术[2],指利用高压水射流等非接触式破岩方法[3],在岩石中预先切割出凹槽以移除侧向约束,将岩石由三轴受压状态转变为单轴受压状态,提高滚刀破岩效率。

将国内外水射流破岩研究归纳如下。第一,水射流辅助机具破岩,例如,Ciccu等进行了纯水射流辅助切刀和滚刀切削软岩的试验,发现破岩载荷明显降低,破岩效率显著提升[4-5];Tang等研制了一种磨料水射流辅助破岩钻头,利用钻头中部喷出磨料高压水和外部刀齿组合切削软岩和硬岩,发现钻进速度显著提升,钻头磨损明显下降[6-7];Liu等进行了纯水射流辅助切削中硬岩、磨料水射流辅助切削硬岩的试验和数值模拟研究,发现破岩载荷最大可降低45%[8-9]。第二,水射流直接破岩,例如,Oh等进行了磨料水射流直接切削岩石的试验研究,揭示了岩石强度、水压力、喷嘴移速等参数对切槽深度和切削效率的影响规律[10];Kim等进行了磨料水射流切削混凝土和岩石的试验研究,分析了喷嘴移速和转速对破岩效果的影响规律[11];Karakurt等进行了磨料水射流切削花岗岩的试验研究,揭示了喷嘴距离、移速和磨料参数对切槽宽度的影响规律[12];Dehkhoda等进行了脉冲纯水射流破岩试验研究,揭示了表面成孔和裂纹萌生机制,分析了脉冲长度和频率对破岩效果的影响规律[13]。分析表明,上述研究集中在水射流减小机具载荷、提高破岩效率、降低机具磨损的印证方面,以及水射流参数对切槽结构的影响等方面,然而在何种切槽结构更有利于滚刀破岩方面的研究相对匮乏。

将滚刀破岩的颗粒离散元数值模拟研究归纳如下:孙金山等建立了滚刀破岩二维数值模型,研究了滚刀刃数、刀间距、结构面强度、角度和间距等参数对破岩过程的影响[14];谭青等建立了滚刀破岩的二维数值模型,研究了刃宽、刃角、刀间距、贯入度等参数对破岩载荷、比能和裂纹深度的影响规律[15-16];Moon等建立了双刀顺次贯入岩石的二维数值模型,研究了刀间距和贯入深度对破岩比能的影响规律[17];Cho等进行岩石破坏模拟,指出直接使用平行黏结键聚合的岩石模型的抗压与抗拉强度之比远小于实际值,而使用颗粒簇或颗粒块技术可有效克服该缺陷[18];Li等建立了楔刀破岩二维数值模型,研究了岩石破坏过程中的裂纹和应力分布变化规律[19];Zhang等分别建立了二维和三维的滚刀破岩数值模型,研究了节理与软硬不均岩层对破岩过程的影响规律[20-21]。预切槽辅助滚刀破岩方面,仅见汤胜旗等研究了围压、预切槽间距和深度对楔刀静压贯入花岗岩的影响[22]。分析表明,现有研究主要针对常规TBM滚刀破岩过程,对预切槽辅助滚刀破岩过程研究较少,而且模拟大多使用平行黏结键直接聚合形成岩石的方法,不易准确标定岩石强度,进而可能影响模拟结果的可靠性。

采用颗粒离散元软件PFC2D构建了基于优化泰森多边形算法的等效晶质岩石材料数值模型,进行多组预切槽辅助的滚刀破岩过程数值模拟,研究了切槽角度、位置、间距等结构参数对破岩载荷和破岩效率的影响规律。结果表明:基于预切槽弱化围岩和密实核传力驱动双重机制的预切槽辅助滚刀破岩方法可极大提高硬岩破碎效率,“窄直切槽、错缝切削、滚刀中置”是最优的切槽结构及排布模式。

1 等效晶质岩石材料建模与标定

1.1 岩石材料颗粒簇离散元建模

颗粒离散元法擅长从细观力学角度解释材料的损伤断裂机制,由于岩石材料在高倍显微镜下呈现颗粒结构,因此将岩石视为颗粒离散介质是可行的[16]。PFC2D软件采用颗粒聚合的方法表征岩石材料,即通过在相邻圆形颗粒间施加线性平行黏结键,使颗粒接触区域具备一定的弹性和抵抗拉伸、剪切、扭转的能力,从而呈现与实际岩石相似的宏观力学性质。已有研究[18-19]表明,直接采用线性平行黏结键聚合而成的岩石,其单轴抗压与抗拉强度的比值远小于实际岩石,这是由于圆形颗粒间的平滑接触边界不具备实际晶状岩石粒料的嵌合与自抗扭能力,从而低估了聚合而成岩石的抗压强度。

针对上述问题,基于优化泰森多边形算法的颗粒簇岩石材料建模流程如图1所示。将岩石区域用德洛尼三角划分网格;将各个德洛尼三角的外接圆圆心围绕各三角顶点相连;删除德洛尼三角网格,余下的各边将区域划分为泰森多边形网格,如图1a中的各多边形;将岩石模型区域用圆形颗粒填充;根据已划分的泰森多边形网格将颗粒分组,各组内的颗粒聚合表征各个晶粒,同组内的颗粒用相同颜色表示,如图1b所示;对所有颗粒与墙体接触赋予线性模型,如图1c中红色短线所示,对所有颗粒间的接触赋予线性平行黏结模型,对晶内(图1c蓝色短线)和晶间(图1c绿色短线)颗粒的接触模型参数分别进行标定和赋值。为了规避由于晶粒的形状和尺寸过于随机而带来的误差,本文对Matlab软件自带的voronoi函数进行优化,通过合理控制德尼洛三角顶点的分布位置而生成排布较为均匀的泰森多边形。

(a)区域划分 (b)颗粒填充 (c)接触设置 图1 基于优化泰森多边形算法的颗粒簇岩石材料建模流程Fig.1 Modeling of the cluster-based rock material using an optimized Tyson polygon algorithm

该方法具有如下特点:可以模拟压缩导致的晶粒破裂,以及晶界在剪切、张拉和膨胀作用下错动或分离而产生的裂纹,与实际情况接近;不规则的晶粒边界不仅可以促进张拉裂纹的扩展,还可以提高晶粒间的抗扭转能力。因此,所构建的岩石与实际岩石的宏观力学特性非常接近。

1.2 细观参数标定

细观参数标定过程如下:针对本文所研究的秦岭花岗岩,按照国际岩石力学学会推荐的试验方法进行单轴压缩和巴西劈裂试验,各进行5次,获取岩石试件的宏观物性参数,求取平均值;选取适当的岩石细观力学参数构建岩石模型,进行单轴压缩和巴西劈裂仿真,使岩石模型和试件呈现相近的宏观物性参数。参照已有研究[18-19],设定单轴压缩和巴西劈裂仿真的加载速度均为0.01 m/s,时间步长为5.5×10-8s,确保模拟处于准静态平衡状态。Li研究表明,颗粒尺寸效应对模拟结果影响较小[19];Potyondy研究表明,颗粒直径小于0.73 mm时岩石宏观物性参数基本不变[23],但颗粒总数随着颗粒直径的减小而迅速增大,进而延长计算时间,因此经过多组试算,综合考虑颗粒直径对模拟精度和计算时间的影响,选取颗粒平均直径为0.5 mm,模拟计算所确定的岩石细观力学参数如表1所示,使用该套参数进行模拟,所获取的岩石宏观物性参数如表2所示,单轴压缩和巴西劈裂的仿真和试验结果如图2所示。结果表明,岩石模型和试件的宏观物性参数非常相近,弹性模量、泊松比、抗压强度、抗拉强度4项参数的误差均小于4%;单轴压缩与巴西劈裂仿真和试验的岩石宏观破坏模式相似,单轴压缩呈现斜切破坏,巴西劈裂呈现中部劈裂破坏;单轴压缩仿真和试验的应力应变曲线相近,但模拟的轴向应变值略小于试验值,因为岩石材料受载初始阶段,原有微裂隙逐渐闭合,使岩石被压密而形成早期的上凹形非线性变形,所构建的岩石模型暂不能模拟微裂隙压密过程。上述结果说明了本文岩石材料颗粒簇离散元建模方法的可靠性。分析产生的裂纹,采用青、红、绿、蓝4种颜色分别表示晶间张拉、晶内张拉、晶间剪切、晶内剪切4种裂纹,发现单轴压缩仿真中张拉裂纹占84.0%,晶间张拉裂纹占60.7%,巴西劈裂仿真中张拉裂纹占85.4%,晶间张拉裂纹占56.3%,表明岩石破坏的主要形式是晶粒间的张拉破坏。

表1 岩石细观力学参数

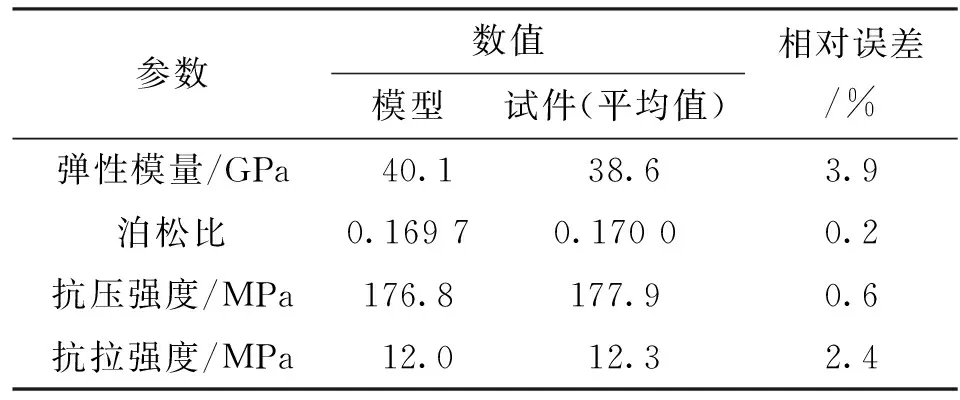
表2 岩石宏观物性参数

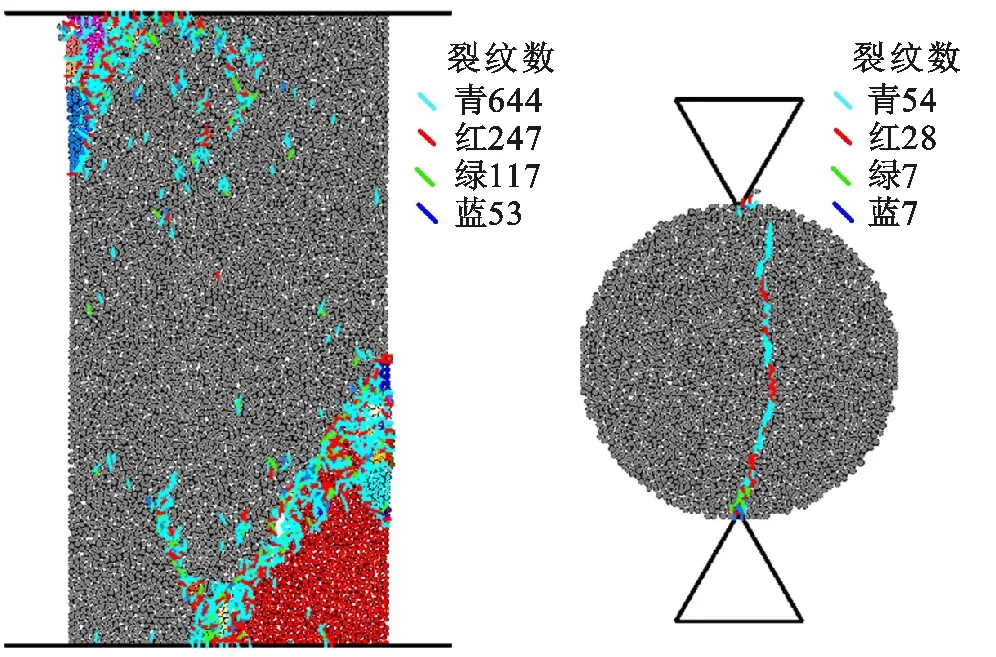
(a)单轴压缩仿真 (b)巴西劈裂仿真

(c)单轴压缩试验 (d)巴西劈裂试验

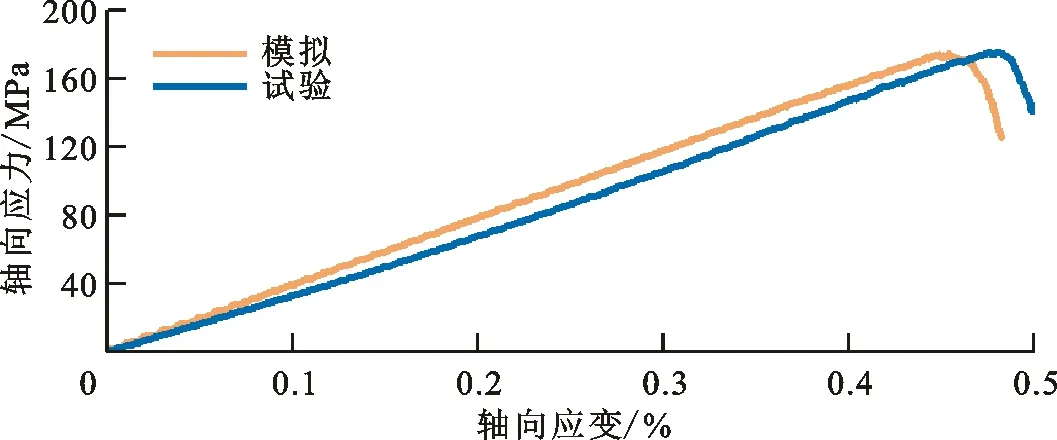
(e)单轴压缩模拟与试验的轴向应力应变曲线图2 单轴压缩与巴西劈裂的仿真和试验结果Fig.2 Simulation and experimental results of uniaxial compression and Brazilian splitting

2 滚刀预切槽破岩模型与试验验证

2.1 滚刀预切槽破岩模型

(a)错缝切削

(b)同缝切削

(c)混合切削图3 滚刀预切槽破岩模型 Fig.3 Numerical model for rock indentation assisted with pre-cut grooves

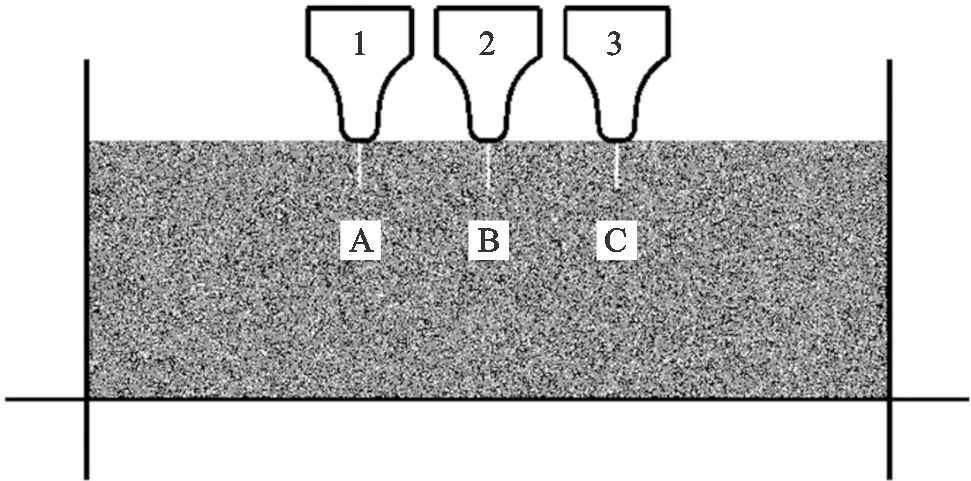
滚刀预切槽破岩模型如图3所示,包括错缝切削、同缝切削和混合切削3种模式,错缝切削是指预切槽位于滚刀贯入位置两侧,同缝切削是指预切槽位于滚刀贯入位置正下方,混合切削是前两种模式的组合。滚刀的初始位置距岩石上表面为0.3 mm,设定滚刀竖向最大位移为2.3 mm,设定岩石模型宽度为500 mm。为了选取合适的模型高度,针对错缝切削模式,分别进行高度为400 和200 mm的滚刀破岩模拟如图4所示,发现两个模型的岩石破碎效果、裂纹分布、滚刀破岩载荷均非常相似,两次模拟时间分别为3.1 h和1.4 h,因此选取模型高度为200 mm。岩石模型约由3.1万个晶粒、11.3万个颗粒组成。选用直径432 mm、刃宽20 mm的平刃滚刀。滚刀贯入速度为0.1 m/s,时间步长为5×10-8s,滚刀贯入速度折算为5×10-9m/步,确保模型为准静态模型。采用CPU Intel-Core-i9-10980XE、内存64 GB的计算机配置进行数值模拟。

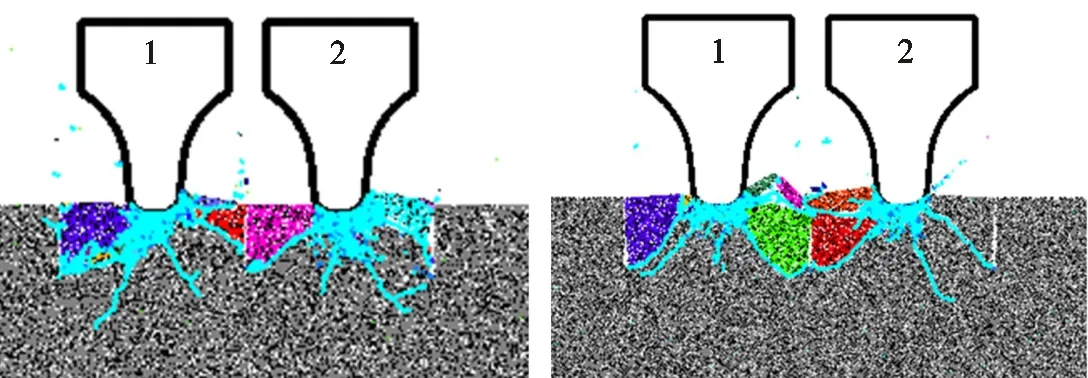
(a)高度400 mm模型 (b)高度200 mm模型

(c)滚刀破岩法向力图4 高度为400和200 mm的滚刀破岩模拟Fig.4 Rock indentation simulations for the 400 and 20 mm height models

2.2 数值模型试验验证

为验证本文所建数值模型的可靠性,进行如图5所示小型静压破岩试验与数值模拟。滚刀预切槽破岩和临空面破岩类似,因此参考已有研究[24],基于长安大学材料学院Landmark370.10型多功能材料试验机,进行2组小型单侧临空面静压破岩试验。本文为二维数值模型,为了更合理地验证数值模型,将岩石试样加工成150 mm×100 mm×24 mm的片状,以减小模型厚度方向的不一致性,试样表面经过打磨处理。将岩石试样夹持到夹具中,左侧具有70 mm高度的临空面,为了保证各个面受力均匀,在岩石与夹具的接触面上粘贴橡胶垫。夹具下部设置有滑轨滑块结构,将滑块下部夹持于试验机下压头中,夹具可沿滑块左右移动以实现刀具贯入位置的调整,刀具嵌入夹头中部凹槽中,夹头夹持于试验机上压头中。试验1和2中的刀具贯入位置距左侧临空面分别为30和15 mm。如图5c所示,刀1和2刃部半径均为25 mm,厚度为5 mm,刀1刃部有1 mm×45°倒角,刀2为平刃。

(a)破岩试验1 (b)破岩试验2

(c)试验用刀具 (d)密实核形态

(e)破岩模拟1 (f)破岩模拟2图5 小型静压破岩试验与数值模拟Fig.5 Small scaled rock indentation tests and simulations

下压头保持不动,上压头以1 mm/min的加载速度下压。试验1和2的峰值载荷为16.9和19.1 kN。如图5d所示,对破裂后的试样断面进行处理,发现刀刃贯入位置正下方有一个三角形密实核,宽度为9 mm;由于刀刃端部接岩区域近乎平直,因此假定刀刃与密实核接触区域压力均匀分布。将模拟1和2的峰值载荷换算到三维情况,即用模拟所得二维载荷乘以密实核宽度,得到实际载荷分别为15.4和19.9 kN,与试验载荷的误差分别为8.9%和4.2%,说明模拟和试验的峰值载荷误差较小。试验1和模拟1中岩碴呈三角形楔块状,而试验2和模拟2中岩碴呈窄条状,试验和模拟的岩石破坏形式相似,也与其他学者已有研究结果[24]类似。上述分析说明,数值模拟和试验的结果吻合度较高,验证了本文所建刀具破岩数值模型的可靠性,也进一步验证了本文岩石材料建模方法的可靠性。

3 滚刀预切槽破岩数值模拟及分析

3.1 预切槽角度对破岩效果的影响

已有研究表明,由水射流制备的预切槽开口角度较小[10],而由激光等方式制备的预切槽角度较大[25]。基于图3a所示的错缝切削模式,设定滚刀间距为120 mm、预切槽深度为30 mm、滚刀最大竖向位移为2.3 mm、滚刀距左右切槽的距离均为60 mm、预切槽角度分别为120°、100°、80°、60°、40°、20°和0°,建立7组模型。预切槽角度对破岩效果的影响如图6所示,各组模拟的宏观裂纹分布基本一致,当侧向裂纹贯通至预切槽根部时有片块状岩碴形成;当预切槽角度大于120°时,侧向裂纹不能贯通至预切槽根部,因而无大块岩碴;随着预切槽角度减小,岩碴形状由三角片状逐渐演变为三角块状,单块岩碴面积逐渐增大;当预切槽角度小于20°时,滚刀2下方的裂纹不能贯通至预切槽根部,因而无大块岩碴。由于各组模型中两把滚刀的贯入状态及刀下岩石破坏模式相似,因此仅给出滚刀1的法向力如图6b所示,各组模型的法向力曲线形态基本相似,一次完整的贯入循环过程包括加载、卸载和低值波动3个阶段,分别对应刀下密实核的压密、破裂和崩坏3个阶段;随着预切槽角度的减小,法向力峰值略有增大,这是因为更大的预切槽角度意味着预先去除了更多的岩石材料,从而对滚刀贯入区域的侧向约束力更小。对于本小节的大刀间距(120 mm)模型,由于侧向裂纹的生长方向具有一定的随机性,一旦某条侧向裂纹贯通至一侧的预切槽根部,刀下密实核发生崩坏和应力释放,就无法继续传递载荷从而驱动另一侧的侧向裂纹和预切槽相互贯通,因此需要合理设置槽间距和预切槽结构,确保滚刀两侧的岩石均衡破碎。计算7组模型的贯入比能如图6c所示,即产生单位面积岩碴的法向力做功[24],用于评价破岩效率,比能与破岩效率成反比;随着预切槽角度的增大,贯入比能总体上成先减小、后稳定、最后增大的变化规律,预切槽角度介于40°～100°时贯入比能最小、破岩效率最高,这与上文对岩碴形式的分析一致。

(a)不同预切槽角度下的岩石破碎效果

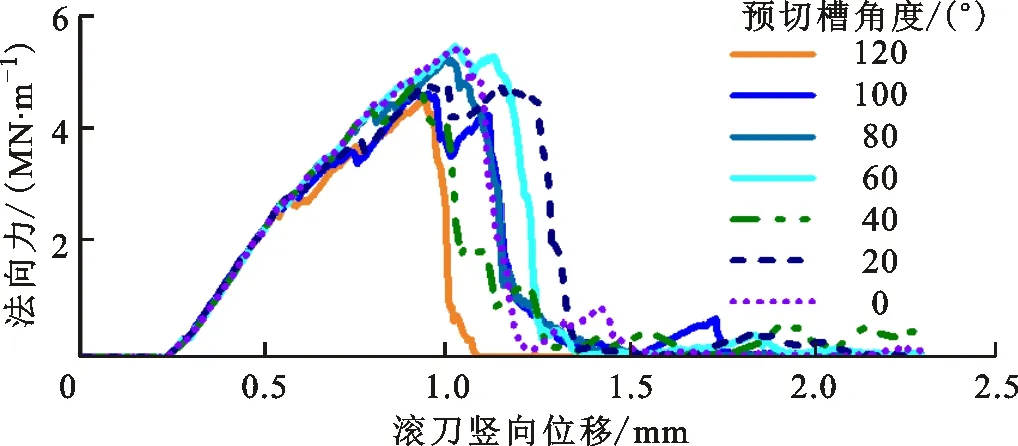
(b)滚刀1破岩法向力

(c)滚刀贯入比能图6 预切槽角度对破岩效果的影响Fig.6 Influence of the angle of pre-cut grooves on rock fragmentation

上述分析说明,为提高破岩效率,预切槽角度不得大于120°,建议取值为40°～100°,然而现有水射流技术制备的预切槽角度一般为0°,而此时的破岩效率相较于40°～100°预切槽角度情况并未显著降低,因此,综合建议最优预切槽角度为0°。

3.2 切削模式对破岩效果的影响

为对比有无预切槽对破岩效果的影响,建立两组破岩模型,设定无预切槽模型滚刀间距为80 mm,设定有预切槽模型的预切槽间距为80 mm、深度为30 mm、宽度为2 mm、滚刀位于相邻预切槽正中且间距为80 mm,两组模型的滚刀最大竖向位移为2.3 mm。有无预切槽对破岩效果的影响如图7所示,无预切槽模型的破岩机理通常是相邻滚刀间的侧向裂纹相互贯通[1],然而本文所研究的硬岩抗压强度近180 MPa,直至主裂纹充分发育、密实核破裂,刀间的侧向裂纹仍未贯通成碴;而对于有预切槽破岩模型,刀下的侧向裂纹朝预切槽方向主动生长并贯通成碴,相邻滚刀之间的联动作用虽然被弱化,但岩石侧向约束亦被削弱,刀下岩石被充分破碎为三角块状岩碴。无预切槽模型的滚刀破岩法向力峰值是有预切槽模型的1.8倍,同时前、后者的贯入比能分别为43.0和2.2 kN/mm2,前者是后者的19.5倍,说明预切槽可有效降低滚刀破岩载荷,显著提高滚刀破碎硬岩的效率。

(a)有预切槽 (b)无预切槽

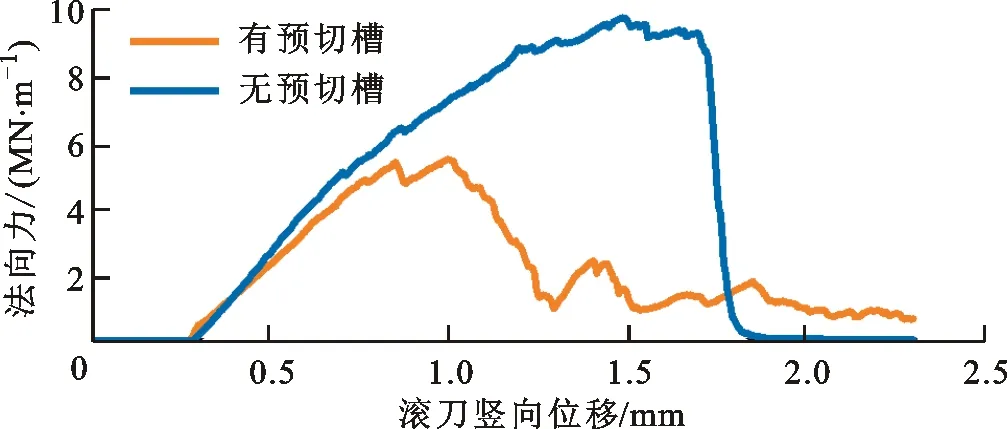
(c)滚刀1破岩法向力图7 有无预切槽对破岩效果的影响Fig.7 Comparison of rock fragmentation results with and without the assistance of pre-cut grooves

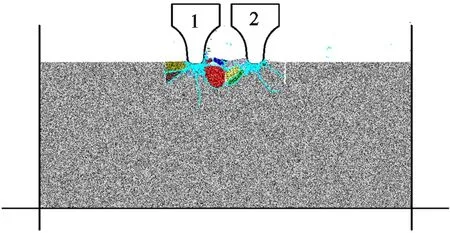
(a)错缝切削

(b)槽宽2 mm的同缝切削

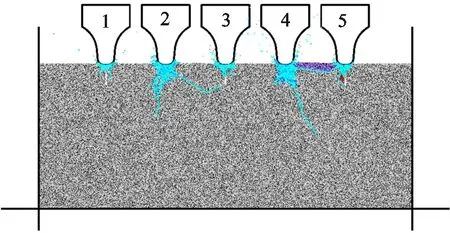
(c)混合切削

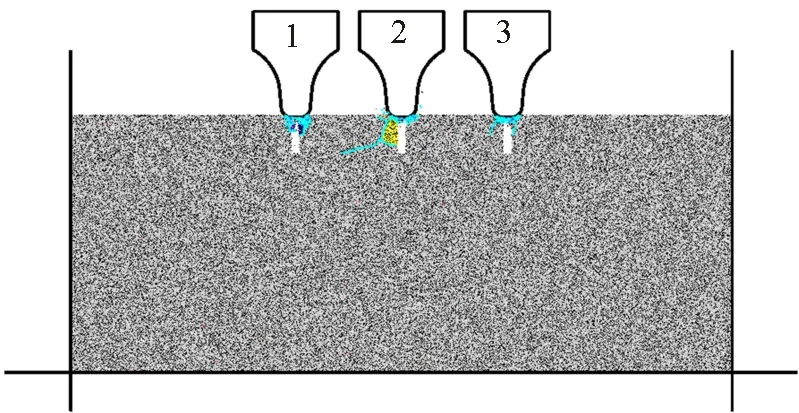
(d)槽宽5 mm的同缝切削

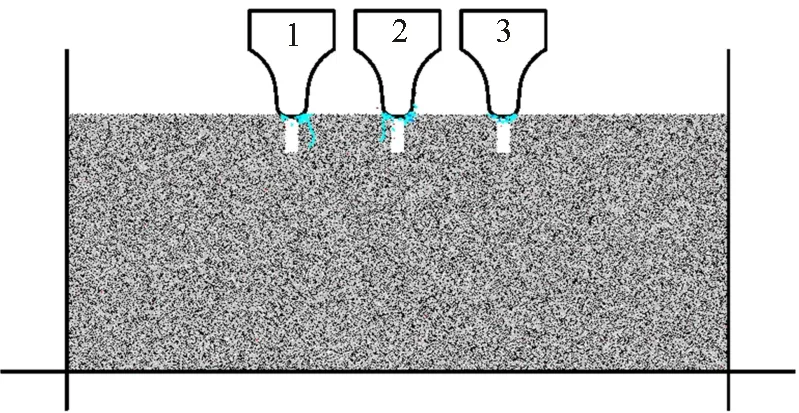
(e)槽宽10 mm的同缝切削

(f)滚刀破岩法向力图8 切削模式对破岩效果的影响 Fig.8 Influence of the indentation modes on rock fragmentation

针对图3所示的3种预切槽破岩模式,设定预切槽角度为0°,错缝切削模型的滚刀置于预切槽正中、刀槽间距为80 mm、预切槽宽度为2 mm、预切槽深度为30 mm;同缝切削模型的刀槽间距为80 mm、预切槽深度为30 mm、槽宽度分别为2、6和10 mm;混合切削模型的刀间距为80 mm、槽间距为160 mm。切削模式对破岩效果的影响如图8所示,错缝切削模式下岩石破碎充分、破岩效率高;对于同缝切削模式,滚刀破岩法向力明显小于错缝切削模式,且法向力随着槽宽的增大有减小趋势,因滚刀刃正下方是切槽空隙而无法建立密实核,且滚刀刃的接岩长度随槽宽增大而减小;对于同缝切削模式,刀下既无主裂纹也无侧向裂纹,仅有切槽口附近的少量岩石被压碎,岩石破碎效果很差;对于混合切削模式,位于切槽正上方的滚刀破岩法向力很小,其破岩效果不佳,位于切槽中部的滚刀破岩法向力很大,刀下产生了较长的主、侧向裂纹,但由于滚刀与切槽间距较大,无法贯通成碴。

上述分析说明,错缝切削是较为理想的预切槽辅助滚刀破岩模式,其特点是预切槽弱化围岩侧向约束和密实核驱动裂纹生长的双重机制组合破岩;同缝切削模式下由于刀下无法建立密实核而破岩效果差,混合切削模式中各把滚刀的破岩状态差别很大,两者均不是理想的预切槽辅助滚刀破岩模式。因此,后文均基于错缝切削模式开展研究。

3.3 预切槽位置对破岩效果的影响

基于错缝切削模式,设定预切槽角度为0°,预切槽宽度为2 mm,预切槽深度为30 mm,刀槽间距分别为120、110、100、90、80 mm,在各刀间距下设定2～3组偏置距离(滚刀与左侧预切槽的距离),建立14组模型。预切槽位置对破岩效果的影响如图9所示,当滚刀偏置时,滚刀两侧的岩石破碎效果差别很大,侧向裂纹与更近的左侧预切槽贯通,右侧的预切槽不起作用;当滚刀中置且刀槽间距较大时,虽然其与两侧预切槽距离相等,但两侧岩石破碎效果不同,这是由于侧向裂纹的生长方向具有一定的随机性;随着刀槽间距减小,各中置模型滚刀两侧的岩石破碎效果逐渐变得相似且均衡。以刀槽间距120 mm为例,各组滚刀偏置模型的侧向力和法向力如图9b～图9c所示,对于偏置20 mm模型,其破岩法向力为双峰形式,在第一个加载段,由于滚刀距左侧预切槽很近,岩石在较低的峰值载荷(3 MN/m)下发生破坏,随着滚刀继续贯入,碴块被滚刀推挤并抵住预切槽,使得滚刀下方再次形成密实核,由于滚刀距右侧预切槽距离较远,在第二加载段中侧向裂纹不能与右侧预切槽贯通;滚刀偏置40和60 mm(中置)模型的法向力相似,均为单峰形式,中置模型的破岩法向力峰值更大。偏置模型的破岩侧向力明显大于中置模型,因为偏置模型滚刀两侧岩石破坏效果不同。提取各组模拟的侧向力峰值如图9d所示,发现对于不同的刀槽间距,中置模型的滚刀侧向力峰值基本上均小于偏置模型。

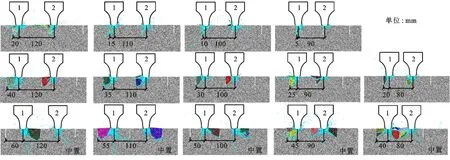
(a)不同预切槽位置下的岩石破碎效果

(b)刀槽间距120 mm的侧向力

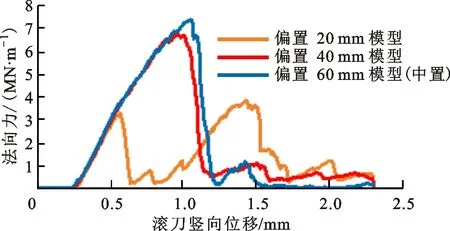
(c)刀槽间距120 mm的法向力

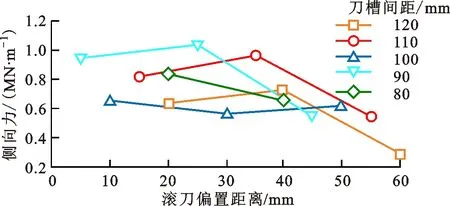
(d)各组模拟的侧向力峰值

上述分析说明,在适当的刀间距下,中置模型的滚刀两侧岩石破碎效果较为均衡、滚刀侧向力小,有利于提高破岩效率、保证破岩稳定、避免滚刀不良受力状态,因此建议滚刀置于相邻预切槽的中间位置。

3.4 槽间距对破岩效果的影响

窄直切槽、错缝切削、滚刀中置是理想的预切槽结构及排布方式,此时,相邻滚刀的间距和相邻预切槽的间距相等,统称为槽间距。设定预切槽宽度为2 mm、预切槽深度为30 mm、槽间距分别为60、65、70、75、80、85、90、95、100、105、110、115和120 mm,建立13组模型。槽间距对破岩效果的影响如图10所示,当槽间距小于80 mm时,两把滚刀下的侧向裂纹基本可以与预切槽顺利贯通,刀下岩石均衡、充分破碎;随着槽间距增大,刀下岩石不再充分破碎,尤其当槽间距大于100 mm,刀下侧向裂纹仅贯通至一侧预切槽,刀下密实核随后发生崩坏和应力释放,无法继续传递载荷从而驱动另一侧的侧向裂纹和预切槽相互贯通。不同槽间距下滚刀法向力如图10c所示,法向力峰值总体上随槽间距增大而增大,槽间距为120 mm模型的法向力峰值(7.4 MN/m)约是60 mm模型的法向力峰值(4.9 MN/m)的1.5倍,因为随着预切槽与滚刀距离变大,预切槽移除侧向约束而弱化围岩的效果逐渐变弱,因而滚刀破岩载荷增大。不同槽间距下的滚刀贯入比能如图10c所示,随着槽间距的增大,贯入比能总体上呈现双谷式变化,第1个波谷对应的槽间距为80 mm,第2个波谷对应的槽间距为115 mm;当槽间距由60 mm逐渐增大至80 mm,贯入比能逐渐减小,因为刀下岩石破碎较为充分,且岩碴量随刀间距增大而增大;当槽间距由80 mm逐渐增大至105 mm,贯入比能逐渐增大,因为刀下岩石的破碎开始变得不均衡、不充分,且破岩载荷逐渐增大;当槽间距进一步增大至115 mm时,贯入比能反而减小,因为刀下裂纹的生长存在一定的随机性,使得110与115 mm槽间距模型的滚刀1与两侧预切槽间均形成了大块状岩碴,使得总岩碴量显著增大;当槽间距为120 mm时,贯入比能再次增大,因为此时岩石破碎不充分、岩碴量少,且破岩载荷较大。

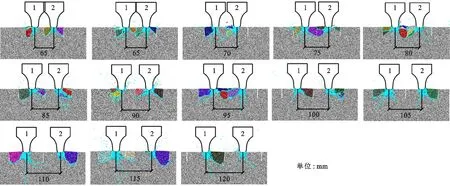
(a)不同槽间距下的岩石破碎效果

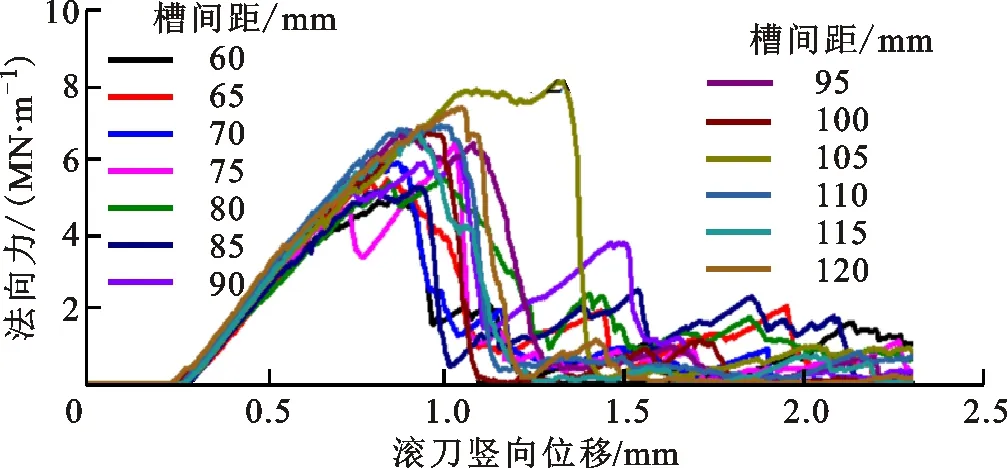
(b)不同槽间距下的刀1法向力

(c)不同槽间距下的滚刀贯入比能

上述分析说明,当槽间距介于60～105 mm时,破岩效率随着槽间距的增大而先增加后减小,当槽间距为80 mm时破岩效率最高;当槽间距取110～115 mm时,虽然破岩效率较高,但滚刀两侧的岩石破碎不均衡、不充分。因此,综合考虑破岩效率和岩石破碎均衡性,建议本文研究的花岗岩在“窄直切槽、错缝切削、滚刀中置”模式下的最优槽间距为80 mm。

4 结 论

本文针对预切槽辅助TBM滚刀破岩研究不足的现状、以及现有研究可靠性有待提高的问题,构建了基于优化泰森多边形算法的等效晶质岩石材料的颗粒簇离散元模型,研究了切槽角度、位置、间距等结构参数对破岩过程的影响,所得到的结论可为预切槽结构设计提供理论依据:

(1)本文的岩石材料建模方法可准确地表征岩石宏观物理性质,所构建的数值模型可较为可靠的模拟刀具贯入破岩过程,为TBM滚刀破岩机理研究提供了有效的手段;

(2)预切槽辅助下的滚刀破岩不再是相邻滚刀间侧向裂纹的联动贯通,而是侧向裂纹朝预切槽主动生长并贯通,其关键机制是预切槽弱化围岩和密实核传力驱动,可极大地提高硬岩破碎效率;

(3)基于切削模式、预切槽角度、位置与间距对破岩效率和岩石破碎效果影响规律的分析,确定“窄直切槽、错缝切削、滚刀中置”是最优的切槽结构及排布模式,建议预切槽开口角度为0°、错缝切削、滚刀置于相邻预切槽正中、最优预切槽间距为80 mm。