高体分SiC/Al复合材料微磨削表面粗糙度试验研究*

高 奇 郭光岩 荆小飞 李文博

(辽宁工业大学机械工程与自动化学院，辽宁 锦州 121000)

SiC/AI复合材料目前被广泛应用于汽车、航空航天、能源及医疗等重要工业部门，由于复合材料中含有高硬度或高刚性的细小颗粒，使得材料的硬度和耐磨性得到提高，但同时材料的加工难度也提高。为深入研究SiC/AI复合材料磨削[1]过程中，试验数据变化对表面粗糙度的影响，对其磨削后的各项数据进行试验研究。

国内外许多学者已经利用响应曲面法研究了大量具有代表性的可加工材料。姚倡锋等[2]对超高弹度Aermet100的磨削参数进行模型预测，通过对模型进行简化，建立了非线性回归方程，分析磨削参数对磨削结果的影响规律。刘伟等[3]对轴承钢GCr15的高速外圆磨削进行了研究。在多目标磨削参数的情况下，利用Design-Expert软件确定最佳回归方程模型，从而获得最佳结果，来表征磨削参数对磨削效果的影响。Krajnik P等[4]基于响应面方法对磨削因子进行设计，并建立二阶表面粗糙度模型。通过确定模型的结构和回归系数，演绎出准确模型。Zhou Ming等[5]利用超声振动辅助磨削SiC/Al复合材料，并建立力学模型，通过两组正交试验，得到了磨削力模型中的系数。在力学预测模型的基础上，预测了磨削力与工艺变量之间的关系。最后进行了两组单因素试验，验证了所提出的磨削力模型，实验结果与预测结果吻合较好。DU Jinguang等[6]结合金刚石颗粒对SiC颗粒的冲击和挤压效应，讨论了相应的去除方式及其机理，并通过多种方式去除SiC颗粒，得出结论：在材料去除过程中被剪切去除的颗粒越多，被破碎的颗粒越少，可以产生更好的加工表面。Li X K等[7]通过模拟砂轮的各个加工步骤，建立了虚拟单层CBN砂轮模型，使磨削过程中对单个晶粒材料去除模式成为可能。通过有限元模拟和响应面法(RSM)，研究了晶粒取向对CBN晶粒微观切削性能的影响。结果表明，单颗粒切削力对磨粒磨损状态和取向状态很敏感，有较好的取向条件使磨粒微切削获得最小切削力(40°～60°)。

本文采用响应曲面法，对SiC/AI2024复合材料进行磨削加工，然后通过Smartproof5激光共聚焦显微镜来测量材料的表面粗糙度Ra，在建模预测和试验结果相结合下，阐述主轴转速n、切削速度f和切削深度ap对表面粗糙度Ra的影响程度。

1 磨削试验

1.1 试件材料

工件材料为SiC/AI2024复合材料，其碳化硅增强颗粒所占体积比为60%，其硬度极高，加工难度大。试件已加工图及显微结构，如图1所示。试件为矩形块状，规格为40 mm×15 mm×10 mm。工件在室温(20 ℃)下，杨氏模量为206 GPa，剪切模量为83.1 GPa，密度为2.99 g/cm3，抗弯强度为513 MPa，泊松比为0.24。

1.2 试验设备

试验加工设备为北京精雕—睿雕Carver400GA数控机床，通过微径磨棒对SiC/AI2024进行槽磨[8]试验。磨棒规格：磨头直径1 mm，柄径3 mm。磨头材料为镀结金刚石。润滑装置为油水气三相节能微量润滑系统—KS-2107。磨削试验系统如图2所示，磨削过程：采用磨头直径为10 mm的磨棒对材料表面进行预加工，加工完成后进行换刀(磨头1 mm)，然后进行13组微磨削试验。磨削试验完成后，通过Smartproof5激光共聚焦显微镜测量已加工材料的表面粗糙度。

1.3 试验结果

本试验采用单行程磨棒端面磨削，利用Design-Expert软件中的Box-Behnken Design进行试验设计[9]。选取影响表面粗糙度Ra的主要影响因素：主轴转速n，进给速度f，切削深度ap。影响因素参数取值如表1所示，BBD试验设计为13组，试验方案与结果如表2所示。

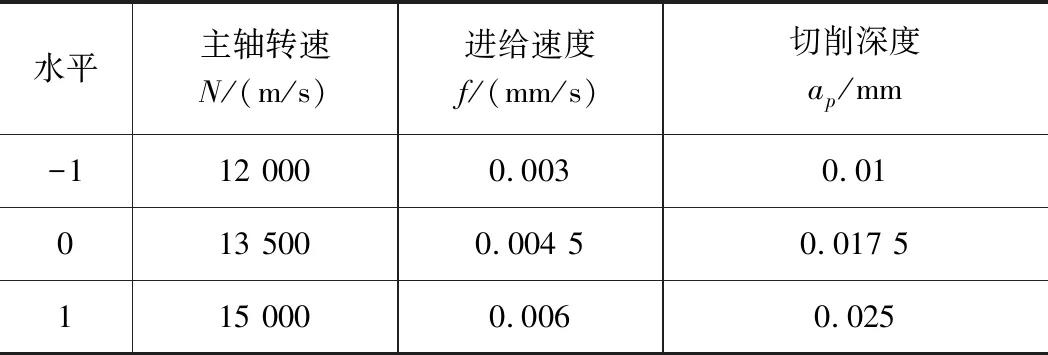
表1 影响因素取值

表2 试验参数与表面粗糙度的测量结果

2 回归方程的建立及分析

通过软件进行回归方程模型[10]的建立，模型如式(1)所示。

(1)

式中：xi表示自变量因子，y表示因变量因子，β0表示常数项，βi表示一次项相关系数，βij表示非线性相关参数，βii表示二次项相关系数，m表示自变量因子个数。

对表(2)中的试验参数与表面粗糙度的测量结果进行拟合，并建立预测模型，从而得到表面粗糙度与主轴转速、进给速度和切削深度之间的关系如(2)所示。

Ra=-4.74+7.45×10-4n+44.945f+

8.989ap-1.556×10-3nf-1.33×

10-4nap-88.889fapV-2.511E-

(2)

Ra=-4.74+7.45×10-4n+44.945f+

8.989ap+1.556×10-3nf-1.33×

10-4nap-88.889fap-2.511E-08n2

(3)

表3 模型分析

3 试验结果分析

3.1 响应曲线图分析

图3为ap=0.017 5 mm时，主轴转速和进给速度之间交互作用形成的响应曲面图[11]。当ap=0.017 5 mm时，Ra最小值为0.51 μm，最大值为0.734 μm。分析图3得出：(1)当进给速度保持不变时，表面粗糙度随着主轴转速的增大而增大，但增大趋势在12 000～15 000 r/min范围内逐渐减缓。(2)当主轴转速保持不变时，表面粗糙度随进给速度的增加，先减小后增大。(3)主轴转速对表面粗糙度的影响明显大于进给速度所造成的影响。

图4为确定ap=0.017 5 mm，n=15 000 r/min，f=0.006 m/min时，Ra为0.708 μm。图4中黑色部位为颗粒拔出，此部位约占总表面积的30%，被拔出颗粒大小形状不规则。极少数部分为浅黑色，此时表面粗糙度极大，在表面呈刺尖状突起，推测由于切屑粘结表面所致。灰白色部位占比较大，为刀具与材料磨削过程中相互挤压造成的。

图5为进给速度f=0.004 5 m/min时，主轴转速和切削深度之间交互作用下形成的响应曲面图。当f=0.004 5 m/min时，Ra最小值为0.518 μm，最大值为0.662 μm。分析图5得出：(1)当切削深度保持不变时，主轴转速的增大会导致材料表面粗糙度持续增大，但其影响程度逐渐减缓。(2)当主轴转速保持不变时，随切削深度的增大，表面粗糙度的值先增大后减小。(3)主轴转速对表面粗糙度的影响大于切削深度对表面粗糙度所造成的影响；切削深度在与主轴转速交互作用下对表面粗糙度影响极小。

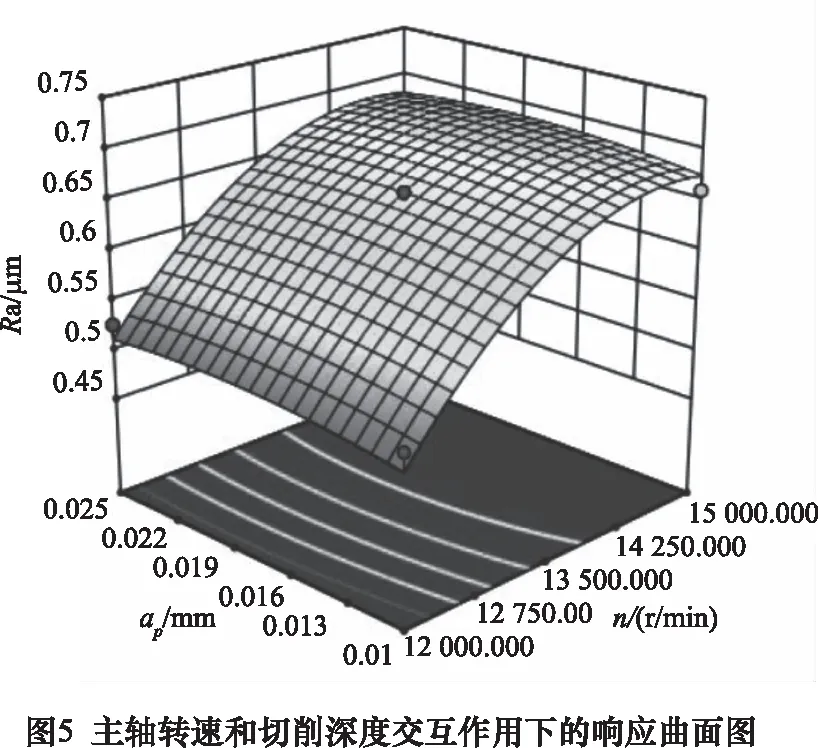
图6为确定f=0.004 5 m/min，n=15 000 r/min，ap=0.025 mm时，表面粗糙度Ra为0.662 μm。图6中黑色部位呈现大颗粒拔出或者数颗颗粒集体拔出，造成该部位凹陷程度加重。与图4相比，分析原因：在主轴转速不变的情况下，背吃刀量增加，进给量减小可能会造成颗粒被大幅度拔出。灰色部位呈凸起状，分析原因：被拔起的颗粒粘结在已加工材料表面；PCD刀具在高速磨削过程中倾向于经历金刚石-石墨相变，后者粘结在其表面。

图7为主轴转速n=13 500 r/min时，进给速度和切削深度之间交互作用形成的响应曲面图。当n=13 500 r/min时，Ra最小值为0.647 μm，最大值为0.681 μm。分析图7得出：(1)当切削深度保持不变时，表面粗糙度的值随着进给速度的增大，先减小后增大，但其影响程度较小。(2)当进给速度保持不变时，切削深度的增大会导致表面粗糙度先增大后减小，但变化幅度极小。(3)切削深度对表面粗糙度的影响程度大于进给速度对其造成的影响。

图8为确定n=13 500 r/min，f=0.004 5 m/min，ap=0.017 5 mm时，表面粗糙度为0.658 μm。与图4和图6相比，黑色部位占比明显增大，拔出颗粒大小较均匀，但颗粒成片拔出，较大地影响表面粗糙度的大小。分析原因：在三参数值同时降低后，使得磨削过程颗粒所受力较为均匀，导致颗粒拔出的规律性较好。灰色部位仍为尖刺状，所占比极少，预测为切屑粘结在表面所致。

3.2 残差图及预测值与试验值对比图分析

基于标准残差图[12]对结果的分析如图9所示，再利用Design-Expert软件对磨削试验结果进行分析并建立回归方程，绝大部分点均匀分布在直线上或者直线的两侧，可得试验数据而建立的回归方程可行性较好。

图10以实际值为横坐标，预测值为纵坐标，各数值点靠近直线分布或者位于直线之上。得出结论：预测值与试验值基本符合回归方程，模型拟合良好，试验结果较成功。

4 结语

(1)基于所有响应曲线图及等值线进行分析，得出结论，三因素对表面粗糙度的影响强弱为：主轴转速>切削深度>进给速度。

(2)在保证其他两个因素不变的情况下，得出如下结论：随切削深度的增大，表面粗糙度先增大后减小；随着进给速度的增大，表面粗糙度先减小后增大；随着主轴转速的增大，表面粗糙度也增大。

(3)建立的回归方程模型可以较为精准地反映以上3个因素对表面粗糙度的影响，且通过删除不显著项，建立的回归方程更具有说服力。