基于机器学习的露天矿排土场边坡稳定性预测

秦驰越 张文兴2

（1.包头铁道职业技术学院机械工程系，内蒙古包头，014060；2.北京科技大学机械工程学院，北京，100083）

排土场边坡是露天矿的一个组成部分，由破碎的覆盖层岩石材料组成。但随着作业深度的不断增加，排土场的陡度也随之增加，对工作环境造成了不稳定性威胁，可能导致矿山在人员、机械和材料方面的巨大损失［1-3］。因此，排土场边坡稳定性分析是非常重要的，有助于实现最有利的排土场边坡剖面设计。

排土场边坡稳定性分析方法大多采用安全系数FS作为评估边坡稳定性的指标［4］。极限平衡法是评估边坡FS的一种传统方法［5］，也是应用最为广泛的一种方法，但需要附加一定的假设和限制，导致准确度不高。目前，数值模拟已成为有效解决复杂边坡稳定问题的主流方法。许多研究者采用有限元方法对排土场边坡进行稳定性分析。例如，杨幼清等［6］采用二维有限元法模拟分析了5种不同工况下排土场边坡变形模式，准确性较高。但是，有限元方法需要利用多种岩土参数，如单位重量、黏聚力、内摩擦角等，并设定边界条件和荷载条件来模拟稳定性问题，因此实现过程较为复杂，且不具备可预测性，无法满足排土场剖面初期设计需求。

近年来，各种机器学习工具［7］层出不穷并成功应用于多个边坡工程项目，获得了较好的预测效果。例如，谢振华等［8］提出了基于BP神经网络的矿山排土场滑坡预警模型。人工神经网络（ANN）［9-10］和多元回归分析（MRA）［11-12］作为机器学习的2种经典模型，在解决各种预测问题中得到了广泛的应用。因此，本研究旨在利用上述2种模型来解决与覆盖层排土场相关的稳定性问题。使用Statistica10软件设计并构建了能够预测均匀排土场边坡FS的ANN模型和MRA模型。模型的输入变量为3个参数，输出值为预测的FS。将ANN模型和MRA模型的预测结果与数值模拟的计算结果进行了比较，验证了2种模型的准确性和实用性。

1 排土场边坡稳定性分析

1.1 排土场边坡

机械化露天采矿中使用拉铲挖掘机清除和搬运直接覆盖的岩石，大部分情况下在采场下盘设置排土场，形成独特的排土坡剖面。为提高排土场的稳定性，开采时在排土场一侧留有煤墙，以支撑排土场边坡，提高排土场容积。排土场边坡示意如图1所示。

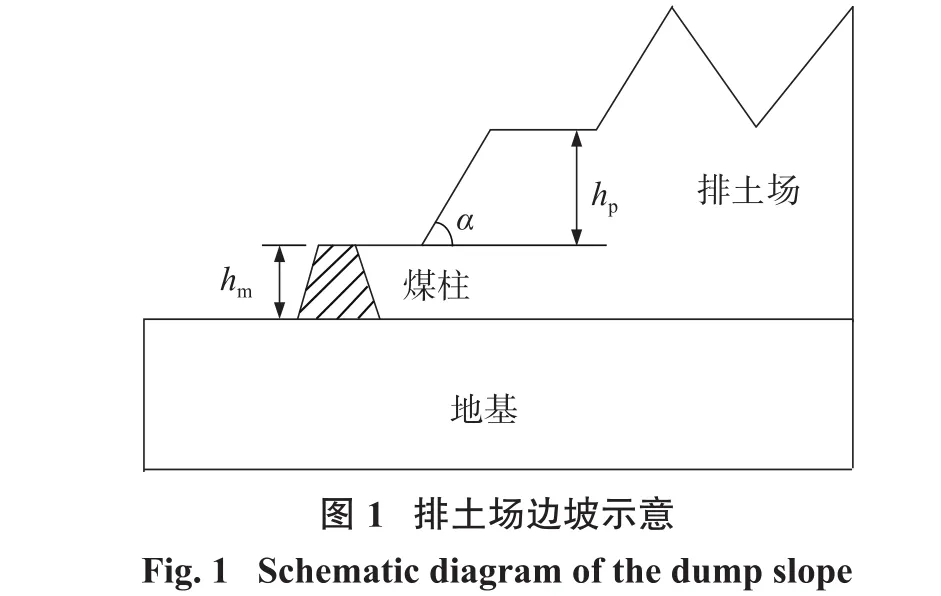
1.2 FS的计算

采用煤墙高度hm、排土场坡高hp和排土场坡角α3个几何参数进行模型设计：hm为10～20 m，间隔2 m；hp为25～45 m，间隔4 m；α为30°～50°，间隔5°。在本研究中，采用抗剪强度折减（SSR）有限元法来计算排土场模型的FS。在SSR技术中，实际强度特性（如内摩擦角和黏聚力）［13］的计算公式如下：

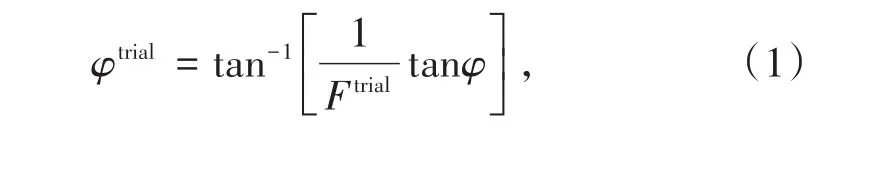
式中，φtrial为改变的内摩擦角；ctrial为各Ftrial值上改变的黏聚力；φ为实际内摩擦角；c为实际黏聚力值；Ftrial为排土场边坡模型临界失效的FS。

1.3 数据样本选取

机器学习模型的训练需要大量的数据，因此本研究在文献资料分析及现场勘探的基础上，采用有限元方法进行仿真获得了209个排土场模型的样本数据，并分为训练数据集和验证数据集两部分。在209个数据集中，70%（146个样本）被用作训练数据集，其余30%（63个样本）被用作验证数据集。训练和验证数据集的统计参数如表1所示。

2 机器学习模型设计

作为一种能够模拟人类大脑分析和处理信息的强力工具，ANN可以很容易地识别出自变量和目标变量之间存在的相关性，其神经网络体系结构描述了如何将输入变量转换为目标变量。ANN模型可以通过神经元的传递函数、训练算法和连接公式来描述。

2.1 ANN模型

将影响排土场边坡FS的3个几何参数：煤墙高度hm、排土场坡高hp和排土场坡角α作为输入变量，选择FS作为输出参数，建立了影响排土场边坡FS的ANN模型。

主要利用Statistica10软件来设计ANN模型。该软件由2种类型的神经网络结构组成：多层感知器（MLP）和径向基函数（RBF）。在本研究中，使用了MLP结构，因为它是目前最流行的前馈神经网络结构。神经网络体系结构包括2个重要工具:神经元的训练算法和激活函数。选择使用BFGS拟牛顿算法作为训练算法，该算法收敛速度快，具有智能搜索条件，需要的迭代次数较少。为了评估神经网络的性能，使用了平方和误差函数，该函数是训练数据集的实际输出和预测输出之间的差值的平方和。

在设计神经网络体系结构时，观察到单个隐藏层可以近似网络中的大部分函数，因此ANN模型中仅保留单个隐藏层。隐藏层和输出层使用的传递函数为sigmoidal函数。所设计的3层神经网络体系结构如图2所示。

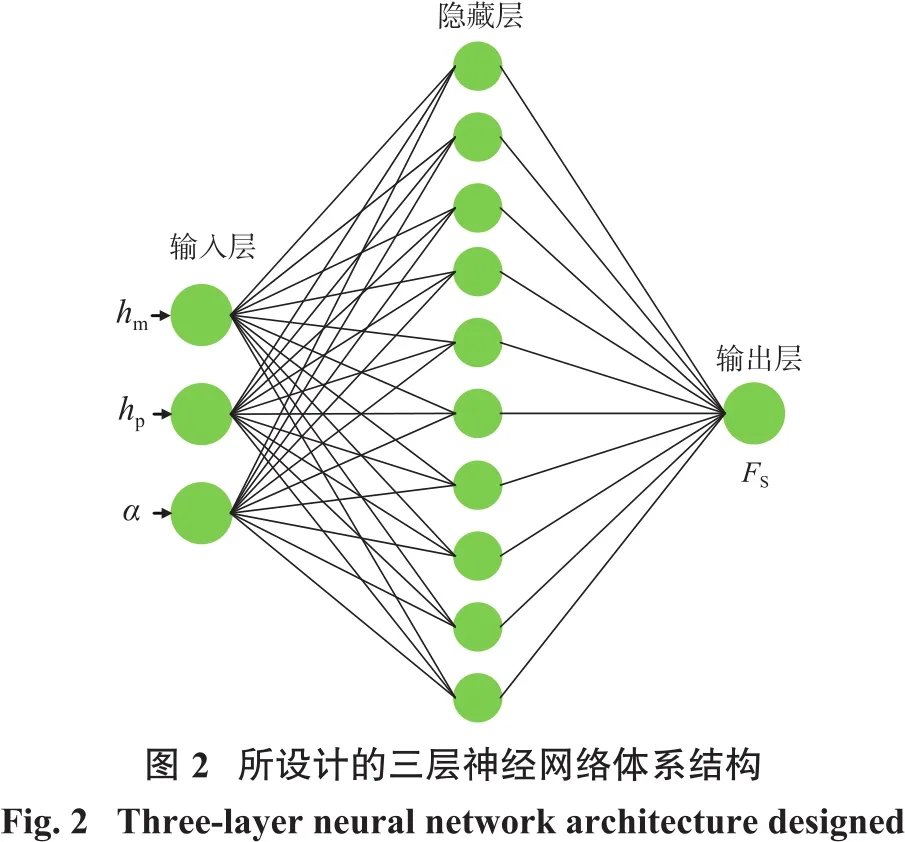
2.2 MRA模型

通常，回归分析的目的是预测各种输入和输出变量之间的相互关系特征。其中，多元回归分析（MRA）适用于多个输入变量，并可给出显示自变量与效标变量之间关系的最佳方程。MRA模型使用煤墙高度hm、排土场坡高hp和排土场坡角α作为自变量，FS作为输出变量。利用全部的209组仿真结果进行MRA模型的统计回归分析。MRA模型显示以下关系:

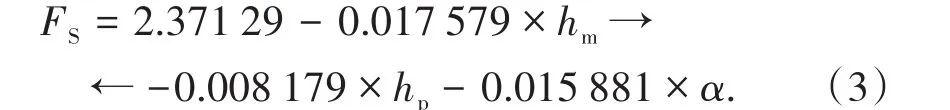
3 实验结果与分析

3.1 ANN模型的预测结果分析

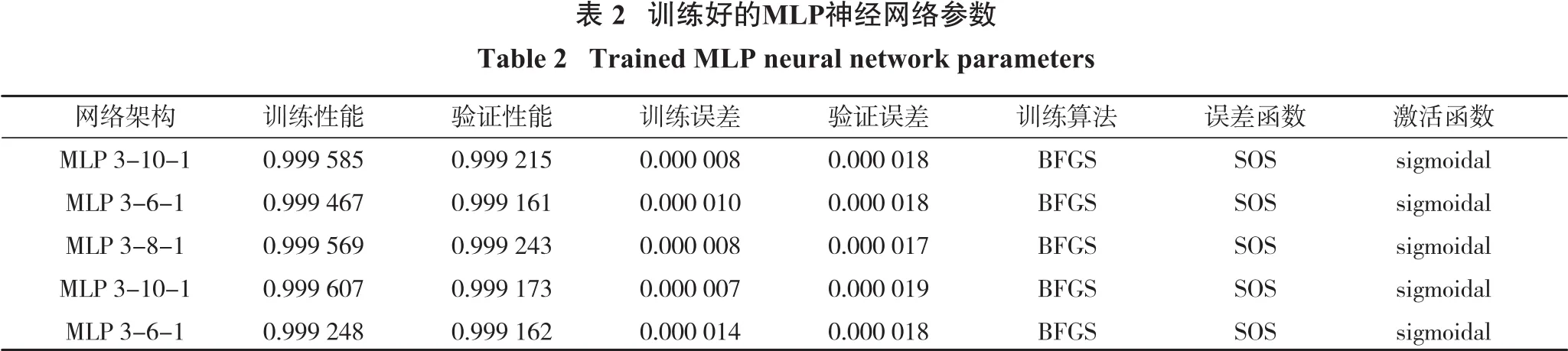
使用不同的MLP神经网络架构，对训练数据集进行多次训练后，得到了最好的5个结果，如表2所示。

从表2可见，MLP 3-10-1架构的ANN模型误差最小（0.000 007），确定系数最大（R2=0.999 6）。因此，最佳的ANN模型由1个包含10个神经元隐藏层组成。数值模拟计算的FS值与ANN模型预测值的比较如图3所示。

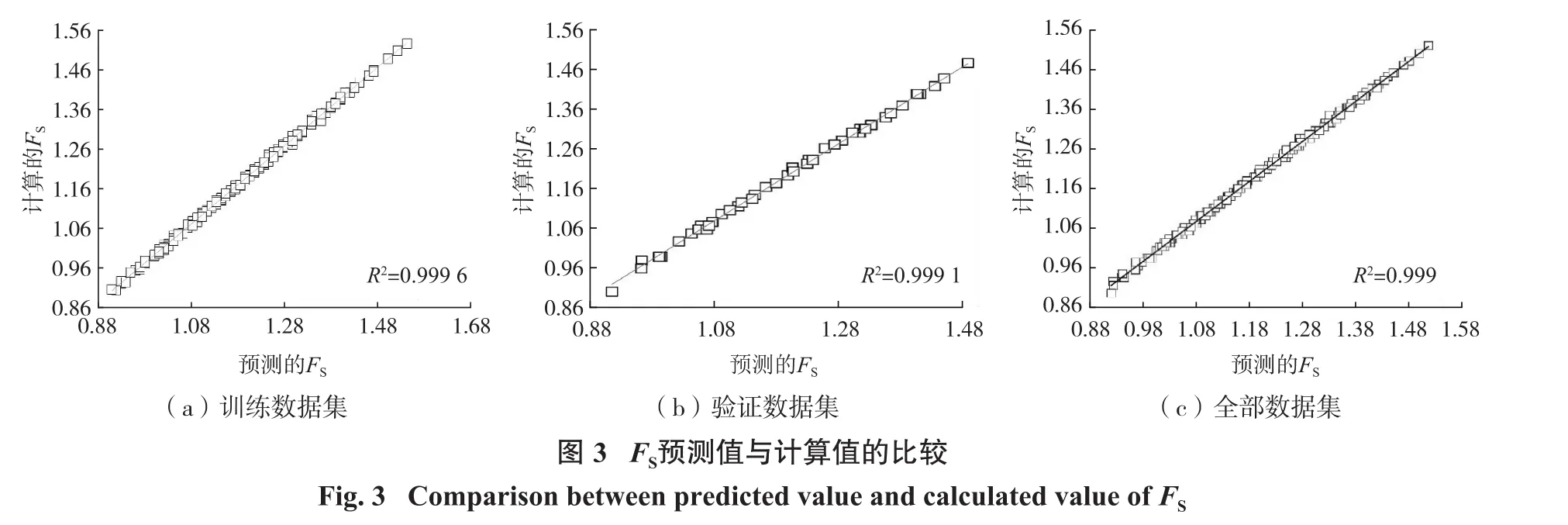
从图3中不难看出，计算的FS值与预测的FS值非常接近，R2值也非常接近于1。结果表明，在排土场剖面的初期设计阶段，利用训练好的ANN模型，可以很容易地预测出均质排土场的FS，且预测精度较高。

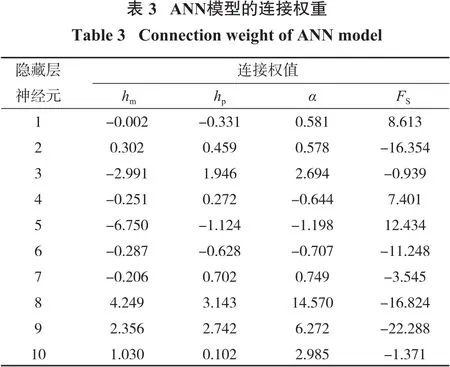
ANN模型的连接权重如表3所示。

确定所有3个输入参数对ANN模型输出的影响是至关重要的。因此，需要对输入变量的相对重要性进行计算，以便选择输入变量的最佳值，从而形成具有最大覆盖物容积量的安全排土场。利用基于神经网络权重矩阵的Garson方程对3个几何参数的相对重要性进行了评估。Garson方程如式（4）所示，方程中使用连接权值的绝对值。

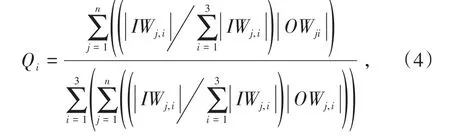
式中，i为输入变量；j为隐藏层内的神经元；Qi为第i个输入变量对输出的相对重要性；OWj,i为第j个神经元输出变量的权重；IWj,i为第j个神经元对隐藏层第i个输入变量的权重；n为神经元的数量。

3个输入变量对ANN模型输出的相对重要性如表4所示。

从表4中可以明显看出，α对排土场边坡稳定性的影响最大，相对重要性为49%。因此，α是这3个参数中影响最大的一个。

3.2 MRA模型的预测结果分析

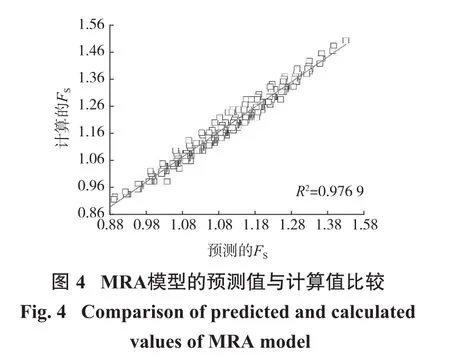
MRA模型同样具有3个输入参数hm、hp和α以及输出FS。MRA模型的预测值与计算值比较如图4所示。

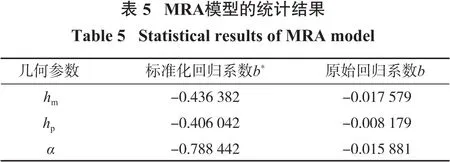
由图4得到，MRA模型的预测值与计算值非常接近，R2（0.976 9）的值接近于1。MRA模型的统计结果如表5所示。

表5中显示了标准化回归系数b*和“原始”或“非标准化”回归系数b。b*描述了自变量（hm、hp和α）对因变量（FS）的影响。几何参数α具有最高的b*系数值（绝对值），而hp具有最小的b*系数。因此，α是对排土场边坡FS影响最大的参数。综合考虑统计回归结果，可以确定MRA模型也可用于排土场剖面的初期设计。

3.3 MRA和ANN模型的性能对比

选取了确定系数R2、可解释方差VAF和均方根误差RMSE 3个指标［14-15］，对MRA模型和ANN模型的预测性能进行了评估比较。其中，VAF和RMSE的计算方式如下：

式中，y为计算值；yˆ为预测值；var为方差运算；N为模型样本个数。

VAF值越接近100，RMSE越接近0，则模型预测性能越好。MRA和ANN模型的性能指标如表6所示。

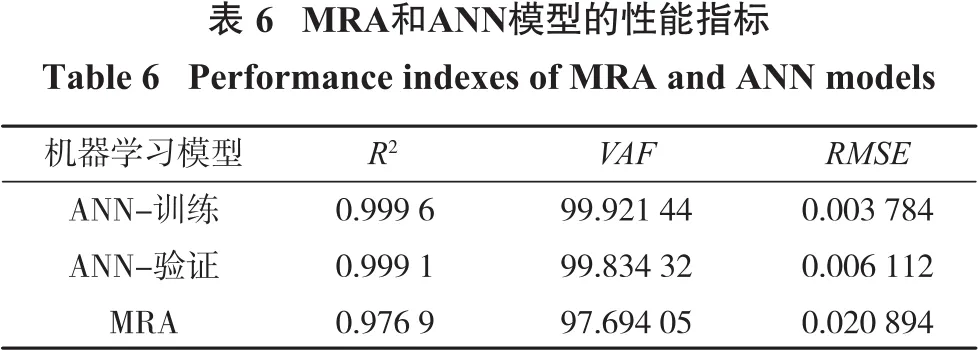
如表6所示，相对于MRA模型，ANN模型的VAF值较高且RMSE值较低，因此ANN模型的性能优于MRA模型。这是因为存在大量处理神经元的ANN模型具有更高的鲁棒性和容错性。

另一种直观比较MRA模型和ANN模型的方法是残差，主要显示预测值与计算值的偏差，即计算两者之间的差值。不同模型的残差变化情况如图5所示。

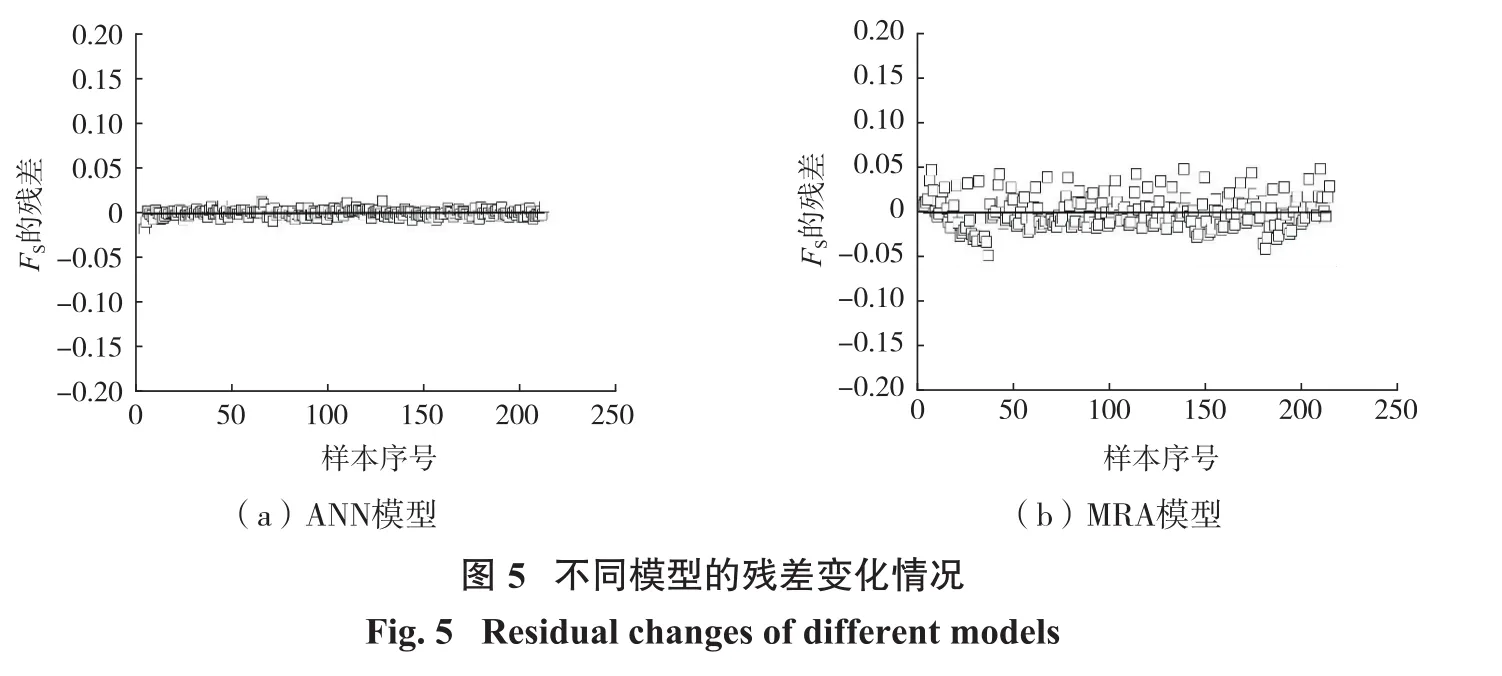
由图5可见，ANN模型的残差区间为−0.020～+0.015，明显小于MRA模型的残差区间−0.053～+0.054。这也证实了2种机器学习工具中，ANN模型相对于MRA模型具有更高的预测准确性。

4 结论

构建了可用于排土场边坡FS估算的ANN模型和MRA模型。模型设计所用的数据来源于209个排土场模型的有限元数值模拟结果。模型的输入变量为煤墙高度、排土场坡高和坡角3个几何参数，输出值为FS。通过实验得出如下结论：

（1）通过与数值模拟得到的FS值进行比较，验证了ANN模型和MRA模型的有效性，确定系数分别为0.999 6和0.976 9，符合预期。

（2）RMSE和VAF预测精度指标分析表明，MRA和ANN模型的RMSE分别为0.020 894和0.003 784，VAF值分别为97.69和99.92；

（3）残差分析表明，MRA模型和ANN模型的预测值变化范围分别为−0.053～+0.054和−0.020～+0.015，即ANN模型的残差变化较小。

（4）在3个输入几何参数中，相比重要性几乎相同的hm和hp，α参数的重要性最高。

后续将在ANN模型的激活函数和训练算法选择方面开展研究，以便寻找进一步提升其预测精度的方法。