基于非合作博弈的航班时刻优化研究
陈 彬, 翟文鹏
(中国民航大学空中交通管理学院, 天津 300300)
航班时刻是一个有限的资源,随着航班量的不断增加,航班延误出现得越来越频繁。因此如何高效地利用有限的航班时刻资源,减少航班延误这一问题亟待解决。为了从根本上解决该问题,就需要从航班时刻优化入手。目前解决航班时刻优化问题,建立优化模型时,大致都是以减少航班总延误时间,和航班最大调整量作为目标函数。
Corolli等[1]针对多机场网络,考虑机场容量的不确定性,以尽可能减少时间调整偏移和预期运行延误的总和为目的,提出了两阶段航班时刻优化模型;王倩等[2]为减少航班延误,并且降低航班调整对航空公司带来的影响,建立了机场群航班时刻优化及动态排队模型,并设计了改进的迭代寻优算法,以珠三角机场群为例对模型算法进行了验证;胡明华等[3]针对中国枢纽机场运营高峰时段分析了机场航班运行规律和存在问题,在保证正班航班运输需求的基础上提出基于历史数据的航班时刻优化模型,并改进匈牙利算法求解,以达到航空公司申请时刻调整量和航班地面等待时间整体最小的目标;汪梦蝶等[4]针对战略航班时刻优化问题,提出可接受调整量水平的概念,分析航班时刻表功效性与可接受性的权衡关系,建立双目标航班时刻优化模型, 基于ε-约束法的分步求解策略,采用带变异算子的改进粒子群算法进行求解。从中外研究现状可以看出,对于航班时刻的优化的结果好坏,大体以航班总延误和航班总调整量的最小值为依据。但是这两者在优化过程中,必然存在相互影响,相互制约。因此,拟从博弈论的角度对这两个目标进行分析,使航班总延误和航班总调整量在优化过程中达到一个均衡的状态,使整体得到一个最佳结果。
博弈论目前已经在分析航空公司之间的竞争,航空公司与高铁的竞争,航班时隙分配等问题中得到了运用[5-7]。在航班时刻多目标优化问题中,各个目标一般存在竞争关系,且每个目标都期望达到自己的最优值。那么可以运用博弈论对每个目标确定一个权重系数,解决已有多目标优化问题中,主次目标受到决策主观性的影响,最后依据纳什均衡给出每个目标的最优权重系数。
综上所述,将航班总延误时间和航班总调整量作为目标,然后通过基于零和博弈的多目标线性加权法得到最佳权重系数,构建数学模型,并采用萤火虫算法(FA)求解。以杭州萧山国际机场为例,验证该模型对航班时刻优化结果的有效性。
1 机场航班时刻优化模型
1.1 基于零和博弈的多目标线性加权法
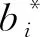
为解决原问题中各个目标函数的量纲存在差异,需要进行归一化处理,即
(1)

(2)
式(2)中:A′为成本。参与方1期望A′达到最大,而参与方2就是期望A′达到最小,因此零和博弈模型为
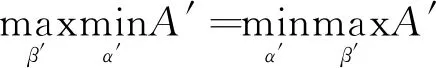
(3)
(4)
(5)
求解该模型等价于求解两个线性规划问题:
(6)
(7)
(8)
(9)
式中:wi为概率α′i与支付A′的比值;vj为概率β′j与支付A′的比值。
求解上述两个规划问题得到最优支付为
(10)
得纳什均衡解为
(11)
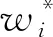
依据纳什均衡解可以得出原问题各个目标的权重系数:
(12)
式(12)中:aii为选择ai和bi策略的支付。
最后将上述得到的权重系数应用的原问题,将多目标转换为单目标进行求解,即
(13)
式(13)中:A为目标函数的优化结果。
1.2 目标函数
将航班总延误时间和总调整量两个目标转换为单目标作为一个整体,使此整体达到最小化,建立如下目标函数:
(14)
式(14)中:f∈F,集合F={1,2,3,…,n}为航班的集合;t∈T,集合T={1,2,3,…,m}为时间片集合,每个时间片长度取5 min;α1、α2分别为航班总延误时间和航班总调整量基于零和博弈的权重系数;wft为在t时间片的航班f的延误时间;Vft为在t时间片的航班f的调整量;
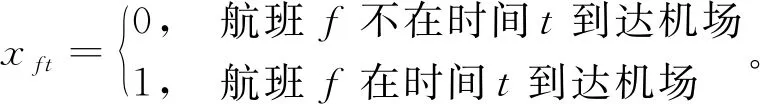
1.3 约束条件
(1)航班的唯一性。一个航班仅分配一个时间片。
(15)
(2)机场进场容量限制。机场运行时间t内,可允许飞机降落的架次受到容量的限制。
(16)
(17)
(18)
式中:a5、a15、a60分别为机场在5、15、60 min内的进场航班容量限制;k={1,2,3,…,190},q={1,2,3,…,181}。
(3)时间片调整量限制。一个航班的时间片调整应该在原时刻基础上的一定范围之内。
(19)
式(19)中:p为在时间片t的航班f的时间片调整量不超过p。
2 萤火虫算法
萤火虫算法(FA)是一种启发式算法,它将空间中各个解看成萤火虫,利用发光强的个体会吸引发光低的个体的特性。当在发光弱的个体向发光强的个体移动的过程中,更新自身的位置,获得新解,如此往复不断迭代,当最后达到迭代限制或者达到精度要求,便完成寻优过程,将得到的最优位置作为最优解[9]。与遗传算法相比,萤火虫算法有计算精度更高、收敛速度更快,并且参数少,易于实现的特点[10]。
建立萤火虫算法需要满足以下条件:①设所有萤火虫性别相同且相互吸引;②吸引度只与发光强弱和间隔距离有关,发光强个体吸引发光弱个体,吸引度与距离成反比,发光强的个体做随机运动;③目标函数决定个体发光强弱,并且成比例关系。
因此,寻优过程中萤火虫有两个重要参数,分别是发光亮度和相互吸引度。
设计算法如下:
(1)初始化。设置萤火虫的数目为n个,每一个萤火虫的所在位置表示一个解,即航班时刻表,解的维数为d,即一个航班时刻表所包含的航班架次数;最大吸引度为β0,光强吸收系数为γ,步长因子为α,迭代次数为t,最大迭代次数为m。
(2)随机生成萤火虫的位置,计算萤火虫的目标函数值作为各自最大发光亮度I0。
(3)计算萤火虫之间的相对亮度I和吸引度β。根据这两个参数决定萤火虫移动的方向和快慢。涉及的公式为
(20)
I=I0e-γrij
(21)
(22)
式中:Xi、Xj分别为萤火虫i、j的位置坐标;Xik、Xjk分别为萤火虫i、j坐标向量第k个坐标位置;e为自然常数。
(4)位置更新。对萤火虫所在位置进行更新,向亮度最高的萤火虫移动。
(23)
式(23)中:rand为在[0,1]上服从均匀分布的随机数。
(5)对位置更新后的萤火虫重新计算亮度。
(6)当得到的最优解达到所需要的精度或者最大迭代次数,则算法停止并输出最优解和最优值;否则迭代次数加1,转步骤(3),继续进行搜索。基于萤火虫算法的航班时刻优化流程图如图1所示。
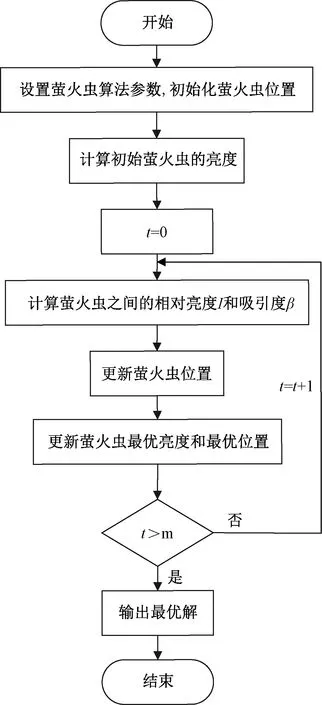
图1 算法流程图
3 算例分析
选取杭州萧山国际机场2020-11-16当天8:00—24:00的航班时刻,该时间段内共降落航班321架次。分别以5 min、15 min、1 h作为时间片,对航班的进场架次在时间上进行合理的安排。时间片长度设置为5 min时,只有4个时间片降落航班架次为4架次,不超过3架次的时间片占97.92%,故设置机场5 min容量为3架次;时间片长度设置为15 min时,只有5个时间片降落航班架次为8架次,不超过7架次的时间片占92.19%,故设置机场15 min容量为7架次;时间片长度设置为1 h时,只有1个时间片降落航班架次为28架次,不超过24架次的时间片占93.75%,故设置机场1 h容量为24架次。并在优化过程中设置最小调整量为5 min,最大调整量为15 min。

表1 航班时刻优化问题零和博弈的支付矩阵
由式(3)建立的零和博弈问题,可求得纳什均衡解α1=0.13,α2=0.87。由图2看出,在15∶00至16∶00落地航班量为24架次,航班量较大,所以选择在这一个小时的情况下,多目标优化结果和基于零和博弈模型的优化结果进行对比。
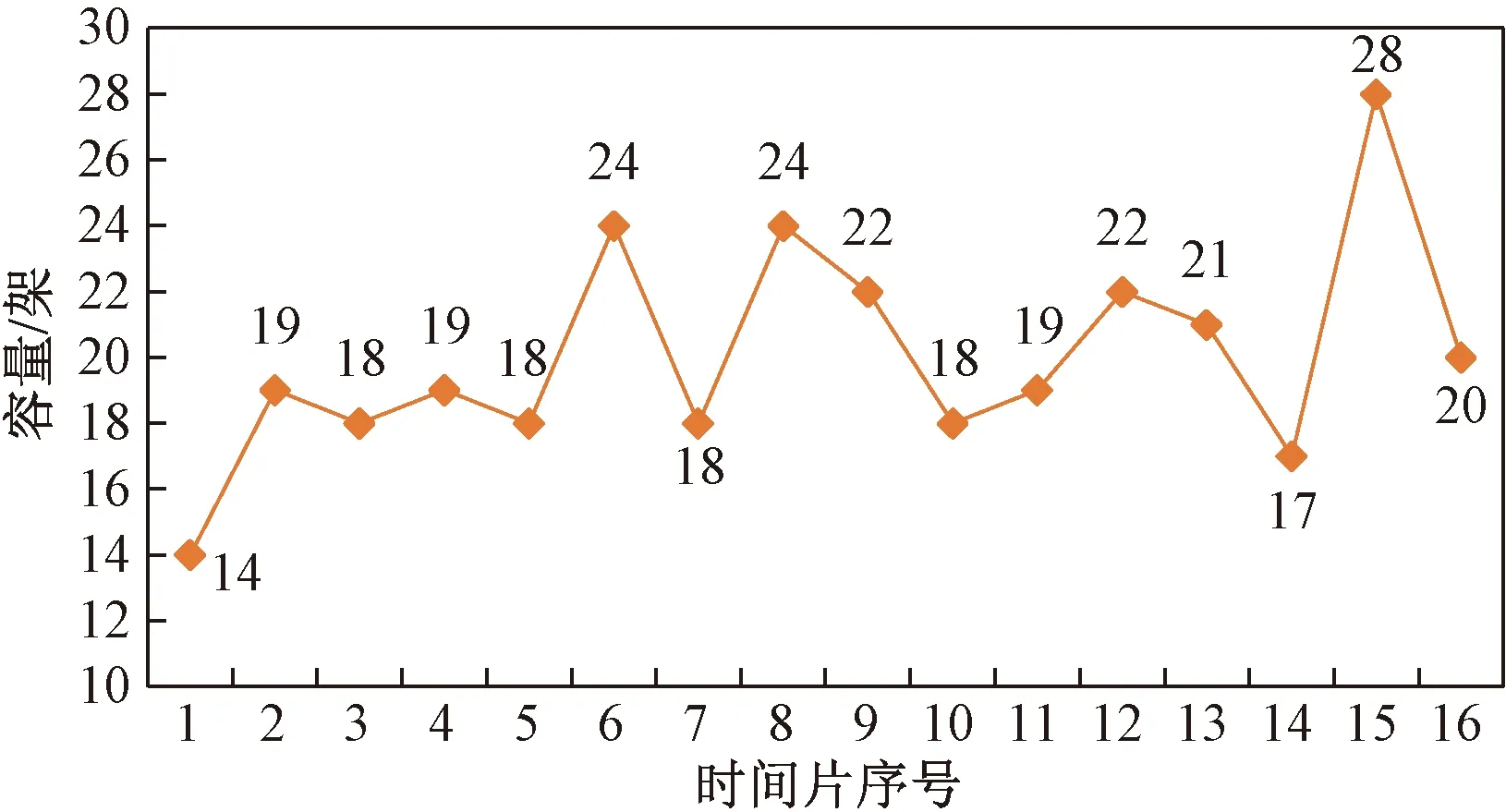
图2 每小时航班降落架次
图3(a)是主要考虑航班总延误的多目标优化后航班时刻表,和基于零和博弈模型优化后的航班时刻表的对比,可以看出两者在优化后整体相对重合,但是多目标优化的调整量会相对较大;图3(b)是主要考虑航班总调整量的多目标优化后航班时刻表,和基于零和博弈模型优化后的航班时刻表的对比,可以看出两者调整幅度比较相近,但是多目标优化的曲线略高于零和博弈模型的优化,即延误较高;图3(c)是基于零和博弈模型优化后的航班时刻表和实际航班时刻表的对比,可以看出优化后的航班时刻表曲线比实际的要低,即延误有减少,且幅度较低,即调整量少。
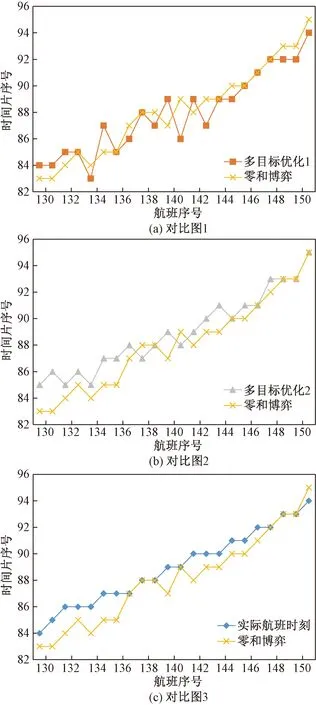
图3 航班时刻优化对比图
表2给出了不同优化方式下的结果。单目标优化指仅以航班总延误或航班总调整量为目标;多目标优化指线以其中一个目标为主目标,而将另外一个目标作为约束条件再进行优化;零和博弈指本文使用零和博弈模型确定权重,再用萤火虫给算法进行优化。可以看出基于零和博弈模型的优化得出的结果可以更好地均衡航班总延误时间和航班总调整量。
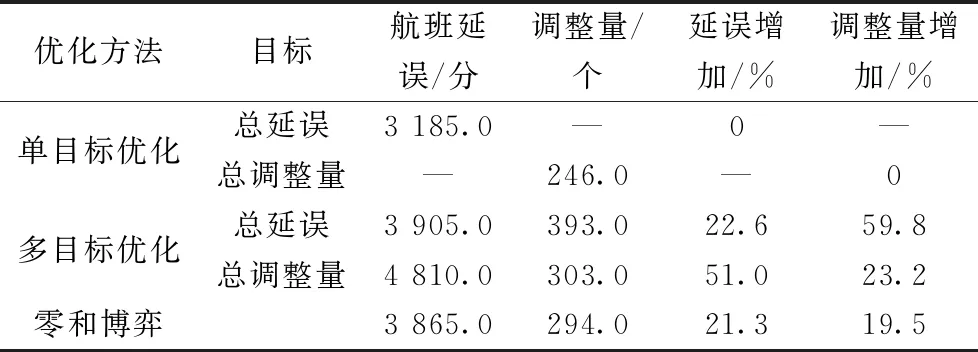
表2 不同优化方法结果
在图4和图5中,时间片长度分别为15 min和60 min的情况下,对比优化前的机场容量和零和博弈下优化后的机场容量,优化后均未超出机场容量限制,并且每个时间片的航班分布更加均匀。由表3可知,机场整体延误情况,也得到了有效的改善,航班准点率提高了9.7%。
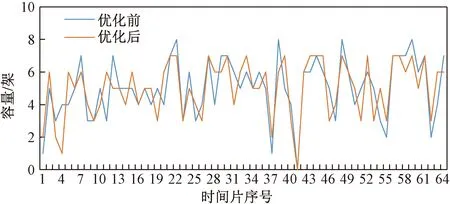
图4 15 min优化前后航班量对比
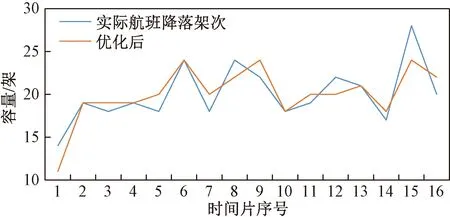
图5 60 min优化前后航班量对比

表3 航班时刻优化前后延误情况对比
4 结论
(1)相较于以往主观或客观定义权重的方式,另两个目标之间为使各自效益最大化进行博弈,得出纳什均衡策略下的最佳权重系数,可以使航班总延误和航班总调整量均达到相对满意的结果。
(2)与传统的不同优化方法之间相互比较,可以看出,基于零和博弈的航班时刻优化模型在优化上,使航班总延误相比于单目标优化只增加21.3%,航班总调整只增加19.5%,即整体优化效果要高于传统的多目标优化。
(3)使用零和博弈的航班时刻优化模型进行优化的结果与实际航班数据进行对比,可以看出航班量分布更加均匀,在最大航班量限制以下。同时航班整体延误得到了改善。但随着航班量的增加,通过调整航班时刻,很难将机场的延误有效地降低,所以两者之间的博弈关系仍然需要进一步讨论。

