STEM教育能提高中小学生学业成就吗？——基于国内外31项实证研究的元分析

李 珍 李小红 陈 晨 王 杉 刘 拓

(1.北京师范大学 中国基础教育质量监测协同创新中心，北京 100875；2.教育部人文社会科学重点研究基地天津师范大学心理与行为研究院，天津 300387；3.天津师范大学 心理学部，天津 300387)

一、引言

近年来，STEM教育在世界范围内兴起，并迅速成为各国广泛关注的新型教育范式。(1)Ye-Ping Li et al.,“Learning about Research and Readership Development in STEM Education: a Systematic Analysis of the Journal’s Publications from 2014 to 2018,”International Journal of STEM Education 6,no.1(2019): 1-8；Ye-Ping Li et al.,“Research and Trends in STEM Education: a Systematic Review of Journal Publications,”International Journal of STEM Education 7,no.1(2020): 212-242.STEM教育强调科学、技术、工程和数学的跨学科整合，重视培养学生实践能力，以能够运用多学科知识理解问题、解决现实问题为核心要义。(2)T.J.Kennedy and Michael R.L.Odell,“Engaging Students in STEM Education,”Science Education International 25,no.3(2014): 246-258；杨开城等.STEM教育的困境及出路[J]．现代远程教育研究，2020，(2)：20-28.然而，学界关于STEM教育效果的评价褒贬不一，对其影响因素的探讨也尚未达成共识。(3)Bevo Wahono et al.,“Evidence of STEM Enactment Effectiveness in Asian Student Learning Outcomes, ”International Journal of STEM Education 7,no.1(2020): 1-18.学业成就(academic achievement)是衡量教育过程有效性的重要指标(4)胡咏梅，元静．学校投入与家庭投入哪个更重要？——回应由《科尔曼报告》引起的关于学校与家庭作用之争[J]．华东师范大学学报(教育科学版)，2021，(1)：1-25.，因此，研究者以学业成就为标准进行了大量实证研究，以验证STEM教育的效果。但是，这些研究所采用的研究设计和效应量计算指标各不相同，因此无法进行结果的直接比较，以判断哪种研究结果更具有参考价值。若能采用恰当的方法将不同的研究结果放在同一量尺上进行比较，再经过整合得出相对客观的结论，将有助于厘清STEM教育对学业成就的真实作用。(5)Jeong Heisawn et al.,“Ten Years of Computer-Supported Collaborative Learning: a Meta-Analysis of CSCL in STEM Education during 2005-2014,”Educational Research Review 28,(2019): 1-17.

元分析正是这样一种方法，它能够对多项实证研究进行二次分析，得出一般性的结论。该方法由格拉斯(Glass)于1977年提出，是一种首先应用于临床心理学的定量文献分析法。(6)Mark W.Lipsey and David B.Wilson, Practical Meta-Analysis(Thousand Oaks：Sage Publication, 2001), 1-23.其具体步骤如下：先以一定的规则筛选文献，再用同一效应量计算指标计算单个研究的效应量，最后将单个效应量通过加权平均计算出合并效应量，即可得到该研究主题下多项研究的预测变量有效性程度。(7)马志强等．跨学科协作学习何以有效——STEM教育中CSCL应用效果的元分析[J]．现代远程教育研究，2021，(1)：97-104.元分析区别于传统主观性较强的文献分析法，具有如下两点优势：一是研究者在难以直接获得研究数据的情况下，也可以对存有争议的实证研究结果进行二次分析。二是可以相对客观地得出一般性的结论以解决研究争议，并深入探究引起研究结果差异的原因。

在元分析的研究过程中，首要任务就是确定研究对象。只有确定了研究对象，才能限定文献检索和筛选的范围。STEM教育的受众群体极为广泛，覆盖了K-12乃至大学和研究生的各个阶段。本研究的研究内容是STEM教育对学业成就的影响，并将标准化测验成绩作为学业成就的评价指标。而幼儿阶段的评价方式并非标准化考试，所以不将学龄前儿童纳入研究。同时大学和研究生阶段的学习内容和考评方式更加多元，难以横向比较。综合来看，小学、初中和高中阶段的学习特征相近，具备较大的可比性和规律性。因此，本研究拟运用元分析，探究STEM教育对中小学生学业成就的影响及其影响机制。

二、文献综述

世界各国就STEM教育对中小学生学业成就的影响问题进行了深入研究。其中，以美国为首的发达国家(地区)对STEM教育研究较早，在STEM教育对学业成就的影响方面积累了许多实证研究经验，但尚未形成一致的结论。(8)*表示同时被纳入元分析的实证研究。Pierre Dillenbourg et al.,“The Evolution of Research on Computer-Supported Collaborative Learning,”in Technology-Enhanced Learning, ed. Nicolas Balacheff et al.(Netherland：Springer, 2009), 3-19.部分研究者认为STEM教育能够对学生学业成就产生显著正向影响。李艳燕等发现，与传统教育相比，STEM教育能够显著提升小学生的问题解决能力(R=0.400)(9)Yan-Yan Li et al.,“The Effect on Pupils’ Science Performance and Problem-Solving Ability through Lego: an Engineering Design-Based Modeling Approach,”Journal of Educational Technology & Society 19, no.3(2016): 143-156.，史蒂文(Steven)的研究也表明，STEM教育有助于提高小学科学成绩(效应量偏η2=0.752)(10)Steven J.Seage,“The Effects of 5E Blended Learning on the STEM Achievement of Diverse Students” (PhD diss., Barry University, 2020), 17-20.。春蓬(Chumpon)等指出，在实施STEM教育后，学生物理成绩明显提高，效应量R2=0.26。(11)Chumpon Chanthala et al.,“Affecting the Activity-Based on Learning Approaching Management through the STEM Education Instructional Method for Fostering the Creative Thinking Abilities, Learning Achievements and Environmental Perceptions in Physics Laboratory Classes of Secondary Students at the 10th Grade Level,”European Journal of Education Studies 3,no.5(2017): 94-122.类似的研究还有许多(12)Holly Dalby,“STEM Integration and its Impact on Student Learning: a Mixed Methods Study”(EdD diss., Northcentral University, 2020), 67-94；Carol C.Waters,“Exploring K-5 STEM Educators’ Perceptions of a Successful STEM Elementary School” (EdD diss., University of Houston Clear Lake, 2018), 63-77.，这些研究都发现，与未接受STEM教育的学生相比，接受STEM教育的学生学业成就显著更高。然而，也有研究认为，STEM教育未能对学业成就产生作用，或是其效果明显差于传统教育。米歇尔(Michelle)采用准实验研究发现，STEM课程不会对中学生学业成绩产生显著影响(p>0.01)。(13)Michelle Renee Hammonds,“Science, Technology, Engineering, and Mathematics (STEM) Curriculum and Standardized Test Scores in Middle School Students”(M.Ed diss., University of Houston, 2012), 32-38.杰米(Jamie)的研究也表明，在前测成绩相同的情况下，与接受STEM教育的学生相比，接受传统教育的学生数学和科学成绩显著更高(p<0.001)(14)Jamie Smith James,“Science, Technology, Engineering, and Mathematics (STEM) Curriculum and Seventh Grade Mathematics and Science Achievement”(EdD diss., Grand Canyon University, 2014), 93-96.。而迪恩(Dean)则发现STEM教育与科学成就之间存在显著的负相关关系。(15)Dean Cairns and Shaljan Areepattamannil,“Exploring the Relations of Inquiry-Based Teaching to Science Achievement and Dispositions in 54 Countries,”Research in Science Education 49,no.1(2019)：1-23.

由此可见，学界对STEM教育与学业成就之间的关系探讨仍存在争议。这或许与STEM教育对学业成就的影响会受到其他因素的制约有关。已有研究多从课堂实施质量、非智力因素、性别差异等方面来解释STEM教育对学业成就的影响。乔纳森(Jonathan)等人发现是否接受长期、高效的STEM课程对STEM教育与学业成就的关系具有显著影响。(16)Jonathan Wai et al.,“Accomplishment in Science, Technology, Engineering, and Mathematics (STEM) and its Relation to STEM Educational Dose: A 25-Year Longitudinal Study,”Journal of Educational Psychology 102, no.4(2010): 860-871.马克(Mark)论证了STEM兴趣和态度在STEM教育与学业成就关系中的调节作用，并指出男女生在STEM学习态度上存在着差异。(17)Mark Patrick Mahoney,“Students' Attitudes toward STEM: Development of an Instrument for High School STEM-Based Programs,”Journal of Technology Studies 36,no.1(2010): 24-34.同样，敏(Myint)的研究表明男女生的空间能力差异会导致STEM教育对学业成就影响的不同。(18)Myint Swe Khine, Visual-Spatial Ability in STEM Education(Berlin: Springer International Publication, 2016):195-224.而吕伟妮(2020)的研究表明男女生学习STEM课程的能力差异是由性别刻板印象所致。(19)吕伟妮．中学生STEM学业成就差异的性别作用机理研究[D].山东：青岛大学教育系师范学院，2020.综上所述，学界对于STEM教育与学业成就的关系及影响这一关系的调节变量的解读各不相同。

近年来，为了寻求STEM教育与中小学生学业成就关系的一致性结论，国内外研究者尝试用元分析方法归纳整合不同实证研究结果(20)许静等．国外中小学STEM教学影响学生学习效果的元分析[J]．当代教育论坛，2020，(5)：89-97；马志强等．跨学科协作学习何以有效——STEM教育中CSCL应用效果的元分析[J]．现代远程教育研究，2021，(1)：97-104；Veli Batdi,“The Success of Students Using the Conceptual Map Technique and the Traditional Learning Method, its Effect on the Persistence and Attitudes of the Knowledge: a Meta-Analysis Study,”Dumlupinar University Journal of Social Sciences 42,no.2(2015): 93-102；Nam Ju Kim et al.,“Effectiveness of Computer-Based Scaffolding in the Context of Problem-Based Learning for STEM Education: Bayesian Meta-Analysis,”Educational Psychology Review 30, no.2(2018): 397-429.，但已有研究都在不同程度上存在一定的问题，一是纳入文献的筛选规则不明确，无法确定纳入文献与研究内容的适切性。二是所研究的STEM教育方法较为单一，使得研究结果的可推广性较差。因此，本研究在前人研究的基础上，拟通过科学的元分析方法解决如下两个问题：(1)STEM教育是否有助于提升中小学生的学业成就，其提升程度有多大？(2)哪些调节变量影响了STEM教育对中小学生学业成就的影响？

三、研究设计

本研究采用元分析方法进行研究。其研究步骤主要包括：文献检索、文献纳入标准的制定、文献筛选、文献编码、编码准确性评估、效应量的计算与合并、异质性分析以及发表偏倚检验。(21)Michael Borenstein et al., Introduction to Meta-Analysis(New Jersey: John Wiley & Sons, 2009), 1-37.本研究采用R 4.0.4软件中的metafor、meta、dmetar、dplyr、esc统计包进行数据分析。

(一)文献检索

元分析研究所纳入的文献应尽量全面，文献来源应尽可能广泛。为此，本研究依据布尔检索规则在Web of Science Core Collection、ERIC(EBSCO)、ProQuest Dissertations & Theses (PQDT)、Taylor & Francis Online、Wiley Online Library、Science Direct这6个教育学领域常用数据库以 (“STEM education”OR“STEM” OR “integrated STEM education”) AND (“student achievement”OR“student performance”OR“teaching effect”OR“teaching effectiveness”OR“teaching role”OR“teaching impact” OR“ academic achievement”OR“learning outcomes” OR“education evaluation”)为检索式进行高级检索，在Google Scholar进行精细检索，并在中国知网、万方搜索以关键词“STEM教育”、“整合STEM”并含“学业成就、评估、学业表现”，搜索发表于2002-2021年间(22)根据WoS核心数据库统计显示，真正开始对STEM教育进行研究是以2002年伊莱恩·西摩(Elaine Seymour)在《科学教育》期刊上发表了一篇题为《美国本科科学、数学、工程和科技教育变革过程的跟踪》的文章为标志。的文献，语种分别为英文和中文。首次检索获得的文献数量为19627篇。

(二)文献纳入标准制定

在制定元分析文献准入规则时，应严格按照研究目的、研究内容和统计需要来确定，避免个人主观意愿。结合本研究主题，确定纳入文献需满足如下4个条件：

1.研究所使用语言为中文或英文，发表于2002-2021年间，文献类型为期刊文献或硕博学位论文。

2.研究内容为STEM教育对中小学生学业成就的影响，不包含学前教育、特殊教育、职业教育等，不涉及对学生思维水平、非认知能力等的影响。

3.研究类型为实证研究，排除定性研究，实证研究的研究设计为相关研究、因果推断研究或实验研究，实验研究为随机实验或准实验设计，均设置实验组(STEM教育)和对照组(传统教育)，便于比较STEM教育和传统教育对学业成就的影响。

4.研究应报告均值、标准差、样本量或t值、F值、效应量等统计信息，确保能计算或转换出单个效应量和合并效应量。

(三)文献筛选

根据上述文献准入规则，首先通过标题进行第一次文献筛选得到1696篇相关文献。然后通过阅读摘要排除明显不符合规则的文献，剩余60篇。最后进行全文阅读筛选，得到31篇符合纳入标准的文献，获得有效效应量42个(23)部分文献有多个研究，得到多个有效效应值。，总样本量为12332。筛选过程如图1：

(四)文献编码

确定原始文献后，对原始文献进行编码，生成数据文件，以便进行后续各项指标的计算。参照马克(Mark)和大卫(David)提出的规则，文献编码至少需要包含作者、出版年份、研究涉及的学科/课程、受教育阶段、出版类型等信息。(24)Mark W.Lipsey and David B.Wilson, Practical Meta-Analysis(Thousand Oaks：Sage Publication, 2001), 1-23.本研究的文献编码如下：

1.文献类型(Litrature type, Lt)：硕博论文编码为D，期刊论文编码为J。

2.样本量(Sample size, Ss)：参照艾伦(Alan)和罗伯特(Robert) 提出的标准(25)Alan C.K.Cheung and Robert E.Slavin,“Effects of Educational Technology Applications on Reading Outcomes for Struggling Readers: A Best Evidence Synthesis,”Reading Research Quarterly 48,no.3(2013)：277-299.，样本量大于250为大样本，编码为1，小于等于250为小样本，编码为2。

3.性别(Gender, Gen)：男性编码为1，女性编码为0，男女均有编码为2，未报告编码为缺失，编码表中以“-”代替。

4.受教育阶段(Grade, Gra)：样本学段处于小学阶段编码为E，中学阶段编码为M。

5.区域(Region, Re)：以文献中样本所在地区为准，具体包括美国(U.S.)、土耳其(TUR)、尼日利亚(NG)、阿拉伯联合酋长国(U.A.E.)、中国台湾和北京。

6.学科(Subject, Sub)：以纳入文献中学业成就所测试的学科为准，涉及科学、工程、数学、阅读和英语学科。

7.研究设计(Research design, Rd)：本研究中的研究设计涉及心理学中常用的研究类型：随机实验设计(Random-experimental design, Re)、准实验设计(Quasi-experimental design, Qe)、相关研究(Comparative design, Cd)和因果推断设计(Causal-comparative design, Ccd)。

8.STEM教育方法(STEM education method, Sem)：根据美国工程教育学会第120届学术会议上戴维(David)等人的报告，目前STEM教育主要包括四种典型的教学方法，分别是：问题式学习(Problem-based learning)、 项目式学习(Project-based learning)、设计式学习(Design-based learning)和探究式学习(Inquiry-based learning)。(26)David R.Heil et al.,“Understanding Integrated STEM Education: Report on a National Study, ”ASEE Annual Conference & Exposition, Atlanta, Georgia. 2013: 1-15．通过分析四种教学方法的内涵，将本研究中的具体教育方法分别归入对应的类别：问题式学习的前提假设是学习是一种能动的、整合的，受社会文化因素影响的建构过程。学生用先验知识解决真实情境中的复杂问题，同时获得新知识。其创造力和在现实世界中的问题解决能力在此过程中得到发展。包含原始文献中的STEM program、STEM school、STEM approach和Problem-based Learning。项目式学习强调教师在设计项目时，全面衡量教学内容的学科覆盖程度。不能局限于科学和数学两个学科，而工程和技术学科被认为是实现学科整合的基础和桥梁。STEM项目的合理性和有效性以跨学科性和整合性双重标准评定。原始文献中的STEM roles activity 、STEM lesson plan、STEM training、STEM method、ISTEMA method、Project-based Learning、integrated STEM、STEM education和STEM integration符合项目式学习的核心内涵。设计式学习是指教师从一个现实需求出发，引导学生进行概念设计、原型设计和测试的开发，最终创造一个能满足现实需求的产品。包含原始文献中的Engineering design-based、Engineering course和Computer-based probeware。探究式学习是一种研究性教学方法。学生通过提出问题，围绕这一问题设计和进行实验，再在实验数据分析基础上得出结论。在不断地总结和修正发现的过程中逐渐形成对知识的正确理解。包含原始文献中的Inquiry-based Science Instruction和Inquiry-based Learning。经整理，得到如表1所示的原始文献信息编码表：

(五)编码准确性评估

编码准确性对于元分析至关重要。本研究在进行元分析前，由两名研究者分别独立对文献进行编码，计算编码的一致性程度。根据一致性系数(Cohen kappa)大于0.7的统计要求(27)Ali Yldrm and Hasan Simsek, Sosyal Bilimlerde Nitel Arastirma Yontemleri [Qualitative Research Methods in Social Sciences](Ankara: Seckin Publication, 2011), 237-253.，本研究的编码一致性为0.9，证明本研究编码结果是可靠的。

四、研究结果

(一)效应量的计算与合并

计算与合并效应量是元分析的核心环节。西乌(Siu)认为，效应量不但能揭示预测变量作用的大小，而且可作为统一的度量标准用以比较包含相同变量的系列研究结果(28)Siu L.Chow,“Significance Test or Effect Size,”Psychological Bulletin 103, no.1(1988): 105-110.②Gulcan Sarican and Devrim Akgunduz,“The Impact of Integrated STEM Education on Academic Achievement, Reflective Thinking Skills towards Problem Solving and Permanence in Learning in Science Education,”Cypriot Journal of Educational Sciences 13, no.1(2018): 94-107.③Müzdelife Kurt and Semraanl Benzer,“An Investigation on the Effect of STEM Practices on Sixth Grade Students’ Academic Achievement, Problem Solving Skills, and Attitudes towards STEM,”Journal of Science Learning 3, no.2(2020): 79-88.④Dilber Acar et al.,“The Effects of STEM Training on the Academic Achievement of 4th Graders in Science and Mathematics and Their Views on STEM Training,”International Electronic Journal of Elementary Education 10,no.4(2018): 505-513.⑤John F.Moyer,“Probeware in 8th Grade Science: A Quasi-Experimental Study on Attitude and Achievement”(EdD diss., Wilmington University, 2013), 35-76.⑥Norma Olivarez,“The Impact of a STEM Program on Academic Achievement of Eighth Grade Students in a South Texas Middle School”(EdD diss., TEXAS A&M University Corpus Christi, 2012), 29-47.⑦Chemisi Asha Kogo-Masila,“A Comparative Study of Two Graduation Pathways: Traditional vs. STEM at a Southeastern High School”(EdD diss., Gardner Webb University, 2017), 38-86.⑧Cotabish Alicia et al.,“The Effects of a STEM Intervention on Elementary Students' Science Knowledge and Skills,”School Science and Mathematics 113, no.5(2013): 215-226.⑨Kyung Hee Kim et al.,“Project Clarion: Three Years of Science Instruction in Title I Schools among K-Third Grade Students,”Research in Science Education 42, no.5(2012): 813-829. Melanie Megias Eileen,“The Impact of High School Science, Technology, Engineering, and Mathematics (STEM) Magnet Programs on the Academic Performance of Students”(EdD Diss., The College of William and Mary, 2020), 47-98.Hind Gergi Abou Nasr Kassir,“The Effectiveness of the Science-Inquiry Teaching Approach on the Students’ Achievement and Engagement in the UAE Public Schools”(EdD Diss., The British University in Dubai, 2013), 22-47.Omotayo Ojaleye and Adeneye O.A.Awofala,“Blended Learning and Problem-Based Learning Instructional Strategies as Determinants of Senior Secondary School Students’ Achievement in Algebra，”International Journal of Research in Education and Science 4, no.2(2018): 486-501.。更为重要的是，人们可以通过元分析等技术手段，对效应量进行加权平均以获得研究的整体效应大小。

本研究通过提取42项研究的样本量、均值、标准差、统计量等信息，采用标准化平均差异(Standardized mean difference，SMD)公式计算单个研究效应量和合并效应量。教育研究中常用的SMD有Cohen’s d、Glass’s Δ、Hedges’s g等，在单次研究中计算SMD的常用指标是 Cohen’ d。(29)Jacob Cohen,Statistical Power Analysis for the Behavioral Sciences(New York: Lawrence Erlbaum Associates, 1988), 19-66.②Ann Robinson et al.,“The Effects of a Science-Focused STEM Intervention on Gifted Elementary Students’ Science Knowledge and Skills,”Journal of Advanced Academics 25, no.3(2014): 189-213.③Alfred Olufemi Fatade et al.,“Effect of Problem-Based Learning on Senior Secondary School Students Achievements in Further Mathematics,”Acta Didactica Napocensia 6, no.3(2013): 27-44. ④Abeera Parvaiz Rehmat,“Engineering the Path to Higher-Order Thinking in Elementary Education: a Problem-Based Learning Approach for STEM Integration”(PhD diss., University of Nevada, 2015), 69-110.⑤Deborah O.Maxwell et al.,“Effects of Using Inquiry-Based Learning on Science Achievement for Fifth-Grade Students,”Asia-Pacific Forum on Science Learning and Teaching 16, no.1(2015): 1-31.⑥Szu-Chun Fan and Kuang-Chao Yu,“How an Integrative STEM Curriculum can Benefit Students in Engineering Design Practices,”International Journal of Technology & Design Education 27,no.1(2015): 107-129. ⑦Akawo Angwal Yaki, “Enhancing Science Achievement Utilising an Integrated STEM Approach,”Malaysian Journal of Learning and Instruction 16, no.1(2019): 181-205.⑧Salih Gülen,“The Effect of STEM Roles on the Solution of Daily Life Problems,”Participatory Educational Research 6, no.2(2019): 37-50.⑨Salih Gülen and Süleyman Yaman,“The Effect of Integration of STEM Disciplines into Toulmin’s Argumentation Model on Students’Academic Achievement, Reflective Thinking, and Psychomotor Skills,” Journal of Turkish Science Education 16, no.2(2019): 216-230.David Proudfoot et al.,“STEM Certification in Georgia’s Schools: a Causal Comparative Study Using the Georgia Student Growth Model,”Georgia Educational Researcher 15,no.1(2018): 16-39.Meltem Alemdar,“The Impact of a Middle School Engineering Course on Students’ Academic Achievement and Non-Cognitive Skills,”International Journal of Education in Mathematics, Science and Technology 6, no.4(2018): 363-380.Hasan Özcan and Esra Koca,“The Impact of Teaching the Subject ‘Pressure’ with STEM Approach on the Academic Achievements of the Secondary School 7th Grade Students and Their Attitudes towards STEM,”Education and Science 44, no.198(2019): 201-227.Evelyn R.Tolliver,“The Effects of Science, Technology, Engineering and Mathematics (STEM) Education on Elementary Student Achievement in Urban Schools”(EdD diss.， Grand Canyon University, 2016), 70-111.Angela Anita Wade-Shepherd,“The Effect of Middle School STEM Curriculum on Science and Math Achievement Scores”(EdD diss., Union University, 2016), 54-98.Gülsüm Araz, “The Effect of Problem-Based Learning on the Elementary School Students’ Achievement in Genetics”(M.Ed diss., Middle East Technical University, 2007), 44-90. Susan E.Holveck, “Teaching for Conceptual Change in a Density Unit Taught to 7th Graders: Comparing Two Teaching Methodologies-Scientific Inquiry and a Traditional Approach” (EdD diss., University of Oregon, 2012), 64-218.Barth Katie Nicole, “An Investigation of the Effects of Integrating Science and Engineering Content and Pedagogy in an Elementary School Classroom”(MA diss., Brigham Young University, 2013), 25-45.但是，在计算整体效应时，采用这种方式计算小样本研究的SMD会导致效应量被高估。考虑到本研究中有不少研究是小样本，为降低计算偏差本研究采用Hedges’s g(以下简称g值)作为效应量估计指标。

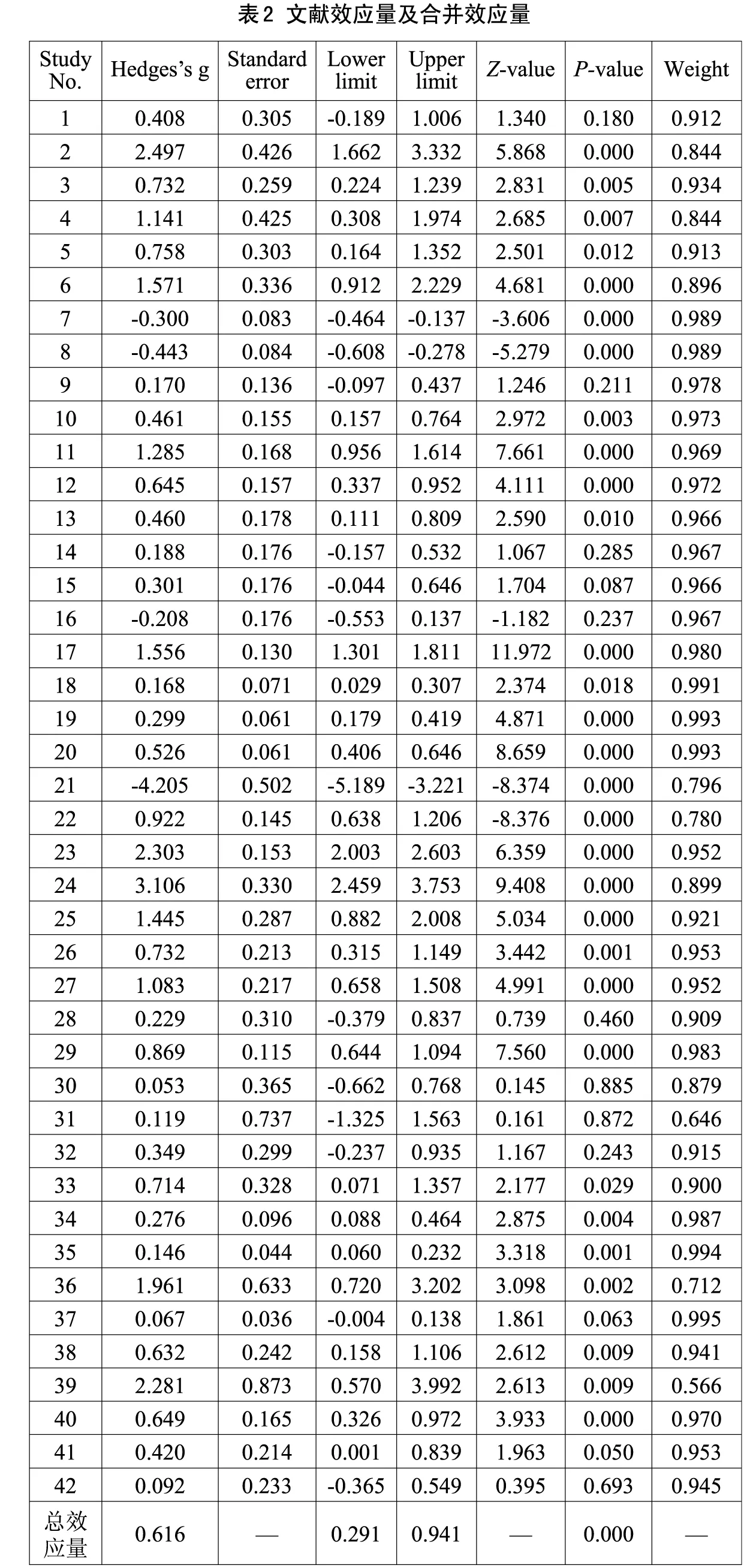
在估计合并效应量时，如果样本间存在异质性，需要采用随机效应模型进行分析，反之可采用固定效应模型。经检验，本研究存在异质性(Q=253.38，p<0.001)，故采用随机效应模型进行估计(30)Noel A.Card, Applied Meta-Analysis for Social Science Research(New York: Guilford Press, 2011), 107-257.。 效应量计算结果见表2：

根据雅各布(Jacob)的标准，0.2-0.49为小效应，0.50-0.79为中等效应，0.8及以上为大效应。由表2可知，从单个研究的效应量来看，报告大效应的研究有11篇，约占总研究的26%。报告中等程度效应量的研究有8篇，约占总研究的19%，其结果都显著。报告小效应的研究有9篇，约占总研究的21%，只有4篇具有统计意义。呈现负效应的研究有4篇，约占总研究的10%，其中有1篇研究结果不显著。效应量小于0.2的研究忽略不计。从所有研究的合并效应量来看，STEM教育组与传统教育组的标准化平均差异为0.616(p<0.001)，95%置信区间为[0.291, 0.941]，说明STEM教育对学业成就的影响显著。本研究的合并效应量属于中等效应范围。

(二)异质性分析

1.异质性检验

异质性检验(Heterogeneity test)，也叫效应量的齐性检验，是指对每个效应量的波动变化程度进行检验。如果各效应量之间的差异显著就表明研究之间存在真实差异，而非抽样误差。如果研究间是异质的，则需要进一步探究是否存在极端值(outliers)，即个别研究的效应量极大或极小，这些极端值都可能会影响总体效应量，甚至扭曲研究结果。评估异质性的常用指标有：Higgin’ s & Thompson’ s I2和Cochran’ s Q。本研究的异质性检验结果如下：

异质性检验结果表明，本研究纳入的研究之间具有强异质性(I2>80%，表示强异质性，且Q值显著)。在检出研究之间存在异质性后，需继续检测是否存在极端值。检测极端值的常用方法是观察某个研究效应量的置信区间与合并效应量的置信区间是否有重合，没有则认为该效应量是极端值。从表2可以得出7个极端值(研究2、8、11、17、21、23和24)，其中，研究8和21是极端小的效应，其置信区间的上限明显低于合并效应值置信区间的下限，研究11、17、21、23和24是极端大的效应，其置信区间的下限明显高于合并效应值置信区间的上限。

在剔除7个极端值后重新计算合并效应量，查看剔除前后研究结果的变化，以此判断极端值对综合效应量的影响。更新后的研究结果如表4所示：

由表4可知，剔除极端值后，合并效应量由0.616变为0.499，Q值也由817.33变为253.38。说明这7篇原始文献对总效应量的影响较大。

2.亚组分析与元回归

亚组分析(Subgroup analysis)，又称调节变量分析，是探索异质性来源的又一重要途径。元回归 (meta-regression)与亚组分析并没有本质区别，但两者在分析的数据类型上存在一定差异，元回归适用于调节变量是连续型数据的研究，亚组分析适用于调节变量是分类数据的研究。

调节变量的选取可以采用两种方式，一方面可以采用前人研究中揭示的STEM教育效果的影响因素，包括性别、家庭社会经济地位、种族、地域等。(31)Christopher S.Rozek et al.,“Reducing Socioeconomic Disparities in the STEM Pipeline through Student Emotion Regulation,”Proceedings of the National Academy of Sciences 116, no.5(2019): 1553-1558.另一方面可以参照以往元分析文献的经验，采用文献来源、样本量、研究设计类型、区域、学段和STEM教育方法等。(32)Nur Choiro Siregaret al., “The Effect of Science, Technology, Engineering and Mathematics (STEM) Program on Students’ Achievement in Mathematics: a Meta-Analysis,”International Electronic Journal of Mathematics Education 15, no.1(2019): 1-12.本研究综合考虑两种调节变量选取策略，采用样本量、学段、文献类型、学科、研究设计、教育方法和研究地区等变量为调节变量做亚组分析。分析结果如表5所示：

由表5可知，在样本量、学段、文献类型和研究设计中都没有发现明显的组间差异，表明这些变量并不调节综合效应的结果。而学科、STEM教育方法和研究地区组间差异显著，可以证明这些变量的不同亚组对综合效应的影响不同。就学科而言，科学和阅读都呈现中等程度的效应量(均大于0.5)，其他学科对学业成就的影响都是小效应量。就教育方法而言，项目式、问题式和探究式教学法的效应量较大。其中项目式教学法的效应量为0.722，接近高效应0.8。问题式和探究式教学法呈现中等效应。设计式教学法表现为较小的效应。就研究地区而言，土耳其、尼日利亚和中国台湾的效应量较大，分别为0.828、0.796和0.869。值得注意的是美国纳入研究量最多，但其效应量相对较小(g=0.318)。

元回归分析将研究发表年份作为预测变量，考察其对STEM教育与学业成就关系的影响，由表6可知，研究发表年份的调节效应并不显著，说明研究发表年份的不同，不会影响STEM教育与学业成就的关系。

(三)发表偏倚检验与效应量修正1.发表偏倚检验

发表偏倚也称出版偏差，是指在同类研究中，具有统计学意义的研究比不具有统计学意义的研究更容易被接收和发表，或者高效应量的研究比低效应量的研究更有可能被发表。(33)Michael Borenstein et al., Introduction to Meta-Analysis(New Jersey: John Wiley & Sons, 2009), 352-360.理想的元分析情境是能够得到所有符合纳入标准的研究，但这是不现实的，因为元分析研究者很难收集到相关领域的所有文献，比如没有公开发表的文章。在元分析中，直观地评定发表偏倚的方法是漏斗图，统计方法常用Egger检验。(34)Noel A.Card, Applied Meta-Analysis for Social Science Research(New York: Guilford Press, 2011), 107-257.如图2所示的漏斗图中，标准线左右分布的研究样本点明显不对称，说明存在一定的发表偏倚。继续采用定量的方法进行Egger检验，结果如表7所示，Egger检验的结果显著(t=3.669，p<0.01)。这也证明本研究存在发表偏倚。但研究者可以通过剪补法(trim and fill)(35)Sue Duval and Richard Tweedie,“Trim and Fill: a Simple Funnel-Plot-Based Method of Testing and Adjusting for Publication Bias in Meta-Analysis,”Biometrics 56, no.2(2000): 455-463.修正发表偏倚。

2.效应量修正

本研究运用剪补法，对效应量进行修正。该方法确定并修剪了13项研究。修剪后的总体效应量估计为 g = 0.216 (即SMD=0.216，p=0.045)。与原始结果g=0.499相比，修剪填充后的结果小于原始结果，这表明发表偏差使得效应量被高估，效应量放大了28.3%。将修剪后的结果保存下来，可以得到包含了推测的研究(即缺失的研究)在内的新的漏斗图。如图3所示，白色圆点为推测的缺失研究，灰色圆点为发表的研究。

以上分析结果表明，本研究修正后的效应量，已经在一定程度上消除了发表偏倚对分析结果的影响，研究结果较为稳健，即0.216更为接近STEM教育对中小学生学业成就影响的真实效应量。

五、结论与讨论

本研究运用元分析方法，探究了STEM教育对国内外中小学生学业成就的影响，并分析了影响STEM教育与学业成就关系的主要因素，得出如下两点结论。

(一)STEM教育有助于提升中小学生学业成就

研究结果表明，STEM教育比传统教育更有助于提升中小学生的学业成就，但提升程度较小(g=0.216)。通过分析发现，单个研究效应量和纳入文献的范围都对综合效应量有影响。

单个研究效应量直接影响综合效应量。本研究的综合效应量与许多相同主题的元分析一致(36)Nur Choiro Siregar et al.,“The Effect of Science, Technology, Engineering and Mathematics (STEM) Program on Students’ Achievement in Mathematics: a Meta-Analysis,”International Electronic Journal of Mathematics Education 15, no.1(2019): 1-12；Hakan Saraç, “The Effect of Science, Technology, Engineering and Mathematics-STEM Educational Practices on Students’ Learning Outcomes: a Meta-Analysis Study,”Turkish Online Journal of Educational Technology-TOJET 17, no.2(2018): 125-142；曾昭炳，姚继军．寻找“最佳证据”：如何运用元分析进行文献综述——以STEM教育对学生成绩的影响研究为例[J]．华东师范大学学报(教育科学版)，2020，(6)：70-85.，这些研究的效应量分别是0.242、0.442和0.410，都是较小的效应量。本研究中，呈现大效应的研究占总研究量的26%，中等效应量有19%，报告小效应量、负效应和不具有统计学意义的研究占纳入文献的55%。可见，原始文献中呈现中等程度以下效应量的研究比例大于中等及以上效应量的比例。同时，在计算综合效应量过程中，一部分研究的负效应与正效应相互抵消，导致总效应量偏小。在赛瑞格(Siregar)的研究中，也体现出类似的特点。但整体而言，本研究结果仍具有统计意义。

纳入文献的范围对综合效应量有一定影响。首先，本研究纳入的文献，其研究区域覆盖了国内外。其次，本研究将采用实验研究、相关研究或因果推断设计的文献都囊括在内。同时，所纳入文献涵盖了所有目前最典型的STEM教育方法。最后，本研究考察了STEM教育对多门学科学业成就的影响。既有元分析几乎没有同时满足上述四种条件的研究。本研究认为在综合考虑不同类型研究的基础上得出的综合效应值相对客观，且更为接近STEM教育对学业成就的真实影响。

(二)学科、STEM教育方法和地区变量调节STEM教育与中小学生学业成就的关系

本研究发现，所评估的学科、实施的STEM教育方法和研究地区的不同，是造成STEM教育对学生学业成就影响差异的关键因素。

就研究所评估的学科而言，组间异质性结果显著，这与已有研究结果相反。有研究者认为STEM学科之间有很高的融通性(37)Ali Bicer et al.,“Integrated STEM Assessment Model,”Eurasia Journal of Mathematics, Science and Technology Education 13, no.7 (2017): 3959-3968.，不同学科下，STEM教育对学业成就产生的影响相似。但本研究的结果恰恰证明了目前的STEM教育实践中，有效整合STEM学科的案例并不普遍(38)David R.Heil et al.,“Understanding Integrated STEM Education: Report on a National Study,”ASEE Annual Conference & Exposition, Atlanta, Georgia. 2013: 1-15.，学科壁垒现象依然存在。然而，本研究所体现出的差异p=0.048，与临界值0.05极为接近，说明学科间并没有极大的差异。随着STEM教育实践的深化和完善，大力发展学科融合和协同教学，能够有效打破学科壁垒，为提升学业成就助力。

就STEM教育方法而言，项目式、问题式、探究式教学法的效应均显著，这与以往研究结果基本一致。(39)Becker Kurt Henry and Kyungsuk Park, “Integrative Approaches among Science, Technology, Engineering, and Mathematics (STEM) Subjects on Students’ Learning: a Meta-Analysis,”Journal of STEM Education 12,no.5,(2011)，23-37；Zhao-Bing Zeng et al., “A Meta-Analysis on the Effects of STEM Education on Students’ Abilities,”Science Insights Education Frontiers 1, no.1(2018): 3-16.表明世界各国在大力推行STEM教育过程中，开发出了许多行之有效的STEM教育方法。这些方法虽具有各自的特征，但都体现了STEM教育的核心要义：融合多学科，解决现实问题。因此对学生的学业成就都起到了促进作用。值得注意的是，设计式教学法的效应量较小。本研究中这类教学法包括探索式计算机环境教学法和工程式教学法。该方法的效应量较小一方面是由于本研究纳入采用此类方法的文献数量较少，另一方面反映出这类方法运用的学科知识较为单一，对学业成就的提升效果有限。因此，在STEM教育实践中应注重选择恰当的方法进行教学，达到教学效果最大化。

就研究地区而言，土耳其的效应量达到0.8的高效应水平，土耳其STEM教育对中小学生学业成就的影响较其他国家更加明显。但是，作为STEM教育发源地的美国，其STEM教育对中小学生学业成就的作用只达到了中等偏上水平。毋庸置疑，地区差异是各类研究中最常被探讨的问题。大到各个国家政府对STEM的重视和投入程度存在差异，小到各国学生和家长对STEM教育的态度和动机不同，都会对STEM教育与学业成就的关系产生影响。地区差异带来的影响提示我们，在提升STEM教育水平和效果时，要根据本国国情采取适当的对策，不可急于求成，照搬别国经验。