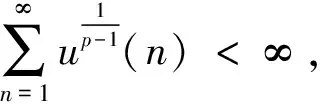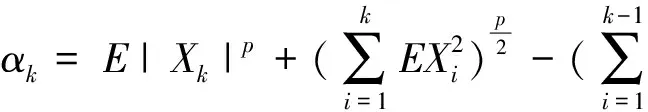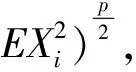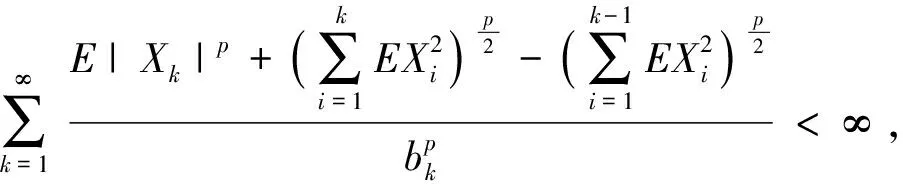AANA序列的Brunk-Prokhorov型强大数定律
冯德成,郑 蕊,谢静芳
(西北师范大学 数学与统计学院,兰州 730070)
1 预备知识
随机变量序列的极限理论是概率论研究的热点.其中具有优良性质的独立随机变量序列的极限理论研究已经十分成熟,但生活中绝大多数事物之间并非互不相关,而是有某种联系的.因此研究相依随机变量序列的极限理论具有更重要的现实意义.
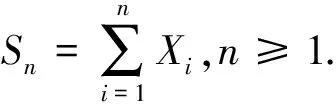
定义1设{Xn,n≥1}是一列随机变量序列,如果存在一列非负数u(n)且u(n)→0(n→∞),使得
Cov(f(Xn),g(Xn+1,Xn+2,…,Xn+k))≤u(n)
则称{Xn,n≥1}是AANA序列.这里n,k≥1且f,g是分量不减并且上述协方差存在的函数.
定义2如果对{1,2,…,k}的任意每对非空不相交子集合A1,A2满足
Cov(f1(Xi,i∈A1),f2(Xj,j∈A2))≤0[2],
则称随机变量X1,X2,…,Xk是NA的.其中f1,f2是使上式有意义的两个非降函数.进一步,称随机变量序列{Xn,n≥1}是NA序列,如果其任意有限子列是NA的.
相依随机变量序列种类很多,AANA序列是一种有广泛应用的相依序列.AANA序列的概念最早由Chandra等[3-4]给出,Chandra等得到了AANA序列的Kolmogorov型概率不等式、Marcinkiewicz-Zygmund型强大数定律及加权平均的几乎处处收敛性,之后国内外学者对AANA序列的研究更加深入.Ko等[5]得到了AANA序列的Hájek-Rényi型不等式;Wang等[6]推导出了AANA序列的乘积和的重对数律;Yuan等[7]又得到了AANA序列的Rosenthal型极大值不等式;Wang等[8]获得了AANA序列的强增长律与部分和序列上确界的可积性.
强大数定律是相依随机变量序列极限理论的重要课题,一直以来都是学者们关注的焦点问题.Brunk-Prokhorov强大数定律是强大数定律的一个重要组成.文献[9-12]得到了一些相依随机变量序列的Brunk-Prokhorov强大数定律.文献[13]研究了PA(相协)序列和NA序列的部分和序列在1 (1) (2) 引理3设{Xi,1≤i≤n}是均值为零的NA序列,p≥2.且对每一个1≤i≤n,有E|Xi|p<∞,则有 (3) 引理4设{Sn,n≥1}是一列随机变量序列,{bn,n≥1}是一列不减的无界正数序列,{αn,n≥1}是非负数序列.r和C是固定的正数.假定对每个n≥1有 则 并有增长率 这里 并且 (4) 此外如果假定对无限多个n,有αn>0,则 (5) 并有增长率 这里 并且 如果假定对无限多个n,有αn>0,则 这里,Dp与引理1中的Dp一致. 所以 取r=p,C=Dp,由引理4得 并有增长率 这里 由引理4中式(4)得 如果假定对无限多个n,有αn>0,由引理4中式(5)得 证毕. 下面证明当1 并有增长率 这里 并且 此外,如果假定对无限多个n,有αn>0,则 证明取αk=E|Xk|p,k为正整数,则αk≥0.由引理2中式(2)得 因此 由引理4,定理得证. 证毕. 由定义得NA序列是特殊的AANA序列,下面给出在p≥2时NA序列的Brunk-Prokhorov型强大数定律. 并有增长率 这里 并且 此外,如果假定对无限多个n,有αn>0,则 所以 再由引理4,定理得证. 证毕.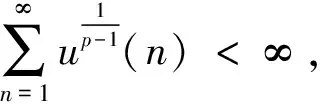
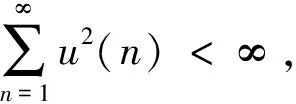
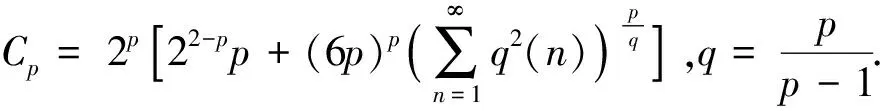
2 主要结论及证明