一种关于“判知结论浮动”现象的多元主义解释框架

徐英瑾

判知结论浮动（epistemic shift，直译为认知浮动）是西方知识论文献的一个常见说法。这个略显拗口的词组描述的是这样一种现象：一个认知主体持有的某信念，在某些条件下被知识裁判人（knowledge ascriber）判定为“知识”，而在另一些条件下被判定为“非知识”。举例来说：假设你是一位知识裁判人，现在请想象有个叫张三的人——他正看着自己一双充满老茧的手发呆。那么，你是否会裁定说“张三的确知道他有两只手”呢？笔者相信大多数人会给出肯定的回答。这样一来，“张三有两只手”就是张三的“知识”的一部分。然而，在另一语境中，张三尽管在盯着他的手发呆，你却被额外地告知：张三有可能就是一个“钵中之脑装置”的牺牲品（根据“钵中之脑”的思想实验，张三关于“自己有两只手”的幻觉是通过一位邪恶的科学家精心刺激他的大脑皮层所产生的。除了一个被放置在营养钵之中的大脑之外，张三就没有身体的其余部分）——在这种情况下，你是否会依然裁定说“张三的确知道他有两只手”呢？恐怕这时候你的裁定就不会那么斩钉截铁了。换言之，在引发“钵中之脑”之类的怀疑论思维的语境中，原本可以被判定为知识的信念，却无法被判断为知识。这就是所谓的“判知结论浮动”现象。

那么，我们究竟该如何解释这种判知结论浮动现象呢？不同的哲学家提供了不同的理论方案。例如，著名哲学家刘易斯（David Lewis）、亚利桑那大学的科恩（Stewart Cohen）、耶鲁大学的德罗斯（Keith DeRose）等语境主义者（contextualist）［1］（P91-123）［2］（P913-929）［3］［4］（P549-567），以及像罗格斯大学的夏佛（Jonathan Schaffer）这样的比对主义者（contrastivist）［5］（P73-103）均认为，判知结论浮动现象之所以发生，是因为知识裁定活动本身是敏感于那些可以为知识裁判人获知的语境信息的。也就是说，只要人们对“知道”的语义理解跟着语境变了，判知结论浮动现象也会随着发生。至于像斯坦利（Jason Stanley）［6］这样的“基于利害的不变主义者”（stake-based invariantists），则不是这样看问题的。他们在解释这一现象的时候，会诉诸那些与认知主体相关的因素，比如认知活动牵涉的旨趣与实践方面的利害关系。对于同类现象做出不同解释的还有“智性不变主义者”（intellectual invariantists），代表人物有多伦多大学的内格尔（Jennifer Nagel）。她主张运用与认知场景中的主体（而不是故事外的知识裁判人）自身相干的心理要素来解释判知结论浮动现象，而她采用的具体解释资源则来自心理学概念“固知需求（need-for-clo‐sure）”［7］。

不过，与某些读者的预期可能相反，笔者不会在上述立场中选边站，不会简单地提出一种新立场来反驳上面的任何一种理论。毋宁说，本文将构造一种大一统框架，以便在重构上述各种理论的基础上吸收其精华。而且笔者将说明，如果吾辈要以一种先天的方式来研究判知结论浮动问题的话，为何上述这种大一统框架乃是吾辈所能期盼之最佳结果。换言之，从元哲学的角度看，对于判知结论浮动的恰当哲学说明，必须容忍关于判知结果之沉浮的多种解释的多元性，以显示其应有的“海乃百川”的特征。而任何一种想在这些多元因素中凸出一点而不顾其余的做法，均会使得自己落入盲人摸象之境地。

一、导论：从“概率”含义的澄清说起

本文将利用特定的概率论规则（贝叶斯定理）构建大一统框架，理由在于：贝叶斯定理等概率规则都表达了特定的先天真理，对于它们的调用不太会遭遇明显的争议。所以，这些概率规则也就非常适合打造一个中立的理论框架，以供品鉴各种不同的知识论理论。

笔者注意到，此前已经有澳大利亚天主教大学的霍桑（John Hawthorne）和希伯来大学的克瓦特（Igal Kvart）两位学者做出了类似的尝试。他们在构建知识论框架时也将“知道”这一概念与概率论相联系（顺便说一句，英文中knowing与knowledge分享共同的词根，对于“知道”条件的讨论，基本等同于对于“知识”条件的讨论）。那么，笔者的框架与他们的工作又有哪些区别呢？

第一，笔者与那两位学者关于“概率”的定义不同。在克瓦特的理论中，概率既不是主观概率，也不是相对的概率，而是所谓的“客观的机遇”。他认为“概率”所刻画的，是在给定世界先验历史（a priorhis‐tory of the world）的情况下，出现某个经验事实发生之机遇［8］（P6）。而且，“世界的先验历史”是完全外在于知识裁判人的，是纯客观的。与之类似，霍桑也采用了客观主义版本的“概率”概念［9］（P28）。但是，在笔者看来，在知识论研究中运用这种客观主义色彩浓郁的“概率”观，不太妥当。正如罗格斯大学的古德曼（Alvin Goldman）所指出的，解释“知道”的含义基本相当于解释大多数人关于“知道”的语言直觉［10］（P199）。这在很大程度上属于心理学的范畴，与客观世界所具有的先天历史无太直接的联系。古德曼的描述中已经出现了一种打通心理学研究和知识论研究的倾向，这一倾向亦在内格尔的工作中被大大强化［7］。她直接采用心理学概念“固知需求”作为具体解释资源——顺便说一句，在心理学领域，该概念的提出者乃是克鲁格斯基（Arie Kruglanski）与韦伯斯特（Donna Webster）［11］。秉承古德曼、内格尔两人的精神，笔者使用的“概率”概念也是主观主义的。

第二，笔者与克瓦特、霍桑两位学者关于“概率”概念的适用范围不同。克瓦特的理论主要处理知觉知识［8］（P3）。笔者的理论不仅可以解释那些牵涉知觉知识的场景，还可以容纳诸多别的场景。

第三，笔者与克瓦特、霍桑两位学者各自的理论立场所具有的“宽容度指数”不同。为了解释日常生活中的知识评判现象，霍桑在其知识论构建中引入了所谓的“摩尔式的知识限制条件”［9］（P111），众所周知，G·E·摩尔乃是一位以尊重日常生活中的常识判断为著称的哲学家。但是，既然霍桑引入了摩尔式的知识限制条件，也就引入了一种接近于摩尔主义的常识主义立场，这种立场不可能兼容其他关于判知结论浮动的理论立场。与之相比，笔者的理论对所有立场保持中立，以超然的态度来评判各种不同的理论。

笔者无意给出一个完整的关于“知识”的定义，仅仅试图给出一种如何解释判知结论浮动现象的理论。有限的理论目的，将能够使笔者仅仅关注“知识”构成的必要条件，减少理论构建的负荷。

二、用概率论刻画“知”之底线

毫无疑问，要罗列“知识”得以成为知识的充分必要条件，是非常麻烦的。在知识论的研究史上，已经有太多人做出过努力，目下依然没有哪一项关于“知识”的定义得到学界的普遍赞同。既然本文的目的是去说明判知结论浮动现象，笔者就可以由此合理规避全面定义“知识”的任务，而只需要聚焦知识构成的某个必要条件，并把它设定为“知”之底线，一个信念至少应当先满足该底线所提出的要求，才有可能成为知识。这种研究思路来自木桶效应——木桶的水位取决于围成木桶诸木板的最低那块的高度，我们可以通过讨论那块最关键的（它往往就是最低的）木板的高度来讨论木桶的水位。同理，我们也可以通过对于某条“知”的底线高低的讨论，来介入判知结论浮动现象的讨论。

我们先对底线作粗线条勾勒。从一常识开始我们的探索：只有当一个主体所持有的信念是一个内容为真的信念时，我们才能说该信念是知识，或者说主体知道它。

例如，当一个小姑娘对你说，她知道“巴黎是英国的首都”，你一定不会觉得她真“知道”这一点，事实上伦敦才是英国的首都，“巴黎是英国的首都”是不符合事实的。说得抽象一点，要去判定某认知主体S是否“知道”某事P，至少需要检查两个条件是否满足：其一，S本人是否相信P；其二，该信念P是否与外部事实P相符。如果S的信念和外部事实不相符，P就不是知识，任何一个知识裁判人也就不能说S知道P。在此，“外部事实P”就可以被称为“P 的使真者（truth-maker，指对于使得内部信念为真的外部事实，下同）”。

现在我们就用“P内”指涉命题P在主体S心灵内部的信念表征，“P外”则指与P相关的外部事件。根据这样的记号，我们得出一个“知之底线”的刻画草案：

一个信念P被判断为“知识”，至少得满足条件：Pr（P外|P内）=1。

自然语言的翻译就是：一个信念P被判断为“知识”，至少得满足的条件：在P内本身已经被认为是真的前提下，我们计算P外的后验概率得到的结果是1。需要注意的是，讨论P内约束下的P外的后验概率，就等于讨论“针对P内这一现象的基于P外的解释的合理性”。举例来说，针对张三拥有“伦敦在英国”的信念这一有待解释的现象，我们搬出“伦敦的确就在英国”这一事实，是不是就能够完美地完成解释任务呢？如果草案里的概率值的确是取1的话，那么，问题的答案就是肯定的。

显然，这个公式用概率学的语言，刻画了前面提到的那条常识：只有当一个主体所持有的信念其内容为真时，才能说该信念是“知识”。

但我们还不能满足于这种刻画。按照上述刻画方案，知识裁判人将会永远将该主体的信念判定为知识，这样也就不会出现判知结论浮动现象。为了解释判知结论浮动现象，我们必须引入一个可以被度量的变量，而且这个变量恰好能够影响知识判定的结论。基于上述考量，笔者引出“知之底线”的刻画草案（改1）：

一个信念P被判断为“知识”，至少得满足条件：Pr（P外|P内）的值必须足够高。

“足够高”的确是一个含混的表达，但笔者是有意利用它的含混性，以包容不同的关于判知结论浮动的理论。

然而，这样的刻画还不能应对一些特殊的知识论案例，如下面的案例：有个名叫汉娜的小姑娘，还没上过学，对现代化学一无所知。可是，当有人问她各种化学问题的时候，她回答的竟然都对，这是因为有一个万事通小天使偷偷告诉她各种化学问题的答案了。假如信念P表示“一个甲烷分子是由一个碳原子和四个氢原子组成的”，显然P在外部世界中是真的，即P外的值为1。在小天使的耳语下，汉娜又的确产生了信念P，而且相信P是真的，故此，P内的值为1。这样一来，表达式Pr（P外|P内）的值应该也是1。根据前文的定义，作为知识裁判人的我们此刻应当判定汉娜知道关于甲烷的化学构成的知识。但是在直观上，恐怕很多人未必会觉得汉娜知道这一点。不少人会倾向于说：真正知道化学知识的是小天使，而不是汉娜，后者只是鹦鹉学舌罢了。

即使面对上述反例，从纯粹逻辑角度看，我们似乎还是能够坚持关于“知之底线”的刻画草案，因为该草案仅仅涉及“知道”的必要条件，而非充分必要条件。然而，仅仅从这个角度应对反驳，又会使得草案显得过于粗糙而缺乏对于“知识”之本质的穿透力。因此，我们最好还是沿着上述反例提出的思路，细化草案。由此，读者给出了修改方案“知之底线”的刻画草案（改2）：

一个信念P被判断为“知识”，至少得满足条件：我们（知识裁定人）在评估Pr（P外|P内）值的时候，考虑到P（rX）的抵消作用，发现这个值依然必须足够高。

那么，这里出现的X是指什么呢？笔者把X称为“异常使真者”（Abnormal Truth-maker），也就是使得内部信念成真的外部因素中的异常者。这是相对于“常规使真者”（Normal Truth-maker）而言的。在汉娜接受化学测试的例子中，“一个甲烷分子在事实上的确是由一个碳原子和四个氢原子组成的”这一点，就是一个“常规使真者”。但汉娜没接受过科学教育，这个使真者自身无法独立地解释她为何会具有甲烷构成的真信念。所以，我们就得引入一个“异常使真者”来解释，此即那个天使的作用。“异常使真者”的出现，会使得知识裁判人更不倾向于认为汉娜是具有知识的，因此，我们就必须在考察Pr（P外|P内）值的时候，充分考虑Pr（X）的值——它其实就是“异常使真者”出现的先验概率值——的大小，并将其作为干扰因素予以扣除。我们可以得到“知之底线”的刻画草案（改3）：

一个信念P被判断为“知识”，至少得满足的条件：Pr（P外|P内）的值足够高，且Pr（P外|P内）= 1- Pr（X）。

对于“Pr（P外|P内）= 1- Pr（X）”这一结论的概率推算如下：

先根据贝叶斯定理计算Pr（P外|P内）：

（1）Pr（P外|P内）= Pr（P内|P外）× Pr（P外）/Pr（P内）

要算出等式左边的值，我们显然要计算等式右边诸项的值。P内的概率值必须是1（因为根据某种“准笛卡尔主义”的理论精神，内在信念的可靠性基本是不可怀疑的）。但是如何确定Pr（P内|P外）的值呢？笔者认为此值也是1。这是基于一种常识性的考虑，即与P相关的事实在通常情况下会产生与P相关的真实信念。

由（1）可得（2）：

（2）Pr（P外|P内）= 1 × Pr（P外）/1= Pr（P外）

那么，我们又该如何确定Pr（P外）值？笔者建议采用“全概率公式（Law of total probability）”，据此，得到：

（3）Pr（P内）=1= Pr（P内|P外）× Pr（P外）+ Pr（P内|X）×Pr（X）

=1 × Pr（P外）+1 × Pr（X）

=Pr（P外）+ Pr（X）

据此，

（4）Pr（P外）=1-Pr（X）

结合（2）与（4），得到：

（5）Pr（P外|P内）= 1-Pr（X）

当然，可以降低Pr（P外|P内）值的“异常使真者”的数目可能不止一个。考虑到这一点，上述草案应被升级为“知之底线”的刻画草案（改4）：

一个信念P被判断为“知识”，至少得满足的条件：Pr（P外|P内）的值足够高，且Pr（P外|P内）(Xi)（n≤N）。

对于上述公式的自然语言表达：在关于P的内部表征已经被确定的情况下，该内部表征的知识地位的稳固度，等于1减去所有使得P内得以产生的“异常使真者”的概率之和后的余数。此处，N指知识裁判人所能想到的异常使真者的最大数目。如何确定N的值，与对于知识裁判人本人的工作记忆容量的评判结果相关。

根据“草案（改4）”可知，诸“异常使真者”对知识的颠覆力越大，知识裁判人就越不会倾向于把信念判定为知识，反之亦然。所以，对于判知结论浮动现象的讨论就能被转化为这样一个问题：知识裁判人能想到多少个异常使真者，以及每一个异常使真者在知识裁判人眼中的知识颠覆力有多大。这些颠覆力的加权和，就是(Xi)的值。

语境主义者、比对主义者、基于利害的不变主义者和智性不变主义者都可能对笔者的这种貌似过于缺乏断言内容的建议提出异议。他们可能不反对笔者对“异常使真者”的刻画方式，但会进一步提出：我们应该聚焦于某个更重要的认知因素，以便更为细致地刻画“异常使真者”对于知识的颠覆力。在语境主义者眼中，这个更重要的因素是“语境因素”［2］（P913-929）［3］（P1-52）；在比对主义者眼里，该因素便是“语境比对项（Semantic Contrast）”［5］，而在“基于利害的不变论者”眼中，该因素便是“利害关系”（Stakes）［6］，而在“智性不变论者”那里，该因素是“固知需求”（Need-for-Closure）［7］。

在笔者看来，所有这些理论都犯了以偏概全的错误。下面笔者先来批评语境主义。

三、透过“合理性”与“敏感性”概念重构语境主义

在一般的谈话中，没人会觉得自己是“钵中之脑”，而在哲学教师教授怀疑论的哲学课堂中，我们却很有可能会怀疑自己的确就是“钵中之脑”。在语境主义者看来，之所以我们会对于“自己是不是钵中之脑”问题产生不同的答案，要害就在于：知识判定的语义标准会依语境而变化——在日常谈话的语境中，这个标准是比较低的，而在引发怀疑论思维的语境中，该标准会被提高。那么，为何日常谈话的语境与引发怀疑论的语境能够各自提出不同的知识标准呢？对于该问题，不同的语境主义者的解答方案是彼此不一样的。比如，根据亚利桑那大学的科恩教授的观点，这主要取决于一个相关的“异常使真者”所具有的合理性程度究竟有多高［1］；而耶鲁大学的德罗斯教授认为这牵涉到我们的目标信念自身所具有的敏感性的程度都有多大［3］。

先讨论科恩的想法，那是基于合理性的语境主义：

当且仅当如下的条件被满足时，对于目标信念P而言，对于该信念的一个异常使真者h必须要被知识裁判人所考虑到：即在特定理由r被给定的情况下，h自身所具有的后验概率必须足够高。其中，“足够高”的标准则取决于特定的语境的规定［1］。

举例而言：假设目标信念P是“我看到了一个看上去是斑马的动物”。对信念P来说，有两个竞争解释：一个解释表征了“正常的使真者”，即我眼前真有一匹斑马。另一个解释由“异常使真者”提供：我所看到的并非是斑马，而是被精心涂抹成斑马的骡子。那么，对于知识裁判人来说，“我所看到的只是一头被涂成斑马花色的骡子”这个假设，是否应该被考虑呢？这取决于在给定动物园的环境和知识裁判人已知的信息的情况下，该假设自身成真的后验概率有多高。如果它的后验概率高过了一定的阈值，这个解释就是相关的，应当被纳入考虑范围。阈值有多高，由语境本身来决定。

科恩的描述已经颇具概率论色彩，可以被轻易顺化为笔者的解释框架。略为麻烦的是对基于“敏感性”概念的语境主义的概率化重述。

什么叫“敏感性”？这个概念是美国哲学家诺齐克（Robert Nozick）提出的。根据他的看法，若一个主体S是以具有“敏感性”的方式去持有信念P的，那么这就能保证S是的确知道P的。“敏感性”条件之被满足，当且仅当如下条件被满足：只有在P自身是真的情况下，P才能够被S所相信——反之，如果信念P本身非真，那么主体S就不会相信P［12］。譬如，如果法国的首都的确不是柏林，那么，张三就不会相信法国的首都是柏林；如果张三的确不是钵中之脑，则张三就不会相信自己是钵中之脑。从这个意义上说，S的信念是敏感于P自身的真值的，并与其有“随动关系”（P的成立对应于S关于P的正向信念，而P的不成立则对应于S关于P的否定性信念）。德罗斯在表述他自己的语境主义概念时，利用了诺奇克的“敏感性”概念，这是基于敏感性的语境主义：

当我们要确定某个主体S知道或不知道某个命题P时，在某些必要的情况下（特指怀疑论语境出现的情况——引者注），知识的标准就会提高到这样的水平：主体S对于命题P的拥有方式必须具有敏感性，以便使得这个信念P本身能够被视为知识的一部分［3］（P36）。

乍一看，德罗斯的上述说法没有涉及概率学的术语，很难被顺化为笔者的表述框架。这里的一个明显技术麻烦是：传统上用来描述敏感性的技术框架乃是“可能世界语义学”，而非概率论。但笔者依然认为这种顺化乃是可能的。很明显，用概率论的方式来直接表征敏感性，我们就必须诉诸Pr（~P内|~P外）的值（该公式的意思是：相应外部事实P自身不存在的情况下，相应的内部表征也不存在的后验概率）。这个值应当比较高（非常接近1），以便表示这样的一个想法：相应外部事实P自身不存在的情况下，相应内部表征也不存在的可能性也非常高。这便构成了对于“敏感性”的下述含义的改写：

当P自身非真时，S就基本上会去相信“非P”。

那么，如何进一步确定“Pr（~P内|~P外）”自身的值非常高的条件呢？我们不妨先利用贝叶斯定理来计算Pr（~P内|~P外），可得：

（6）Pr（~P内|~P外）=Pr（~P外|~P内）×Pr（~P内）/Pr（~P外）

为了计算等式右边的值，我们需要先确定Pr（~P内）和Pr（~P外）的值。两者均包含了否定性表征，或者说，均涉及了对于否定性事件的概率的赋值。那么，此类事件的概率究竟该如何赋值呢？笔者认为这不是一个容易解决的问题。正像蒯因（W.V.Quine）指出的，以否定性的方式得到表征的表达式——比如“非乌鸦”——是无法直接对应于世界中的自然类的，而是人为约定的产物［13］。换句话说，人们可以随机确定某物为“非乌鸦”，比如桌子、电脑、布谷鸟，等等，而这些事物之间并无正面的共享特征将其连接到一起。这种做法显然将导致指称的含混性。要清除这种含混性，我们就必须对此类否定性表征所留下的逻辑空间包含的事物进行更加细致的区分。举例而言，我们若想要计算“不下雨”的概率，实际上我们就得计算“天晴”“多云”“下雪”等所有能够被归类为“不下雨”事件的概率的析取值。为了计算一个否定性事件的概率，我们就不得不计算一系列能够被囊括为该否定性事件的所有的正面的子事件的概率。这也是我们在以概率论的术语刻画“敏感性”时不得不采用的策略。

在进行了此番的操作后，“非P”之类的表达，就必须被兑现为一个个以正面方式得到表征的子事件。这些子事件的数量是海量的——譬如，对应“并非我眼前有一匹斑马”这个否定性的表达，就会有无数个以正面形式出现的命题：“我眼前有一头骆驼”“我眼前有一个外星人”，等等。但并非所有的命题都与怀疑论的哲学困惑有关，因为怀疑论的肯綮在于：任何一个既具有“非P外”的血统，又不具备“非P外”之外观的、并以正面形式被表述出来的命题，恰好能够用来解释“P内”在认知主体表征系统内部的生成。也正因为这一点，认知主体才会在该解释与基于“P外”的“正常解释”之间反复踟蹰，怀疑再三。这一点当然就会导致“Pr（P内|~P外）”的值与“Pr（P内|P外）”的值彼此大约相等（大约都是50%），让人无法找出优胜者。这也会导致整个“Pr（~P内|~P外）”的值——这也就是对于“敏感度”的度量值——的降低。从概率学的角度看，如果“Pr（P内|~P外）”的值接近50%的话，“Pr（~P内|~P外）”的值是不可能接近1的（好比说，如果你知道不下雨会将人渴死的概率只有50%的话，你是无法从中推出同等条件下人不渴死的概率是接近1的。后者的值应当也接近50%才对）。这也就是说，怀疑论的语境，就是那些使得“Pr（~P内|~P外）”的值得以被明显降低的语境。

在这些怀疑论语境中出现的任何一个既具有“非P外”的血统，又不具备“非P外”之外观的、并以正面形式被表述出来的命题，既然都能用来解释“P内”在认知主体表征系统内部的生成，它们就是使得“P内”为真的“异常使真者”，它们的“知识颠覆力”——在此就是指“敏感性颠覆力”的大小——可以通过对于的值的估量而得到判定。由此，语境主义的话语框架，也就被顺化为笔者的话语框架。

四、“异常使真者”如何在语境主义的框架中被甄别

在上节中，笔者仅仅是在形式上把科恩和德罗斯的语境主义叙述方式顺化为笔者的叙述方式，但不意味着语境主义本身是一种站得住脚的立场。笔者对语境主义的疑虑在于：他们是否提出了一些相应的规则，以说明为何某些“异常使真者”需要我们在考虑怀疑论的问题时被加以考量，而有些则不需要被加以考量？就笔者所知的范围内，在该问题上给出最系统思考的语境主义者乃是大卫·刘易斯（David Lewis）。他提出了一系列规则，用以甄别出哪些“异常使真者”是不能被忽略的［4］。笔者在此仅仅提到二者，一是保守主义规则：

那些从常识角度看，不能被忽略的“异常使真者”是不能被忽略的。

譬如，如果你生活在一个假斑马充斥的世界中的话，那么“假斑马很多”就会成为你的常识的一部分。这样一来，“你看到的所谓斑马就是被精心涂抹的骡子”的那种可能性就不能被忽略［4］（P559）。不过这也就意味着：那些从常识角度看可以被忽略的“异常使真者”，大约是可以被忽略的。

二是注意力规则：

那些在特定的谈话语境中，的确引发谈话人之注意的“异常使真者”乃是不能被忽略的［4］（P559）。

举例来说，在哲学教师教授怀疑论思想的课堂上，“钵中之脑”的假设如果的确引发了同学们的兴趣与注意的话，那么，在解释“为何我看上去有两只手”这一点时，同学们就无法忽略“这一信念是由一台复杂的钵中之脑装置所引发”这一异常的解释。

笔者的担忧是：这两条规则似乎互相打架。“注意力规则”实际上具有求新、求异的意蕴，故此新闻界才有谚语说“狗咬人不是新闻，人咬狗才是新闻”。但“保守主义规则”则具有反向的意蕴，该规则不鼓励大家天马行空地胡思乱想。譬如，除非“钵中之脑”的案例的确已经大量出现在了生活之中，并成了我们常识的一部分，否则，在知识论讨论中引入基于该案例的“异常使真者”，就是白费力气。

从论证的责任来看，究竟该如何顺化上述这些规则的关系，乃是语境主义者自己的事情。但在他们澄清这一问题之前，我们不妨就可以认为语境主义在不少重要细节方面具有瑕疵。与之相比较，笔者对于“判知结论浮动”的一般性解释框架就不用承担这种解释负担。道理是非常简单的：笔者的解释框架只是用来展示各种关于“判知结论浮动”的特定理论的一种中立性平台，缺乏细节不是对该平台的合适指控。

下面我们重述并评估别的关于判知结论浮动的特定知识论理论，以“基于利害的不变主义”为例。

五、重估“基于利害的不变主义”

“基于利害的不变主义”或“与利害相关的不变论（Interest-Relative Invariantism）”是指这样一种立场：相关的认知主体是否会将一个目标信念视为知识，在相当程度上与此类赋知活动带给他的实际好处或者坏处有关。具体而言，当相关主体的现实利益处于高风险时，其做出错误判断所要带来的代价也较大，这样一来，我们就更难说该主体所持有的相关信念P乃是知识的一部分，反之亦然。

若用笔者的模型来表达，上述立场就相当于以下两种说法的结合：

（甲）“草案（改4）”是成立的，即：Pr（P外|P内）=

（乙）对于任何一个解释“P内”的备选性解释而言，当且仅当有足够的利害关系与之牵扯时，它才值得被填入“Xi”槽中。在此“Xi”是指那些有特定的利害或兴趣与之相关的“异常使真者”。

本节所谈的这种立场的意蕴，可以通过“银行案例”来加以说明。假如张三背着巨额房贷，而且，张三还相信每月最后一个周日是当月还贷的最后期限。现在再假设有两种可能引发了他的这个信念：其一，该信念是基于他对于银行还贷日的正确的记忆；第二，该信念是基于他对于银行还贷日的错误的记忆。假设张三的财务情况非常好，那么即使他搞错了还贷的日子，他的信用记录也不会因此而留下污点。这样一来，“错误记忆”这一“异常使真者”所导致的知识削弱力就不会太大，并因此可以被忽略。反之，如果张三的财务情况是入不敷出的，那么，及时还贷就会对其征信记录的清白产生莫大的影响。在这种情况下，“错误记忆”这一“异常使真者”所导致的知识削弱力就会被放大，并因此无法被忽略。这也就是说，在张三本身的财务风险不大时，“草案（改4）”中“”的值会变得很小，“” 的值就会随之较大，而“Pr（P外|P内）”的值也相应会变得较大。这样一来，张三的相关信念就更容易被判定为知识的一部分。但是，如果张三的信用风险很高，那么，“草案（改4）”中的值就会随之变大，的值就会随之变小，而“Pr（P外|P内）”的值也会随之下降。这样，张三的相关信念就更难被判为知识的一部分。

由此看来，“基于利害的不变主义”是可以被顺化为笔者的模型的某种变体的。

但这种学说本身却依然是有问题的。正如罗格斯大学的夏佛（Jonathan Schaffer）所指出的，“基于利害的不变主义”无法处理类似钵中之脑等怀疑论案例［14］（P87-107）。举个例子：在张三看着自己的两只手的时候，他是否知道自己有两只手呢？在这个问题中，“我有两只手”这个信念被“钵中之脑之类的装置所引发”这种可能性是否应该被忽略呢？在哲学课堂上，这种可能性大概率是不应被忽略的。但这并不因为“钵中之脑”这种设想与张三有任何利害关系，而仅仅是因为我们在理论上不应忽略这种可能性。从这个角度看，“基于利害的不变主义”无法处理怀疑论等案例，因此，该立场不具备普遍可应用性。

上述的批评甚至还可以被施加到对于施罗德（Mark Schroeder）对于斯坦利的“基于利害的不变主义”的改进方案之上［15］。他的改进方案的核心思想是：

只要下述条件被满足，那么，S相信p的理由就至少与S相信~p的理由一样充足：

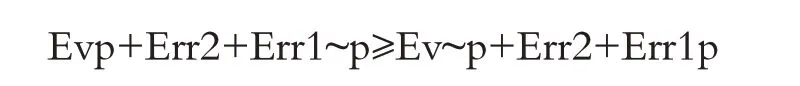
这个公式的意思是：S用以支持p的证据强度、S犯下“乙型错误”的代价以及S犯下“相信～p的甲型错误”的代价之和，必须大于或等于S用以支持～p的证据强度、S犯下“乙型错误”的代价以及S犯下“相信p的甲型错误”的代价之和（这里所说的“甲型错误”是指“将某个命题的真值搞反的错误”，“乙型错误”则是指“将某类事项完全忽略的错误”）。

对于施罗德的上述意见，笔者的反驳是：他是否提出了某种统一的量纲，以便我们去统一地计算“S用以支持p的证据强度”“S犯下乙型错误的代价”等变量的值呢？如果施罗德无法给出这种计量方法的话，那么，他的方案就无法具有真正的普遍适用性。

在下文，笔者将考察“不变主义”的另一个变体——“智性不变主义”。

六、重估“智性不变主义”

根据内格尔的“智性不变主义”观点，“判知结论浮动”现象不能通过主体所处的环境要素来解释，而应通过主体内部的信念形成过程来描述［7］。这就牵涉到“固知需求”这一心理变量。

心理学家克鲁格斯基和韦伯斯特将“固知需求”定义为：在一个特定的话题上，心理主体有特定的心理需求，而将某些信息固定为知识。固知需求这一心理学变量既能体现出个体差别（比如有人在固定知识的过程中显得性急，有人则显得拖沓），也能够体现出环境差异（比如同一个人在某些环境下会倾向于立即给出问题的答案，在有些环境下会举棋不定）［11］。

内格尔用固知需求重新解释了前文提到的银行案例，大意是：一个人的财务风险越高，其搞错银行还贷日带给他的潜在麻烦就越大，因此，他也就有更多的理由去反复检查还贷日期是否真被搞错了。在这样的情况下，他的固知需求就会变得比较小，而他做出有银行还贷日的知识指派的效率也会被降低。反之，一个人的财务风险越小，其搞错银行还贷日带给他的潜在麻烦就越小，因此，他也就缺乏更多的理由去反复检查还贷日期是否真被搞错了。在这样的情况下，他的固知需求就会变得比较大，而他做出有关于银行还贷日的知识指派的效率也会被提高［7］（P289）。

尽管内格尔描述的固知需求似乎只与利害关系相关，但实际上她提到了其他几个影响固知需求的因素，比如时间压力、疲劳程度、背景噪音，等等［7］（P288）。她没有提供一个统一的模型来解释这些因素是如何彼此融合、相互协调的，但至少她的确对判知结论浮动的动力因机制采取了一种多元主义观点。这与笔者的模型所隐含的多元主义思想颇为接近。内格尔的理论可以通过笔者的模型被重构如下：

（甲）“草案（改4）”是成立的，即：Pr（P外|P内）= 1

（乙）对于任何一个解释P内的“候选使真者”，当且仅当它附带一个比较低的“固知需求”的值时，它才值得被填入Xi槽中。

在笔者看来，内格尔的理论还是不够多元性，她忽略了一些在原则上无法被还原为固知需求的要素——这些要素对于解释判知结论浮动现象来说，的确是颇为重要的。笔者想到的这一被内格尔所忽略的要素，与知识裁判人自身的社会角色转变颇为相关。

为何要考虑这一要素呢？

古德曼就曾提出，在面对“钵中之脑”之类的玄想时，经过良好训练的哲学从业者会比普通人更快入戏。即使在面临一个日常生活中的信念时，哲学家或哲学系的学生也会比一般人考虑更多的“异常使真者”［10］。从这个角度看，作为一种社会现象，哲学教育的功能便体现于：它能够帮助从业者迅速从日常的思维频道切换到哲学的（特别是怀疑论）思维频道。

笔者认为古德曼的考量颇有道理。但他的这段评论却给内格尔的理论带来了麻烦，因为古德曼所谈到的关涉到社会角色转变的要素，是无法被顺化为固知需求的。为何这么说呢？

关键在于“时间”这一变量。众所周知，任何的心理过程的展开，包括知识判定活动，都需要花费时间。对于一个受良好训练的哲学从业者而言，在进行知识判定时，他只需要消耗非常少的时间，就可以从普通人的思维模式迅速切换到哲学从业者的思维模式，由此熟稔地处理“钵中之脑”的怀疑论案例。

另外，按照内格尔的理论，对于“钵中之脑”这类案例的研究却显然需要降低固知需求，以便为主体争取更多的时间来评估相关“异常使真者”的合理性。这样一来，面对同一案例，相关评判人的社会角色转换所需时间越短，其固知需求就会随之降低，导致判知时间延长。因此，社会角色的快速切换所导致的时间消耗量，与固知需求所导致的时间消耗量，在量的特征方面彼此相反。与社会角色切换相关的要素就很可能是固知需求之外的一个独立要素，不能被简单还原为后者（好比说，当你在检查一个宏观的经济运作体系的时候，如果有某种生产模式被发现一直在增加碳排放量，另外一种生产模式则一直在削减此类排放，那么，这两种模式就极可能是彼此独立，而不可被彼此还原）。但内格尔的模型没有提到这一独立要素，那么，她关于判知结果浮动效应的解释模型就是有所遗漏的。与之相比，笔者的理论模型没有对任何导致判知结果浮动效应的特定解释进行偏袒，也就不存在遗漏某项特定要素的问题。

七、结 论

语境、利害关系、固知需求等要素都对判知结论浮动现象有所影响，但它们都只强调了现象得以发生的某个特殊方面。语境主义者无法说明如何恰当地甄别那些值得关注的“异常使真者”；“基于利害的不变论者”则无法恰当地处理那些没有明显的利害牵扯的怀疑论案例；至于基于“固知需求”的智性不变主义者，则无法解释那些不可被还原为“固知需求”的社会因素在知识指派中的作用。针对笔者对于上述立场的批评，有人也可以反驳说：我们为何不能找到更多的影响判知结论浮动的要素，全面升级前面的理论呢？笔者对此建议的回复是：升级虽然在逻辑上可行，但被涉及的因素越多，模型就会包含越多的语言学、心理学或社会学成分，最终使得相关的理论模型具有更强的实证科学气味，而由此远离哲学。如果想停留在哲学层面上讨论相关问题，我们就只能满足于刻画判知结论浮动何以可能的诸要素的形式特征。这也是本文概括出来的“草案（改4）”完成了的工作。该模型既能提供一些关于判知结论升降的先天真理（并因此足够哲学化），又对所有现有的关于“判知结论浮动”现象的经验性解释保持中立（并因此足够海纳百川），实为哲学家所能期盼的关于此现象的最终解释了。