基于模糊数学的博弈论组合赋权法边坡稳定性评价
周锦涛
(三峡大学水利与环境学院,湖北 宜昌 443000)
边坡失稳是工程中常见的问题,严重影响着工程安全,而边坡稳定性评价在边坡工程有着重要的作用,是判断边坡是否失稳的重要依据,所以如何对边坡的稳定性进行合理评价是一个值得研究的问题。目前,很多专家提出了不同的意见,王采庆等[1]将天然边坡看作是部分信息已知、部分信息未知的灰色系统,用灰色聚类方法预测其稳定性;李克钢等[2]采用改进的动态权值评价方法,对边坡稳定性进行评价,利用关联度函数在一定程度上克服了专家评分的主观性;赵永虎等[3]利用可拓理论建立了物元模型,结合灰色关联分析法确定各评价因子的权重,对黄土斜坡进行稳定性评价,弥补了可拓法中权重难以确定的不足。上述研究成果在实际应用中取得了较好的效果,但存在一定局限性,对于边坡稳定性评价,最主要的问题就是确定合理的指标权重。灰色聚类法在聚类指标的选取过程中,过于依赖经验性质,精度较低;改进的动态权值评价方法虽然改善了确定权重过程中的主观性问题,但对于理想对象的选取尚无统一标准。
本文在上述研究基础上提出基于模糊数学的模糊综合评价模型,采用博弈论思想将以层次分析法确定的主观权重和以熵权法确定的客观权重组合起来得到组合权重,兼顾了主客观两方面,综合考虑指标之间的关系,赋权结果较2种单一的赋权方法更科学合理,从而为边坡的治理提供科学依据和建议。
1 模糊综合评价模型的建立
边坡的稳定性是由多种因素共同影响的结果,为了综合考虑多种因素的影响,本文结合蒋家淌滑坡实例建立了模糊综合评价模型[4-5],将边坡评价过程中难以量化的、非确定性指标的定性评价转化为定量评价,使每个评价指标相对于不同的等级都有不同的隶属度,评价结果更清晰。
1.1 评价指标的确定及评价等级的划分
根据边坡的实际地质环境条件和评价系统的合理性[6-7],选取地形地貌、地质结构、岩土性质、赋存环境4个一级指标Ci,以及坡高、节理发育与组合、内摩擦角、大气降雨等16个二级指标Cij,见图1。

图1 边坡稳定性综合评价指标
根据岩质边坡的稳定性,结合蒋家趟边坡地质情况将评价结果划分为4个等级[8],即:稳定(Ⅰ)、较稳定(Ⅱ)、不稳定(Ⅲ)、极不稳定(Ⅳ),表示为Nj={N1,N2,N3,N4}={Ⅰ,Ⅱ,Ⅲ,Ⅳ}。
1.2 确定模糊关系矩阵
分别对每一个因素进行评价,确定评价对象对评价集合Ni的隶属程度,从而得到模糊关系矩阵R。例如对一级指标C1,其模糊关系矩阵如下:
(1)
式中rij——一级指标C1中第i个二级指标对于评价等级j的隶属程度。
1.2.1定量指标
对所有指标进行考察得知,坡高、坡脚、植被覆盖率、内摩擦角、黏聚力、大气降雨为定量因素,故采用岭形分布函数确定其隶属度取值[9]。
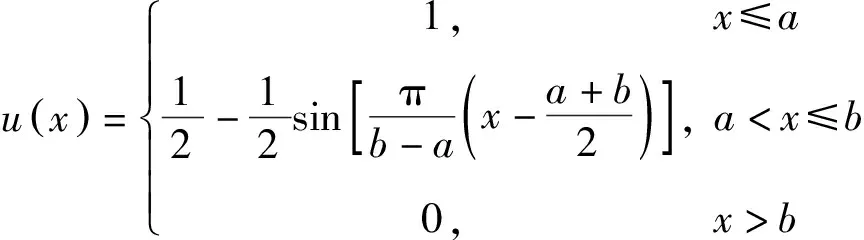
(2)
(3)
(4)
式中x——评价指标的实际取值;a、b、c——评价级别的基准界限值,对于输入的定量数据,经隶属函数模糊化后写成矢量式uⅠ(x)、uⅡ(x)、uⅢ(x)、uⅣ(x),它们分别对应定量指标各评语的隶属度。
1.2.2定性指标
边坡的稳定与否,不仅取决于岩土体内部地质结构,也取决于外部环境因素的影响,是多种因素的综合作用。根据已有的研究结果[10]以及国家规范标准[11-13],遵循重要性、独立性和易测性的原则,同时考虑实际工程经验[14-15],结合边坡实际资料确定其定性指标隶属度取值见表1。
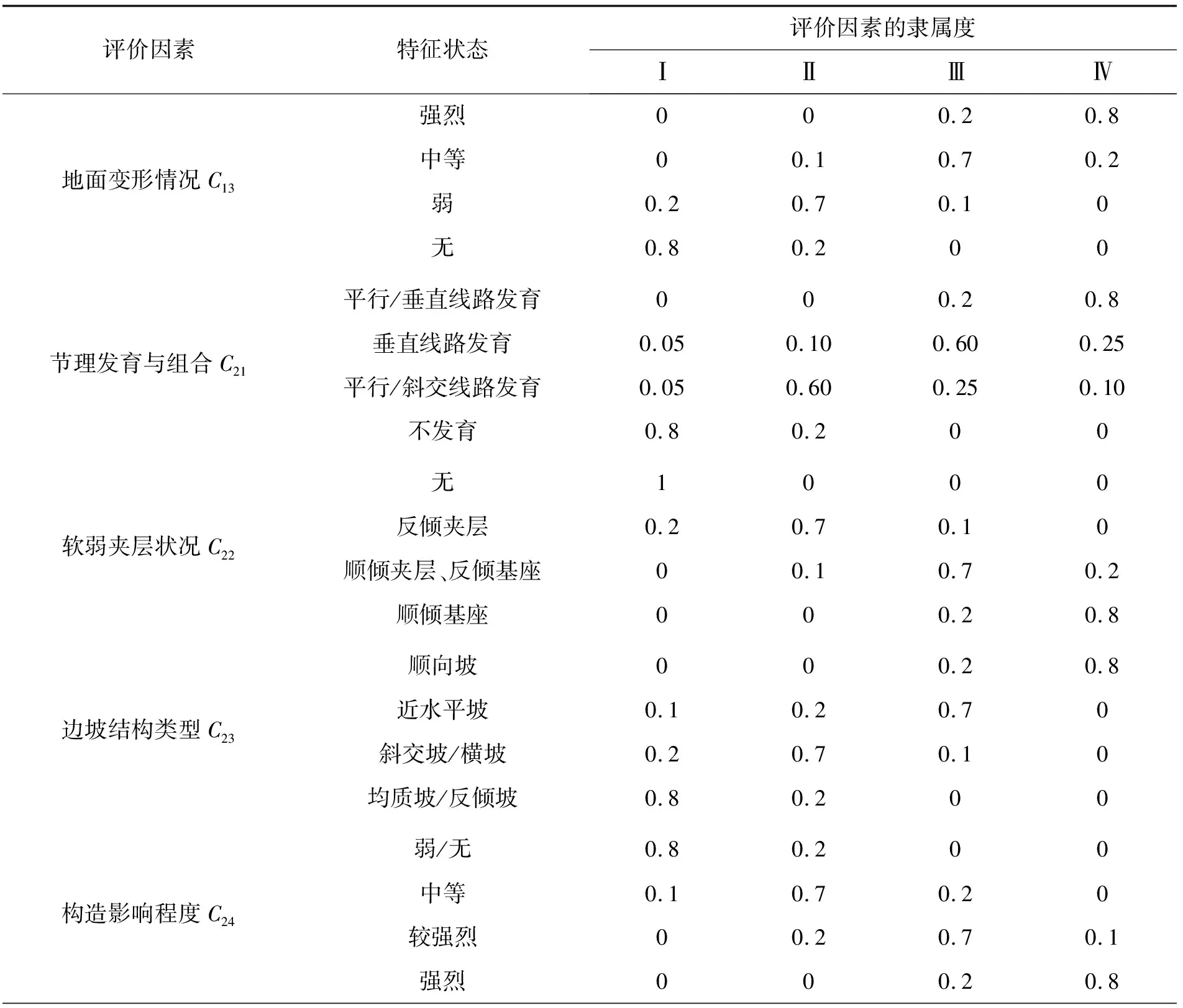
表1 定性指标隶属度取值
1.3 权重的确定
1.3.1层次分析法
层次分析法是目前计算主观权重的常用方法,广泛应用在解决复杂问题的决策分析方面,其具体的计算步骤如下。
a)根据实际情况建立层次分析结构模型。
b)构造判断矩阵[16-17]。根据目标层确定各因素之间相对重要程度,结合九段标度法(表2),构造两两比较的判断矩阵A见式(5)。

表2 重要性标度含义
(5)
式中aij——比例标度,表示同层次中第i个元素与第j个元素相比前者的重要程度。
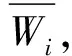
(6)
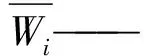

(7)
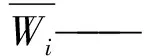
e)一致性检验[18]。依据公式AW=λmaxW,求出最大特征值λmax,进行一致性检验,见式(8)。
近年来,云计算因其具有高速的数据分析计算、数据共享、数据存储等服务,受到了各行各业的广泛重视,手机购物、支付、交易等都是通过云计算来实现的,云计算会自动分析出不同人群的兴趣点,并自动分别给他们推荐各自喜欢的不同商品,这样的服务给企业提供了创造价值的新思路;云计算还可以让企业能适时地获取网民对不同商品的关注数据变化情况。图1显示了微博的微指数产品对30天内网民对洗衣粉和洗衣液的关注数据对比情况,网民对洗衣液的兴趣度明显高于洗衣粉,云计算的应用具有巨大的商业价值。
(8)
式中λmax——判断矩阵最大特征值;CI——一致性指标;CR——一致性比率;RI——平均随机一致性指标,根据n不同取值见表3。
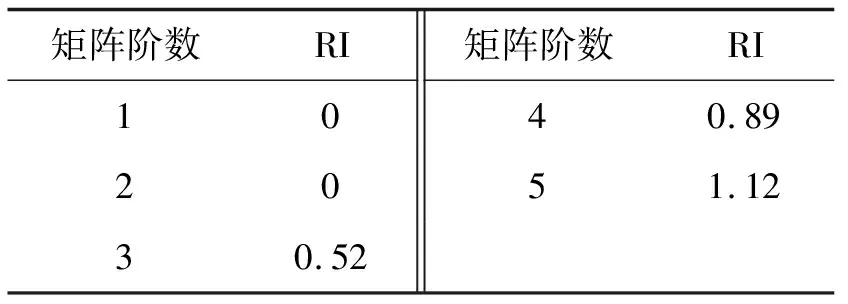
表3 平均随机一致性指标RI
当CR<0.1时,认为判断矩阵A具有满意的一致性,否则需要重新调整判断矩阵,重复上述步骤,直到满足一致性检验为止。
1.3.2熵权法
熵权法广泛应用于计算客观权重方面[19],主要依据客观资料对指标赋权,避免了因为主观人为因素的影响而导致赋权结果不准确的问题。其计算步骤如下。
a)设有m个评价对象、n个评价指标构成的模糊综合评价矩阵R=(rij)m×n,见式(9)。
(9)
式中i、j——第i个评价对象和对应的第j个评价值(i=1,2,…,m;j=1,2,…,n)。
b)计算第j项指标的熵值ej,见式(10)。
(10)
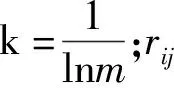
c)确定熵权,见式(11)。
(11)
博弈论又被称为对策论,是研究具有斗争或竞争性质现象的理论和方法。本研究就是通过博弈论的思想将主客观权重组合,进而得出最优组合权重[20],其具体的操作步骤如下。
a)构造可能的权重集。假设使用L种方法计算权重,可知其中任意的一个权重集合以及这些权重向量的任何线性组合构成一组可能的权重,见式(12)。
(12)
式中ω——最终的权重集的综合权重向量;βk——权重系数,且βk>0。
b)寻找最合理的权重向量。使用博弈论集结模型对L个权重集的权重系数βk进行优化计算,可以得到与各种权重分配方法协调、一致和平衡的组合权重结果,见式(13)。
(13)
式中ωg——第g种方式计算得出的权重集合。
c)求得最优组合系数。根据矩阵的微分性质,式(13)的最佳一阶导数条件见式(14),最终求得最优组合系数。
(14)
求出该解β=(β1,β2,…,βk),进行归一化处理,得出组合权重,见式(15)。
(15)
1.4 模糊综合评价
通过上述分析,假设已求出(1)中C1的4个二级指标的权重集合:W1={w1,w2,w3,w4},则C1指标的模糊综合评判结果B1为:
B1=W1R1
(16)
同理,可得其他3个一级指标的模糊综合评判结果B2,B3,B4,因此边坡综合评价矩阵为:
B={B1,B2,B3,B4}
(17)
组合赋权法求出4个一级指标的权重分配矩阵W,则最终评价结果为:
X=WB=(x1,x2,x3,x4)
(18)
通过最大隶属度原则xmax={x1,x2,x3,x4}得出相对于Ni={N1,N2,N3,N4}={Ⅰ,Ⅱ,Ⅲ,Ⅳ}的评价等级。
2 实例分析
2.1 工程概况
湖北兴山蒋家淌滑坡位于兴山县昭君镇大礼溪村,前缘因山体滑坡挤压,发生推移变形,侵占部分大礼溪河道,严重威胁到下方规划大礼溪工业园及当地居民的生命财产安全。根据现场调查确定其指标调查结果见表4。
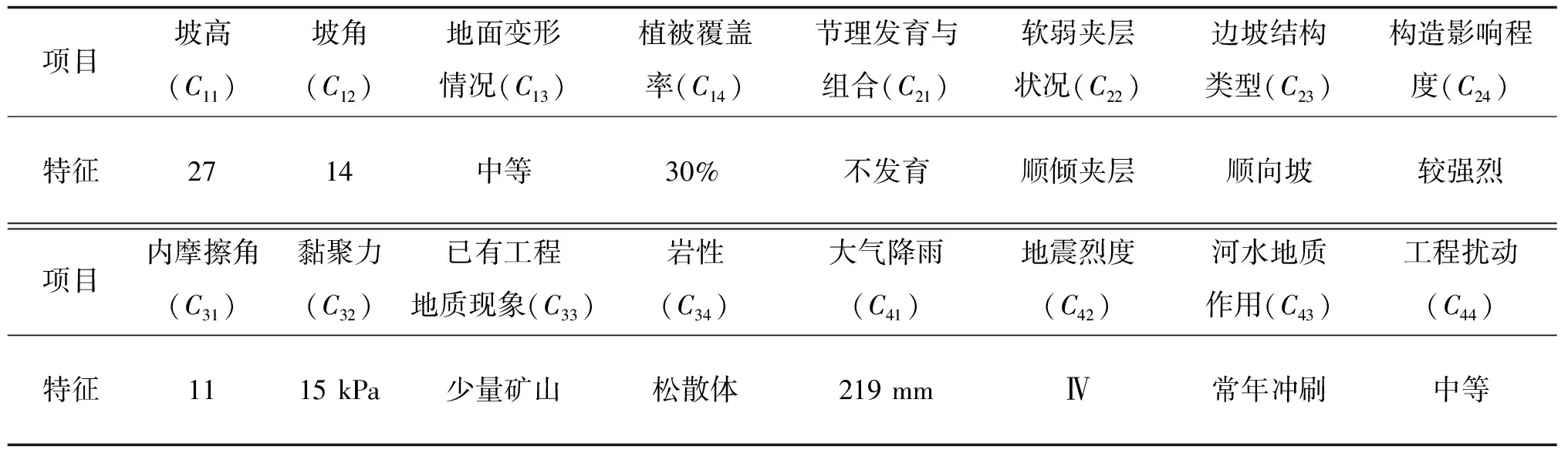
表4 蒋家趟滑坡稳定性调查结果
2.2 模糊综合评价
对C1、C2、C3、C44个一级指标进行两两比较,构造判断矩阵A。
(19)
由层次分析法中式(6)—(8)得4个一级指标的权重W=(0.115 0.239 0.592 0.054),CR=0.066<0.1一致性检验合格。
以一级指标C1为例,结合式(2)—(4),以及表1,可知C1的模糊评价矩阵R1为:
(20)
层次分析法确定权重为WC1=(0.245 0.483 0.192 0.080);由熵权法确定权重为WS1=(0.247 0.254 0.207 0.292);组合权重为W1=(0.245 0.458 0.194 0.103)。
由式(16)可知C1指标的综合评价结果为:
B1=W1R1=
(0.305 0.275 0.271 0.149)
(21)
其余二级指标权重计算结果见表5。
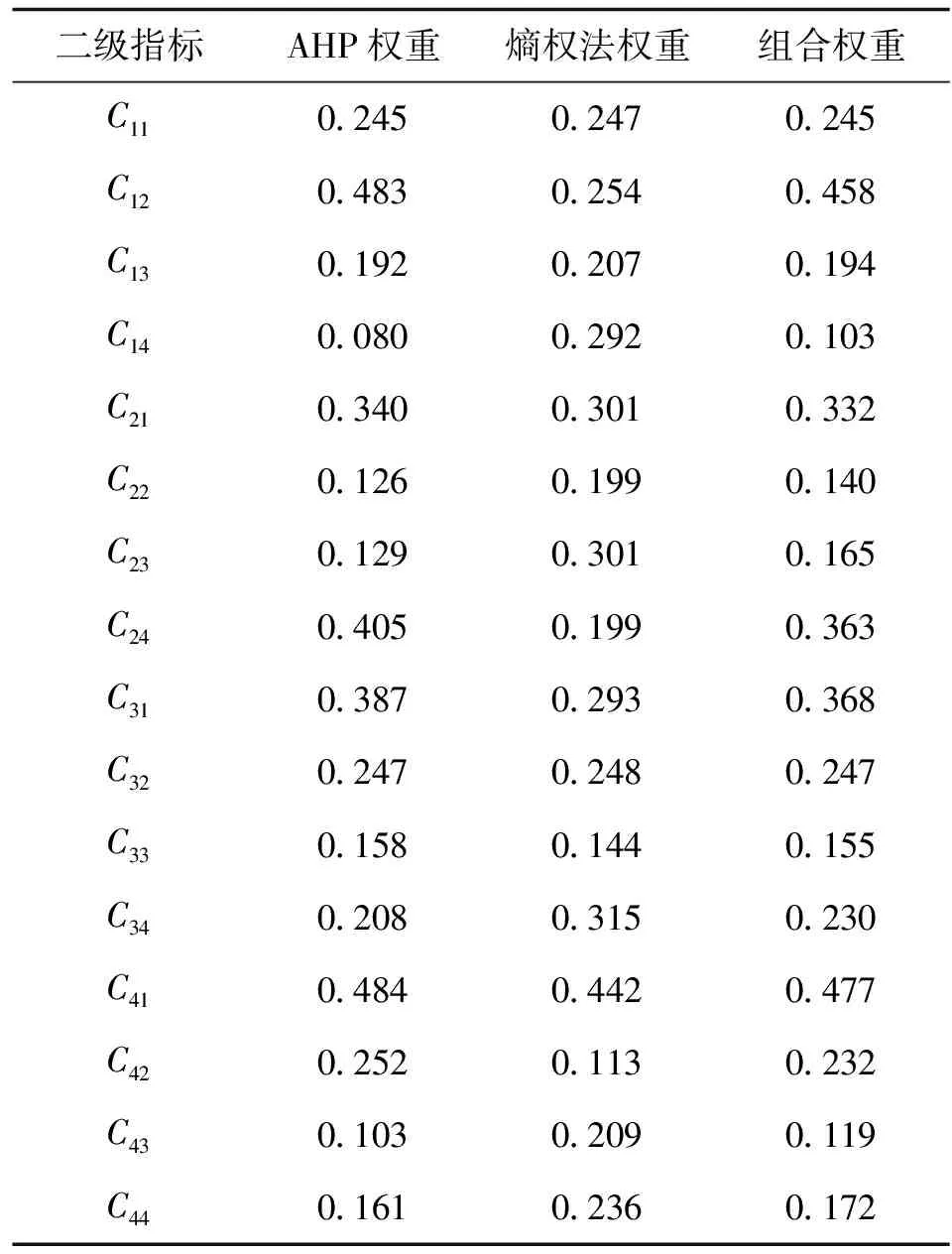
表5 蒋家趟滑坡稳定性指标权重
以相同方法计算其余3个一级指标评价结果B2、B3、B4后,由式(18)得该边坡模糊综合评价结果。
X=WB=
(0.129 0.080 0.304 0.487)
(22)
由最大隶属度原则可知xmax={0.129 0.080 0.304 0.487}=0.487,故蒋家趟边坡的稳定等级为第Ⅳ级,极不稳定,与实际情况相吻合。
2.3 结果分析
将分别采用层次分析法、熵权法、博弈论组合赋权法的计算结果进行对比(表6),可以看出3种方法计算结果均为“极不稳定”,与实际情况相吻合,但相比于单一的层次分析法或熵权法,采用博弈论组合赋权法的模糊评价结果介于层次分析法和熵权法之间,这是因为在博弈论组合赋权的过程中不仅考虑到了主观人为因素的影响,而且有效结合了客观实际情况,使得评价结果能较好地处理各单因素变化对稳定性的影响,评价更为合理。
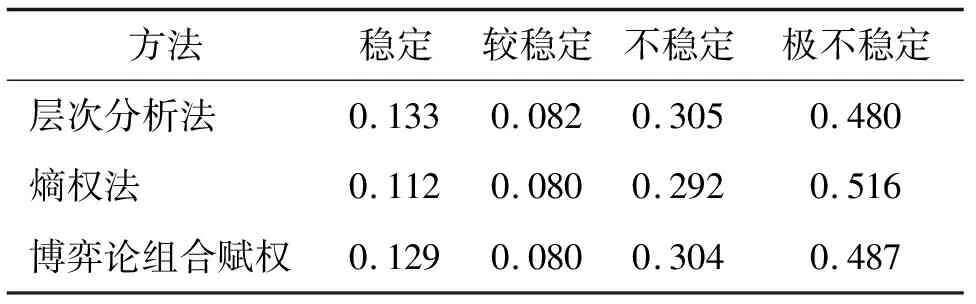
表6 评价结果对比
3 结语
a)在层次分析法和熵权法的基础上采用博弈论组合赋权法对边坡稳定性评价指标体系进行赋权,不仅考虑了主观人为因素的影响,还有效结合了客观实际情况,评价结果较单一赋权方式更合理。
b)构建了模糊综合评价体系,该模型理论易懂,计算简便,综合考虑了多种因素的影响,每个评价指标相对于不同的等级都有不同的隶属度,评价结果符合研究区的实际情况,可为边坡的稳定性评价提供一定思路和参考价值。

