分布式指挥条件下作战方案模糊优选方法

方 冰，韩 冰，付雪梅

（陆军指挥学院，南京 210045）

0 引言

现代战争是陆、海、空、天、电多维一体的体系化联合作战，战场态势瞬息万变，不确定性情况日益增多，传统集中式指挥模式难以适应如此复杂的战场环境。为有效应对复杂战场形势的挑战，快速响应战场态势变化，进而通过谋取决策优势来谋取行动优势。各指挥实体彼此之间通过网络化的指挥信息系统相连，共同实施指挥控制活动［1］。采用分布式指挥，指挥员可以虚拟召集所属指挥实体，综合运用指挥信息系统所提供的音频、视频、图文等多种手段，进行研讨交流、同步分析判断、谋划建议和评估优选作战方案。分布式指挥能够发挥充分指挥实体分散配置的优势，对战场态势的变化更敏感，相应的指挥实体有更强的“现场感”；同时，各指挥实体的决策环境相对独立，更易从专业的角度给出决策信息。

分布式指挥的执行实体不是单一层级，而是纵向上的多层。这些指挥实体在统一领导下，同步了解上级意图，同步分析判断情况，同步谋划决心建议，同步评估优选作战方案。与传统的集中式指挥相比，分布式指挥没有改变指挥内容，改变的是指挥信息的组织方式。指挥信息系统在作战中的广泛运用，使得多个指挥实体能够在异地同步共享战场态势信息，在分散配置的状态下，通过“虚拟集中”的方式参与指挥决策。分布式指挥能够有效控制指挥成本，显著降低指挥实体的暴露风险，符合信息化战场的内在逻辑要求。如何对分布式的指挥信息进行科学表述，如何对分布式指挥信息进行有效融合，进而快速达成群体共识，体现分布式指挥优势；成为分布式指挥需要考虑的首要问题。在分布式指挥条件下，各级各类指挥实体拥有较大的独立性，同时也背负更大的责任。因而，在分布式指挥条件下，作战任务的复杂性和战场环境的不确定性会给这些“相对独立”的指挥实体带来沉重的认知负担和心理压力，使他们在面对诸如作战方案优选、军事资源分配等核心决策问题时常常犹豫不决、举棋不定。

如何在统一的衡量标准下，准确建模各级各类指挥实体的决策信息，实现对多个备选作战方案的鉴别比较和优劣排序，进而快速达成群体共识，是谋取分布式指挥优势、实现联合制胜的关键环节［2］。本文通过将分布式指挥条件下的作战方案优选问题建模为概率犹豫模糊［3］环境下的多属性决策问题，构建分布式指挥信息融合方法，增加指挥者赋值的科学性和灵活性。在概率犹豫模糊元欧几里得距离测度［4］的基础上，建立了关于属性权重向量求解的线性规划模型，并给出了权重向量的解析解；在属性权重向量求解的基础上，分别基于传统的逼近理想点（Technique for Order Preference by Similarity to Ideal Solution，TOPSIS）算法［5］和前景理论［6-7］，给出了两种分布式指挥信息融合方法，实现了多个备选作战方案的优劣排序，达成了群体共识，整个论证过程清晰严谨、算法简明有效。

1 概率犹豫模糊集理论

2009 年，西班牙学者Torra 针对多属性决策（Multi-attribute Decision Making，MADM）问题中，决策者在给出决策信息时常常犹豫不决，以及多个专家互相不能说服、难以达成一致意见的情形，提出了犹豫模糊集（Hesitant fuzzy set，HFS）的概念［8-9］。犹豫模糊集的基本描述工具是犹豫模糊元（Hesitant Fuzzy Element，HFE）［10］，犹豫模糊元是一个由多个实值构成的集合，表示相应的评估对象具有几个可能隶属度。然而，犹豫模糊元不能刻画决策者对不同隶属度信息的偏好程度，从而导致对不确定信息性的非完整性描述。为更加准确地描述决策者的评估不确定性，徐泽水等学者于2017 年提出了概率犹豫模糊集（Probabilistic Hesitant Fuzzy Set，PHFS）的概念［4-5］，进一步拓展了模糊决策理论。概率犹豫模糊集的基本描述工具是概率犹豫模糊元（Probailistic Hesitant Fuzzy Element，PHFE）［11-12］。与犹豫模糊元相比，概率犹豫模糊元在犹豫模糊元的基础上，同时给出了每个隶属度可能发生的概率信息，进而包含了更多的不确定性信息。

2 概率犹豫模糊环境下的决策模型

2.1 多属性决策问题描述

2.2 权重向量求解

总体上，希望每个方案和正理想解间的加权距离应尽可能小。同时，由于各个备选方案是公平竞争的，不存在任何特殊的偏好关系。因此，可以等权相加的方式建立如下的线性规划模型来求解属性权重向量w

显然，式（14）和式（11）所表示的线性规划问题是等价的，且为典型的凸优化问题，具有唯一最优解［15］。对问题（14）进行求解，需要构造如下的拉格朗日（Lagrange）函数

实际上，在构建权重向量求解模型时，人们通常会根据不同的应用背景，对指标权重施加不同的限制条件。此时，没有通用的解析方法可以使用，但是可以使用数值方法进行求解，如CVX 优化工具包等［16］，此处不再赘述。

2.3 基于TOPSIS 的排序算法

2.4 基于累计前景理论的排序算法

前景理论是以“有限理性”为前提，反映决策者的主观风险偏好［6-7］，决策者依据参考点来衡量各个方案的收益和损失情况。若以正理想点1˜（p）为参考点，则各概率犹豫模糊元相对于参考点来说都是损失的，其前景价值可以计算为

3 算例分析

3.1 问题描述

作战方案优选是作战指挥的关键环节和定下决心的基础，作战方案的优选过程也是群体共识的达成过程。通常，对一种作战方案的优劣评价，要看其3 种属性：一是方案可行性，作战方案是否符合上级意图，能否在限定的时间、空间及其他资源条件下完成作战任务；二是方案可接受性，作战方案是否完整、要素齐全，能够取得的潜在价值是否大于实施方案需要付出的代价，包括政治代价与道义代价；三是方案独特性，作战方案是否符合战术运用原则、切合战场实际，与其他方案相比有显著不同，体现较大的艺术创造性。

评选出最优作战方案，可以为正确定下战斗决心奠定必要基础。假定有4 个指挥组{b1，b2，b3，b4}（指挥实体的分组情况由最高指挥员根据战场实际需求确定）受命对4 种作战方案{x1，x2，x3，x4}进行分析评估，并给出专业化建议。这4 个指挥组通过方案可行性a1，可接受性a2和独特性a3这3 种属性，分别对4 种备选作战方案进行评估。如前所述，指挥组对备选方案各属性的评估结果，以概率犹豫模糊元的形式给出。表1～表3 分别表示4 个指挥组的评估结果，为便于比较分析，本文所用数据改编自文献［3］和文献［13-14］。

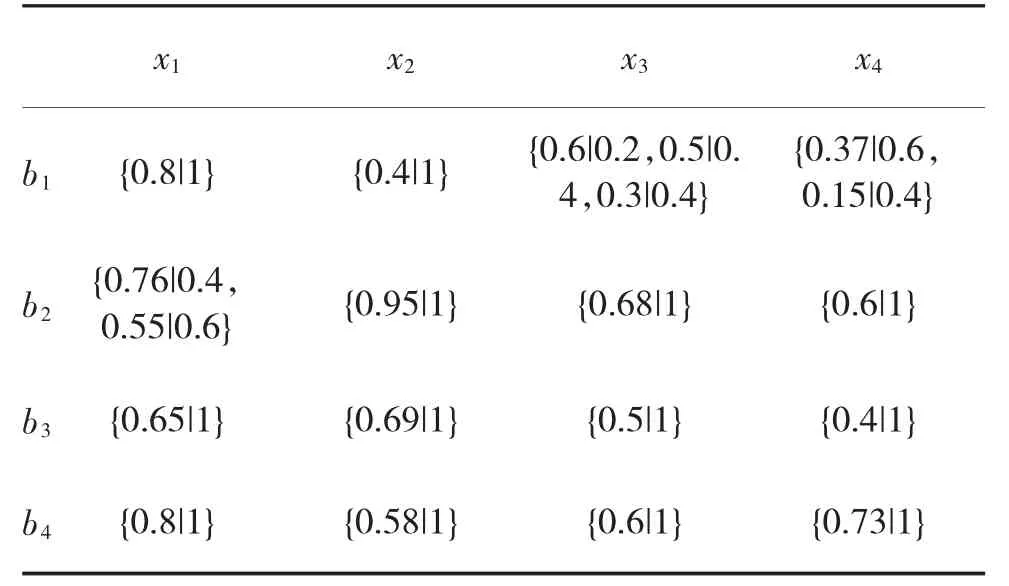
表1 备选方案可行性（a1）评价结果

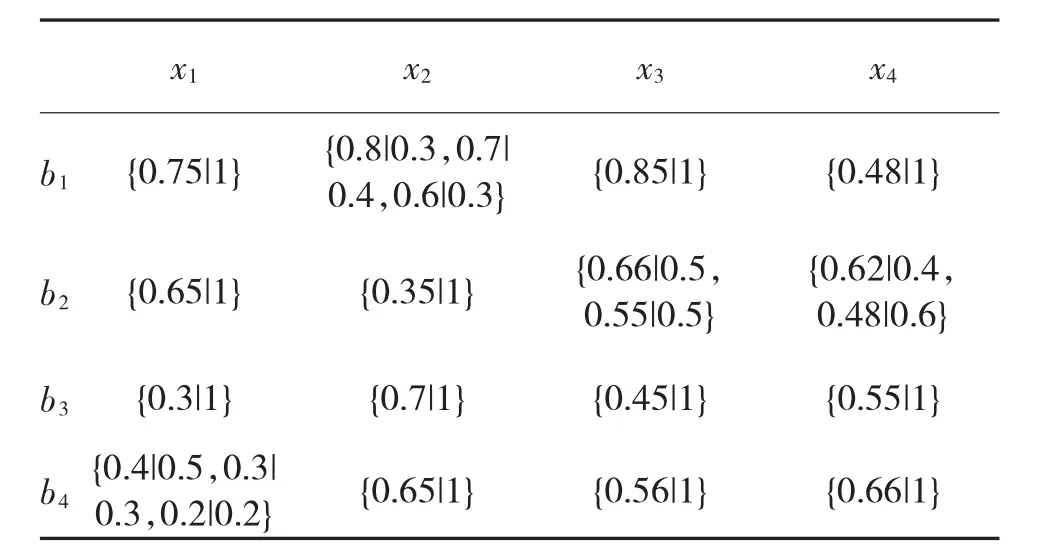
表2 备选方案可接受性（a2）评价结果

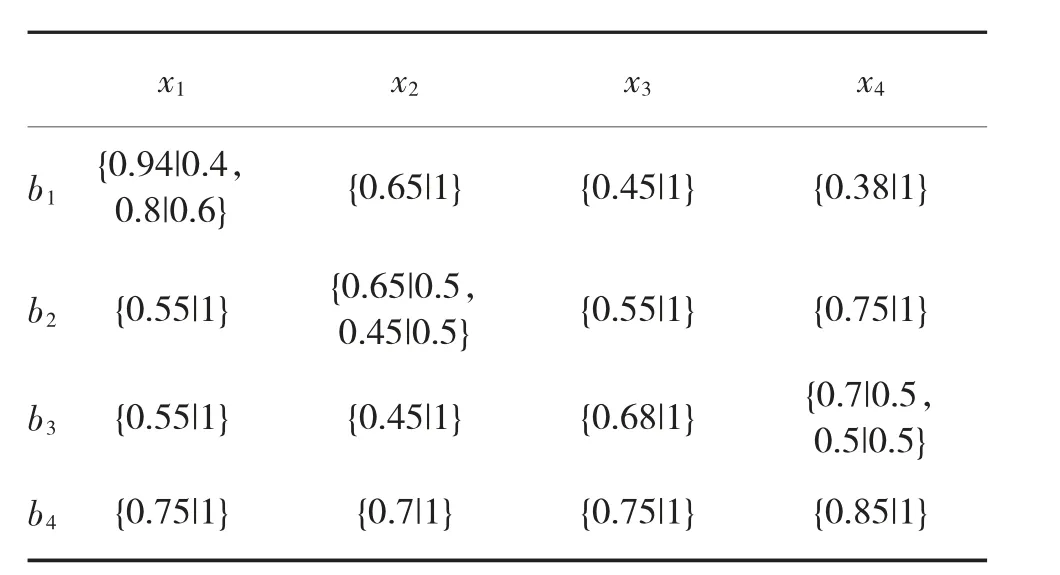
表3 备选方案独特性（a3）评价结果

3.2 指挥组意见聚合

假设这4 个指挥组的权重相同，即这4 个指挥组的权重均为0.25。根据表1 及全概率公式，这4个指挥组对备选作战方案x1关于属性值a1的评估意见可以聚合为

也 即 为 概 率 犹 豫 模 糊 元{0.8|0.5，0.76|0.1，0.65|0.25，0.55|0.15}。同理，根据表1～表3，这4 个指挥组的意见可以综合为概率犹豫模糊决策矩阵A，如表4 所示。

表4 概率犹豫模糊决策矩阵（A）

3.3 确定属性权重

3.4 方案排序：方法1

3.5 方案排序：方法2

根据2.4 节所述的排序算法，本节按照以下4个步骤对备选作战方案进行优劣排序：

Step 1：根据式（22）和表5，取参数α=β=0.88，θ=2.25，计算备选方案{x1，x2，x3，x4}各属性的负前景值，如表7 所示。

表5 各方案属性值到正理想点的距离集{}

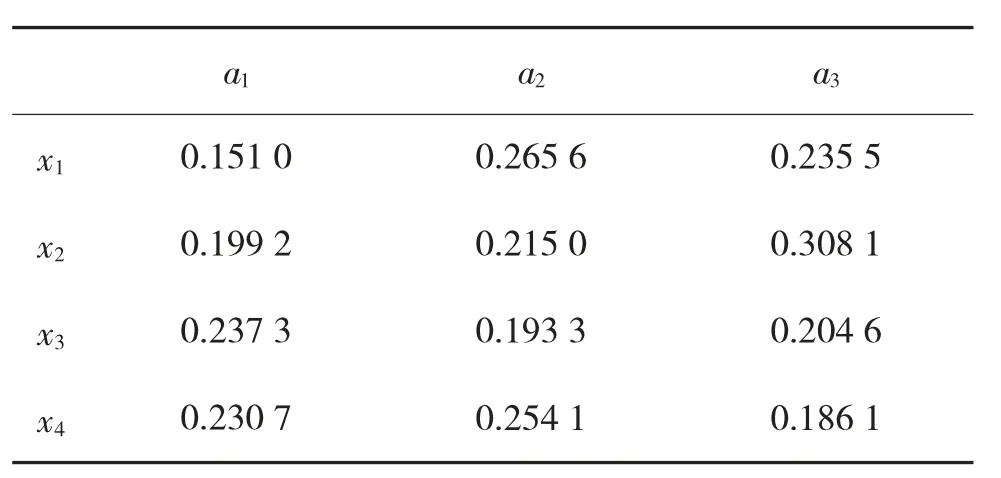
表5 各方案属性值到正理想点的距离集{}

?

表7 备选方案各属性值的负前景值{}

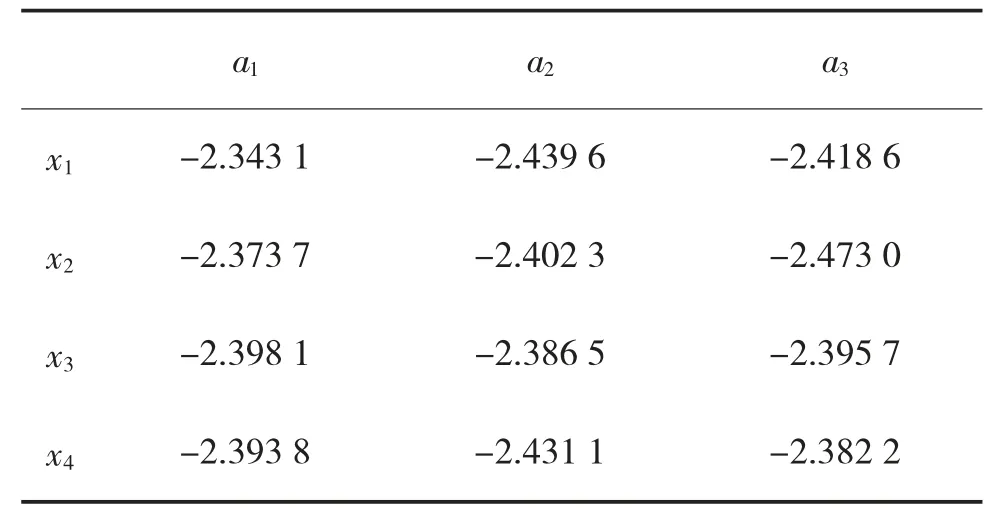
表7 备选方案各属性值的负前景值{}

?

Step 2：根据式（23）和表6，取参数α=β=0.88，θ=2.25 计算备选方案{x1，x2，x3，x4} 各属性的正前景值，如表8 所示。

表6 各方案属性值到负理想点的距离集{}

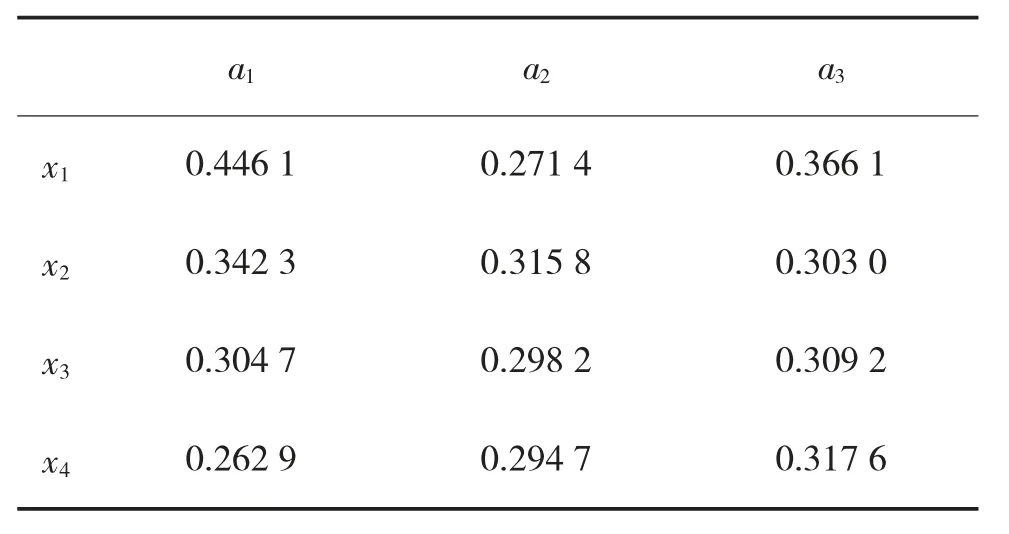
表6 各方案属性值到负理想点的距离集{}

?

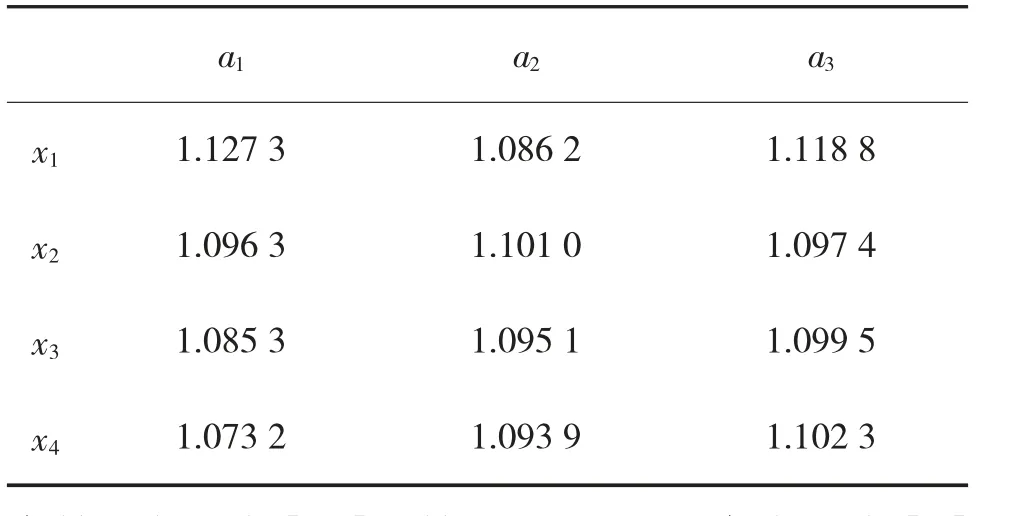
表8 备选方案各属性值的正前景值{vij}

3.6 比较分析

为对本文方法的有效性进行说明，这里对同一算例的计算结果与其他文献方法的所得结果相比较，如表9 所示。显然，本文采用的两种方法得到排序结果与文献［14］的结果是一致的，但与文献［3］的排序结果存在一定差异，其主要原因是文献［3］使用的属性权重向量为w=（0.2，0.5，0.3），与本文有较大差异。

表9 不同方法的决策结果

通过与文献［3］和文献［14］的求解过程相比较可知，本文采用的信息融合方法更为简单，且计算过程易于理解；也能够根据一些场景的特殊需求来重新构建权重向量求解模型，而不影响信息融合方法的整体架构，具有较大的灵活性和可扩展性，更易产生令人信服的结果。

4 结论

作战方案优选是指挥决策的关键环节和正确定下决心的基础，作战方案的优选过程也是群体共识的达成过程。本文通过将分布式指挥条件下的作战方案优选问题建模为概率犹豫模糊环境下的多属性决策问题，为分散配置的指挥实体快速达成共识提供了适宜的决策框架和信息描述工具，所构建的分布式指挥信息融合方法，有助于充分发挥分布式指挥的优势，积极应对信息化战场挑战。