基于两阶段优化模型的海上横向补给规划研究*

董 鹏，黄佳帅，石怀斌

（海军工程大学管理工程与装备经济系，武汉 430033）

0 引言

随着我国海上权益的进一步主张，海上军事力量建设的重要性日益凸显，舰艇编队作为海上军事力量的直接体现，为其提供有效的后勤保障不可或缺。因此，合理规划海上补给过程，提高海上补给效率，具有重要意义。

目前，海上横向补给规划的研究有很多，张泉先等人［1］利用海洋气象信息，建立了基于时长步进的算法模型，对战时存在补给时间窗情况下的舰船编队海上补给路径进行了规划。文献［2-4］通过采用一种改进旅行商问题，构建了横向补给的路径规划的数学模型，通过蚁群算法进行求解，从而对单补给舰的编队海上补给路径进行了优化。秦芙蓉等［5］针对巡回牧师策略下的海上补给规划问题建立模型，运用启发式算法求解最优补给路径。周晓光等［6］根据网络流理论，分别将横向补给的3 种补给策略进行了数学描述，并将3 种策略下的优化结果进行对比。王城超等［7-8］通过预测接收舰船的补给时间窗，构建最小化补给时间的整数规划模型，分别通过改进遗传算法与C-W 算法修正后的动态规划方法进行求解，对多补给舰情况下的编队海上补给路径进行优化。Brown 等［9］通过二维的坐标输入以及谷歌地球的信息共享，以路径优化为目标，以作战舰艇的最低物资需求补给为约束条件，通过使用整数规划以及启发式算法进行求解。根据文献的整理，在现有的海上补给组织架构下，考虑物资的特殊性及其出入库时间的物资补给顺序优化问题研究较少。

本文采用多智能体与整数规划模型相结合的方法，通过多智能体系统的信息传递及相互协作，解决海上物资补给过程中的物资排队问题，通过整数规划模型准确计算海上补给的舰船补给顺序。

1 海上横向补给情况分析

横向补给是航行补给的一种海上补给方法，指的是舰船在航行状态下，补给舰与接收舰保持横列编队，通过舰船上的横向补给装置对补给舰及接收舰进行连接，进行物资的传送。横向补给是航行补给方式中目前应用最广的方法，本文也以横向补给作为研究对象。

1.1 横向补给策略

编队补给中，由于舰队行进过程中都保持着特定的战位，舰与舰之间的距离和方向也都有着明确的规定，因而横向补给出现了3 种常见的补给策略，即送报男孩策略、加油站策略、巡回牧师策略，如图1 所示。其中，送报男孩策略（以下简称DB 策略），由于操作简单，且可以最大限度地保持舰艇编队的整体作战阵型，应用最为广泛，是本文的研究对象。该策略下，补给舰暂时离开原有的战位，按照既定的补给次序，依次驶向各艘接收舰位置进行补给，接收舰保持特定的航向及航速行进。

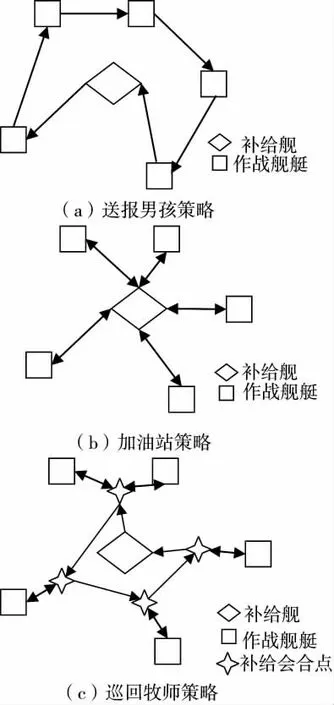
图1 海上横向补给策略

1.2 横向补给特点分析

横向补给过程需要执行接收舰或补给舰向补给阵位航行、架设、撤除传送装置等作业，这部分作业会消耗一定比例的时间，在实际的补给过程中，为了提高补给效率，减少补给装备架设等作业的重复，在物资数量能够满足所有接收舰物资需求时，实际补给作业中，会选择将当前接收舰的所有物资需求都补充完毕后，再进行下一艘接收舰的物资补给，因而可以将单艘接收舰的物资补给顺序和编队内的接收舰的补给顺序分步骤进行研究，先求解单舰的最优物资补给顺序，再将物资补给顺序带入整体模型中，求解接收舰最优补给顺序，从而将横向补给规划转换为两阶段优化问题。

1.3 补给目标分析

海上补给作为维持海上力量的根本途径，其战略意义突出，同时其被敌对力量海上打击优先级也处于前列，在不考虑飓风、暴雨等极端自然情况下，可以将海上补给所处外界环境分为平时环境及战时环境。

平时环境下，由于既不存在敌对力量对补给进行干扰和打击，又不考虑海况等自然环境因素，因而不存在外界因素会影响补给进程，海上补给除了文中所考虑的排队情况以外，不存在其他情况使补给进入等待状态，所有的补给需求都能够被满足。这种环境下，不同补给方案实施的最大区别就在于实施补给所消耗的时间长短，因此，平时环境下通过衡量时间成本要素来评价运输方案的优劣，本文以最小化的补给完成时间为平时环境下的补给目标。

在战时环境下，由于海上补给进程会被敌对力量的袭击所打断，而且由于敌袭时间的随机性，补给需求能够被全部完成的可能性较小，因而需要对补给物资及舰船进行优化。由于战场环境复杂多变，且无法获取实际数据，为了便于建立研究模型，对战时情况采取简化处理，在不考虑敌方打击顺序和我方战斗损失的前提下，假设作为约束条件的补给中断时间已知，同时考虑战时环境中作战效能的重要性，本文将最大化补给的边际作战效能作为战时环境的补给目标。

2 海上横向补给模型构建

2.1 单舰物资补给多智能体仿真模型

在平时的补给规划中，通过构建单舰物资补给仿真模型，求解平时情况下的单舰物资补给顺序。根据单舰物资运输仅需对物资出库、物资运输、载具返回、物资入库4 个环节进行仿真的特点，以及海上补给多目标接收舰的实际情况，分别建立“补给舰”单一智能体、“接收舰”智能体群。

2.1.1 “补给舰”智能体

“补给舰”智能体，主要完成物资出库作业以及协同“接收舰”智能体完成物资运输作业。“补给舰”智能体设置有各类物资出库速率、各“接收舰”物资需求等参数，设置有甲板物资数量、目标接收舰、运输顺序、补给完成数量、出库物资数量、当前运输物资、当前出库物资等变量。“补给舰”智能体根据其需要实现的行为及判断，设置有甲板状态图，甲板工作状态图，物资运输状态图，运输判断状态图4个状态图。甲板状态图，负责判断甲板物资数量是否达到“补给舰”甲板容量上限，造成甲板拥堵。甲板工作图，负责物资的出库作业。物资运输状态图，负责协同“接收舰”智能体完成物资运输作业。运输判断状态图，负责通过检查“接收舰”甲板是否产生拥堵，判断是否能够进行物资的运输［10］。

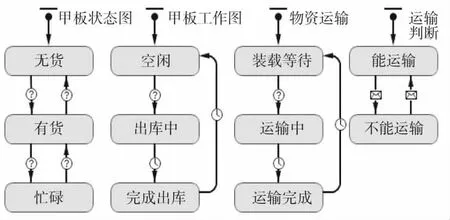
图2 “补给舰”智能体状态图

2.1.2 “接收舰”智能体

“接收舰”的智能体群，主要负责协同“补给舰”智能体进行物资运输作业及物资的入库作业。“接收舰”智能体设置有各类物资入库速率参数，设置有当前运输物资、当前入库物资、甲板物资数量、物资入库排列等变量。“接收舰”智能体根据其需要实现的行为及判断，设置有甲板工作图、接收状态图及补给状态图。其中甲板工作图，负责物资的入库作业。接受状态图，负责接收“补给舰”发送的运输物资信息。补给状态图，负责判断甲板物资数量是否达到甲板容量上限，导致补给进程暂停，并将消息传递给“补给舰”智能体［10］。

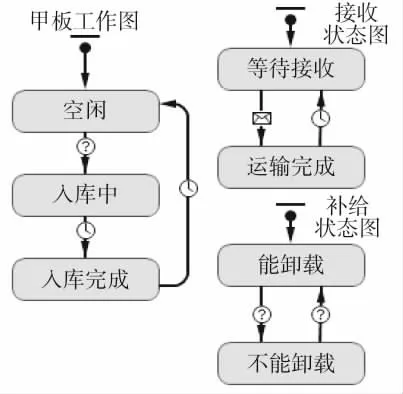
图3 “接受舰”智能体状态图

在战时的补给规划中，由于补给时间的限制，为了最大化作战效能，引入“效时比”的概念，通过计算效时比=作战效能/（出库时间+运输时间+入库时间），将每艘接收舰的需求物资进行效时比排序，优先补给效时高的物资，从而得出单舰的物资运输顺序，再将其带入整体仿真模型中，求解具体时间限制下的最优补给顺序。

2.2 平时情况下海上横向补给数学模型

平时情况下，海上补给规划目标为尽快满足舰艇编队的物资需求，即海上补给总时间最小，因为接收舰始终未离开自身补给阵位，因而定义补给总时间为自补给舰离开自身舰位开始，至最后一个轮次物资在接收舰上入库完成为止所消耗的总时间。

根据补给过程分析，设定如下参数变量：

其中，式（1）表示补给目标函数，补给总时间最小；约束条件式（2）表示每一补给轮次只补给一艘接收舰；约束条件式（3）表示一次补给作业中，一艘接收舰仅能被补给一次；式（4）表示每一轮次补给时间的计算，由两部分组成，分别为补给舰前往补给阵位的航行时间以及补给舰对当前接收舰进行物资补给的时间。式（5）～式（6）表示补给舰位置随着补给轮次改变而相应地变化，第1 轮次开始前补给舰位置就在其初始位置，第1 轮之后的其他轮次补给开始之前，补给舰位置就是上一轮次接收舰所在位置，因为DB 策略下的海上补给，接收舰相对位置不发生改变，补给舰前往各个接收舰相对位置进行补给，其当前轮次补给结束的位置即下一轮次补给开始的位置与当前的接收舰坐标一致。

2.3 战时情况下海上横向补给数学模型

战时情况下，出于作战的需求以及敌袭的影响，海上补给目标为限定时间内通过补给规划，使得补给生成的边际作战效能最大。边际作战效能为补给一个批次物资，引起总作战效能的增加值。

在上文设置的变量基础上，追加设定以下参数与变量：

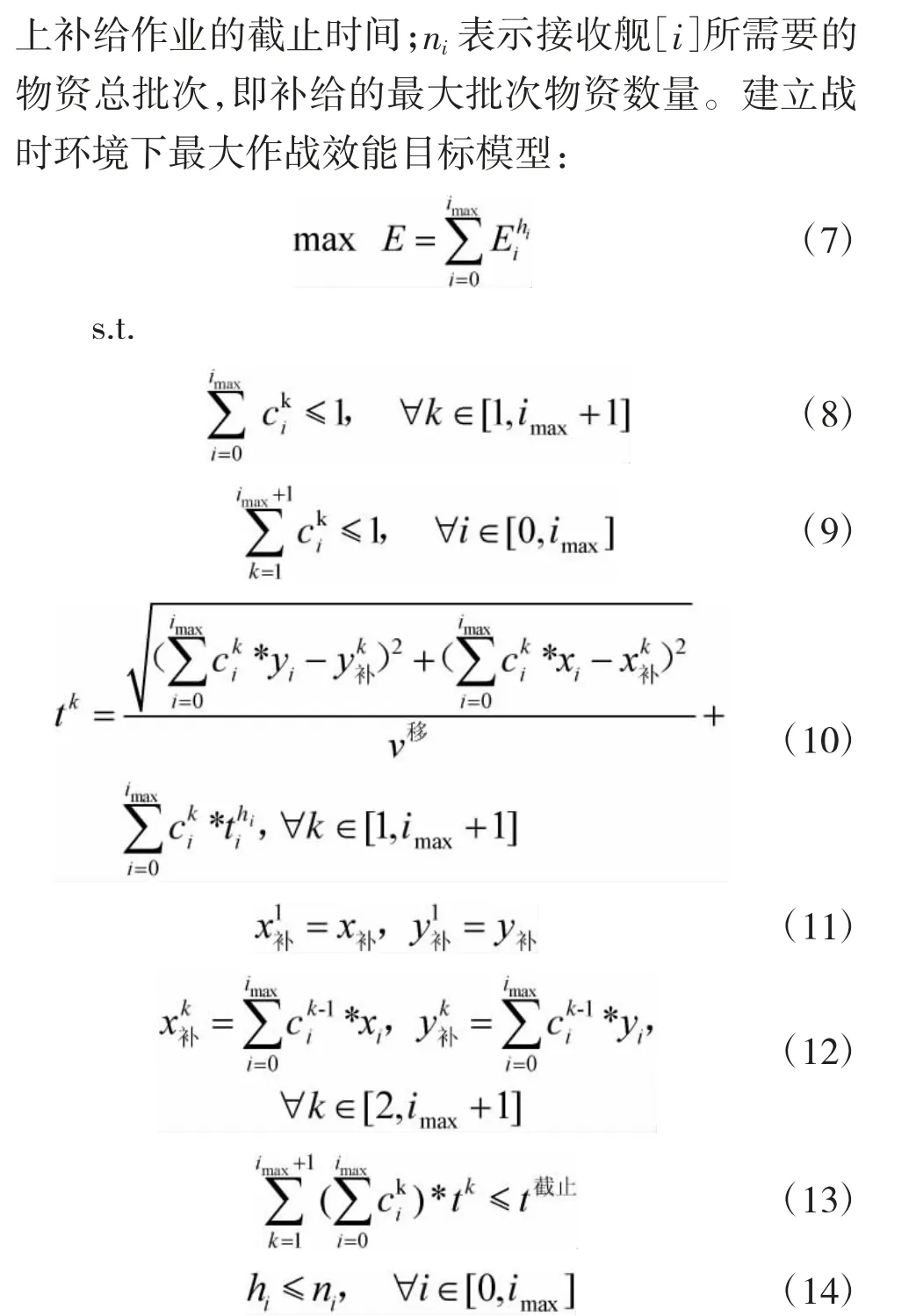
其中，式（7）即为战时情况下的目标函数，即限定时间内海上补给作业生成的边际作战效能最大；约束式（8）表示每一轮次最多只会补给一艘接收舰；约束式（9）表示在一次海上补给连续作业中，一艘接收舰最多只能被补给一次；式（10）表示每一轮次补给时间的计算，为补给舰前往补给阵位的航行时间，以及补给舰对当前接收舰进行物资补给的时间求和；式（11）～式（12）表示随着补给轮次的变化，补给舰位置的更新；约束条件式（13）表示补给的总时间不得超过截止时间；约束条件式（14）表示每一艘接收舰的补给截止轮次不得超过其物资总需求。

3 算例分析

任务设定一个海上舰艇编队，有一艘补给舰进行伴随补给，携带有4 种补给物资，编号物资［1～4］，各物资出入库速度已知，且在当前作战方案下的作战效能值已知；编队内有6 艘作战舰艇需要补给，编号接收舰［0～5］，需要寻找出平时补给时间最短目标下的补给顺序，以及特定时间下作战效能最大目标下的补给顺序。为了方便衡量作战效能，物资计量单位为横向补给运输批次，横向补给一次载具运输作业所能够运输的物资量即为一批次物资，作战效能为每类物资每批次边际作战效能，物资的出/入库速度计量单位统一为min/ 每批次物资，即每批物资出/入库所需要多少分钟。编队内的各接收舰所需物资数量如表1 所示，合计需要59批次的物资。

表1 物资需求表

补给舰初始位置设定为（300，300），4 类物资的出库速度为（7.5，10，20，12），补给舰甲板物资容量设定为4 个批次物资。

接收舰位置信息，4 类物资的入库速度、作战效能如表2 所示，各个接收舰的甲板物资容量都设定为2 个批次物资。

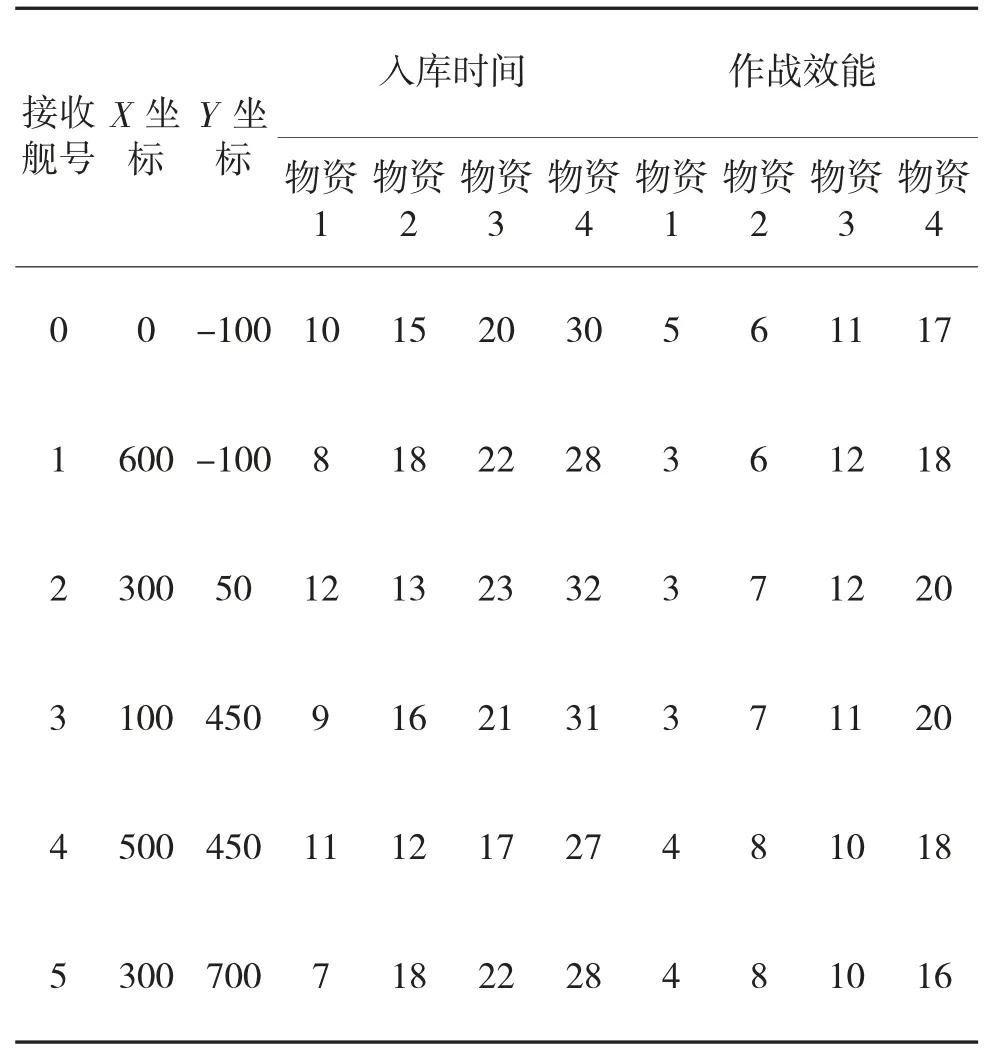
表2 接收舰信息

物资计量单位为横向补给运输批次，即横向补给一次运输所能够运输的物资量，物资在传送装置上的运输时间统一为15 min，带入单舰物资补给多智能体模型，求解平时情况下的每艘接收舰的补给时间最小的最优物资补给顺序。

通过参数变化实验，对补给时间最小化目标下的每艘接收舰最优物资补给顺序进行求解，实验结果显示每艘接收舰的最优物资补给顺序并不唯一，这里仅展示其中一个最优解，结果如下所示。

接收舰［0］：补给完成所需要补给的最小时间为175.133 min，补给物资顺序为{物资［1］，物资［1］，物资［4］，物资［1］，物资［3］，物资［2］，物资［1］，物资［3］，物资［1］}。

接收舰［1］：补给完成所有物资需求最小时间为246.15 min，补给物资顺序为{物资［物资［2］，物资［3］，物资［2］，物资［3］，物资［3］，物资［4］，物资［4］，物资［3］，物资［4］，物资［1］}；

接收舰［2］：补给完成所需要补给的最小时间为277.167 min，补给物资顺序为{物资［1］，物资［3］，物资［3］，物资［3］，物资［4］，物资［4］，物资［2］，物资［4］，物资［4］，物资［2］，物资［2］}；

接收舰［3］：补给完成所有物资需求最小时间为258.15 min，补给物资顺序为{物资［2］，物资［3］，物资［2］，物资［2］，物资［3］，物资［4］，物资［4］，物资［4］，物资［4］，物资［1］}；

接收舰［4］：补给完成所需要补给的最小时间为209.067 min，补给物资顺序为{物资［1］，物资［1］，物资［4］，物资［1］，物资［4］，物资［2］，物资［3］，物资［2］，物资［2］，物资［2］，物资［2］}；

接收舰［5］：补给完成所需要补给的最小时间为165.083 min，补给物资顺序为{物资［2］，物资［2］，物资［2］，物资［3］，物资［2］，物资［4］，物资［1］，物资［1］}。

求解战时情况下的每艘接收舰的物资效时比顺序，计算结果如表3 所示。

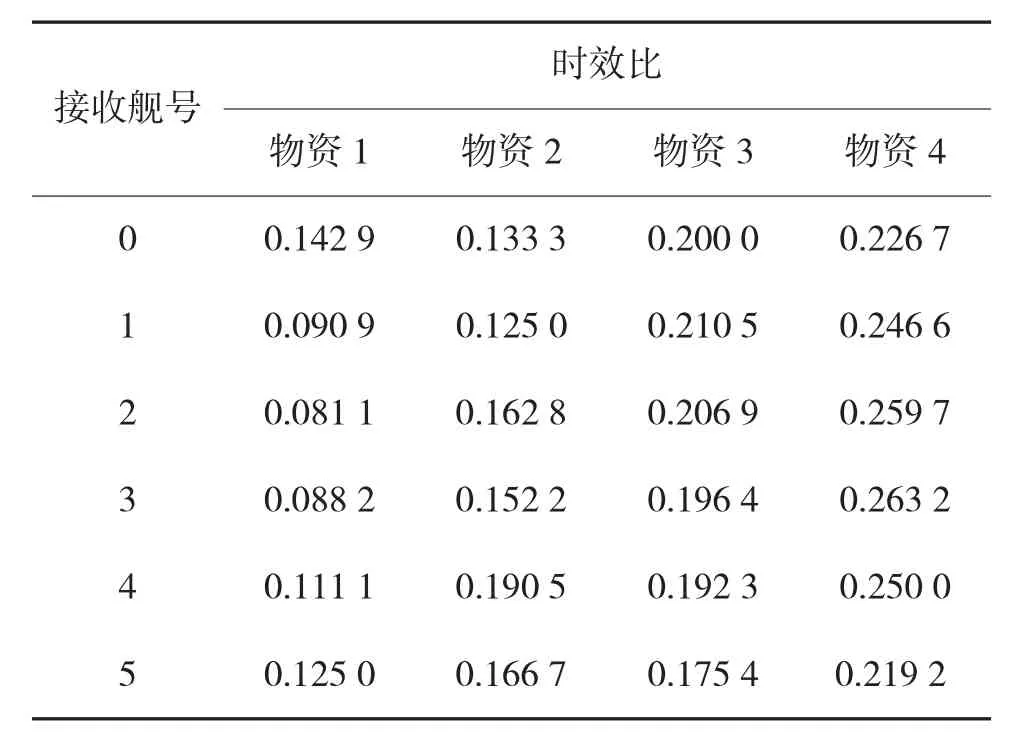
表3 物资效时比

根据表3 所示，接收舰［0］的物资效时比排序由高至低分别为{物资［4］，物资［3］，物资［1］，物资［2］}，接收舰［1～5］的物资效时比排序由高至低分别为{物资［4］，物资［3］，物资［2］，物资［1］}。

根据物资效时比的物资排序，可以得出单艘舰艇进行海上补给的物资出库顺序，即物资效时比由高至低顺序，带入单舰物资补给仿真模型，可以得出每艘接收舰根据效时比物资排序进行运输的每一批次物资所耗费的出库时间、总运输时间及生成的边际作战效能，分别记为出，，，结果如表4所示。

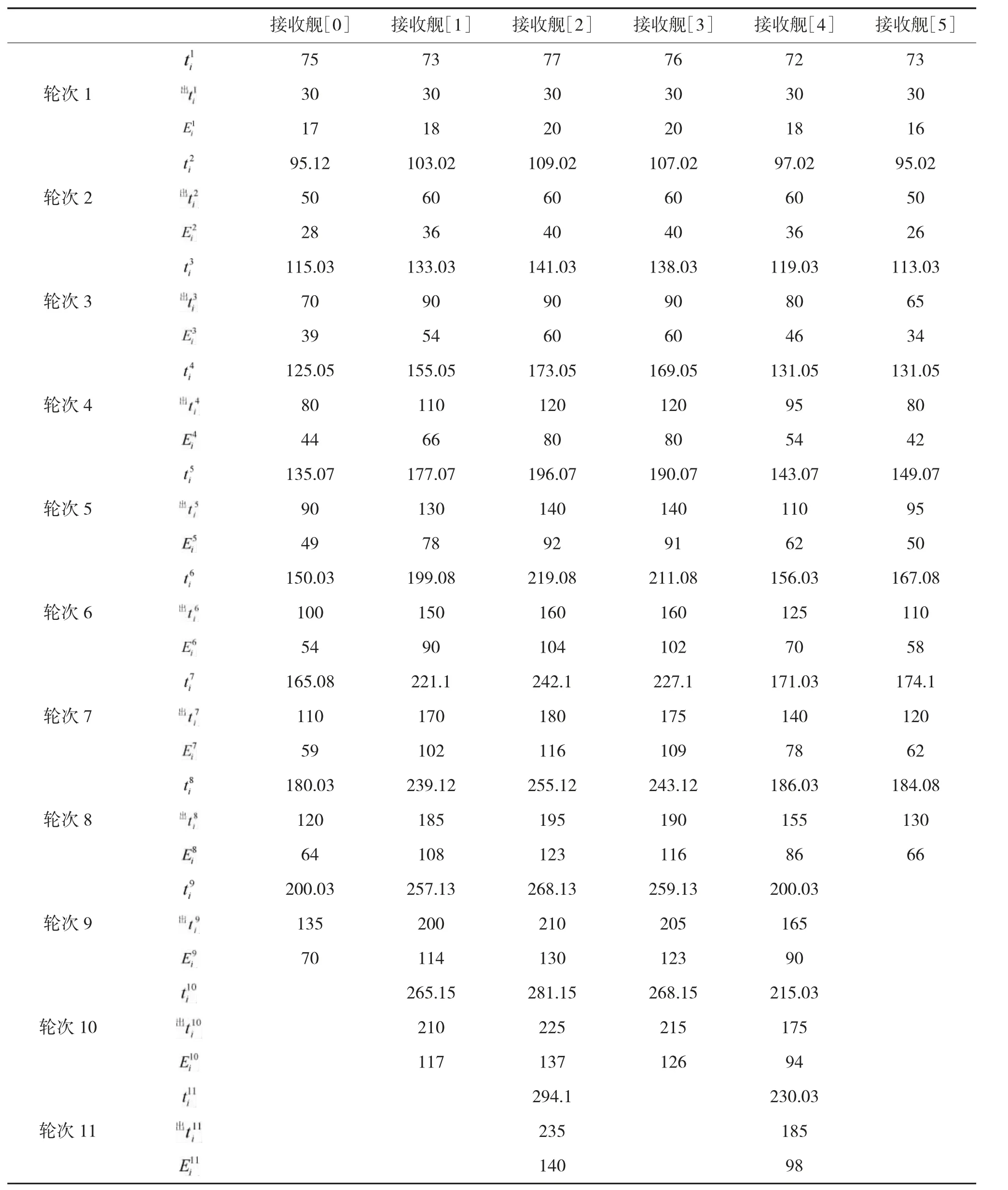
表4 各接收舰补给轮次信息

将单舰物资优化结果分别带入平时、战时整数规划模型，利用LINGO11.0 平台运算。平时环境下，采用DB 策略进行海上物资补给，补给完所有物资需求所需最小时间为1 472.093 min，补给顺序由前至后分别为接收舰［4］、接收舰［5］、接收舰［3］、接收舰［0］、接收舰［2］、接收舰［1］，物资补给顺序即为上文中所求各舰的单舰物资补给顺序。

战时环境下，采用DB 策略进行海上物资补给，700 min 时通过海上物资补给能够达到的边际作战效能增加值最大为320 效能值，舰船补给顺序由前至后分别为接收舰［4］、接收舰［2］、接收舰［3］，在有限的时间内，为最大化补给作战效能，仅对3 艘接收舰进行补给，补给的物资数量分别为接收舰［4］补给7 批次物资，接收舰［2］补给11 批次物资，接收舰［3］补给6 个批次物资。

结果可得，通过将海上横向补给转换为两阶段海上补给规划问题，利用多智能体模型以及整数规划模型能够有效进行求解。

4 结论

本文通过分析海上横向补给的作业特点，将海上横向补给问题转换为两阶段补给规划问题，通过多智能体模型与整数规划模型，对横向补给方案进行了优化，有效提高了横向补给效率。但本文还有部分不足，两阶段模型分别采用不同的建模手段，利用不同的仿真软件运算，给数据转换输入带来了困难；战时仅通过限定时间来反映出战时环境的约束，并不能够完全体现出实际情况。