基于CEEMDAN和小波阈值去噪的混合积分位移算法
胡 超,毛宽民,张东峰,周嘉诚
(1.宁夏大学,宁夏银川 750021;2.华中科技大学,湖北武汉 430074)
0 引言
随着现代机械工业的发展,很多领域迫切需要位移测试技术不断更新。利用加速度传感器采集的加速度信号通过二次积分的方法,理论上能够得到真实的位移信号。然而,在加速度传感器收集振动信号的过程中,会受到自身设备及工况环境的影响,使得采集到的加速度信号包含噪声。与此同时,设备的温度变化等原因也会引入一定程度的低频噪声。使得加速度信号两次积分后的位移信号漂移严重,信号毛刺较多。因此,为得到完整可用的位移信号,对加速度积分位移信号算法的研究很重要。
积分方式分为时域积分和频域积分两种。误差趋势项及直流分量是影响时域积分效果的主要因素,普遍的处理方式是先对加速度信号进行去除均值处理,而后运用梯形法、Simpson法等积分规则进行一次积分得到速度信号,上述过程重复一次后即可得到位移信号,同时利用最小二乘法对趋势项进行多项式拟合,以达到减小信号漂移的目的。除了应用最小二乘法多项式拟合外,使用差分法、低通滤波法、最小均方法[1]等也可减小误差。
陆凡东等[2]利用经验模态分解(EMD)法对加速度信号的低频和高频部分分别进行了处理,实现降噪去趋势项的目的。同时,对有明显漂移的分量采用分段最小二乘法(SLS)进行处理。陈海龙等[3]提出一种基于EMD分解理论的积分误差分离方法,可以有效处理积分误差。仲志丹等[4]提出将自适应噪声的完备集合经验模态分解(CEEMDAN)自适应降噪和极点对称模态分解(ESMD)去趋势项相结合,有效区分了噪声分量与有效分量的分界点,为去除信号趋势项及噪声误差提供了新的方法。
在频域积分的过程中,低频信号的幅值误差将被放大,高频信号的幅值误差将衰减。要保证频域积分的效果,关键在于控制低频误差的影响。许多学者对频域积分算法进行研究。Brandt等[5]对多种积分算法进行对比,发现设计的低频截止算法对于低频噪声过滤效果较好,同时操作简单。Yun等[6-7]运用误差最小化方法,通过推算加速度位移积分控制方程,得到传递函数的频响表达式,引入趋势项控制因子实现低频衰减积分算法,从而对位移趋势项进行误差控制。该算法对积分过程控制精度较高,但计算量偏大。胡玉梅[8]等在低频衰减算法的基础上,对积分精度误差控制方程进行了优化处理,并研究了积分参数的选择对该算法积分效果的影响。
本文提出一种基于CEEMDAN与小波阈值去噪的混合积分算法,对实测信号进行预处理。通过先时域积分后频域积分的方式,降低高低频噪声及漂移误差对积分效果的影响。利用仿真方法分析了该算法的可行性,并搭建振动筛试验平台进行测试分析,采集加速度与位移信号,验证了本算法的有效性。
1 自适应噪声的完备集合经验模态分解与小波阈值去噪
1.1 自适应噪声的完备集合经验模态分解
经验模态分解(EMD)是一种利用三次样条曲线拟合局部极值,将信号通过包络线算法分解,提取其局部特征即本征模态分量(IMF)的方法,广泛应用于处理非线性、非平稳信号。由于算法存在局限性,EMD分解易出现模态混叠及端点效应[9]。集合经验模态分解(EEMD)则是基于EMD分解的基础上,添加均匀分布的白噪声用于抵消模态混叠现象。基于自适应噪声的完备集合经验模态分解(CEEMDAN)在保留EMD、EEMD的完备性、分量调制性的同时,解决了EEMD加入白噪声后引入的重构误差问题。CEEMDAN同时还具有一定的自适应性[10-12],输入参数简单,能够控制迭代时间,具体算法步骤如下:
(1)向周期为T的原始信号a(t)中加入高斯白噪声ωi(t),构造出新信号a′(t)=a(t)+βiωi(t),其中βi为噪声控制系数。利用EMD方法将新信号分解出I个IMF分量并求平均值,得到:
(1)
及一阶残差分量:
r1(t)=a(t)-IMF1(t)
(2)
(2)假设EMD分解后的第j个模态函数的算子为Ej(·)。则对信号r1(t)+β1E1(ωi(t))继续进行分解,经I次重复后,得到:
(3)
(3)由步骤(1)和(2)的计算过程,可推得第K阶的残差分量为rk(t)=rk+1(t)-IMFk(t),定义得到第K+1个模态分量为
(4)
(4)重复步骤(3),直到残差信号不能再继续分解,最终即可得到K个模态函数分量IMFk(t),最终的残差分量为
(5)
原始信号为
(6)
1.2 小波阈值去噪
小波变换是非平稳信号处理的常用方法之一。通过选择小波基,在尺度上进行伸缩、平移,能够从信号的全貌中看到细节。小波阈值去噪是运用小波变换,在选择合适的小波基和分解层数的基础上,设置阈值函数及临界阈值进行去噪,随后进行重构得到去噪后的信号。小波基及阈值函数可依据信号本身特点择优选取。
使用本文算法对试验采集的信号处理后发现,选用sym6小波进行5层分解,采用固定软阈值效果较理想。固定软阈值函数为:
(7)
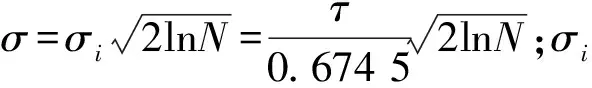
2 基于CEEMDAN和小波阈值去噪的混合积分位移算法
2.1 预处理部分
CEEMDAN及小波阈值去噪能够对趋势项及噪声进行很好的区分筛选。CEEMDAN算法将复杂的非平稳信号分解为多个本征模态函数IMF及残余信号,同时能够将IMF分量按照频率高低进行排列,如式(6)中:IMFk(t)为K个本征模态函数;R(t)为残余信号,即原信号中的趋势项。
在时域积分之前,先对各个IMF分量去除趋势项R(t)处理,然后去除信号的直流成分,即去均值化处理:
(8)
对分解得到的各个IMF分量进行去均值化及去趋势项的低频处理后,还需进行高频去噪处理。此时,需对IMF分量进行筛选,筛选IMF分量的方法有很多,可以通过自相关系数法、相关系数法等来判断IMF与原信号的相关性。一般计算出相关系数图后,对于相关系数小于0.1的分量即判断为伪分量。相关系数大于0.1的IMF分量中,当出现第1个局部极大值前的IMF分量为噪声主导的分量,然后对噪声主导的IMF分量进行小波阈值去噪[13-14]。上述分解去趋势项、去均值及去噪过程完成之后,将IMF分量进行重构即可得到预处理后的加速度信号。
2.2 混合积分部分
本文采用Simpson法对处理后的加速度信号x(i)进行一次时域积分得到速度信号y(k),N为采样点数,积分规则如式(9)所示:
(9)
在进行频域积分之前,需要利用最小二乘法对时域一次积分得到的速度信号进行多项式拟合,降低频域积分造成的影响。所使用的多项式拟合公式如下:
(10)
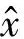
采用低频截止法对拟合后的速度信号进行二次积分。低频截止法是在频域积分过程中对信号的低频误差部分加以控制,即在频域积分过程中引入函数φ(ω):
(11)
频域积分过程可表示为
(12)
式中:fT为低频截止频率;F(·)为傅里叶变换;F-1(·)为傅里叶逆变换。
低频截止法频域积分的关键在于对低频截止频率的选择上。φ(ω)函数能够将信号的低频部分置为零,以保证积分过程中低频信号误差不会影响到积分效果。同时,低频信号所包含的信息也将被清零。低频截止频率的选择需要根据信号特点进行分析选取,一般要小于被测信号的第1个峰值。
混合积分完整流程,如图1所示。
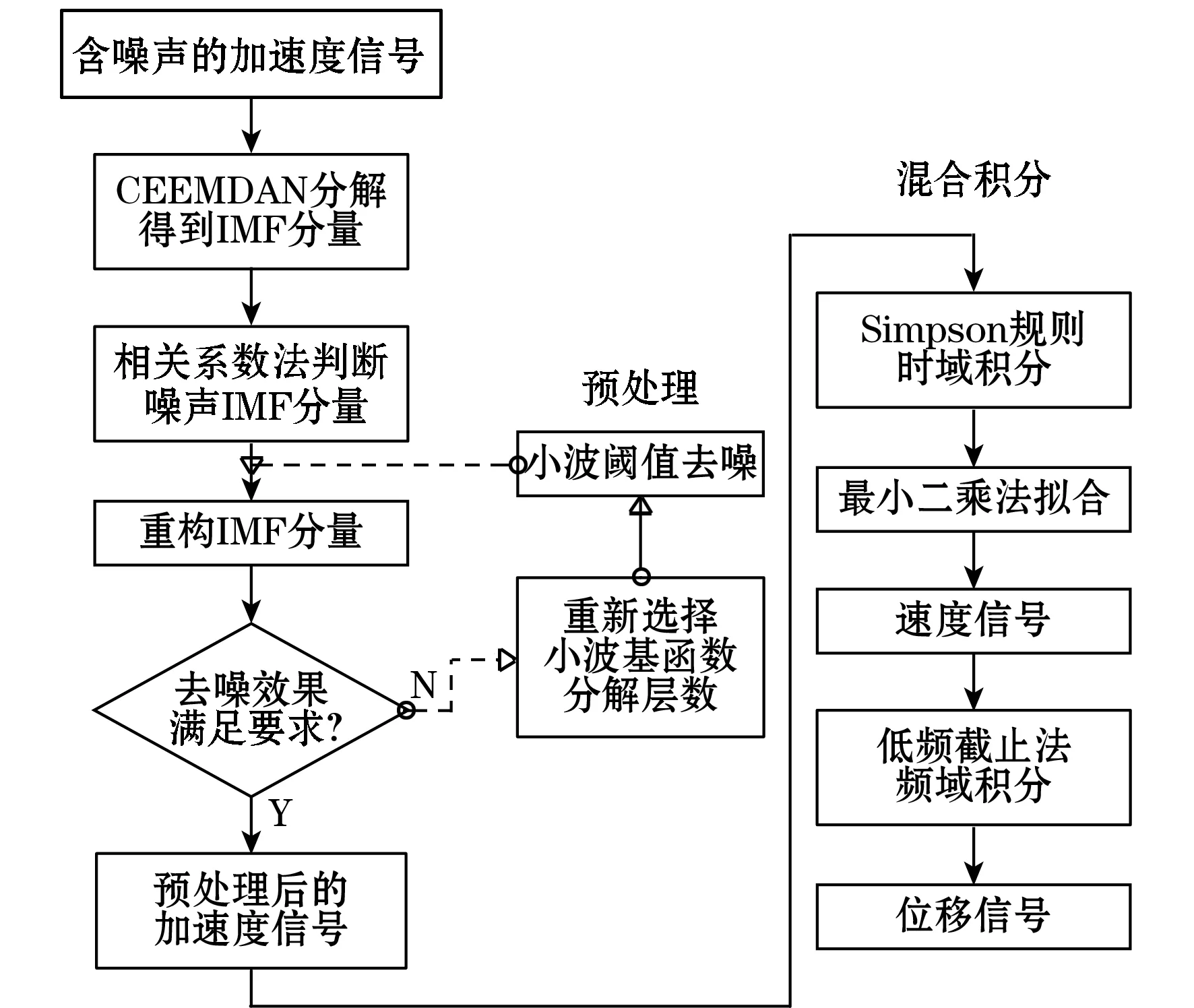
图1 混合积分算法流程图
3 仿真分析与试验验证
3.1 仿真分析
为验证本文混合算法的可行性,以Matlab为仿真软件,采用谐波加速度信号进行仿真分析。选取信号的采样频率为1 000 Hz,采样点数为1 000,组合谐波加速度信号为
a(t)=8sin(20πt)+25sin(50πt)+30sin(90πt)
对上式两次积分后即可得到对应的位移信号为
利用Matlab为加速度信号加入一定程度均匀分布的随机高斯白噪声,原加速度信号及加入高斯白噪声的加速度信号对比如图2所示。
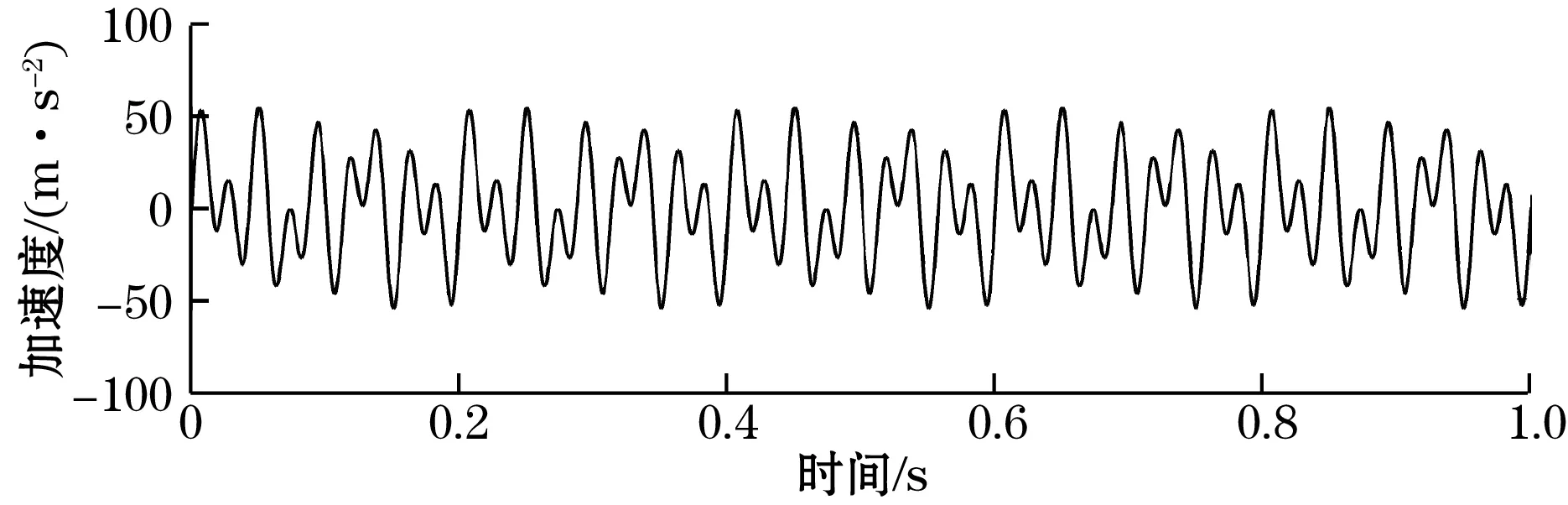
(a)未加入随机白噪声
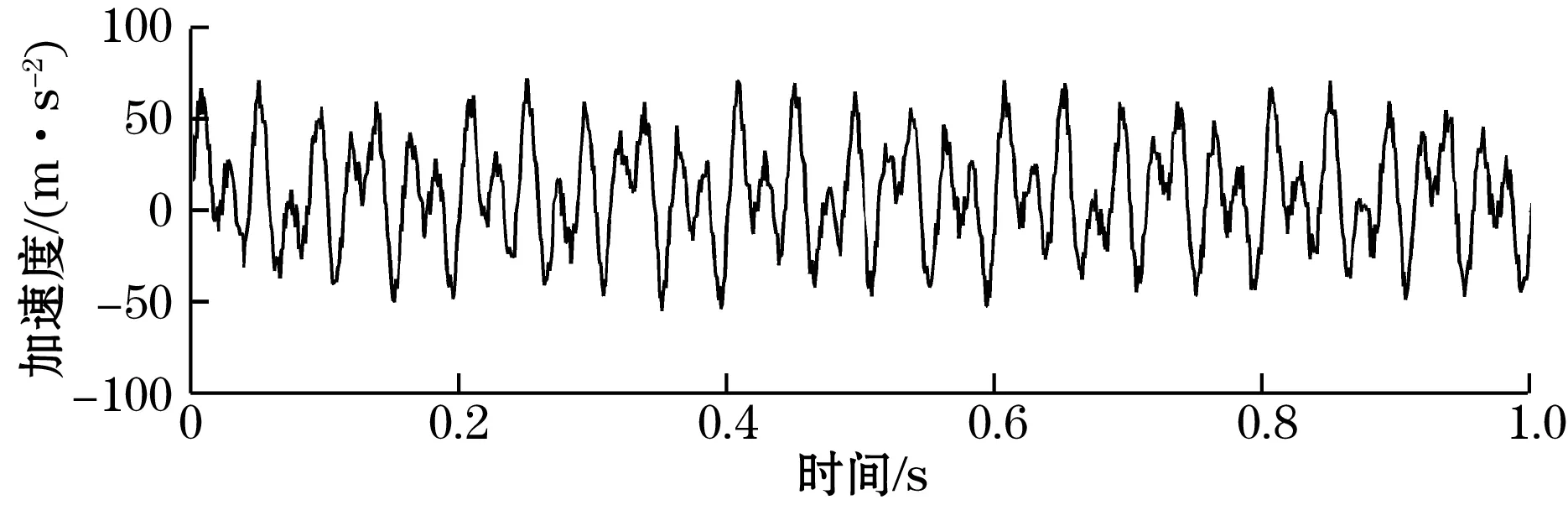
(b)加入随机白噪声图2 加噪前后加速度信号对比
对加入高斯白噪声的加速度信号进行CEEMDAN分解,得到IMF分量及趋势项。部分IMF分量如图3、图4所示。CEEMDAN分解所得到的趋势项分量如图5所示。
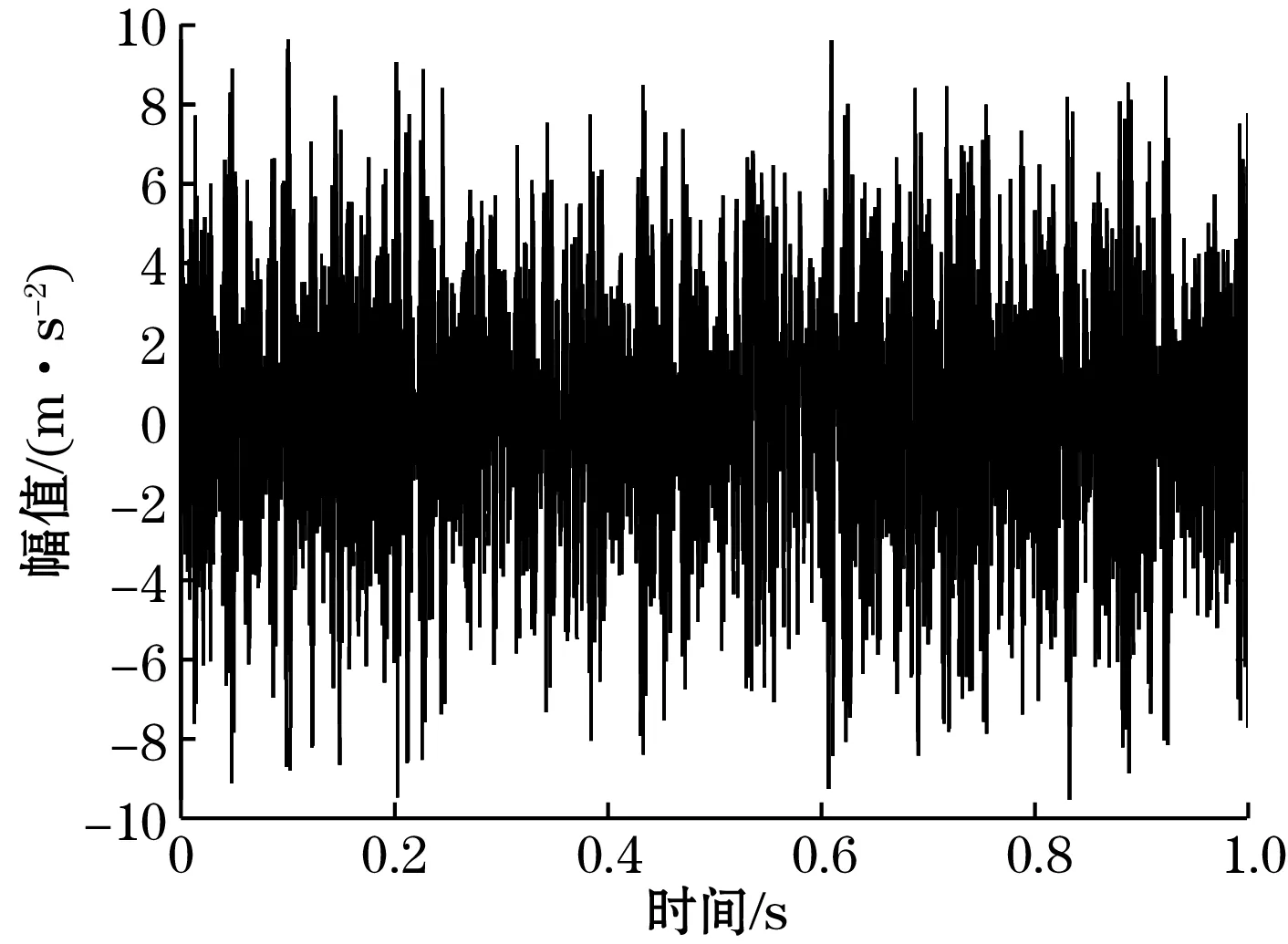
图3 IMF1分量
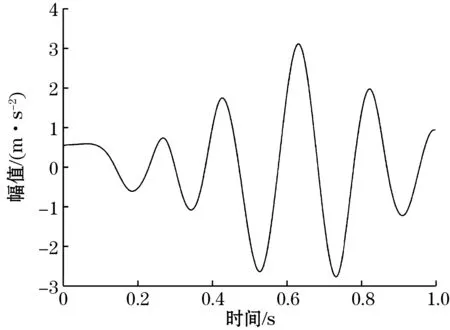
图4 IMF6分量
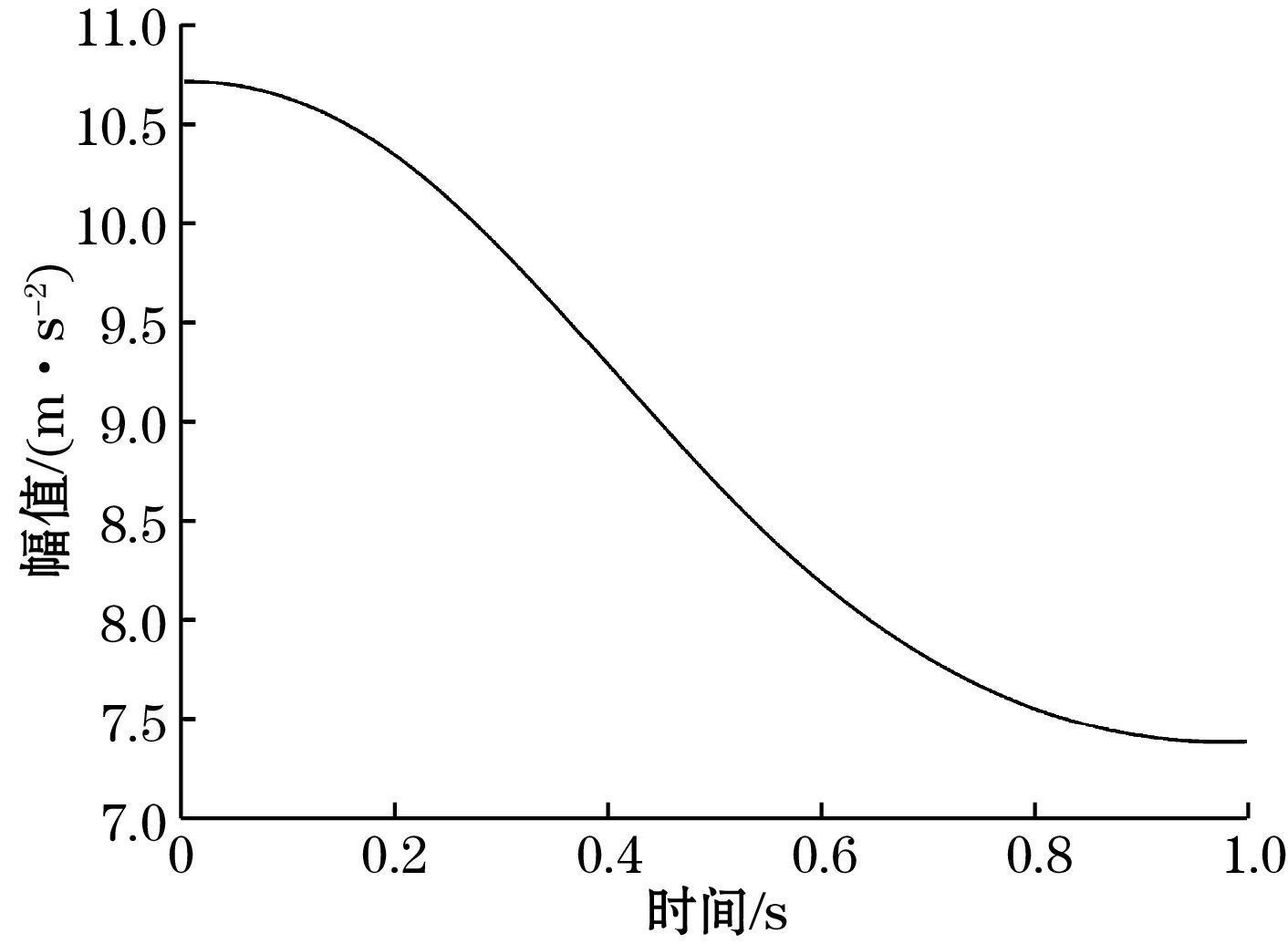
图5 IMF8分量
利用式(13)计算各个分量的相关系数,得到的相关系数如图6所示。
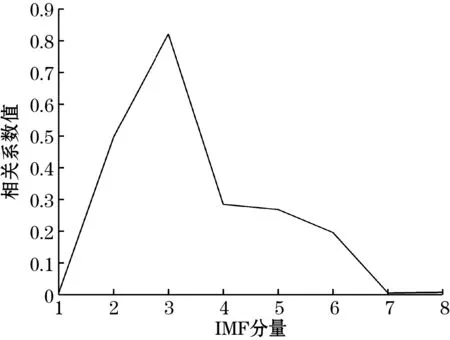
图6 相关系数图1
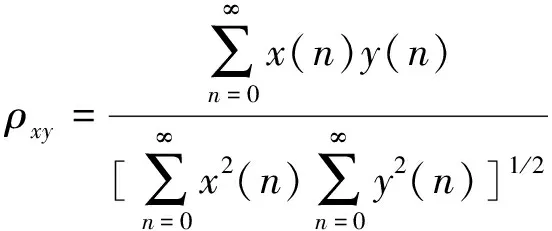
(13)
式中:x(n)、y(n)为时间序列相同的信号。
由于CEEMDAN的自适应性,能够将IMF分量从高频到低频进行排列。从相关系数图可以看出,相关系数先升高后降低,IMF1、IMF7和IMF8为伪分量,包含的有效原始信号分量较少。IMF3处有一局部最大值,即出现局部最大值前的IMF1和IMF2分量包含有高频噪声。对含高频噪声分量的IMF进行小波阈值去噪后与剩余分量重构,并剔除趋势项和均值,即可得到去噪后的加速度信号。
对去噪后的加速度信号采用Simpson积分公式进行一次时域积分,从而能够得到速度信号。此时,时域积分算法将会产生误差,导致速度信号端点部分基线发生漂移。利用最小二乘法进行多项式拟合,拟合过程中发现选取多项式阶数为6时得到的速度信号效果最佳。如图7所示,速度信号中不存在明显的噪声毛刺和漂移。
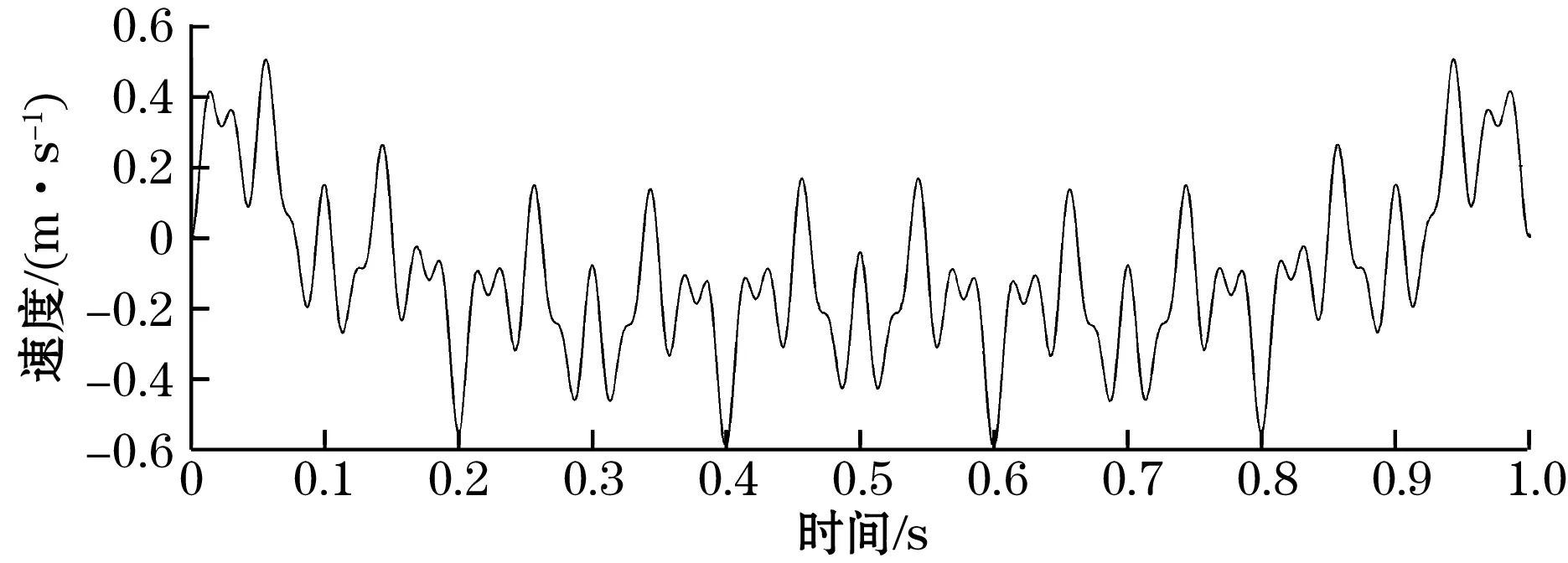
(a)时域一次积分后的速度信号
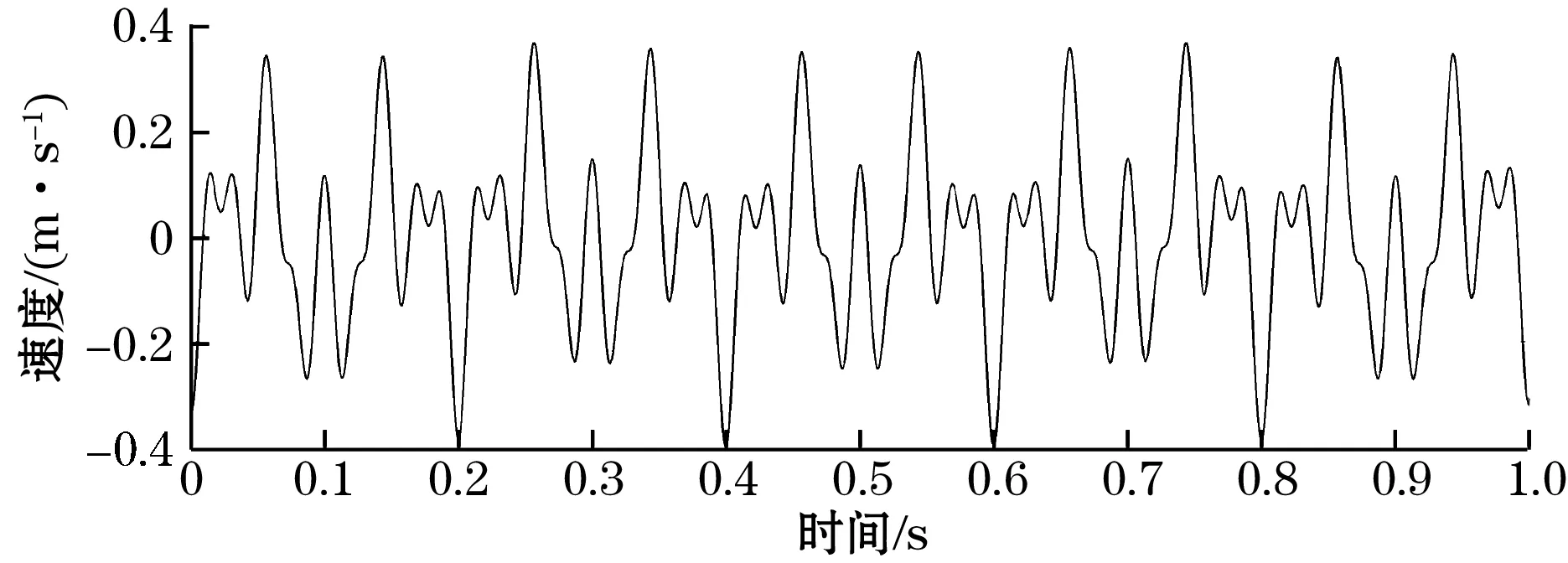
(b)多项式拟合后的速度信号图7 速度信号对比
对一次时域积分所得到速度信号,利用低频截止法进行一次频域积分后,即可得到原加速度信号所对应的位移信号。将混合积分所得到的位移信号与原位移信号进行对比,如图8所示。
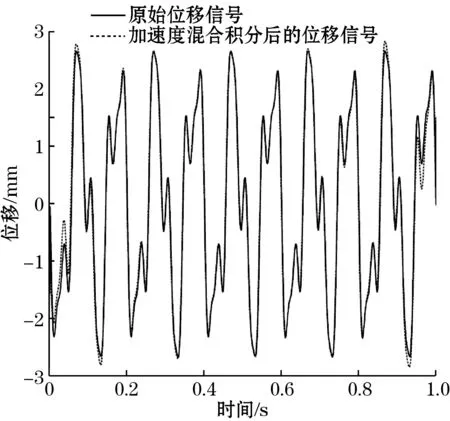
图8 混合积分前后位移信号对比
从图8可以看出,位移信号的开始部分和结束部分有一定程度的积分处理所产生的端点效应。但总体上,位移吻合度较高。采用平均绝对误差(MAE)和均方根误差(RMSE)对该混合积分算法所得到的位移信号进行评价,平均绝对误差和均方根误差越低,表明信号还原度越好。计算公式如下:
(14)
(15)
通过计算得到的平均绝对误差为0.000 114,均方根误差为0.000 159。本文设计的混合积分算法积分仿真可行,位移信号还原度高。
3.2 试验验证
本文利用搭建的卷簧振动筛试验台,通过仿真及锤击模态试验,发现其做垂直振动的模态频率为8.2 Hz。通过在振动台顶部安装电机驱动偏心质块,使偏心质块在492 r/min的转速下做圆周运动。在偏心质块离心力的作用下,不断给予振动筛激励,振动台则在垂直模态下不断在竖直方向上振动。通过安装激光位移传感器、加速度传感器以及LMS信号采集系统,实测加速度及位移信号,验证本算法。试验场地搭建如图9所示。

图9 试验现场
加速度传感器的采样点数为6 144,采样频率为1 024 Hz;位移传感器的采样点数为6 144,采样频率为1 024 Hz。所测得的加速度信号如图10所示。
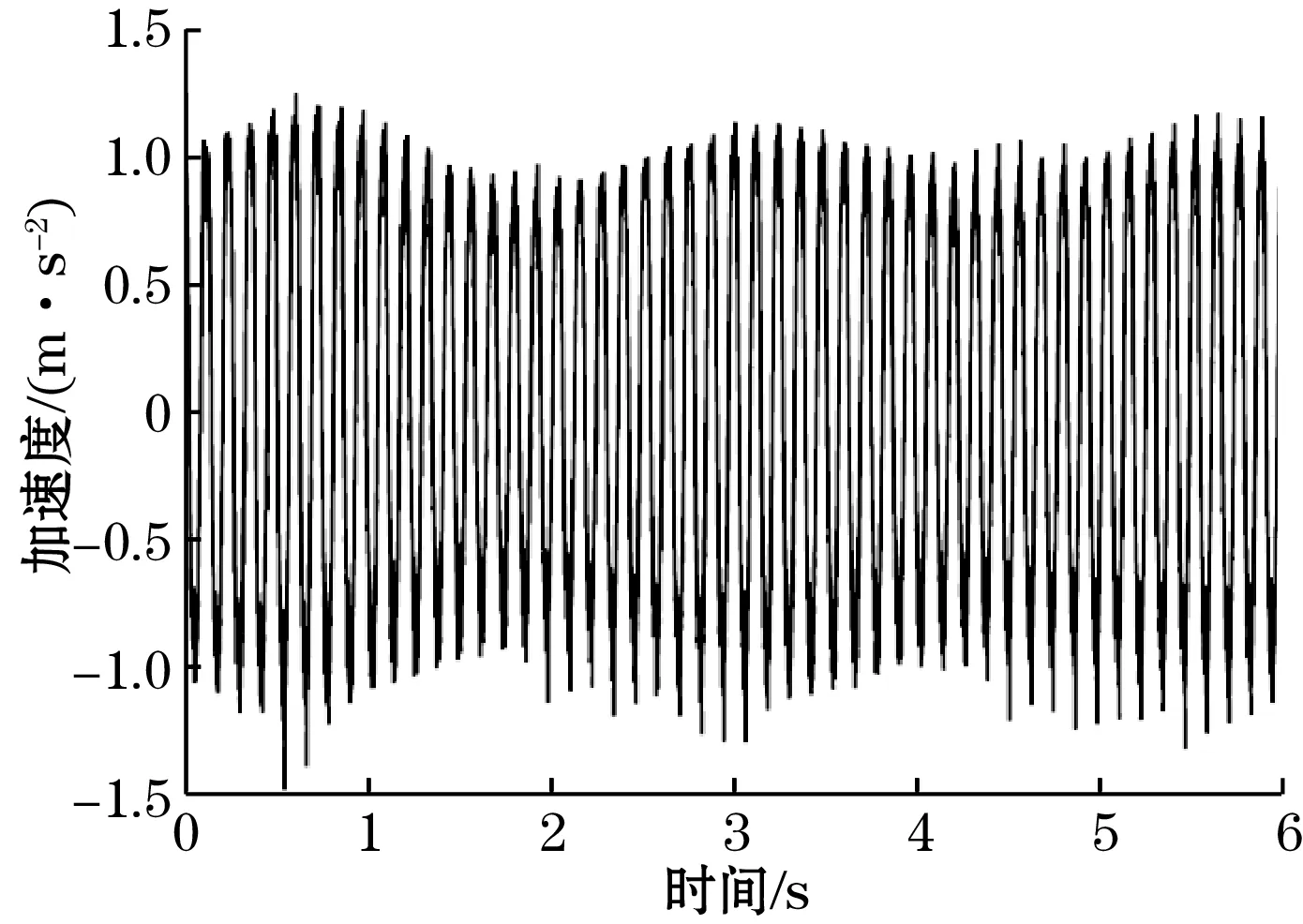
图10 加速度原始信号
对采集得到的加速度信号进行CEEMDAN分解,得到的15个IMF分量如图11所示。由图11明显看出,IMF分量包含很明显的高频噪声,IMF7分量处显现出原始信号的波形。

图11 CEEMDAN分解得到的模态分量
利用式(13),计算前14个IMF分量与加速度信号的相关系数图,如图12所示。

图12 相关系数图2
由图12可知,前5阶和后5阶IMF分量为伪分量。有效分量中第1个局部最大值拐点出现在分量IMF7处,即前6阶IMF分量是含有噪声的。
对含有噪声的IMF分量进行小波阈值去噪后与其余分量进行重构,并去除趋势项IMF15和均值,即得到预处理去噪后的加速度信号。去噪前后加速度信号的频谱对比,如图13所示,主频能量基本没有损耗。
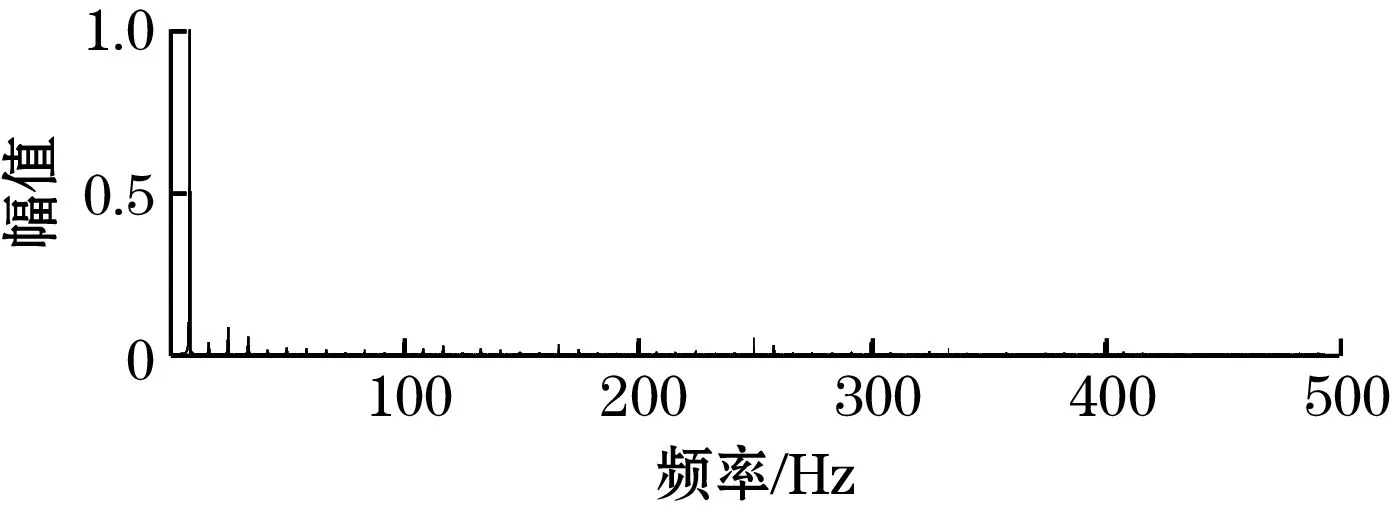
(a)原加速度信号
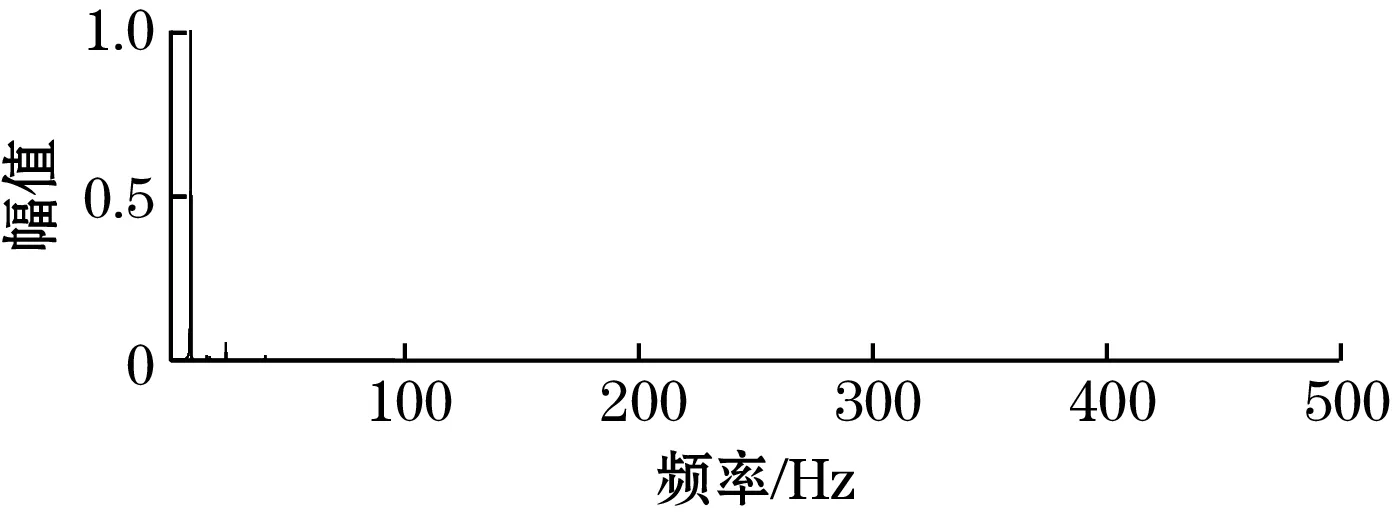
(b)去噪后的加速度信号图13 加速度信号去噪前后频谱对比
CEEMDAN和小波阈值能在一定程度上有效的剔除度加速度信号中的高低频噪声,防止后续由噪声引起的积分误差扩大。对上述去噪后的加速度信号,采用本文混合积分算法进行运算。同时,将本积分算法处理结果与EMD结合SLS时域积分算法结果和文献[15]的算法结果进行对比,利用式(14)和式(15)建立评价方式。积分后的结果如图14所示,局部放大如图15、图16所示。误差评价计算结果如表1所示。
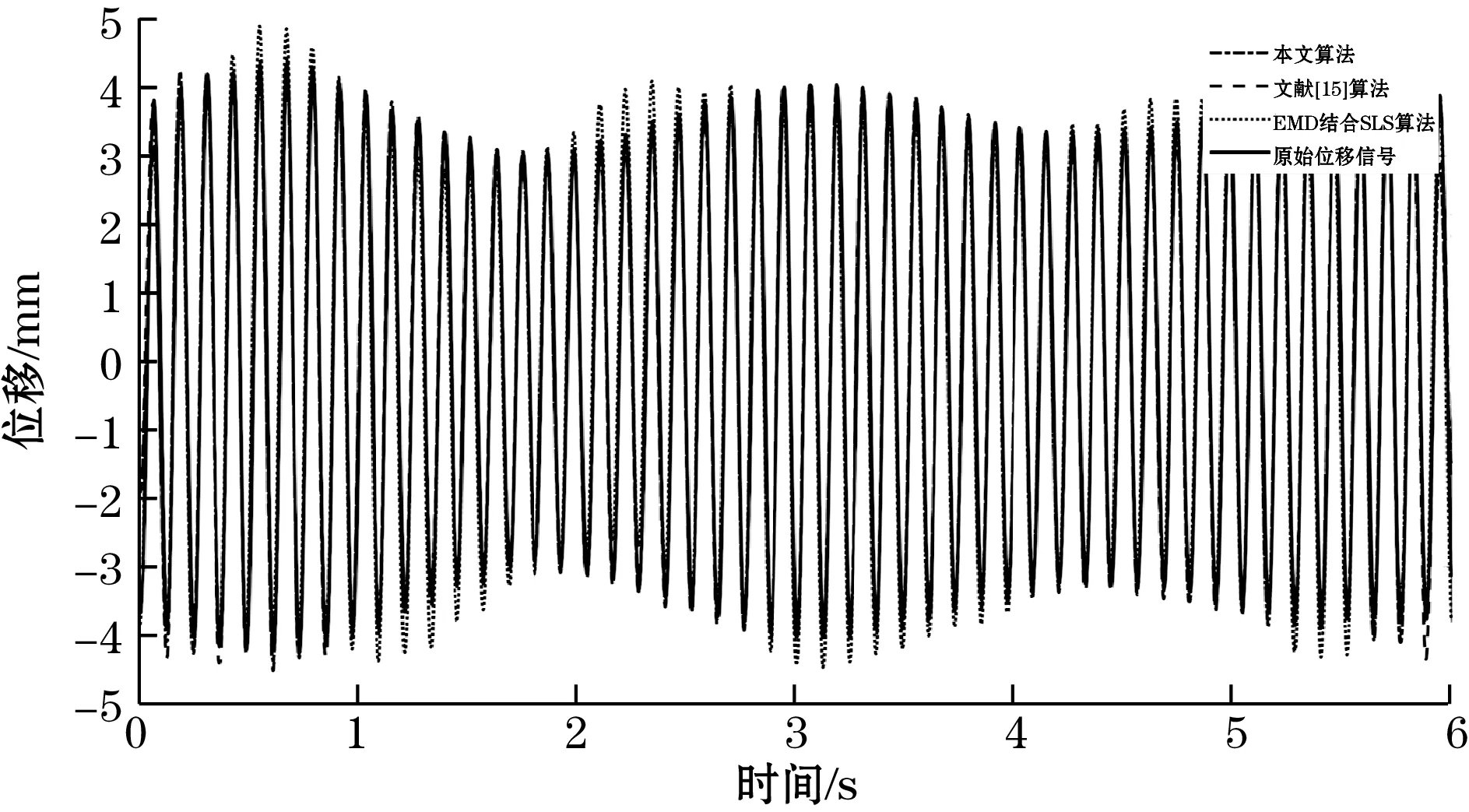
图14 积分位移算法对比
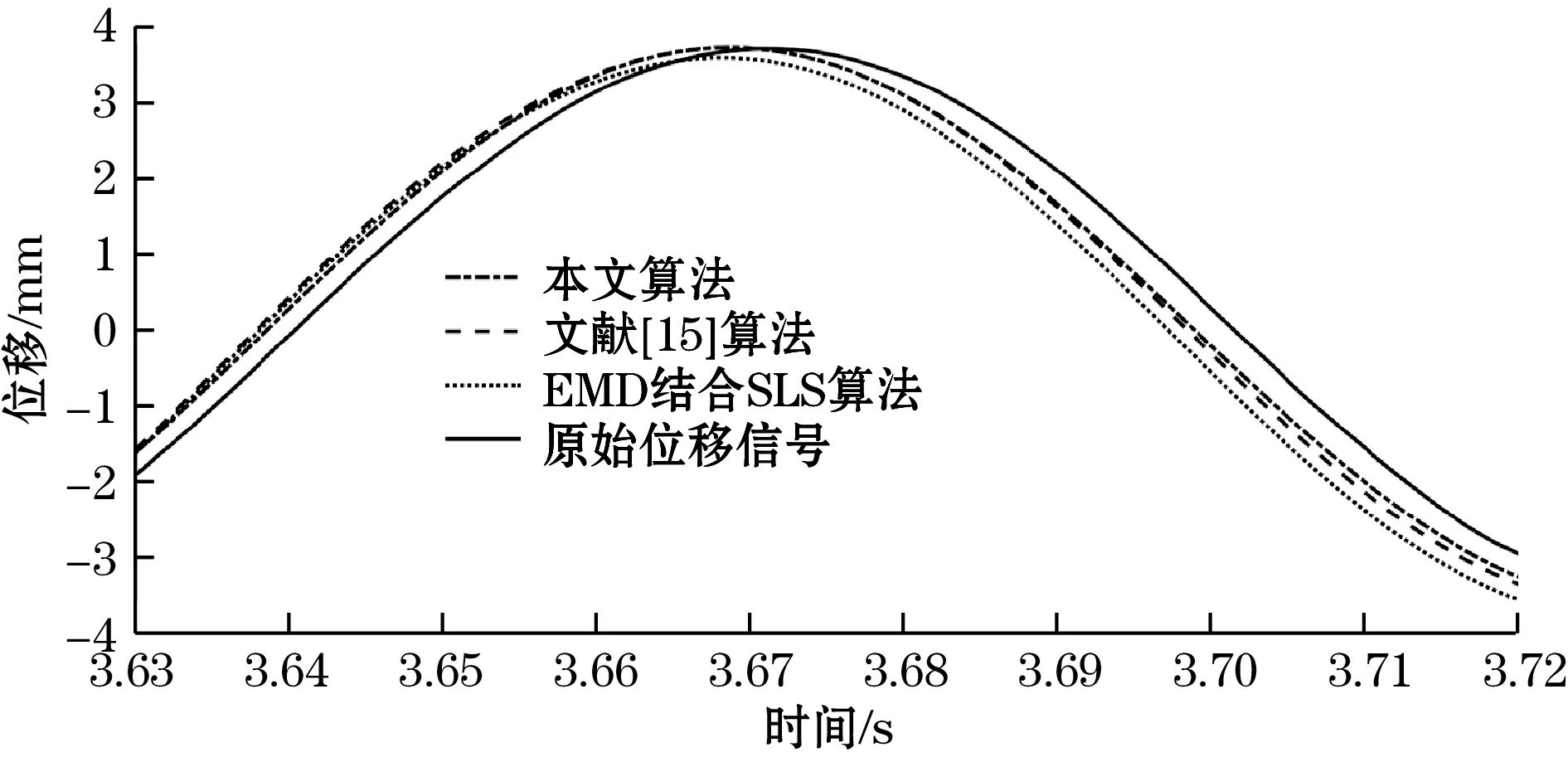
图15 局部放大图1
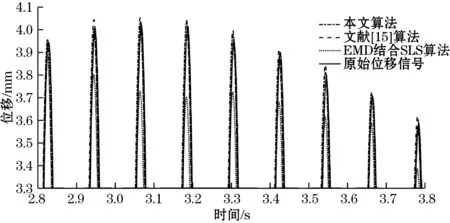
图16 局部放大图2
由图14可知,EMD结合SLS时域积分后的位移信号存在较严重的漂移误差,峰值误差较大,信号还原度最差。文献[15]的算法较两次时域积分效果好,但仍存在较高的峰值误差。本文提出的混合积分算法不存在漂移,峰值误差较小,信号拟合程度较高。
由表1可知,本文提出的基于CEEMDAN和小波阈值去噪的混合积分算法的MAE、RMSE均最小,能够在一定程度上解决位移信号漂移、误差严重的问题。
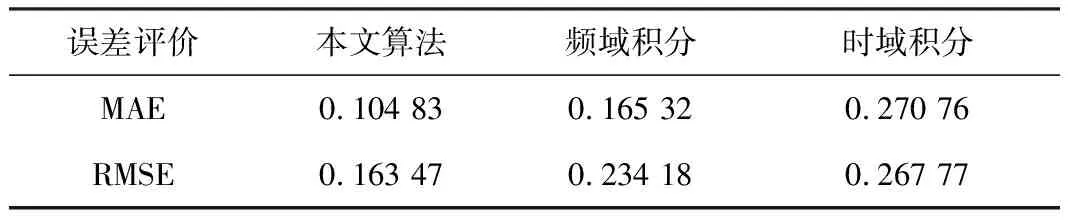
表1 误差计算结果
4 结论
设计的基于CEEMDAN和小波软阈值去噪的加速度混合积分算法,从仿真分析及试验测试结果可以看出,利用CEEMDAN算法的自适应性及模态分解的高辨识度局部特征,可以有效分辨噪声分布情况。同时,结合小波阈值去噪进行预处理的方法,能够避免采集的加速度信号中存在的高低频噪声干扰,影响积分信号的还原效果。先进行一次时域积分,避开两次时域积分造成的误差项放大现象,并与采用低频截止算法的频域积分相结合,能有效避免低频误差对积分效果的影响。但是,本文算法在计算速度及去噪范围上仍存在一定的局限性,处理的信号须具有一定长度的带宽。频域算法对于频率较低的信号处理效果不是很好,信号能量有一定损失。本文设计的混合积分算法为后续工程应用提供了参考。

