基于IIS2DH的振动信号处理与传感器设计
姜佩贺,郭 刚,吴中杰,位寅生
(1.烟台大学光电信息科学技术学院,山东烟台 264005;2.哈尔滨工业大学电子与信息工程学院,黑龙江哈尔滨 150001)
0 引言
通过分析振动信号可以提取振动源的特征,振动信号处理被广泛应用在参数检测、质量评价、状态检测和故障诊断等领域[1-3]。获取振动信号是进行信号处理的第一步,在测量机械振动时,实时加速度信号可以使用加速度传感器直接测量,而振动速度、位移以及频率的测量较困难,但更能够体现振动源的特性。例如,在汽车悬挂系统设计中,振动速度和位移用于评价减震器性能;在故障检测中,振动频率反映出故障的部位。因此,在得到加速度信号后,通过信号处理技术将加速器准确地转换为另外3种信号是进行振动分析的关键。
对于振动信号处理,周小祥[4]等提出在时域使用最小二乘法去趋势项的方法;顾明坤[5]等分析了3种加速度信号通过积分获得速度和位移信号的方法,并对3种方法进行评估;胡玉梅[6]等对加速度信号在频域内直接积分,利用积分精度控制方程保证积分精度;牟玉喆[7]等对振动信号处理算法在LabVIEW中进行实现。此外,还有部分研究者采用Wigner-Ville分布[8]、谱分析、小波分析[9]、盲源分离[10]、Hilbert-Huang变换[11]和高阶统计量分析等方法对振动信号展开分析。
总结发现,现有研究大都侧重于算法本身,算法需要借助于PC机在MATLAB或LabVIEW等大型软件中完成,而在很多场合,特别是在物联网时代,振动分析经常需要以嵌入式传感器的形式在现场实时安装、实时采集、实时处理,实时得到振动源特性。在嵌入式系统中进行振动信号处理,可以很好地解决该问题。
基于此,首先使用MATLAB评估基于去趋势项的时域分析和基于快速傅里叶变换(FFT)的频域分析两种振动信号方法;然后将两种分析方法分别在嵌入式处理器STM32F103中实现;最后搭建硬件平台,使用加速度传感器芯片IIS2DH采集加速度信号,通过嵌入式系统的算法分析获得振动的速度、位移和频率信息。
1 时域处理方法
1.1 方法概述
对加速度信号进行一次积分可得速度,对其进行二次积分可得位移。但由于噪声、零漂、非整数周期采样等原因,在积分前后要滤波和去除趋势项,具体流程如图1所示。首先,对采集到的实时加速度信号去直流和FIR滤波得到加速度信号;然后,对加速度信号一次积分后,去除一次趋势项,得到速度信号;最后,对速度信号再一次积分,去除二次趋势项后得到位移信号。
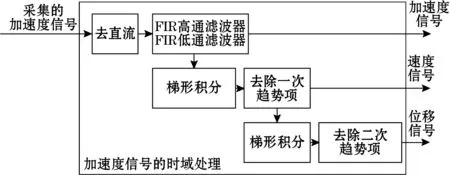
图1 时域振动信号处理流程框图
1.2 滤波与积分
采集加速度信号会混入低频和高频噪声,对噪声的积分累加将使信号发生畸变,因而需要滤除噪声。此外,在不同的应用场合,需要的振动频率范围是不同的,这也需使用滤波器滤除不需要的频率范围。采用32阶基于窗函数的FIR滤波器,并将下限和上限截止频率分别设置为1 Hz和100 Hz。虽然在相同性能条件下,FIR滤波器阶数要比IIR滤波器高,但FIR滤波器总是稳定的,且不涉及复数运算,更适合在嵌入式系统中实现。FIR滤波器用差分方程形式可以表示为
(1)
式中:x(n)和y(n)分别为输入和输出时域信号序列;bk为滤波系数。
在滤波前,需要去直流,去直流也可以看作是滤波的一部分,是将不需要的直流分量滤除。去直流的方法是求出全部N个采样点的平均值,然后每个采样点减去该值。该过程可以表示为
(2)
式中:ai为采集到的加速度信号;ai′为去直流后的加速度信号;N为采样点数;i的取值范围为0至N-1。
常见的数字积分法有梯形积分法和Simpson积分法等,梯形积分法计算简单,精度能够满足要求,适合在嵌入式系统中实现,因此采用梯形积分法。具体公式为
(3)
(4)
式中:a为加速度;v为速度;s为位移;t1为采样时间间隔,即采样频率的倒数。
1.3 去除趋势项
趋势项是由于零漂、噪声、非正周期采样等因素经积分累加后造成的信号随时间不断偏离基线的现象,趋势项影响信号的正确性,需要去除。采用最小二乘法拟合去除趋势项,具体方法为:对于速度信号,对该信号进行最小二乘法一次拟合,速度信号与拟合结果相减,即可将趋势项去除。最小二乘法一次拟合的参数为
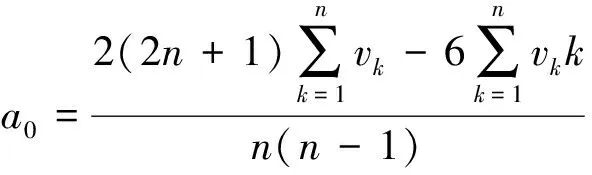
(5)
消除一次趋势项的计算公式为
(6)
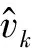
去除位移信号趋势项的方法与此类似,但由于位移信号是经过二次积分得到的,因此,需要使用最小二乘法对位移信号二次拟合,然后做差。在MATLAB中可以使用polyfit和polyval函数实现最小二乘法的参数计算与多项式拟合。
1.4 MATLAB仿真实验与结果分析
按照图1所示流程,在MATLAB中编写测试程序,假设加速度信号为a=20sin(2π×25×t),采样频率为400 Hz,经本方法得到的速度和位移信号如图2所示。
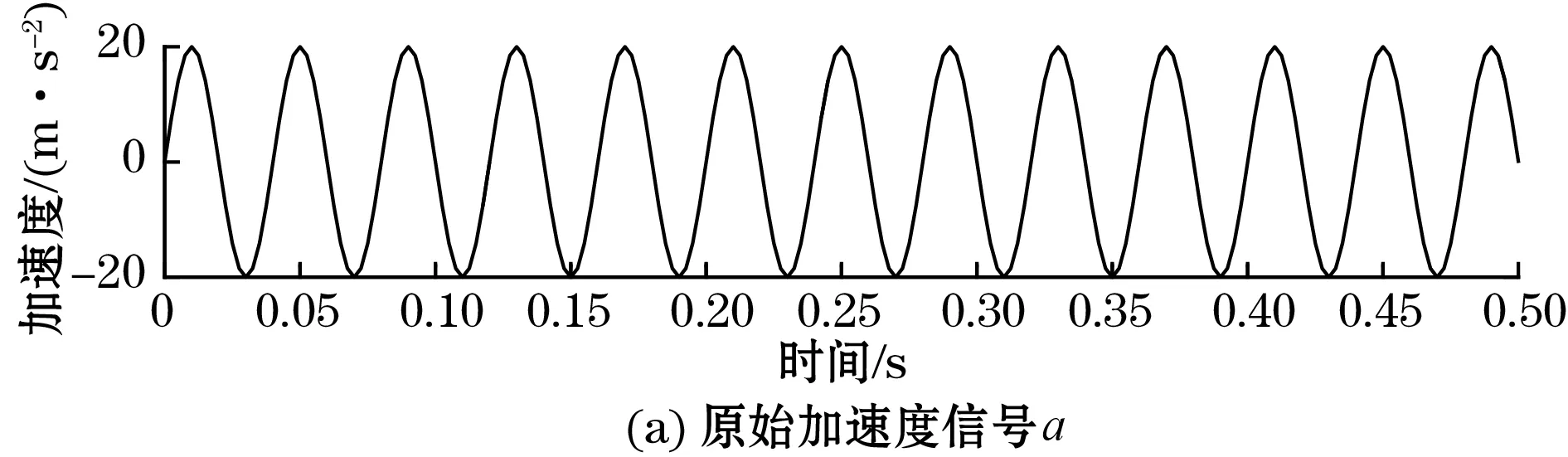
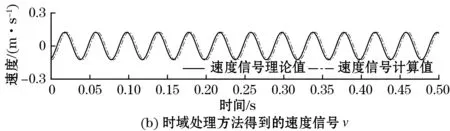

图2 时域方法对正弦加速度信号的处理结果
图2(a)~图2(c)分别为原始加速度信号a,速度信号v和位移信号s,对比发现,使用本方法可以较准确地恢复出速度信号和位移信号。分别选取理论值与计算值的极值点,经计算,速度v平均峰值误差为0.54%,位移s平均峰值误差为3.99%。由于滤波器的存在,v和s存在相移,但相移并不影响实际应用中的振动分析。
2 频域处理方法
2.1 方法概述
在频域进行振动信号处理的流程如图3所示。首先对加速度信号做FFT得到加速度频谱并进行滤波;然后,对速度频谱依次做2次频域积分,即可得到速度和位移频谱;最后,使用逆快速傅里叶变换(IFFT)得到速度和位移信号。
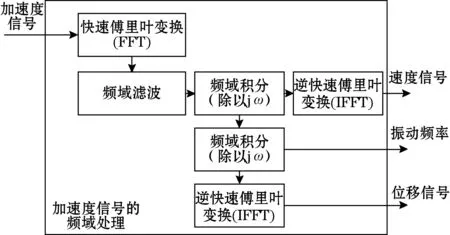
图3 频域振动信号处理流程框图
2.2 离散傅里叶变换与频域积分
时域信号经过离散傅里叶变换(DFT)可以得到频域信号,设加速度信号a(t)的频谱为X(k),则
(7)
(8)
式中N为采样点数。
设a(n)、v(n)、s(n)分别为加速度a(t)、速度v(t)和位移s(t)信号的离散化表示。每条谱线对应一个正弦波,有
ak(t)=X(k)ejωkt
(9)
则
(10)
(11)
推导得
(12)
(13)
式中:ωk=2πkΔf;Δf=Fs/n。
由上述推导可知,对加速度信号进行FFT运算后,在频域表达式上除以jω即可实现频域一次积分,得到速度的频谱,除以(jω)2即可实现频域二次积分,得到位移的频谱。
2.3 频域滤波
滤波的目的是去除噪声和非需要频率范围的振动信号。在频域,只需将低于下限截止频率和高于上限截止频率的频谱置0,即可完成滤波。与时域相同,设置下限和上限截止频率分别为1 Hz和100 Hz。
2.4 MATLAB仿真实验与结果分析
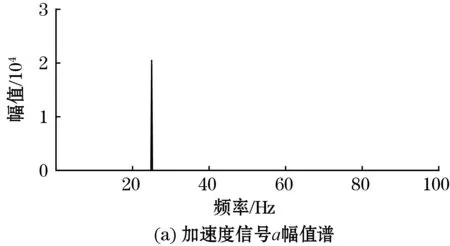
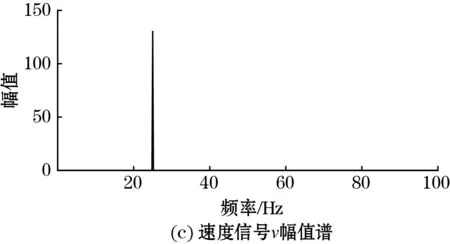
按照图3所示流程编写MATLAB程序,与时域相同,假设加速度信号为a=20sin(2π×25×t),采样频率为400 Hz,采样点数为2 048,即采样时长约为5.11 s,经本方法得到的速度和位移信号频谱,以及经IFFT变换得到的速度和位移信号如图4所示。为方便显示,图中的时域信号仅截取了0.5 s。
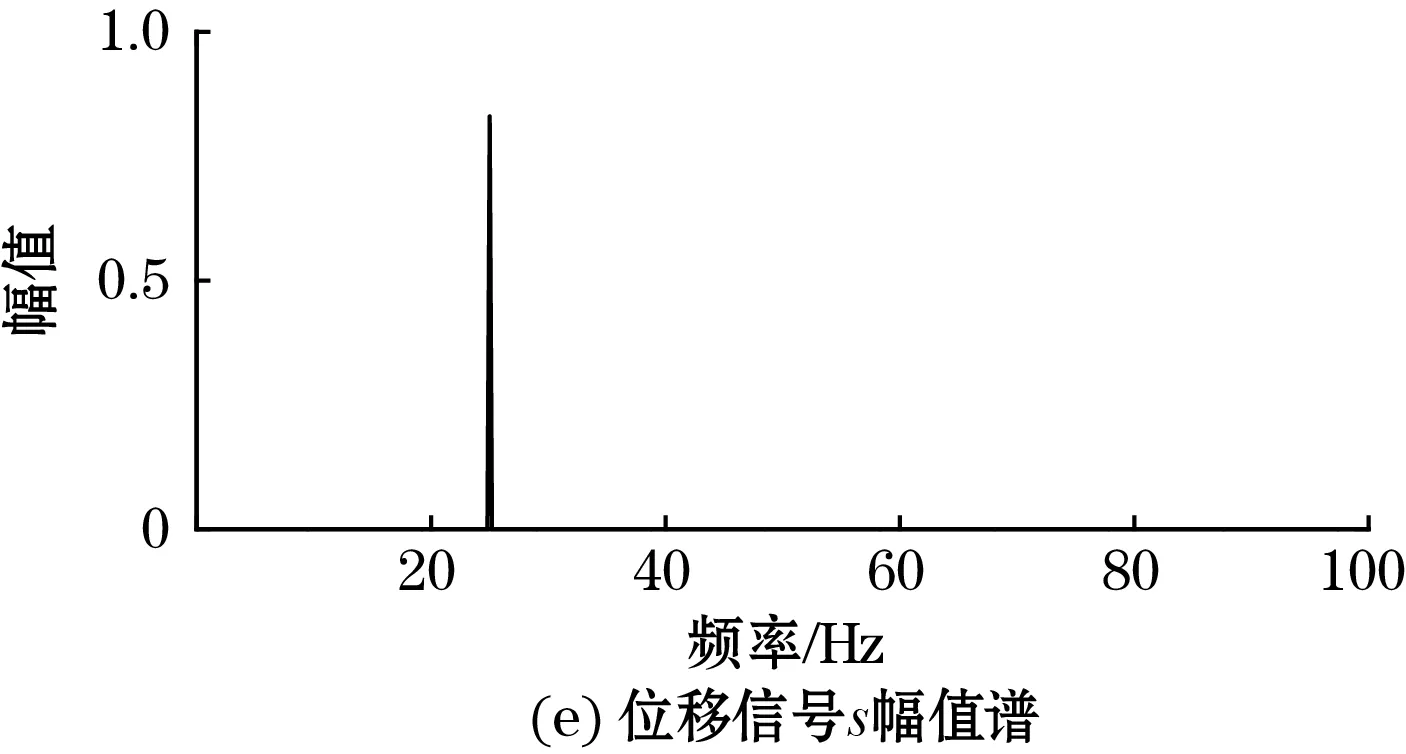
图4(b)为原始加速度a,对其做FFT后得到的幅值谱见图4(a),频域一次积分后得到速度v幅值谱见图4(c),频域二次积分后得到位移s幅值谱见图4(e),对v和s的频谱做IFFT变换,得到速度和位移信号,分别见图4(d)和图4(f)。在图4(d)和图4(f)中,理论值和计算值几乎完全重合,为便于显示,这里将虚线的理论值分别移位+0.02和+1×10-4。经计算,速度v平均峰值误差为0.39%,位移s平均峰值误差为0.79%。位移s幅值谱的极值点所对应的频率为振动频率,该频率为25 Hz,与理论值相符。
时域方法与频域方法计算结果对比如表1所示,在速度方面计算精度相差不大,但在位移方面,频域方法的计算精度显著高于时域方法,即使用频域方法可以获得更高的精度,而且计算量更小。若要进一步提高计算精度,可以增加采样点个数或修改窗函数。
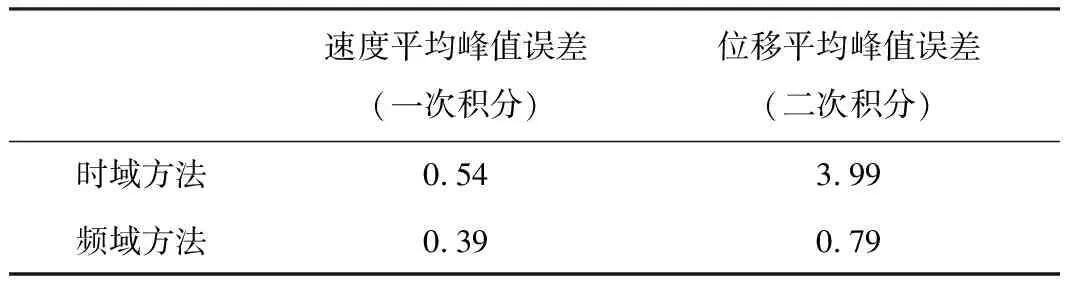
表1 时域和频域方法计算结果对比 %
3 算法在嵌入式系统中的软硬件实现及实验验证
3.1 硬件平台
硬件平台框图如图5所示,加速度传感器与嵌入式处理器共同构成振动传感器。使用加速度传感器IIS2DH实时采集加速度信号,IIS2DH是一款低功耗高性能三轴加速度传感器,量程可配置为±2g、±4g、±6g或±16g,采样频率可配置为1 Hz到5.3 kHz,对外接口为SPI和I2C。嵌入式处理器STM32F103采用Cortex-M3内核,通过SPI接口与加速度传感器IIS2DH通信,在完成信号处理后,通过串口发送处理结果。在不同的应用场合,可以通过修改硬件和软件程序采用USB、LoRa、Wi-Fi、蓝牙等不同类型的有线或无线接口发送处理结果。
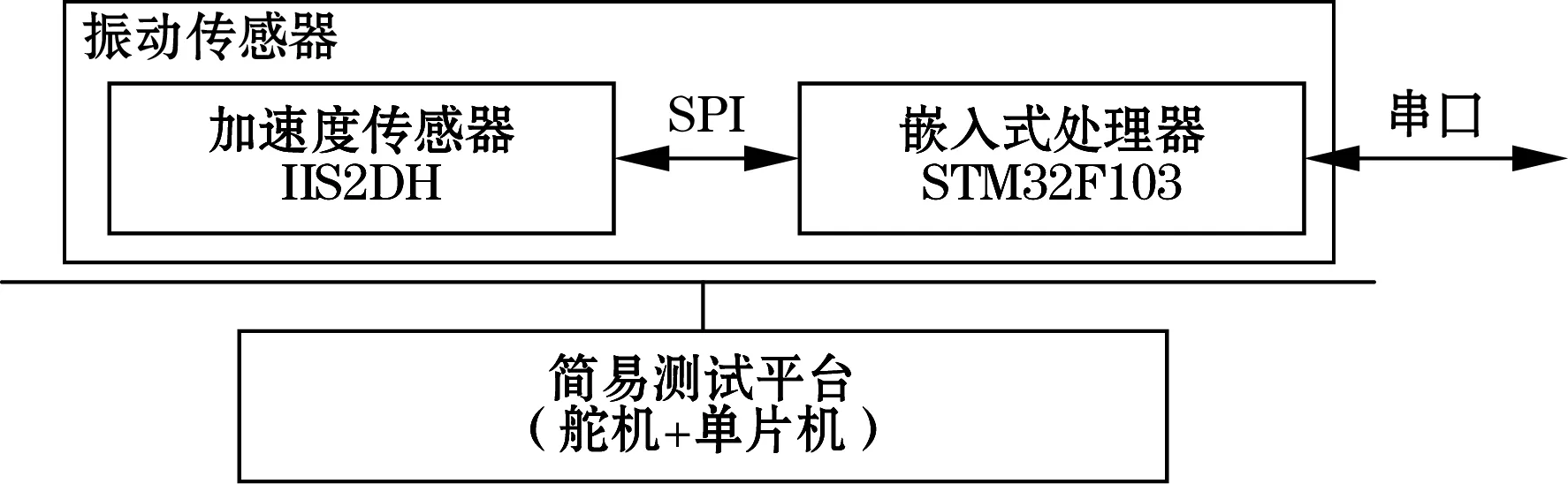
图5 振动传感器与测试平台框图
为方便测试,搭建简易测试平台,振动传感器固定在测试平台上。测试平台的“振动”由舵机产生,舵机型号为SG90,扭矩1.6 kg/cm,舵机在水平方向以圆弧形式往复运动,这样振动传感器IIS2DH即在x和y方向发生“振动”。
3.2 时域和频域方法在STM32F103中的实现
STM32F103内部不含FPU等硬件信号处理单元,所有算法需要用软件实现。通过移植DSP库,可以比较容易地实现时域和频域分析算法。
时域与频域分析的嵌入式实现流程与图1和图3相同。在时域分析算法中,滤波器的设计较关键,利用MATLAB的fdatool工具生成滤波系数,调用arm_fir_f32函数实现滤波器的设计。面向不同的上限和下限截止频率,可以生成多组参数,将参数以数组的形式保存在嵌入式处理器中,以方便在不同应用场合通过软件为系统配置不同的截止频率;在频域处理算法中,调用arm_rfft_fast_f32函数和arm_rfft_fast_f32完成FFT和IFFT运算。
3.3 实验测试与结果分析
设置振动测试平台舵机的转动角为90°,转动周期为640 ms。设置加速度传感器IIS2DH的量程为±2g,采样频率为400 Hz,设置滤波的下限和上限截止频率分别为1 Hz和100 Hz。将信号处理的全部结果通过串口发送至上位机,在实际应用中,可以根据场景需求有选择的对信号进行取舍。
时域处理结果如图6所示,图6(a)为IIS2DH采集到的加速度信号a,图6(b)为时域处理得到的速度信号v,图6(c)为时域处理得到的位移信号s,为实施对比验证,将采集到的加速度信号在MATLAB进行数据处理,安装MATLAB的PC机配置为Intel i5-3320M CPU,8GB内存,Windows 7 64 bit操作系统。图6(b)和图6(c)中,为方便显示,将MATLAB处理结果在纵向进行了平移。在处理时长方面,MATLAB进行一次数据处理的时长约为5 ms,STM32F103的处理时长约为420 ms。
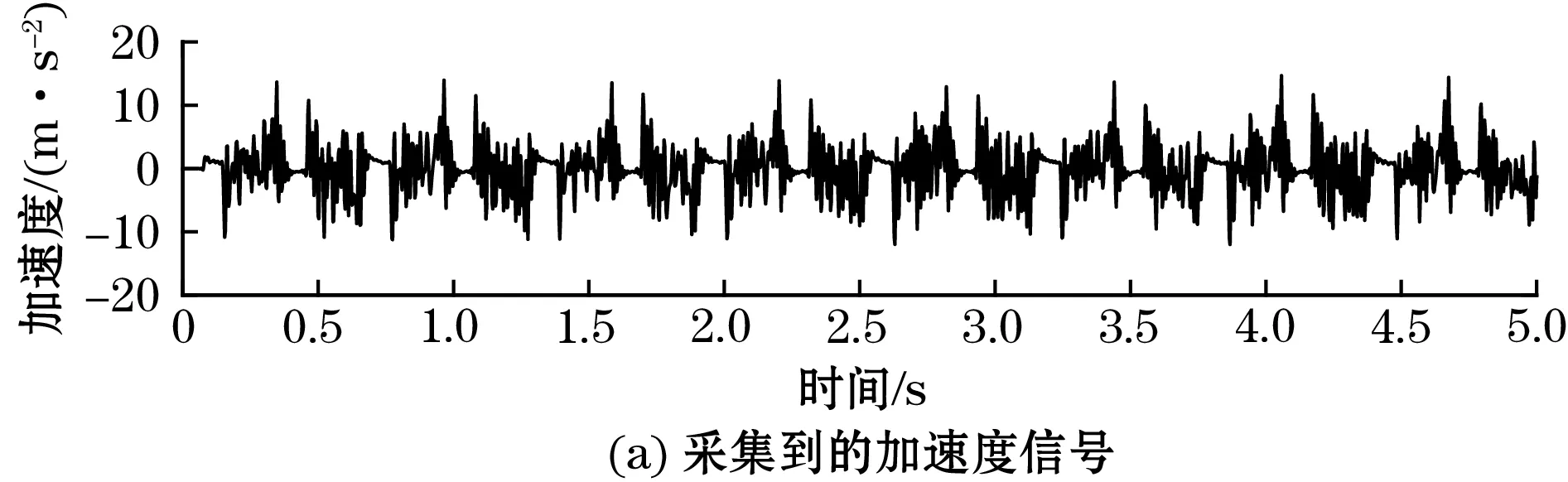
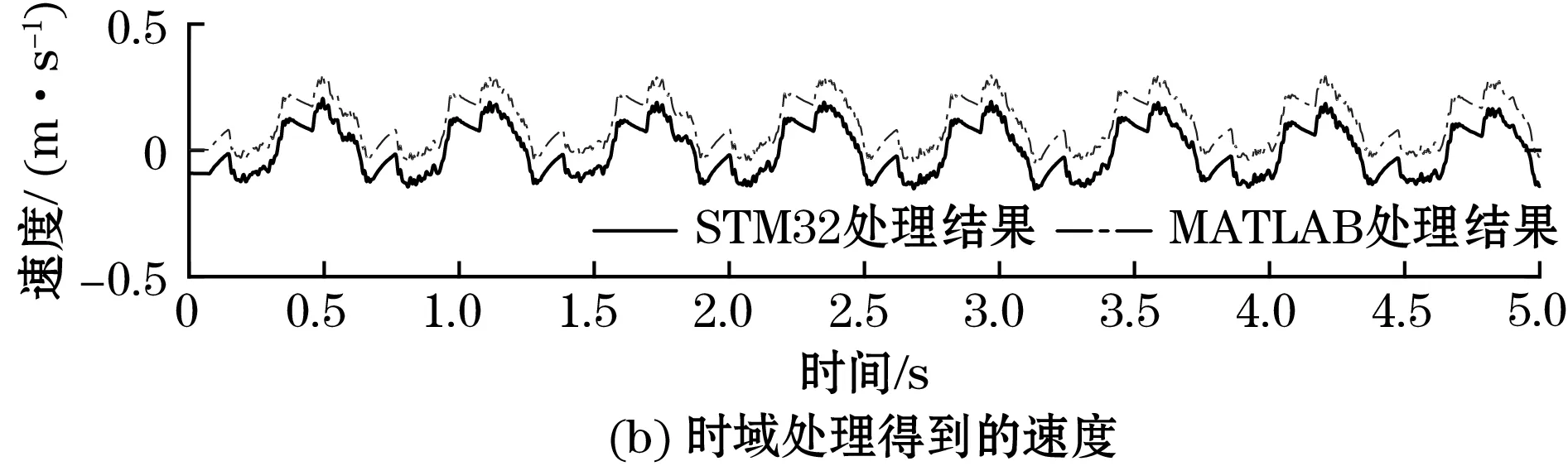
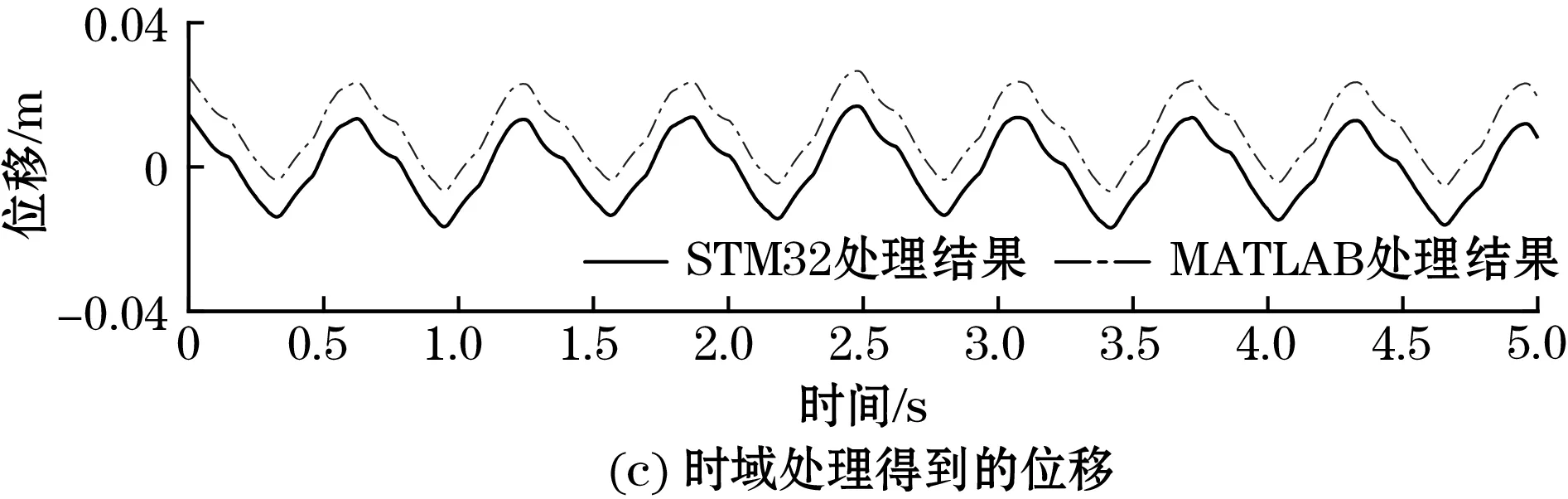
图6 STM32F103中振动加速度时域处理结果
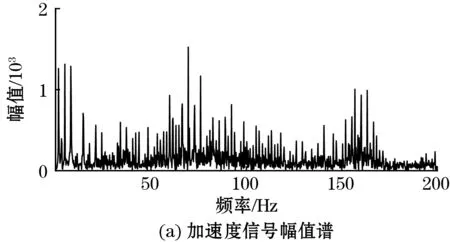
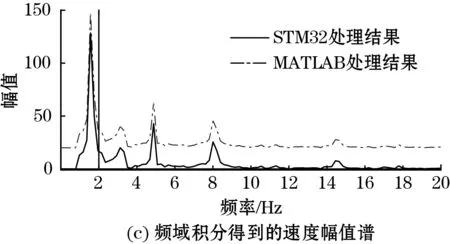
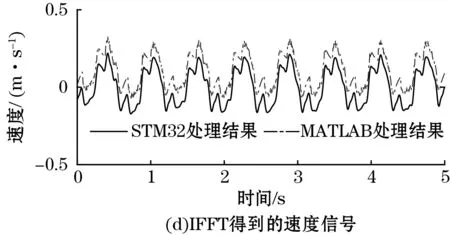
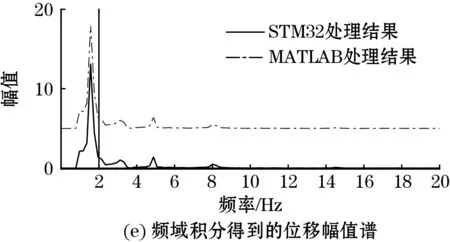
频域处理结果如图7所示,图7(b)为采集到的加速度信号,对其进行FFT变换得到的幅值谱见图7(a),在频域积分得到的速度和位移幅值谱分别如图7(c)和图7(e)所示,进行IFFT得到的速度和位移信号分别见图7(d)和图7(f),为方便显示,对MATLAB处理结果在纵向进行了平移。在处理时长方面,MATLAB进行一次数据处理的时长约0.4 ms,STM32F103的处理时长约150 ms。
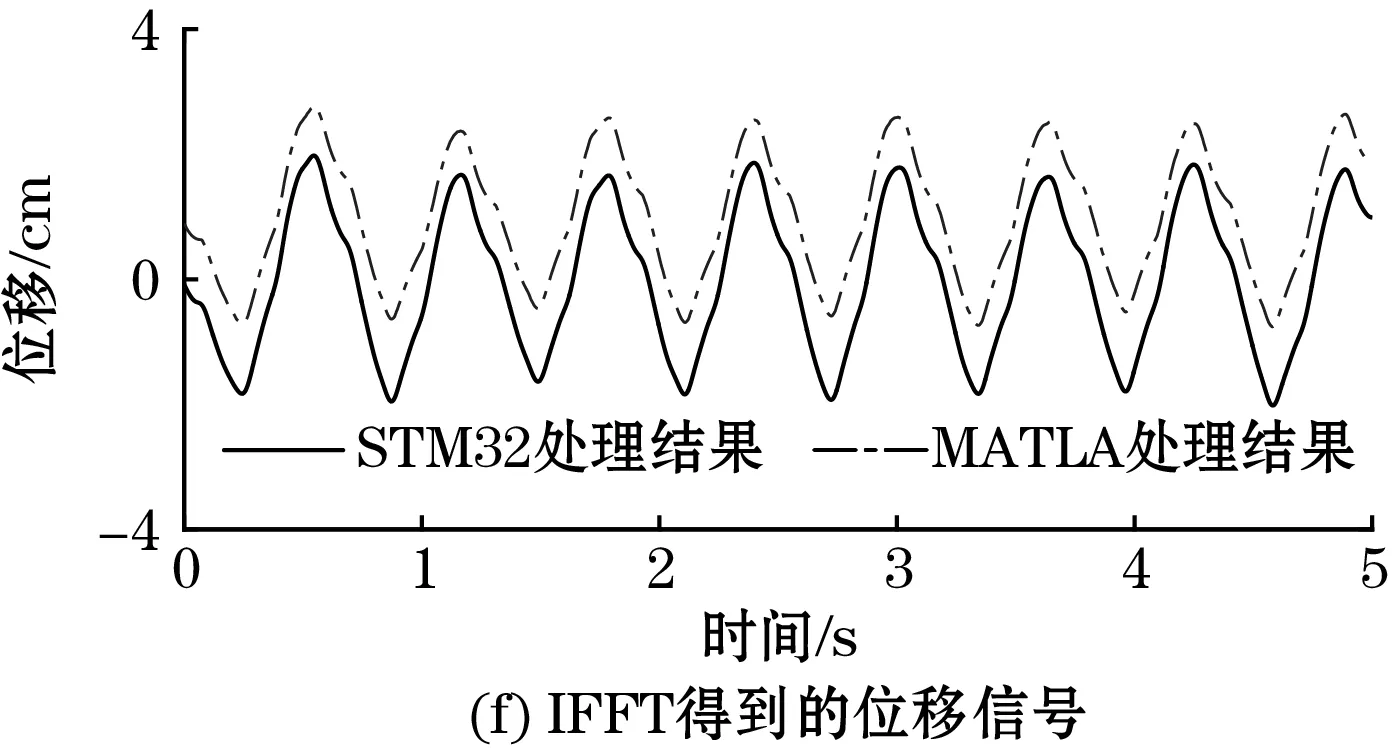
图7 STM32F103中振动加速度频域处理结果
对比STM32F103和MATLAB的处理结果可知,无论是时域还是频域,微小的差别源于串口发送时对浮点数的截断,这验证了算法在嵌入式系统中实现的正确性。嵌入式系统的数据处理能力显著低于PC机,因而算法在STM32F103的处理时长明显大于MATLAB的处理时长,但STM32F103的处理时长仍在可接受的范围内,且在实际振动分析中,通常是先采集信号再进行分析,因而对系统实时性要求不高。

4 结论
小型化、现场化和实时化是振动分析系统的发展方向。本研究采用加速度传感器IIS2DH采集加速度信号,在STM32F103中分别实现了基于去趋势项的时域分析方法和基于IFFT的频域分析方法。测试结果表明嵌入式中振动分析结果与MATLAB计算结果吻合,算法实现正确。利用所提出的方法可以将振动分析系统以传感器的形式安装在测试现场,实现实时安装、实时采集、实时处理、实时得到振动源特性。

