用于Nested阵列的多测量矢量DOA估计算法

王 璐，陶海红，李 靖，裴 悦，智开宇

(1.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

波达方向 (Direction of Arrival，DOA) 估计是阵列信号处理领域的热门方向之一[1]，其基本问题是确定同时处在空间某一区域内多个感兴趣的信号到达阵列参考阵元的方向角[2]。对于传统均匀排布的阵元，采用子空间类[3]算法测向其自由度(Degree of Freedom，DOF)是有限的。对于阵元个数为N的均匀线性阵列(Uniform Linear Arrays，ULAs)，用传统的子空间类算法测向其DOF为N-1，即DOF受到阵列孔径的限制[4]。针对此情况，文献[5]提出嵌套阵列，即Nested阵列，大大增加了自由度。

由于压缩感知[6-7]技术可以突破Nyquist采样定理的限制，仅通过少量快拍便可恢复出原始信号[8]，将压缩感知技术引入DOA估计是大势所趋[9-13]。文献[14]提出正交匹配追踪算法，文献[15]提出基于奇异值分解的1范数重构(1Reconstruction after Singular Value Decomposition，L1-SVD)算法等。但是，匹配追踪类算法的超分辨能力稍弱，1范数的稀疏约束能力大于MP算法，且基于1范数类方法在低信噪比、小快拍的现代复杂电磁信号环境中也能适应。

Nested阵列利用Khatri-Rao积操作[4]将协方差矩阵向量化后,可认为是单测量矢量(Single Measurement Vector，SMV)模型，传统追踪算法和正交匹配追踪算法在该SMV模型下估计多个信源精度不高，由此本文在空间平滑算法[16]的基础上提出了一种用于Nested阵列的多测量矢量(Multiple Measurement Vector，MMV)DOA估计算法，将SMV模型转为MMV模型并采用L1-SVD算法完成DOA估计，最后实验仿真分析比较3种算法在信源数多于物理阵元个数的情况下的测向性能。首先介绍了Nested阵列的信号模型，然后分别给出基于SMV模型和MMV模型的二级嵌套阵的稀疏表示，仿真比较了基于SMV模型稀疏表示的基追踪算法和正交匹配追踪算法以及所提算法的测向性能和均方根误差，证明了在Nested阵列下所提算法相比于其他算法的优势。

1 Nested阵列的信号模型

1.1 Nested阵列

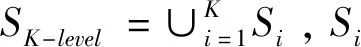
(1)

K级嵌套阵下第i级示意如图1所示。

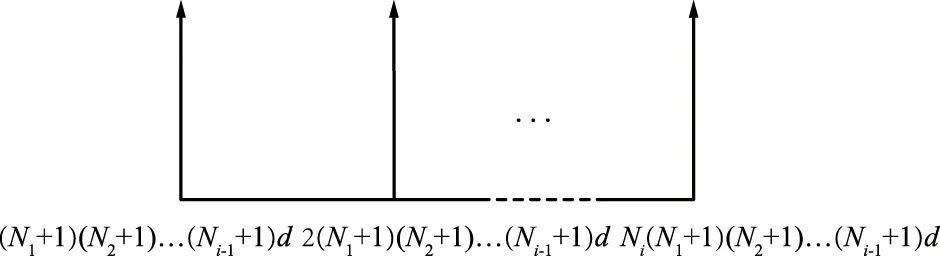
图1 K级嵌套阵下第i级示意Fig.1 Schematic diagram of level i under K-level nested array

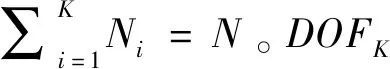
(2)

当嵌套级数大于2时，得到的差协同阵列将不再连续，即阵列间距不再连续，出现孔。故考虑二级嵌套阵的模型。

假设二级嵌套阵列总阵元数为N，第一级间距为d，阵元个数设置为N1，第二层间距为(N1+1)d，阵元个数为N2，则有N=N1+N2。二级嵌套阵物理阵列的阵元位置为：

S2={n1d,n2(N1+1)d},n1=1,2,…,N1,n2=1,2,…,N2。

(3)

通过Khatri-Rao积，二级嵌套阵列可以生成N2个阵元，其中不冗余的虚拟阵元个数为(N2-2)/2+N，间隔为d。N1=N2=3的二级嵌套阵列的阵元位置排布如图2所示，通过Khatri-Rao积后形成的虚拟阵列及每个阵元出现次数如图3所示。

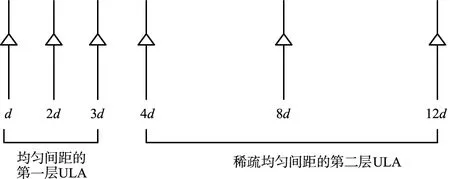
图2 物理阵元排布Fig.2 Physical array element arrangement

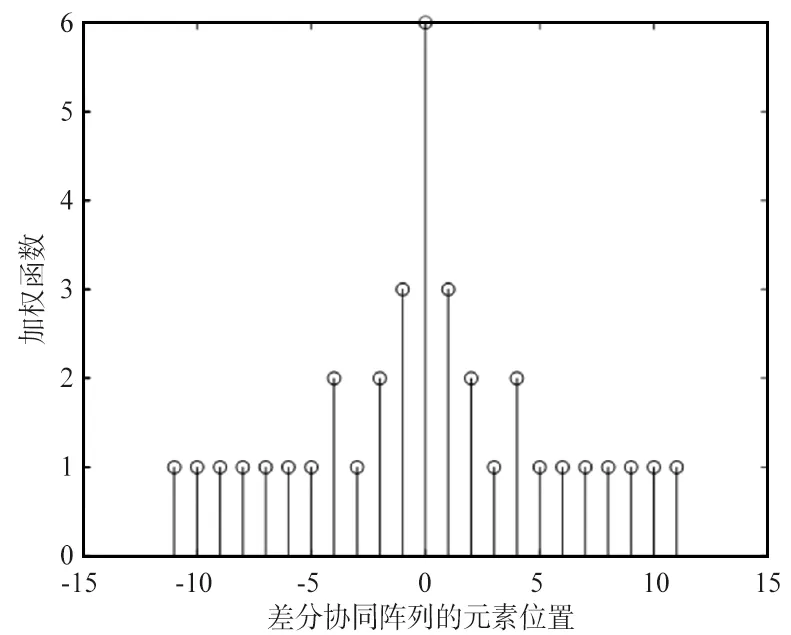
图3 二级嵌套阵的加权函数Fig.3 Weighting function of two-level nested array

1.2 阵列模型

假设有D个远场窄带信号源以角度θi(i≤D)入射到N个阵元组成的线阵上，接收信号可表示为：

x[k]=As[k]+n[k]，

(4)

式中，A=[a(θ1)a(θ2)…a(θD)]为阵列流形矩阵，a(θi)为N×1维，为θi角度对应的导向矢量，第i个阵元的值为exp(j2πdisinθ/λ)；s[k]=[s1[k],s2[k],…,sD[k]]T表示源信号矢量，k=1,2,…,Ksnap,称为快拍数，Ksnap表示阵元接收数据的总快拍数。

假设信号独立且噪声为加性高斯白噪声。则有：

(5)

将Rxx向量化，可得：

(6)

2 基于MMV模型的L1-SVD算法

2.1 SMV向MMV模型转化方法研究

在构造多快拍数据时，有2个基本要素需要注意：

(1) 转换后的多快拍数据应该含有转换前单快拍数据的所有信息，可以冗余但是尽量不要缺失。

(2) 因为多快拍数据是由同一组阵元上多次采样得到的，导致多快拍数据的阵列流形是一致的。相对应的，在构造多快拍矩阵时也要注意多个快拍数据之间物理结构相同或者近似，方便之后选取测量矩阵。

针对这2点要素，可以开始阵元的选取。阵元的选取可以采用间隔选取或者平移选取等方式，只要各个快拍的阵元个数和位置都符合(2)的要求。借鉴空间平滑[16]的思想，将虚拟阵列接收数据划分为重叠子阵，每个子阵数据看作一个快拍，构成新的接收数据矩阵的一列，但是这样做是建立在规则阵列的基础上的。与空间平滑算法目的是为解决协方差矩阵不满秩不同的是，构建重叠子阵的目的更多是为了尽可能准确地构造多快拍的数据。首先，对式(6)的接收数据进行去冗余重排的处理，得到的阵列模型[4]为：

(7)

得到虚拟阵元数据后，可以将数据进行不重叠划分或者重叠划分子阵2种操作。2种操作理论上都是可行的，但是为了保证每个快拍的阵元之间的相位中心尽量近，避免模糊的同时又不丢失原虚拟接收阵列的信息，考虑重叠子阵的划分方式。子阵之间尽可能重叠，即每次只向右滑一位直至最后一个阵元。阵元平滑示意如图4所示。

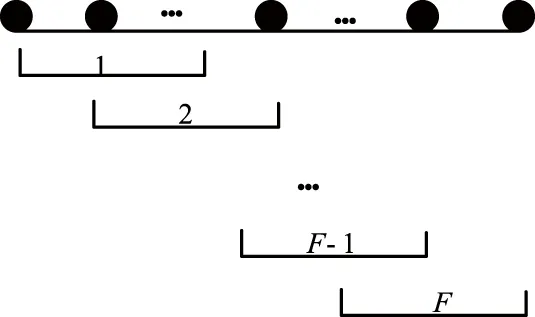
图4 阵元平滑示意Fig.4 Schematic diagram of array element smoothing

已经确定好了平滑方式，下一步确定每一个子阵的阵元个数Q和构造的快拍数F。每个子阵阵元个数过少会影响阵列自由度，而快拍数在很多时候又会影响算法精度。在实际应用中，设计模型的快拍数和每个子阵的阵元个数可根据需要做调整。

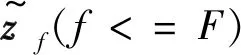
(8)

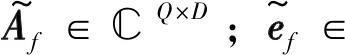
(9)

(10)

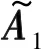
(11)

式(9)中，Φ=diag(e-j(2π/λ)dsin θ1,e-j(2π/λ)dsin θ2,…,e-j(2π/λ)dsin θD)。Φf-1即是对Φ求f-1次幂。

(12)

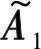
(13)

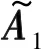
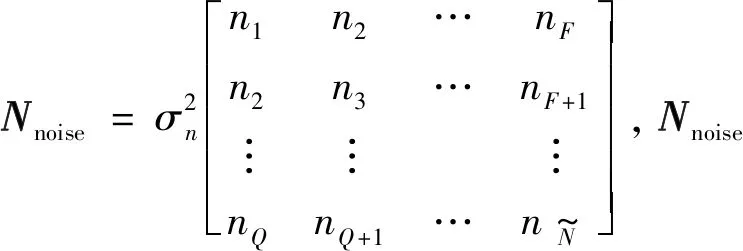
至此，得到构造的多快拍数据模型。接下来，将应用MMV模型的经典压缩感知算法——L1-SVD算法来完成DOA估计。

2.2 Nested阵列下基于MMV模型的L1-SVD算法

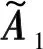
Y=AobsS+Nnoise。

(14)

为了解决S在行项不存在稀疏性的问题，对S的每一行进行二范数处理，得到的结果为：

(15)

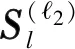
(16)

利用文献[15]方法求解式(16)。二级嵌套阵下基于矩阵奇异值分解的1范数重构算法步骤如下：

步骤1：得到Ksnap次有限快拍下的物理阵列接收数据，x(k),k=1,2,…,Ksnap；

步骤2：求x(k)的采样协方差矩阵Rxx；

步骤3：将Rxx向量化，得到z；

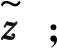
步骤6：按照式(13)构建稀疏字典Aobs；

步骤7：将Y按照文献[15]进行矩阵奇异值分解；

步骤8：按照文献[15]所示方法，利用CVX工具箱求解式(16)，所求结果行最大值对应角度即为所求角。

3 实验仿真及性能分析

将式(7)模型稀疏化，令L为空间栅格个数，对p填充零元素，得到SMV模型为：

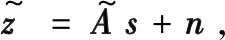
(17)

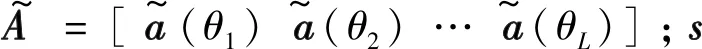
通过几组仿真实验验证3种算法性能。比较在式(17)下采用文献[13]的OMP算法、采用CVX工具箱求解的基追踪算法、所提MMV模型下的L1-SVD算法3种算法的性能。定义均方根误差(Root Mean Square Error，RMSE)为：

(18)

式中，D为信源个数；Mc表示蒙特卡罗试验次数。

仿真实验一：设置9个窄带远场非相干点频信号源，分别以-60°，-45°，-30°，-15°，0°，15°，30°，45°，60°入射到阵面。信噪比均为10 dB，频率分别为2.2，2.3，1.8，1.5，2.6，2.9，1.9，3.6，3.1 MHz，网格划分间隔为0.5°，快拍数取1 024。噪声假设为功率为1 W的高斯白噪声。验证信源个数多于物理阵元数目时算法估计性能，N=6时3种算法DOA估计结果如图5所示。图5中估计角度数值如表1所示。

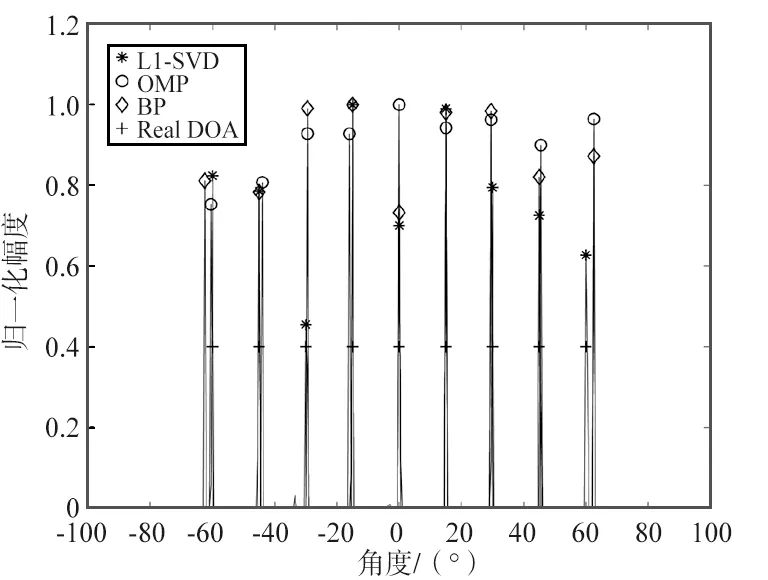
图5 N=6时3种算法DOA估计结果Fig.5 DOA estimation results of the three algorithms when N=6

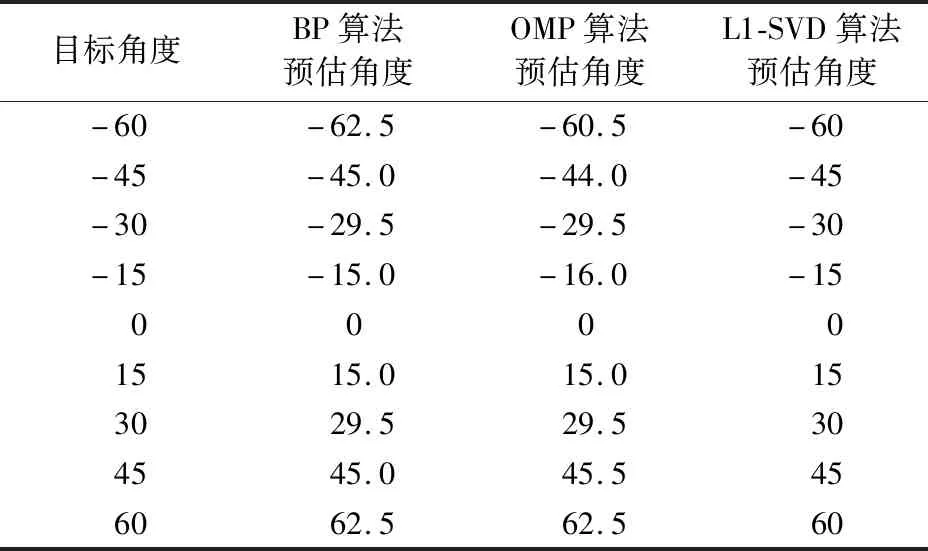
表1 信源个数多于物理阵元时3种算法角度估计Tab.1 Angle estimation of three algorithms when the number of signal sources is more than that of physical array elements 单位：(°)

对比图5和表1，当估计信源为9时，在上述仿真条件下，3种算法能够对9个角度进行分辨，但是BP算法和OMP算法均存在误差，而L1-SVD算法可以实现精确测向。统计3种算法在9个信号源下的均方误差，OMP算法均方误差约为1.013 8°,而BP算法均方误差约为1.201 8°，L1-SVD算法均方误差为0°。相较而言，在上述仿真条件下，3种算法测量精度排序为L1-SVD算法>OMP算法>BP算法。从信源估计个数分析，在同一仿真条件下所提算法对多个信源和单个信源均能实现准确估计，性能好于OMP算法和BP算法。

实验仿真二：设置2个远场窄带点频非相干信号源，入射角度分别为-5°，5°，频率分别为1.3，2.4 MHz，快拍数为1 024，网格划分间隔为0.5°。噪声为功率为1 W的高斯白噪声，信噪比变化范围为-14∶1∶20。每个信噪比下进行500次蒙特卡罗实验，3种算法RMSE随信噪比变化如图6所示。

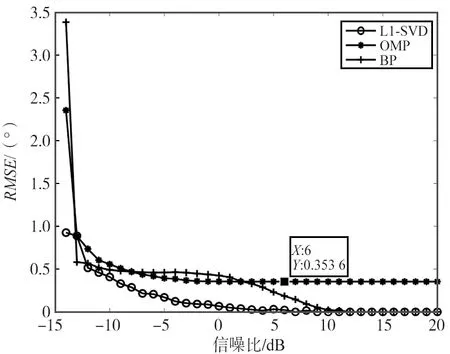
图6 3种算法RMSE随信噪比变化Fig.6 Variation of RMSE of the three algorithms with the signal-to-noise ratio

由图6可以看出，3种算法的曲线均呈现随信噪比增加测向估计的RMSE降低的趋势。其中，OMP算法在6 dB趋于稳定，角度测向误差趋于0.353 6°；BP算法在10 dB趋于稳定，角度测向误差趋于0；L1-SVD算法在0 dB趋于稳定，且角度测向误差趋于0。在上述条件下基于MMV模型的L1-SVD算法优于BP算法和OMP算法，其中OMP算法在性能稳定时还有0.353 6°误差，性能为三者中最差。

考虑到上述仿真条件的SMV模型是Nested阵列对x(k)求取协方差矩阵向量化后去除冗余和重排得到，该模型噪声将不再是高斯白噪声且阵列数据可近似认为单快拍的相干数据，考虑到算法本身的因素，故SMV模型下2种算法测向精度不高。所提算法首先利用空间平滑算法，构造多快拍数据的同时对相干数据源做了处理，同时利用矩阵奇异值分解降低了单快拍转为多快拍数据后的运算复杂度并削弱了部分噪声，且考虑L1-SVD算法本身性能的因素，故性能相较于SMV模型下的BP算法和OMP算法得到提升。

实验仿真三：设置2个窄带远场非相干点频信号源，入射角度分别为-5°，5°，频率分别为1.3，2.4 MHz，网格划分间隔为0.5°，2个信源信噪比均为10 dB，噪声为功率为1 W的高斯白噪声。快拍数5∶50∶1 000变化。每个快拍数下进行500次蒙特卡罗实验。3种算法RMSE随快拍数变化如图7所示。

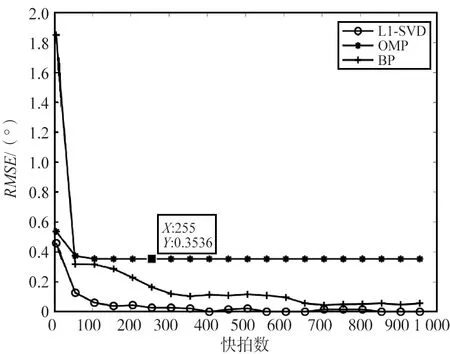
图7 3种算法RMSE随快拍数变化Fig.7 Variation of RMSE of the three algorithms with the number of snapshots

由图7可以看出，3种算法的曲线均呈现随快怕数增加测向估计的RMSE降低的趋势。其中，OMP算法在快拍数为255时趋于稳定，角度测向RMSE趋于0.353 6°；BP算法快拍数从605开始角度测向RMSE在0值附近震荡；L1-SVD算法快拍数从155开始角度测向RMSE在0值附近震动。在上述条件下所提算法优于基于SMV模型的BP算法和OMP算法，其中OMP算法在性能稳定时还有0.353 6°误差，性能为三者中最差。

实验仿真四：设置7个窄带远场非相干点频信号源，入射角度分别为-43°，-28°，-14°，0°，18.5°，32°，44.5°，频率分别为2.2，2.3，1.8，1.5，2.6，2.9，1.9 MHz，网格划分间隔为0.5°，7个信源信噪比均为10 dB，噪声为功率为1 W的高斯白噪声。快拍数50∶100∶2 000变化。每个快拍数下进行500次蒙特卡罗实验。2种算法RMSE随快拍数变化如图8所示。

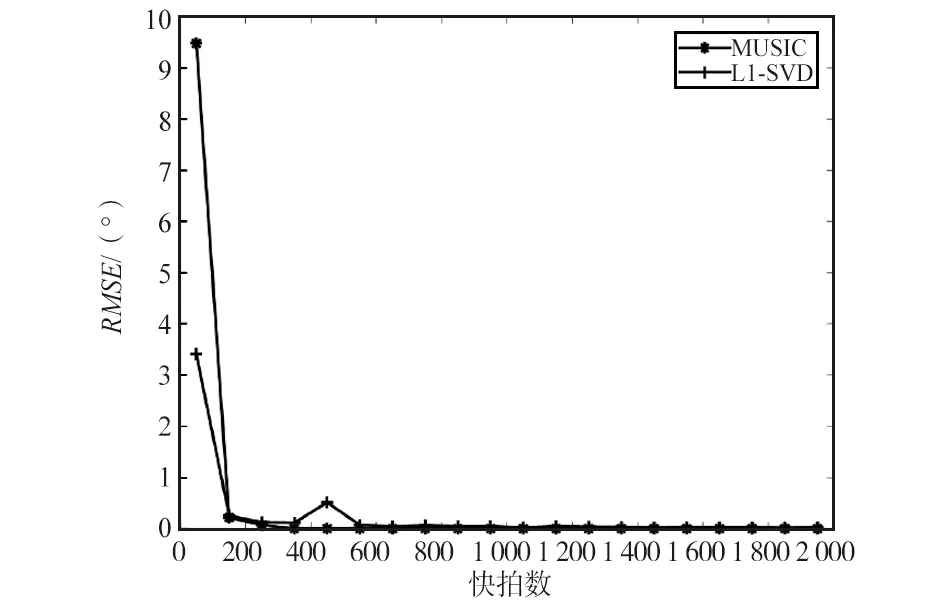
图8 2种算法RMSE随快拍数变化Fig.8 Variation of RMSE of the two algorithms with the number of snapshots

实验仿真五：设置7个窄带远场非相干点频信号源，入射角度分别为-43°，-28°，-14°，0°，18.5°，32°，44.5° ，频率分别为2.2，2.3，1.8，1.5，2.6，2.9，1.9 MHz，网格划分间隔为0.5°，快拍数取512，噪声为功率为1 W的高斯白噪声。信噪比-10∶2∶10变化。每个快拍数下进行500次蒙特卡罗实验。2种算法RMSE随信噪比变化如图9所示。

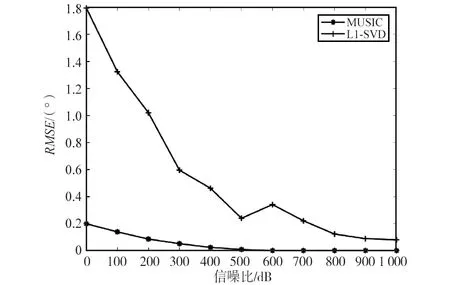
图9 2种算法RMSE随信噪比变化Fig.9 Variation of RMSE of the two algorithms with the signal-to-noise ratio

MUSIC算法的复杂度体现在协方差矩阵的子空间分解，复杂度约为O(Q3) ，L1-SVD算法的复杂度约为O(D×L)3，复杂度高于MUSIC算法。但对比实验仿真四和实验仿真五可发现,在快拍数较低如快拍数为50的情况下，L1-SVD算法的误差约为3.412°，而MUSIC算法的误差约为9.481°，证明低快拍数下L1-SVD算法性能好于MUSIC算法，但低信噪比的情况下，从图9可知,L1-SVD算法性能弱于MUSIC算法。

4 结束语

本文从压缩感知求解欠定问题的角度出发，将嵌套阵模型稀疏化，并用压缩感知的经典算法求解。本文比较了嵌套阵下基于SMV模型的BP算法、OMP算法和基于MMV模型的L1-SVD算法估计多个信号源角度情况，仿真表明，基于MMV模型的L1-SVD算法可准确估计信源个数多于物理阵元个数的目标信号的角度，且分辨率优于其他2种算法。同时，从3种算法的信噪比和快拍数的RMSE曲线分析可知，基于MMV模型的L1-SVD算法性能优于其他2种算法，且在小快拍数下估计多个信号源方向时，角度估计性能优于MUSIC算法。本文方法完全可以扩展到二维Nested阵列，能够实现对二维角度的估计。