温度和晶粒尺寸及分布影响下的氧化铝纤维烧结晶粒长大的相场模拟
张鲁,刘陆群,唐赛,马运柱,刘文胜
温度和晶粒尺寸及分布影响下的氧化铝纤维烧结晶粒长大的相场模拟
张鲁,刘陆群,唐赛,马运柱,刘文胜
(中南大学 轻质高强国家级重点实验室,长沙 410083)
采用相场法对溶胶凝胶法制备氧化铝纤维的高温烧结中α-Al2O3晶粒的生长进行仿真模拟,并结合实验,研究不同烧结温度和不同初始尺寸的α-Al2O3晶粒长大行为及动力学规律。相场模拟和实验结果均表明,在 1 200~1 500 ℃烧结温度范围内,晶粒生长速率随烧结温度升高而明显增大,其中1 400~1 500 ℃温度区间内晶粒生长速率最快;初始晶粒尺寸越细小,晶粒生长速率越快。模拟结果显示,初始α-Al2O3晶粒尺寸不均匀性增加也会促进晶粒长大。
相场法;氧化铝;晶粒长大;烧结;孔隙
氧化铝(Al2O3)纤维具有高强度、耐高温、耐腐蚀等特性,在极端高温环境中也表现出优异的稳定 性[1−2],可用来提升复合材料的强度和用作航天器的热防护材料。NextelTM610纤维组成相为α-Al2O3,抗拉强度达3.2 GPa[3],高于NextelTM720纤维,是目前强度最高的Al2O3纤维,具有广泛的应用前景。溶胶凝胶法是制备Al2O3纤维的常用方法[4−6]。溶胶凝胶法制备氧化铝纤维主要包括溶胶的制备、浓缩纺丝、脱脂、高温烧结等。随着高温烧结的进行,非晶相先转化为γ-Al2O3,最终转变为α-Al2O3,而相转变得到的α-Al2O3为极细的纳米晶粒,在烧结过程中晶粒逐步长大,从而降低Al2O3纤维产品性能,缩短服役周期;但同时烧结体中的孔洞发生收缩,实现烧结致密化,有利于提高产品性能。因此控制烧结过程中α-Al2O3晶粒组织演化成为NextelTM610纤维制备的关键和难点。烧结过程中决定α-Al2O3晶粒尺寸的要素主要为烧结温度和初始原位生成的α-Al2O3晶粒尺寸及其分布。温度变化会改变材料的物质迁移速率等参量,从而对最终纤维材料的组织产生较大影响,因此在Al2O3纤维的制备中可通过调节烧结温度和保温时间来控制晶粒的生长。采用相场法研究烧结温度对α-Al2O3晶粒长大的影响时,由于模型构造的限制,只考虑温度对物质迁移的作用。烧结温度应高于γ-Al2O3到α-Al2O3的相变温度(通常在1 200 ℃以上),否则α-Al2O3形核率过低,γ-Al2O3向α-Al2O3转变不充分,先形成的α-Al2O3晶粒粗大。若烧结温度过高(高于 1 500 ℃),则晶粒生长过快,得不到预期大小的α-Al2O3晶粒。因此,需要对不同烧结温度下α-Al2O3晶粒长大动力学进行系统性研究,以确定合适的烧结温度和烧结时间。除了控制烧结温度以外,由γ-Al2O3转变而来的初始Al2O3晶粒的尺寸及尺寸分布对烧结后Al2O3纤维的晶粒尺寸也有影响。有人在制备Al2O3纤维前驱体时添加形核剂以促进Al2O3的形核[7],并通过调整形核剂的粒度、含量及种类等来调节Al2O3的形核数量,从而调节α-Al2O3晶粒的初始尺寸及尺寸分布。在NextelTM610纤维制备中常加入0.7%(质量分数)的Fe2O3作为形核剂,使α-Al2O3晶粒数量明显增加,初始晶粒尺寸细小且尺寸分布均匀[8]。研究在不同烧结温度下和不同初始特征的α-Al2O3晶粒长大动力学,可进一步加深对高温下α-Al2O3晶粒长大规律的认识,从而更好地控制烧结过程中α-Al2O3晶粒长大,得到具有合适晶粒尺寸和尺寸分布的NextelTM610纤维。
高温烧结为涉及多种物质迁移及多项因素交叉作用的复杂过程。实验研究中对烧结组织只能观察到静态结果,无法获得整个演化过程的动态结果,因而难以对某些微观结构演变的机理进行合理解释,采用计算机仿真模拟能有效弥补实验研究的不足。相场法是一种无需跟踪界面位置,且能耦合多个场变量的计算模拟方法,广泛应用于烧结过程中材料微观组织演变的研究[9−11]。烧结过程的相场模拟方法在近20年获得快速发展,取得丰硕的研究成果[12−15]。烧结过程的相场模型不断被优化,使其能在考虑刚性球体的运 动[16]、不同颗粒大小[17]、各向异性[18−19]、压力[20]以及温度梯度场[21]等条件下对烧结组织进行描述。本文采用KAZARYAN等[22]提出的多序参量模型,针对溶胶凝胶法制备NextelTM610纤维的高温烧结阶段,考虑烧结时物质迁移及热力学因素的作用,耦合Al2O3实际的物料参数,模拟烧结过程中原位生成的α-Al2O3晶粒在不同烧结温度和不同晶粒尺寸及尺寸分布下的长大规律,并通过实验对模拟结果进行验证。可为溶胶凝胶法制备Al2O3纤维时形核剂的添加及烧结温度的设定提供一定的指导。
1 相场模型与实验
1.1 模型
本研究采用的相场烧结模型包含2个场变量:一个为密度场(),在所有固相处取值均为1,气相处均为0,用以区分不同相;另一个为相场序参量(η) (为晶粒总数),在第个晶粒处η=1,其他晶粒处η=0,用以表征不同的晶粒。通过上述场变量构造自由能密度,包括体自由能、表面能和晶界能等3项,计算公式如下:
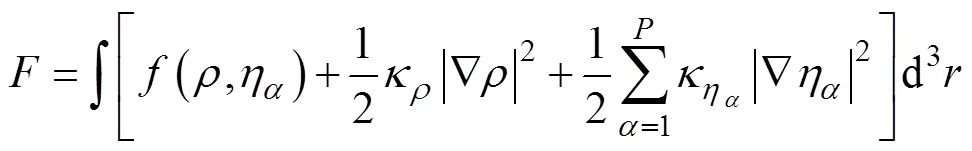
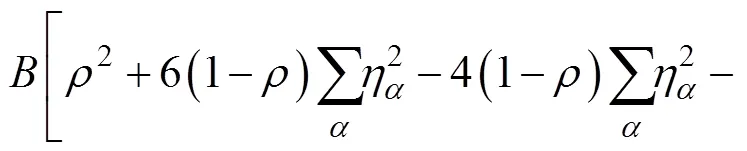
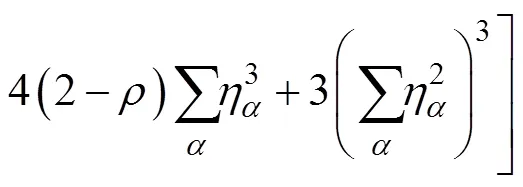
式中:为常数。密度场为保守场,可通过Cahn–Hilliard方程进行变分求解:
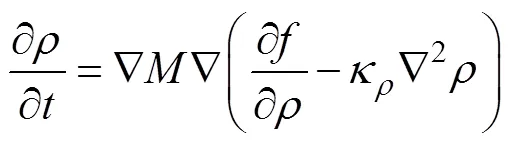

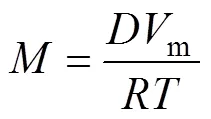
式中:为扩散系数;m为Al2O3的摩尔体积,本文假定m为常数;为摩尔气体常数;为温度。扩散系数综合耦合多个扩散机制[16]:
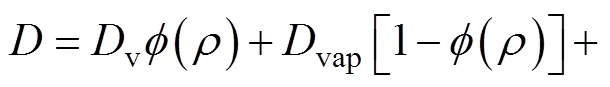
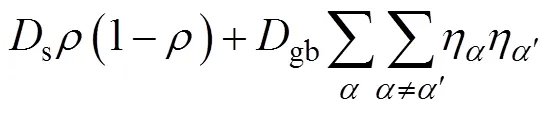
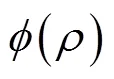
相场序参量η为非保守量,符合Allen-Cahn方程的求解:
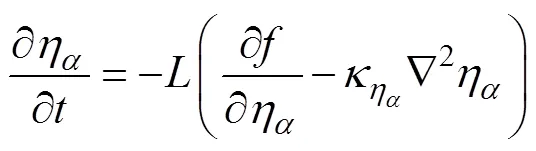
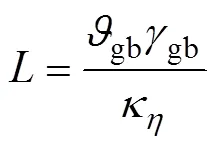
1.2 模型参数
本文通过构建包含多个不规则晶粒的初始微观组织,研究烧结过程中多晶粒组织的晶粒长大现象。如图1所示,在初始条件中加入随机分布的孔洞,呈黑色规则圆形,采取2 nm×2 nm的模拟网格,界面厚度取3个网格数,为6 nm。
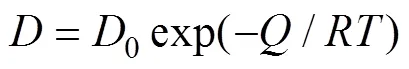
1.3 溶胶凝胶法制备α-Al2O3纤维
所用原料为Al2O3粉末(纯度>99.5%)、甲酸(≥99%)、乙酸(≥99.5%)、硝酸(≥65%),以及纯Fe(NO3)3·9H2O和NH4HCO3,均来自阿拉丁试剂(上海)有限公司。
用纯Fe(NO3)3·9H2O和NH4HCO3制备铁溶胶。 首先制备Fe(NO3)3·9H2O溶液 (Fe(NO3)3·9H2O和去离子水的质量比为1:23.5)和NH4HCO3溶液 (NH4HCO3和去离子水的质量比为1:10),再将Fe(NO3)3∙9H2O溶液缓慢加入Fe(NO3)3溶液中,保证Fe(NO3)3·9H2O和NH4HCO3的物质的量比为2.5:1,用磁力搅拌器搅拌,得到铁溶胶。将Al2O3粉末、甲酸、乙酸、硝酸和去离子水按照物质的量比为1:0.67:0.6:0.36:28的比例混合,在85 ℃下制备成Al2O3前驱体溶胶。
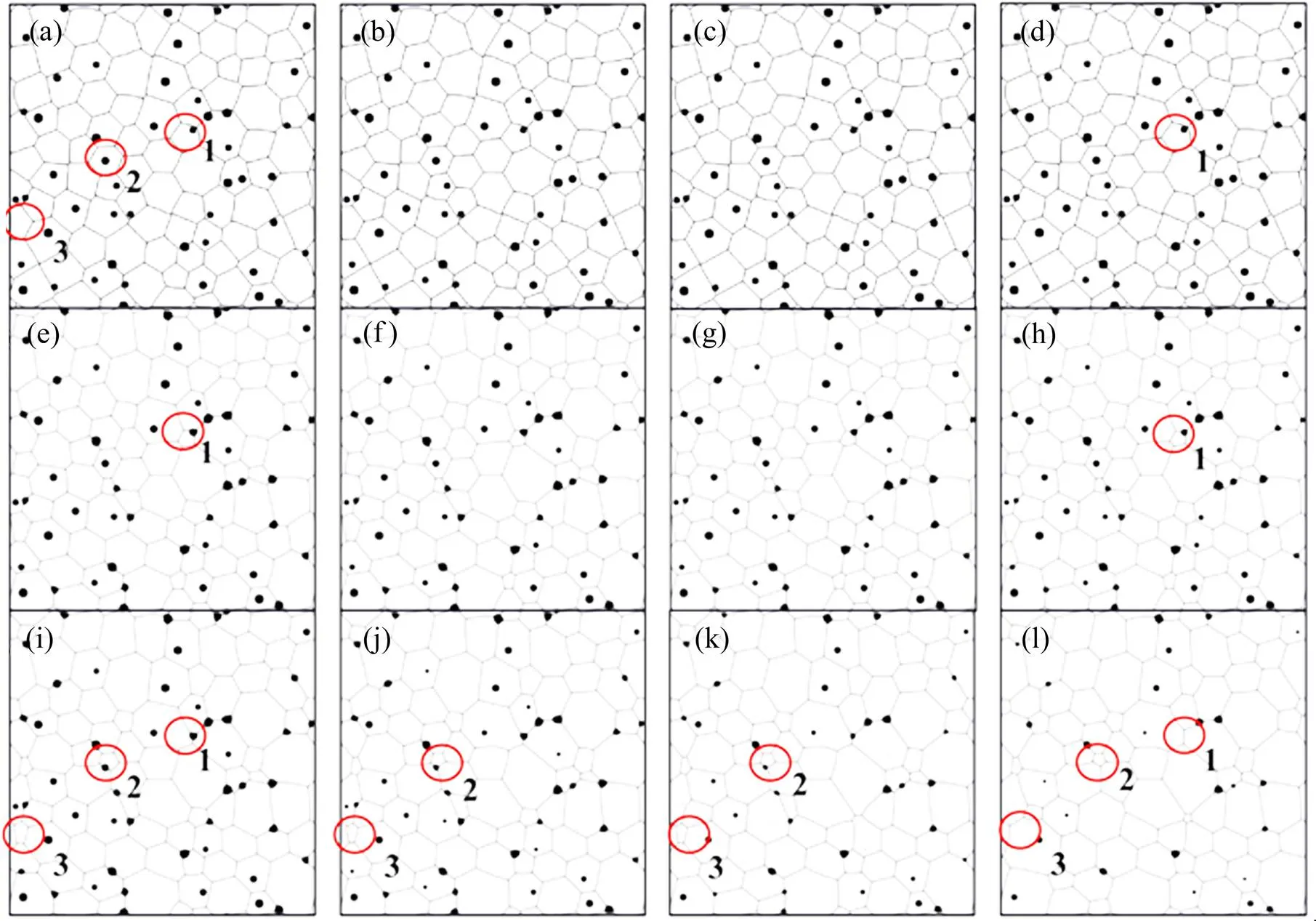
图1 相场模拟的不同温度烧结过程中Al2O3晶粒形貌变化
(a), (e), (i)=1 200 ℃,=0, 200 and 400 s respectively; (b), (f), (j)=1 300 ℃,=0, 200 and 400 s respectively;(c), (g), (k)=1 400 ℃,=0, 200 and 400 s respectively; (d), (h), (l)=1 500 ℃,=0, 200 and 400 s respectively
取13.14 g铁溶胶形核剂加入到150 g Al2O3前驱体溶胶中,搅拌,得到前驱体。用旋转蒸发仪(上海贤德实验仪器有限公司)对前驱体溶胶进行浓缩,得到适合纺丝(黏度为50~200 (Pa·s))的溶胶。通过自制纺丝机干法纺丝制成连续的前驱体纤维,剪成合适长度,然后在室温以2 ℃/min的升温速率升至500 ℃(约4 h),在此升温过程中完成预烧,随后冷却至室温。将预烧后的前驱体纤维分别放入已升至目标温度(分别为1 200、1 300、1 400和1 500 ℃)的管式炉(合肥贝意克公司,BTF-1600C- IV-SL)内烧结6 min,随炉冷却至室温后取出,得到Al2O3纤维。为了研究不同初始尺寸和不同尺寸分布的Al2O3晶粒在高温烧结过程中的长大现象,在Al2O3溶胶中分别加入40、60和80 ℃下制备的铁溶胶,获得不同胶粒尺寸的铁溶胶。其原理在于温度越高,铁离子水解程度和水解物的聚合程度越高,更多的离子或小分子聚集形成粒度更大的胶粒团簇,与Al2O3溶剂混合后可改变Al2O3晶核数密度,从而得到不同的Al2O3形核晶粒尺寸。
用日本JEOL公司生产的JEM-2100F扫描电镜(SEM)观察Al2O3纤维的截面形貌。
2 结果与讨论
2.1 烧结温度的影响
在1 200~1 500 ℃范围内每隔100 ℃设置一个模拟温度,初始晶粒的尺寸分布均为(50±20) nm,得到不同温度烧结过程中Al2O3组织形貌随烧结时间的变化,如图1所示。图1中的1、2、3号圈分别为孔洞在晶界上、晶粒内、晶粒外的3种不同晶粒。从图1可知,1号圈内的晶粒在温度为1 200 ℃和1 500 ℃下都随时间延长而逐渐缩小直至消失。在=200 s时,在1 500 ℃烧结的晶粒尺寸小于1 200 ℃烧结的晶粒尺寸;=400 s时,1 500 ℃下晶粒消失后形成的晶界更长。随烧结时间延长,2号圈内的晶界迁移至孔洞处,在=400 s时,1 500 ℃烧结的晶粒尺寸更小且孔洞已经消失。=400 s时,在1 500 ℃烧结的3号圈内晶粒已消失,而在其他烧结温度下还未完全消失。上述结果表明在1 500 ℃烧结能有效促进晶粒合并与长大。图2(a)所示为相场模拟的不同烧结温度下Al2O3平均晶粒尺寸随保温时间的变化。由图可见当烧结温度为1 500 ℃时,晶粒的平均尺寸增长最快;1 200 ℃烧结时,晶粒平均尺寸的增长速度明显低于其他烧结温度,这表明在1 200 ℃下晶粒合并和生长速度最慢,原因是较低温度下物质迁移速度较慢。从图1还观察到1号圈内存在孔洞的晶界在晶粒缩小的过程中位置保持不变,晶粒缩小是由其他方向的晶界迁移导致的;2号圈内晶粒刚开始的缩小是所有晶界迁移的结果,当晶界迁移到孔洞所在位置时便不再移动。
图3所示为溶胶凝胶法制备Al2O3纤维实验中,烧结温度对Al2O3纤维截面形貌的影响。统计出在不同温度烧结6 min后的Al2O3平均晶粒尺寸,如图2(b)所示。从图3(d)可见烧结温度为1 500 ℃时出现多个大晶粒,其尺寸明显大于其他温度下的晶粒尺寸,这说明随烧结温度从1 400 ℃升至1 500 ℃时,Al2O3纤维中物质迁移的速率明显增大,使晶粒显著长大。图2(a)和(b)所示的模拟结果和实验结果都表明随烧结温度升高,Al2O3平均晶粒尺寸增加。从图3(d)还看出1 500 ℃烧结试样中存在部分小晶粒,所以图2(b)中1 200~1 400 ℃和1 400~1 500 ℃这2个温度区内,平均晶粒尺寸随温度升高而增大的规律差别不大。图2(a)的相场模拟结果显示在1 500 ℃下晶粒生长明显快于其他温度,与图3(d)中1 500 ℃烧结时出现大晶粒相吻合。因此在制备Al2O3纤维中,烧结温度不 应超过1400℃,以防止晶粒过快长大而影响材料性能。
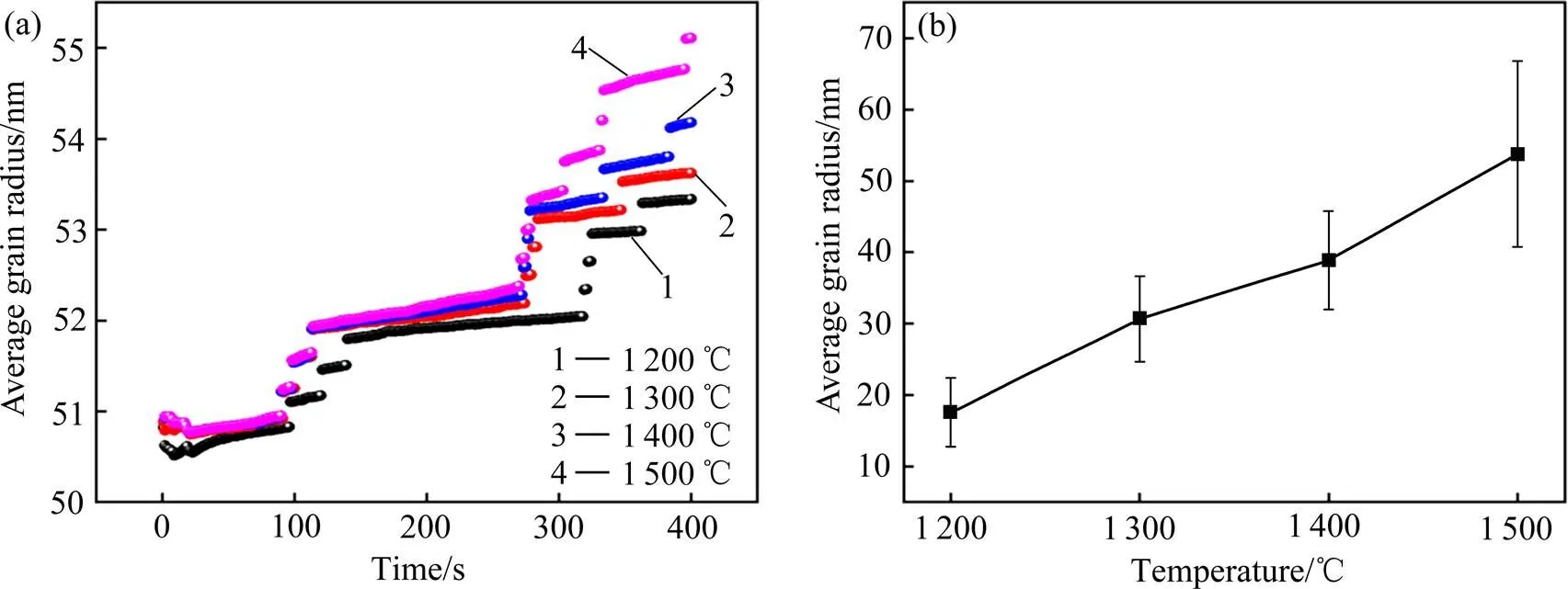
图2 不同温度烧结过程中Al2O3纤维平均晶粒尺寸变化的相场模拟和烧结实验结果
(a) Phase field simulation results; (b) Experimental results (sintering for 6 min)

图3 不同温度烧结6 min后的Al2O3纤维截面SEM形貌
(a) 1 200 ℃; (b) 1 300 ℃; (c) 1 400 ℃; (d) 1 500 ℃
2.2 初始晶粒尺寸分布范围的影响
为了研究烧结后的Al2O3纤维形貌和平均晶粒尺寸随初始形核尺寸分布范围的变化规律,在模拟中初始晶粒数量设置相同、平均晶粒半径50 nm,晶粒平均半径分布范围分别为10、20、30和40 nm,越大表示尺寸分布范围越大。图4所示为模拟得到的具有不同初始尺寸分布范围的α-Al2O3晶粒在 1 400 ℃下烧结过程中组织形貌和平均晶粒尺寸的变化。从图4看出,初始晶粒尺寸分布范围对烧结过程中的晶粒长大有显著影响。具体表现为:初始晶粒尺寸分布越宽,则晶粒越容易长大,在=200 s时,尺寸分布范围较大(=30 nm和=40 nm)的晶粒长大更明显,且发生小晶粒被大晶粒“吞并”的现象。在=400 s时,与其他3组样品相比,=40 nm的晶粒数量最少,说明该组织中被“吞并”的小晶粒数量最多,导致晶粒粗化。 由图4(e)可知, 烧结过程中, 不同的α-Al2O3晶粒的平均尺寸都在增大,其中为40 nm的样品,晶粒平均尺寸增长最快;而为10 nm和20 nm的晶粒平均尺寸增长明显滞后;≥30 nm的样品,在400 s时平均晶粒半径达到64 nm以上,是为10 nm 和20 nm的平均晶粒尺寸的1.3倍左右。模拟结果符合理论上的晶粒长大过程中晶界向曲率减小方向迁移的规律。根据RIOS等[28]关于晶粒异常长大的分析,大晶粒由于其周围的钉扎作用力更小,易于“吞并”小晶粒而长大,甚至形成异常长大晶粒,模拟结果中晶粒长大的规律与该理论相符。
2.3 初始晶粒尺寸的影响
为了模拟研究α-Al2O3形核后的晶粒尺寸(即初始Al2O3晶粒尺寸)对烧结过程中晶粒生长的影响,设置相同晶粒数、初始晶粒尺寸分布范围为20 nm、平均晶粒尺寸分别为50、100和150 nm的3组初始组织,相场模拟烧结过程中Al2O3组织形貌和晶粒相对半径的变化,结果如图5所示。图中标记的圆圈内为初始平均晶粒尺寸50 nm和150 nm的四晶粒交界处,图5(j)中的相对半径为Al2O3晶粒生长后的平均半径与初始平均半径的比值。从图5发现,四晶粒交界处均趋向于形成更稳定的三叉晶界。初始晶粒尺寸=100 nm和=150 nm的Al2O3晶粒,在烧结过程中 尺寸增长较慢,整体形貌无显著变化,其中=150 nm的晶粒在烧结过程中未发生合并长大。从图5(j)可见,初始尺寸不同的α-Al2O3晶粒在烧结过程中长大速度明显不同,=150 nm的晶粒在400 s内平均尺寸几乎无变化,表明烧结过程中晶粒尺寸基本不发生变化。=100 nm的晶粒尺寸变化也不明显,只有=50 nm的晶粒,在烧结400 s后晶粒尺寸增长1.06倍。原因是小尺寸晶粒的单位面积内界面更多,具有较高的界面能量,生长驱动力更大,导致晶界迁移更频繁。
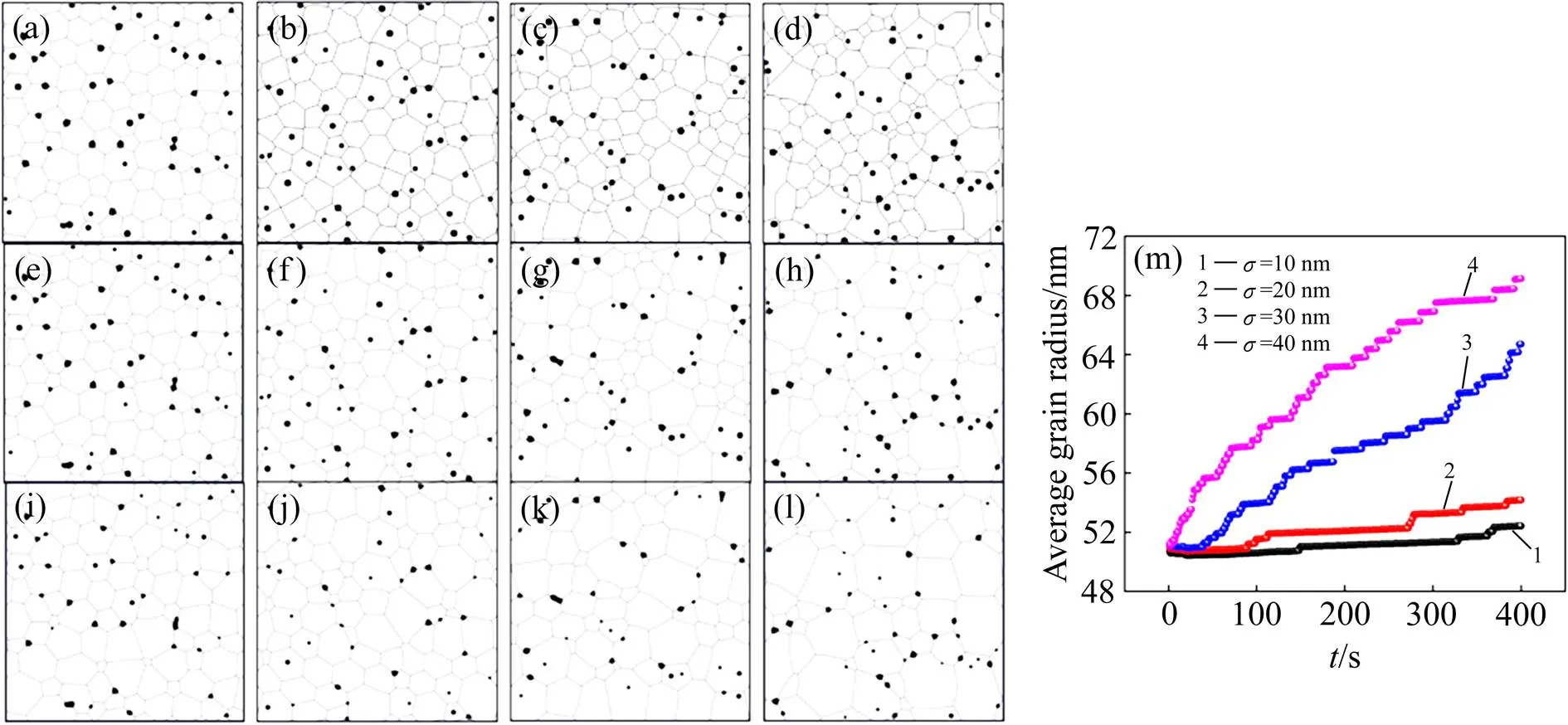
图4 相场模拟的具有不同初始尺寸分布范围σ的Al2O3晶粒在烧结过程中形貌和平均尺寸的变化
(a), (e), (i)=10 nm,=0, 200 and 400 s respectively; (b), (f), (j)=20 nm,=0, 200 and 400 s respectively; (c), (g), (k)=30 nm,=0, 200 and 400 s respectively; (d), (h), (l)=40 nm,=0, 200 and 400 s respectively; (m) Variation of grain size with sintering time
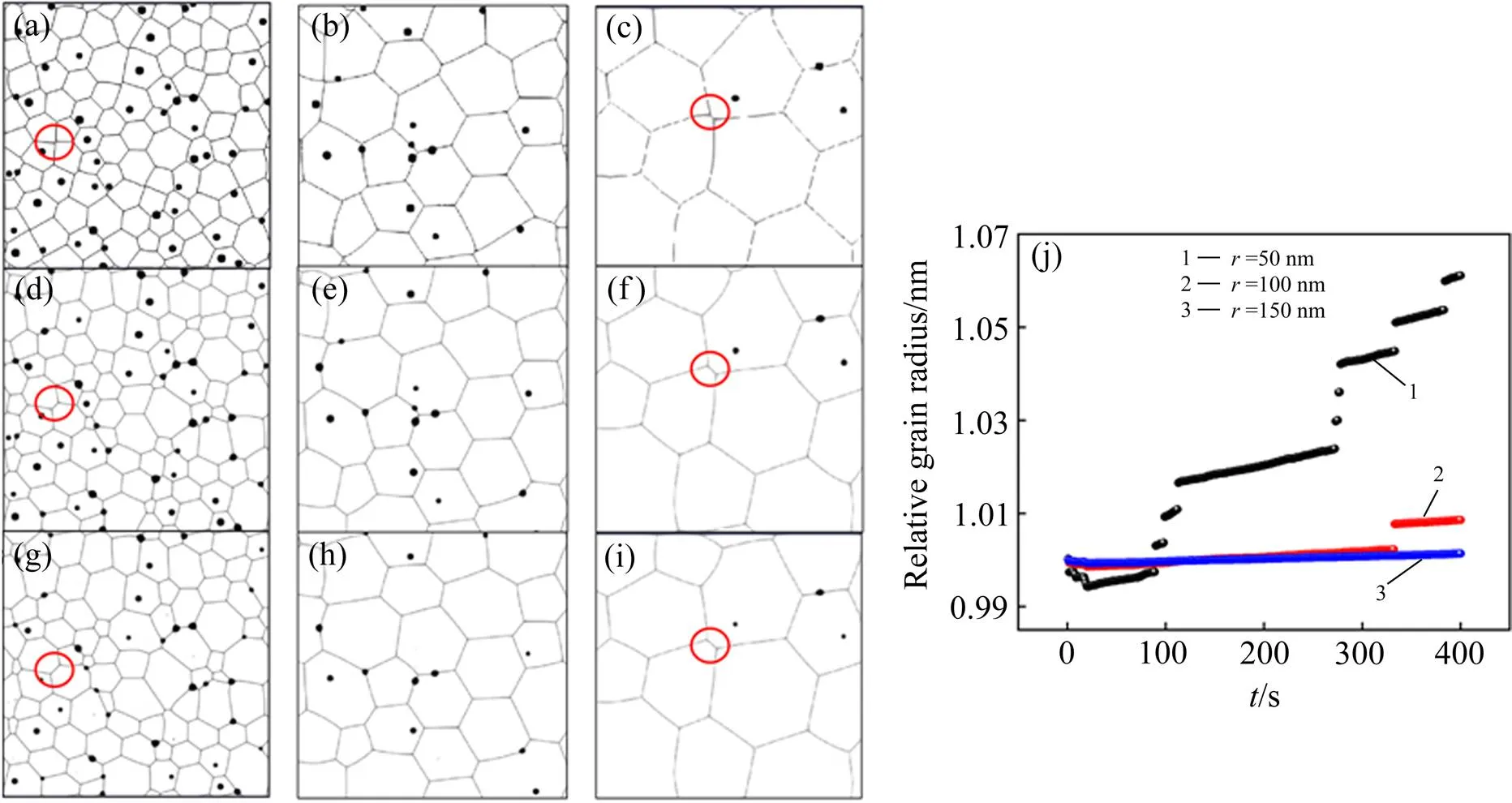
图5 相场模拟的不同初始晶粒尺寸的Al2O3在烧结过程中的形貌和相对半径变化
(a), (d), (g)=50 nm,=0, 200 and 400 s respectively; (b), (e), (h)=100 nm,=0, 200 and 400 s respectively; (c), (f), (i)=150 nm,=0, 200 and 400 s respectively; (j) Al2O3grain size variation
为了验证烧结后不同初始晶粒尺寸的α-Al2O3晶粒尺寸变化,制备Al2O3纤维时,在Al2O3溶胶中分别加入40、60和80 ℃制备的铁溶胶,测得胶粒尺寸(1)分别为3.7、4.7和9.7 nm,然后经过干燥、纺丝、预烧,最后在1 400 ℃分别烧结3 min和5 min,通过扫描电镜观察烧结后Al2O3纤维的组织形貌,结果如图6所示。在3 min内非晶相先转化为γ-Al2O3,最终转变为α-Al2O3,因此以3 min为α-Al2O3发生长大的初始时间点,统计烧结3 min和5 min的平均晶粒尺寸,并计算第3~5 min内晶粒尺寸增长倍数,结果如图7所示。实验结果表明:用40 ℃铁溶胶制备的Al2- O3平均晶粒尺寸在3~5 min内增长近2.5倍,用80 ℃铁溶胶制备的Al2O3平均晶粒尺寸增加幅度最小,证明小尺寸晶粒的热稳定性差,生长速度更快,与模拟结果一致。因为烧结实验中的初始晶粒尺寸(15~30 nm)比相场模拟中设定的初始晶粒尺寸(50~150 nm)小得多,故实验中α-Al2O3晶粒生长速度也快得多。由于界面厚度的限制,为保证模拟的精度,设置初始晶粒尺寸为50 nm以上。虽然小尺寸晶粒的生长驱动力更大,但在一定范围内小尺寸晶粒在烧结后的尺寸仍然相对较小,因此在制备纯α-Al2O3纤维时应保证初始晶粒细小,才能最终获得晶粒细小的高性能α-Al2O3纤维。

图6 不同铁溶胶胶粒尺寸下在1 400 ℃烧结3 min和5 min后的Al2O3 纤维截面SEM形貌
(a), (b) 3.7 nm, sintered for 3 min and 5 min respectively; (c), (d) 4.7 nm, sintered for 3 min and 5 min respectively;(e), (f) 9.7 nm, sintered for 3 min and 5 min respectively
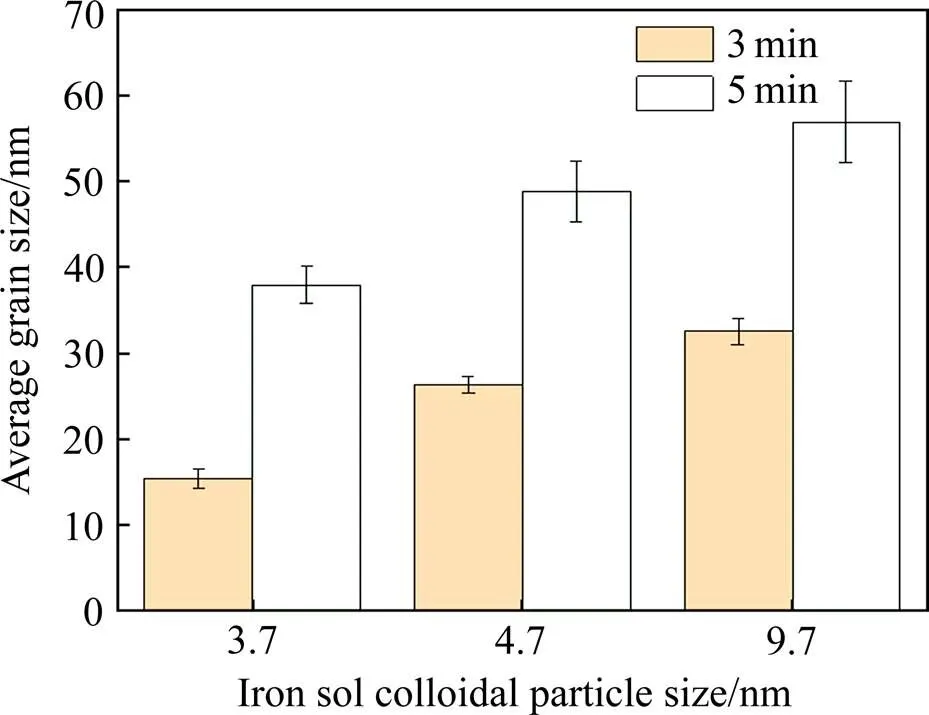
图7 不同铁溶胶胶粒尺寸下在1 400 ℃烧结3min和5 min的Al2O3纤维平均晶粒尺寸
3 结论
1) 采用溶胶凝胶法制备纯α-Al2O3纤维,相场模拟与实验结果表明,在1 200~1 500 ℃烧结温度范围内,Al2O3晶粒尺寸随烧结温度升高而增大,特别是在1 400~1 500 ℃范围内晶粒尺寸增加幅度更大。因此,为了控制Al2O3晶粒尺寸,烧结温度不应超过1 400 ℃。
2) Al2O3初始晶粒尺寸越小,烧结时晶粒长大速度越快;与初始晶粒尺寸分布范围大的晶粒相比,尺寸均匀的Al2O3晶粒生长更慢,有利于提高纤维的热稳定性。故在实际制备中应选择合适的形核剂和制备工艺,尽量确保形核剂的胶粒细小且尺寸均匀,提高α-Al2O3晶粒的形核率和晶核分布均匀性,以得到尺寸细小且大小均匀的初始Al2O3晶粒。
[1] 袁源. 耐高温陶瓷材料的研究现状[J]. 中国科技信息, 2007(18): 104−106.
YUAN Yuan. Research status of high temperature resistant ceramic materials[J]. China Science and Technology Information, 2007(18): 104−106.
[2] 张勇, 何新波, 曲选辉, 等. 超高温材料的研究进展及应用[J]. 材料导报, 2007, 21(12): 60−64.
ZHANG Yong, HE Xinbo, QU Xuanhui, et al. Research progress and application of ultra high-temperature materials[J]. Materials Review, 2007, 21(12): 60−64.
[3] 陈蓉, 才鸿年. 氧化铝长纤维的性能和应用[J]. 兵器材料科学与工程, 2001, 24(4): 70−72.
CHEN Rong, CAI Hongnian. Performance and application of alumina long fiber[J]. Ordnance Material Science and Engineering, 2001, 24(4): 70−72.
[4] SAKKA S. Current and future possibilities of sol-gel process[J]. Transactions of the Indian Ceramic Society, 2005, 64(1): 13−19.
[5] TANH B, GUO C S. Preparation of long alumina fibers by sol-gel method using malic acid[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(7): 1563−1567.
[6] ROQUE-RUIZ J H, MEDELLíN-CASTILLO N A, REYES-LÓPEZ S Y. Fabrication of α-alumina fibers by sol-gel and electrospinning of aluminum nitrate precursor solutions[J]. Results in Physics, 2019, 12: 193−204.
[7] LI X D, XUH N, WANG Q, et al. Control of continuous α-Al2O3fibers by self-seeding and SiO2-sol doping[J]. Ceramics International, 2019, 45(9): 12053−12059.
[8] LIU L Q, WANG J, MA Y Z, et al. Preparation of continuous alumina fiber with nano grains by the addition of iron sol[J]. Materials, 2020, 13(23): 1−14.
[9] KOBAYASHI R, WARREN J A, CARTER W C. A continuum model of grain boundaries[J]. Physica D (Nonlinear Phenomena), 2000, 140(1/2): 141−150.
[10] CHIRRANJEEVI B, ABINANDANAN T, GURURAJAN M. A phase field study of morphological instabilities in multilayer thin films[J]. Acta Materialia, 2009, 57(4): 1060−1067.
[11] CHEN L Q, YANG W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters: The grain-growth kinetics[J]. Physical Review B, 1994, 50(21): 15752−15756.
[12] JING X N, ZHAO J H, HE L H. 2-D phase field simulation of coupled pore and grain topological evolution during final stage sintering[J]. Materials Science and Engineering A, 2003, 21: 170−173.
[13] ASP K, ÅGREN J. Phase-field simulation of sintering and related phenomena–A vacancy diffusion approach[J]. Acta Materialia, 2006, 54(5): 1241−1248.
[14] DENG J. A phase field model of sintering with direction-dependent diffusion[J]. Materials Transactions, 2012, 53(2): 385−389.
[15] SUDIPTA B, DANIEL S, VIKAS T. Implementation of a phase field model for simulating evolution of two powder particles representing microstructural changes during sintering[J]. Journal of Materials Science, 2018, 53(8): 5799−5825.
[16] WANG Y U. Computer modeling and simulation of solid-state sintering: A phase field approach[J]. Acta Materialia, 2006, 54(4): 953−961.
[17] KUMAR V, FANG Z, FIFE P. Phase field simulations of grain growth during sintering of two unequal-sized particles[J]. Materials Science and Engineering A, 2010, 528(1): 254−259.
[18] BISWAS S, SCHWEN D, WANG H, et al. Phase field modeling of sintering: Role of grain orientation and anisotropic properties[J]. Computational Materials Science, 2018, 148: 307− 319.
[19] SHINAGAWA K, MAKI S, YOKOTA K. Phase-field simulation of platelike grain growth during sintering of alumina[J]. Journal of the European Ceramic Society, 2014, 34(12): 3027−3036.
[20] DZEPINA B, BALINT D, DINI D. A phase field model of pressure-assisted sintering[J]. Journal of the European Ceramic Society, 2019, 39(2/3): 173−182.
[21] YANG Y, OYEDEJI T D, KÜHN P, et al. Investigation on temperature-gradient-driven effects in unconventional sintering via non-isothermal phase-field simulation[J]. Scripta Materialia, 2020, 186: 152−157.
[22] KAZARYAN A, WANG Y, PATTON B R. Generalized phase field approach for computer simulation of sintering: incorporation of rigid-body motion[J]. Scripta Materialia, 1999, 41(5): 487−492.
[23] HÖTZER J, SEIZ M, KELLNER M, et al. Phase-field simulation of solid state sintering[J]. Acta Materialia, 2019, 164: 184−195.
[24] MCHALE J, AUROUX A, PERROTTA A, et al.Surface energies and thermodynamic phase stability in nanocrystalline aluminas[J]. Science, 1997, 277(5327): 788−791.
[25] TANG X, LAGERLÖFK P D, HEUER A H. Determination of pipe diffusion coefficients in undoped and magnesia‐doped sapphire (α-Al2O3): A study based on annihilation of dislocation dipoles[J]. Journal of the American Ceramic Society, 2003, 86(4): 560−565.
[26] CHOCKALINGAM K, KOUZNETSOVA V G, VANDERSLUIS O, et al. 2D Phase field modeling of sintering of silver nanoparticles[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 312: 492−508.
[27] AHMED K, YABLINSKY C A, SCHULTE A, et al. Phase field modeling of the effect of porosity on grain growth kinetics in polycrystalline ceramics[J]. Modelling and Simulation in Materials Science and Engineering, 2013, 21(6): 065005.
[28] RIOS P. Abnormal grain growth development from uniform grain size distributions[J]. Acta Materialia, 1997, 45(4): 1785− 1789.
Phase field simulation of grain growth in alumina fiber sintering under the influences of temperature, grain size and distribution
ZHANG Lu, LIU Luqun, TANG Sai, MA Yunzhu, LIU Wensheng
(National Key Laboratory of Science and Technology on High-strength Structural Materials, Central South University, Changsha 410083, China)
The phase field method was used to simulate the growth of pure α-Al2O3grain generated in situ during high temperature sintering process of alumina fiber prepared by the sol-gel method. Combined with experiments, study the growth behavior and dynamics of α-Al2O3grains at different sintering temperatures and different initial Al2O3grain size in the high temperature sintering stage was studied. Both phase field simulation and experimental results show that in the sintering temperature range of 1200−1 500 ℃, the grain growth rate increases significantly with the increase of the sintering temperature, and the grain growth rate is the fastest in the temperature range of 1 400−1 500 ℃. The smaller the initial grain size, the greater the grain growth rate. The simulation result shows that the increasing unevenness of grain size can also promote grain growth.
phase field method; alumina; grain growth; sintering; pore
TB321
A
1673-0224(2021)04-320-09
国家自然科学基金资助项目(U20A20240)
2021−01−29;
2021−03−19
马运柱,教授,博士。电话:0731-88877825;E-mail: zhuzipm@csu.edu.cn
(编辑 汤金芝)

