One Class of the Least Congruences on Completely Regular Semigroups
ZHANG Jiangang(张建刚), SHEN Ran(申 冉)
1 Department of Mathematics, Shanghai Normal University, Shanghai 200234, China
2 College of Science, Donghua University, Shanghai 201620, China
Abstract: Congruence is a very important aspect in the study of the semigroup theory. In general, the Kernel-trace characterizations, Green’s relations and subvarieties are main tools in the consideration of congruences on completely regular semigroups. In this paper, we give one class of congruences on completely regular semigroups with the representation of wreath product of translational hulls on completely simple semigroups. By this new way, the least Clifford semigroup congruences on completely regular semigroups are generalized.
Key words: completely regular semigroup; Clifford congruence; translational hull; wreath product; orthogroup
Introduction
The class of completely regular semigroups coincides with the class of semigroups which are unions of groups. A semigroup is completely regular if and only if it is a semilattice of completely simple semigroups. And a completely simple semigroup is isomorphic to a Rees Matrix semigroup[1-2]. It is complicated to find how the higher semilattice classes act on the lower semilattice classes. To solve the problem, Petirch[3-4]considered the translational hull of a completely simple semigroup and gave it a wreath product representation. It was useful in the research of the structure of a completely regular semigroup. The authors further researched the wreath product representation and got the structures of some subclasses of completely regular semigroups[5-9]. Congruence is a very important aspect in the study of the semigroup theory. In general, the Kernel-trace characterizations, Green’s relations (L, R, H, D, J) and subvarieties are main tools in the consideration of congruences on completely regular semigroups[1-2, 10-16].
In this paper, we get one class of congruences on completely regular semigroups by the representation of wreath product of the translational hull of a completely simple semigroup. This is a new way to study the congruences of completely regular semigroups. And we generalize the least Clifford semigroup congruences on completely regular semigroups.

If Green’s relation H is a congruence on a completely regular semigroupS, thenSis called a cryptogroup. Furthermore, a cryptogroupSis a L-cryptogroup ifS/H belongs to the class L of bands. Denote the set of idempotents ofSbyE(S).Sis called an orthogroup ifE(S) is a subsemigroup ofS. An orthodox cryptogroup is an orthocryptogroup. Further,a semigroupSis called a Clifford semigroup if it is a (strong) semilatticeYof groups. It is obvious that a Clifford semigroupSis orthodox and cryptic, and Green relations H=J is the least semilattice congruence on it. LetSbe a completely regular semigroup. For anya∈S, denote the group inverse ofaand the identity ofHabya-1anda0respectively. A completely regular semigroupSis a cryptogroup if and only if (ab)0=(a0b0)0for anya,b∈S. For any binary relationθonS,θ*denotes the congruence generated byθ,i.e.,θ*is the least congruence containingθ.
All the other terminologies and notations which are not explained can be found in Refs. [1-2,11].
1 Some Preliminaries
In this section, we recall the representation of wreath product of left, right translations and bitranslations of completely simple semigroups given by Petrich[3]. The representation of wreath product is one of important tools in the study of completey regular semigroups. By the representation, the authors investigated some properties of bitranslations of completely simple semigroups[5].
LetSbe a semigroup andx,ybe arbitrary elements ofS. A mapσonS, written on the left, is a left translation ifσ(xy)=(σx)y; a mapρonS, written on the right, is a right translation if (xy)ρ=x(yρ); a left translation σ and a right translationρare linked ifx(σy)=(xρ)yin which the pair (σ,ρ) is a bitranslation. The setΣ(S) of all left translations ofSis a semigroup under the composition (σσ′)x=σ(σ′x); the setP(S) of all right translations ofSis a semigroup under the compositionx(ρρ′)=(xρ)ρ′; the subsemigroupΩ(S) ofΣ(S) ×P(S) consisting of all bitranslations is the translational hull ofS. Specially,σaandρaare linked obviously, whereσax=axandxρa=xa, for somea∈S.
LetT=M(I,G, Λ;P) be a completely simple semigroup andσ∈Σ(T),ρ∈P(T).By the results[3], there existφ∈ζ(I),ψ∈ζ′(Λ) andu∈GI,v∈ΛGsuch that for any (i,g,λ)∈T,
σ(i,g,λ)=(φi, (ui)g,λ), (i,g,λ)ρ=
(i,g(λv),λψ),
(1)
where J(I)(J ′(Λ)) is the semigroup of all transformations on the setI(Λ), andGI(ΛG) denotes the semigroup of all functions fromI(Λ) intoGunder the compositions (u·u′)x=(ux)(u′x) for allu,u′∈GIandx∈Iandy(v·v′)=(yv)(yv′) for allv,v′∈ΛG,y∈Λ.
Denote the set J(I) ×GIwith the multiplication (φ,u)(φ′,u′)=(φφ′,uφ′·u′) by J(I)wlG, where (uφ′)x=u(φ′x) for allx∈I. Dually, denote the setΛG× J ′(Λ) with the multiplication (v,ψ)(v′,ψ′)=(v·ψv′,ψψ′) byGwrJ ′(Λ), wherey(ψv′)=(yψ)v′ for ally∈Λ.

→ (φ, u) andχ

are semigroup isomorphisms.

(λv)p(λψ)i=pλ(φi)(ui), for anyi∈I,λ∈Λ.
(2)
If (φ,u) and (v,ψ) satisfy formula (2), we say that (φ,u) and (v,ψ) are linked. The set of all linked pairs in (J(I)wlG) × (GwrJ ′(Λ)) is denoted by Δ(T), and its element ((φ,u), (v,ψ)) is denoted by [φ,u,v,ψ].And the wreath product of Δ(T) is given by
[φ,u,v,ψ][φ1,u1,v1,ψ1]=
[φφ1,uφ1·u1,v·ψv1,ψψ1].

[φ,u,v,ψ]
is an isomorphism.
We will consider the idempotents ofΩ(T) by the representation of wreath product in the next lemma.

ProofIfω2=ω, thenσ2=σandρ2=ρ. By Lemma 1,σ2=σif and only if (φ2,uφ·u) =(φ,u) if and only ifφ2=φanduφ=〈ι〉, whereιis the identity of the groupG. By formula (2), for anyi,j∈I,λ∈Λ,
then

(3)
We takej=φiin Eq. (3). Since (i,φi)∈Kerφfor anyi∈Ianduφ=〈ι〉, then


2 Main Results
The study of the congruences on semigroups is an important way to characterize their structures. The least inverse congruences on completely regular semigroups were discussed by various authors[1-2, 10]. In this section, one class of congruences on completely regular semigroups are given by the representation of wreath product of the translational hulls, and then we generalize the least Clifford semigroup congruences on completely regular semigroups.
Suppose thatNis a normal subgroup of a groupGandg,h∈G. Ifgh-1∈N, we denoteg≡h(modN). SinceNis normal, it is easy to see ifg≡h(modN), thenh≡g(modN) and ifa≡b(modN),c≡d(modN), we can getac≡bd(modN) for anya,b,c,d∈G.
From Lemma 5 to Lemma 8, we always suppose thatS=∪α∈YSαis a completely regular semigroup andα,β∈Ywithα≥β.

ProofBy formula (2), for anyj∈Iβ, we have (1βva)p(1βψa)j=p1β(φaj)(uaj).So

by the normality ofPβ. In particular,ua1β=(1βva)p(1βψa)1β=(1βva).And so
uaj=ua1βp(1βψa)j,
and henceuaj≡ua1β(modNβ). Similarly,μva≡ 1βva(modNβ) can be proved.
As special cases, we have the following two lemmas.
Lemma6For anyeiλ∈E(Sα),ueiλj≡ιβ(modNβ) andμveiλ≡ιβ(modNβ) for anyj∈Iβ,μ∈Λβ.
ProofSinceeiλ∈E(S), then (σeiλ,ρeiλ)=(σeiλ,ρeiλ)2is a bitranslation ofSβ. By Lemma 4, we have for anyμ∈Λβ,

and henceueiλj≡ιβ(modNβ) for anyj∈Iβ. Similarly, we can prove thatμveiλ≡ιβ(modNβ) for anyμ∈Λβ.
Lemma7For anyh1α1α∈Sα, h∈Nα, uh1α1α j ≡ ιβ(mod Nβ) and μvh1α1α≡ιβ(modNβ) for anyj∈Iβ,μ∈Λβ.
ProofFor anyi∈Iα,λ∈Λα, since (1α,pλi, 1α)=(1α,ια,λ)(i,ια, 1α)=e1αλei1α, by Lemma 1 and Lemma 6, for anyj∈Iβ,
u(1α, pλi,1α)j=ue1αλei1αj=(ue1αλφei1α·uei1α)j=
ue1αλ(φei1αj)uei1αj≡ιβ(modNβ).
(4)

(5)


or
a=(1α,g, 1α)(1α,pλi, 1α)(1α,g-1, 1α).
By Eqs. (4)-(5), Lemma 5 and Lemma 6, for anyj∈Iβ,

LetS=∪α∈YSαbe a completely regular semigroup. For anya=(i,g,λ),b=(j,h,μ)ofS,θis a congruence onSsatisfyingθ⊆D. Define a relationρonSby
aρb⟺aθbandg≡h(modNα) for some
α∈Y, ifa,b∈Sα.
(6)
By the above definition, we have the following result.

ProofIfaρb, theng≡h(modNα). Suppose thath=ngfor somen∈Nα. Since
On one hand, by Lemma 5 and Lemma 6,
ua1β=uei1αg1α1αλ1β≡ (uei1α1β)(ug1α1α1β)(ue1αλ1β) ≡
ug1α1α1β(modNβ).
Similarly,ub1β≡uh1α1α1β(modNβ).
On the other hand, by Lemma 7,
uh1α1α1β=un1α1αg1α1α1β≡ (un1α1α1β)(ug1α1α1β) ≡
ug1α1α1β(modNβ).
And soua1β≡ub1β(modNβ). Similarly, 1βva≡ 1βvb(modNβ) can be proved.
Now we give the main result of this paper.
Theorem1LetS=∪α∈YSαbe a completely regular semigroup. Then the relationρdefined in formula (6) is a congruence onS.
ProofIt is obvious thatνis an equivalence by the definition. Leta=(i,g,λ),b=(j,h,μ)∈Sαandaρb.Theng≡h(modNα). For anyc∈Sβ, suppose thatac=(k,l,ξ),bc=(k′,l′,ξ′)∈Sαβ.It is clear thatacθbc. Now we will show thatl≡l′(modNαβ).
Since
for anyt∈Iαβ.By Eq. (1) and Lemma 5 we have

Similarly,l′ ≡ub(1αβ)uc(1αβ)(modNαβ). On the other hand,ua(1αβ) ≡ub(1αβ)(modNαβ) by Lemma 8, so we getl≡l′(modNαβ) andacρbc. Similarly, the right compatibility ofρcan be proved. And henceρis a congruence onS.
Lemma9[2]LetT=M(I,G,Λ;P) be a completely simple semigroup. Assume thatPis normalized. LetNbe a normal subgroup ofG, andNcontains all entries ofP, then the relationξdefined onTby
(i,g,λ)ξ(j,h,μ) ifgh-1∈N
is a group congruence onT. Conversely, every group congruence onTcan be constructed.
It is easy to see that ifNis the least normal subgroup ofGgenerated by the elements ofP, then the corresponding group congruence onTis the least one.
At last, we consider some special cases of the congruencesθandρ. The following lemma describes the congruences onSgenerated by Green’s relations.
Lemma10[2]LetSbe a completely regular semigroup. Then
(1) H*is the least band congruence onS.
(2) L*(R*) is the least right(left) regular band congruence onS.
(3) L*∩ R*is the least regular band congruence onS.
(4) L*∨ R*=D is the least semilattice congruence onS.
Theorem2LetS=∪α∈YSαbe a completely regular semigroup.
(1) Ifθ=H*, thenρis the least orthocryptogroup congruence onS.
(2) Ifθ=L*(R*), thenρis the least right(left) regular orthocryptogroup congruence onS.
(3) Ifθ=L*∩ R*, thenρis the least regular orthocryptogroup congruence onS.
(4) Ifθ=L*∨ R*=D, thenρis the least Clifford congruence onS.
ProofFor anyα∈Y, letθ=H*, since H⊆θ⊆D, it is easy to see that everyθ-class is a completely simple subsemigroup ofS. By Theorem 1 and Lemma 9, everyρ-class ofSis the maximum group homomorphism image of the correspondingθ-class ofS.
Leta,b∈S. ThenaH*a0,bH*b0anda0b0H*abH*(ab)0. By the definition ofρ, we know that (aρ)0=a0ρ. We writeT=S/ρ, denote the Green relation H onTby HT. Then
(a0b0)ρHT(ab)ρHT(ab)0ρ
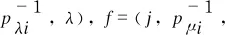

HenceTmust be orthodox, andTis an orthocryptogroup.
By Lemma 9 and Lemma 10,ρis the least orthocryptogroup congruence onS. Similarly, the remainders can be proved.
A completely simple and orthodox semigroup is called a rectangular group.
Lemma11[2]LetT=M(I,G,Λ;P) be a completely simple semigroup. Then the following conditions onTare equivalent.
(1)Tis orthodox.
(2)T≅I×G× Λ, whereIand Λ are given the multiplication of a left and a right zero semigroup, respectively.
(3) IfPis normalized, thenpλi=efor alli∈Iandλ∈Λ, whereeis the identity of the groupG.
LetSbe an orthogroup. Then it is a semilattice of rectangular groups. For anya=(i,g,λ),b=(j,h,μ)∈SandaDb,θis a congruence onSsatisfyingθ⊆D. Define a relationρonSby
aρb⟺aθbandg=h.
(7)
Corollary1Let S be an orthogroup.
(1) Ifθ=H*, thenρis the least orthocryptogroup congruence onS.
(2) Ifθ=L*(R*), thenρis the least right(left) regular orthocryptogroup congruence onS.
(3) Ifθ=L*∩ R*, thenρis the least regular orthocryptogroup congruence onS.
(4) Ifθ=L*∨ R*=D, thenρis the least Clifford congruence onS.
3 Conclusions
The study of congruences on a semigroup is a very important tool in the theory of semigroups. One class of congruences on completely regular semigroups are given by the representation of wreath product of the translational hulls, and then we generalize the least Clifford semigroup congruences on completely regular semigroups in this paper.
 Journal of Donghua University(English Edition)2021年3期
Journal of Donghua University(English Edition)2021年3期
- Journal of Donghua University(English Edition)的其它文章
- Hardware-in-the-Loop Simulation of Vibration Control of Stay Cables with Damper Based on dSPACE System
- Effect of Two Kinds of Similarity Factors on Principal Component Analysis Fault Detection in Air Conditioning Systems
- Abundant Exact Solutions for Differential-Difference Equations Arising in Toda Mechanics
- Linear Dynamical System over Finite Distributive Lattice
- Optimal Reactive Power Compensation of Distribution Network to Prevent Reactive Power Reverse
- Raoultella terrigena RtZG1 Electrical Performance Appraisal and System Optimization
