Linear Dynamical System over Finite Distributive Lattice
DENG Aiping (邓爱平), GONG Xiaoyue (弓晓月), MA Hongcai (马红彩)
College of Science, Donghua University, Shanghai 201620, China
Abstract: A finite dynamical system (FDS) over a lattice L is a pair (S(L), f), where S(L) is a left-L module and f is a mapping from S into itself. The phase space of (S(L), f) is a digraph whose vertex set is S(L) and there is an arc from x to y if y=f(x). Let L be a finite distributive lattice, A an n×n matrix over L, and f(x)=Ax. The structure of the phase space of the FDS (Ln, f) is discussed. The number of limit cycles in the phase space of (Ln, f) is described in Mö bius function. The phase spaces of some invertible, nilpotent, and idempotent FDS (Ln, f)are characterized explicitly.
Key words: finite distributive lattice; linear dynamical system; phase space; limit cycle; rooted in-tree
Introduction
LetLbe a finite lattice with the partial order ≤.For anya,b∈L, the least upper bound and the greatest lower bound ofaandbare denoted bya∨banda∧b, respectively. Let 1 be the greatest element and 0 the least element inL.The lattice (L, ∨, ∧, 1, 0) is a distributive lattice if for anya,b,c∈L, one of the following conditions holds[1-2]:
a∧(b∨c)=(a∧b)∨(a∧c),
a∨(b∧c)=(a∨b)∧(a∨c),
(a∨b)∧c=a∨(b∧c).
The set of allm×nmatrices overLis denoted byMm, n(L). LetLn=Mn, 1(L) andMn(L)=Mn, n(L). Ifaijis the (i,j)-entry ofA, we writeA=(aij). LetATbe the transpose ofA. Then×ndiagonal matrix with diagonal entries all 1sand the others all 0sis called the identity matrix, and denoted byIn. Ifnis clear from context, we simply writeIin place ofIn. SetA0=Ifor anyA∈Mn(L). ForA,B∈Mm, n(L),C∈Mn, l(L), andi=1, 2,...,m,j=1, 2,...,n, we define
A≤Bifaij≤bij,
A∨B=(aij∨bij),
A∧B=(aij∧bij),
aA=(a∧aij),a∈L.
It is easy to check thatDIn=ImD=Dfor anyD∈Mm, n(L).
A dynamical system over a latticeLis a pair (S(L),f), whereS(L) is a left-Lmodule andfis a mapping fromS(L) into itself. The dynamics of (S(L),f) is encoded by its phase spaceG(S(L), f), which is a digraph with vertex setS(L) and there is an arc fromxtoyify=f(x).Ifhandlare the smallest positive integers such thatfh+l(x)=fh(x), then the sequence {fh(x),fh+1(x),...,fh+l-1(x),fh+l(x)} forms a cycle of lengthl, which is called a limit cycle. Cycles of lengthlare calledl-cycles. A vertex in anl-cycle is called a periodic vertex with minimal positive periodl. The limit cycle containing vertexvis denoted byC(v).For each periodic vertexv, the set {v,f-1(v),f-2(v),...} forms an in-tree rooted atv, in notationT(v). In general, the phase spaceG(S(L), f)consists of limit cycles and in-trees attached to vertices of limit cycles.
Dynamical systems over finite rings or fields have been widely studied and applied in engineering, computational biology,etc.[3-7]A basic problem in dynamical system theory is to characterize the system dynamics through the system description. An efficient way is to study the dynamics from its phase space but without enumerating all states and all phase transitions.
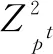
It is natural to consider a dynamical system (Ln,f) over a latticeLand a mappingfthat mapsxintoAxforx∈LnandA∈Mn(L).Comparing with finite rings or finite fields, a finite lattice has not so good properties. Therefore, we focus on a finite distributive latticeLand a mappingf:xAx,A∈Mn(L).Thenfis a linear map[12]. Our aim is to characterize the structure of the phase spaceG(S(L), f), orG(A) for short. Even for a finite distributive latticeL,Lnis not a direct sum of the bijective part and the transient part off.Therefore, the phase space is no longer a product of cycles and trees, which is a fact for finite rings or fields. The non-zero in-degree of a vertex are different, which is determined by not only the matrix and the lattice but also the vertex itself. The in-degree of a vertexyinG(A), denoted byd-(y), is the number of directed edges going tov.Notice thatd-(y) is also the number of solutions to the equationAx=y. For any vertexxofT(v), the height ofxis denoted byh(x) which is the least non-negative integerhsatisfyingAhx=v.The maximum height of these trees is called the height of the graph, and it is denoted byhA.
About the basic notions and results on lattice matrices one may refer to Ref.[13].The properties of matrices on distributive lattices have studied by many authors[14-16]. Some necessary and sufficient conditions for lattice matrices to be revertible or nilpotent were presented[14].The nilpotent matrices on a bounded distributive lattice were studied[17].
We discuss in this paper the length of limit cycles inG(A).The length of each cycle is a divisor of the largest length of all cycles. The relations of the number of cycles with different length can be represented by Möbius function. We characterize the in-tree part for some specific systems such thatfis invertible, nilpotent, or idempotent. The remainder of this paper is organized as follows.
In section 1, we introduce some basic notions and results of the finite distributive lattices and lattice matrices.
In section 2, we give a relationship between the numbers of the limit cycles with different length in Möbius function. We also characterize the phase space for some invertible, nilpotent and idempotent dynamical systems over the latticeL.
In section 3, we summarize the results of this paper.
1 Preliminaries
We present in this section some definitions and preliminary lemmas. Some propositions are obtained for later use.
Definition1[12]Let (L, ∨, ∧, 1, 0) be a finite distributive lattice. The elementb∈Lis called a complement ofa∈Lifa∧b=0 anda∨b=1.
Lemma1[12]Any element with a complement in a distributive lattice has a unique complement.
Definition2[14]A matrixA∈Mn(L) is said to be right invertible (left invertible) ifAB=I(BA=I) for someB∈Mn(L).In this case, the matrixBis called a right inverse (left inverse) ofA.IfAis both right and left invertible, then it is said to be invertible.

i,j=1, 2, …,n.
Lemma3[12]Let (L, ∨, ∧, 1, 0) be a lattice, and letA=(aij) be a matrix inMn(L).ThenAk+t=AkAtfor any non-negative integerskandt.
Lemma4[18]Let (L, ∨, ∧, 1, 0) be a lattice. IfA=(aij) is a matrix inMn(L), then the following statements are equivalent.
(1)Ais right invertible;
(2)Ais left invertible;
(3)Ais invertible;
(4)AAT=I;
(5)ATA=I;
(6)AAT=ATA;
(7)At=Ifor some positive integert.
Lemma5[19]IfA,B∈Mn(L) andAB=I, thenB=ATandBA=I.
The inverse matrix ofAis denoted byA-1.By Lemma 5, we know that ifAis invertible, then its inverse is unique andA-1=AT.
Lemma6[14]Let (L, ∨, ∧, 1, 0) be a finite distributive lattice andA=(aij)∈Mn(L).Then the matrixAis invertible if and only if
or equivalently,
Here we give some results about invertible lattice matrices.
Proposition1IfA∈M2(L) is an invertible matrix, thenAis a symmetric matrix.

Then by Lemma 1, we obtaina12=a21. ThusA=AT.
Proposition2Let(L, ∨, ∧, 1, 0) be a finite distributive lattice. IfA∈Mn(L) is an invertible matrix, thenAis symmetric if and only ifA2=I.
ProofThe result comes directly from Lemma 5.
2 Main Results
In this section we study the phase spaceG(A)of the FDS (Ln,f), wheref(x)=Ax,A∈Mn(L).We give a relationship between the numbers of the limit cycles with different length in Möbius function. We also characterize the phase space for some specific systems such thatfis invertible, nilpotent or idempotent.
2.1 Phase space G(A) for general A∈Mn(L)
Letnidenote the number of limit cycles with lengthi.The set of vectors fixed byAiis denote byF(Ai), that is,F(A)i={x∈Ln|Aix=x}.An element inF(A) is a fixed point of the system. In the phase spaceG(A), a fixed point is a vertex in a 1-cycle. In a linear FDS (Ln,f), it’s clear that the zero vector is always a fixed point.
The setf(Ln)={y∈Ln|∃x∈L,y=f(x)} is called the image off.Here we also denote this image by ImA[12].
Theorem1Let(L, ∨, ∧, 1, 0)be a finite distributive lattice. ForA=(aij)∈Mn(L), assume thath(≥0) andl(≥1) are the minimal integers satisfying the equationAh+l=Ah.Then in the phase spaceG(A),his the maximal height of the trees andlis the maximal length of the limit cycles. The length of each limit cycle is a divisor ofl.
ProofFor any vertexx∈Ln, it holdsAh+lx=Ahx.Theny=AhxsatisfiesAly=y,i.e.,yis a periodic vertex. Thus the height of any vertexxis less than or equal toh.
Sinceh(≥0) andl(≥1) are the minimal integers satisfying the equationAh+l=Ah, there exists a vertexx0∈Lnsuch thatAh+l(x0)=Ah(x0) butAh+l-1(x0)≠Ah(x0), and a vertexx1∈Lnsuch thatAh+l(x1)=Ah(x1) butAh+l-1(x1)≠Ah(x1). Hence the height ofx0ish, and the vertexAh(x1) is in a limit cycle of lengthl.Therefore we finish the proof thathis the maximal height of all trees inG(A), andlis the maximal length of all limit cycles.
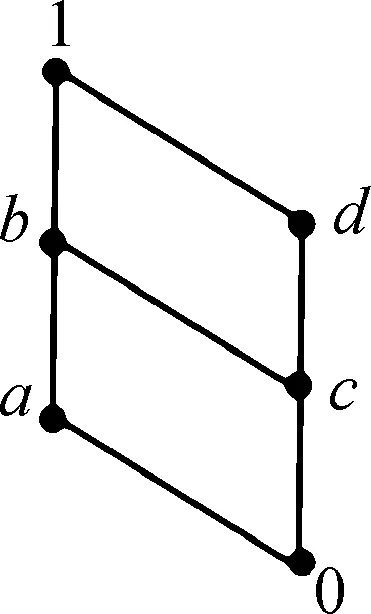
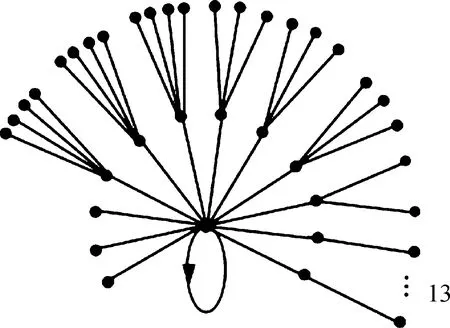
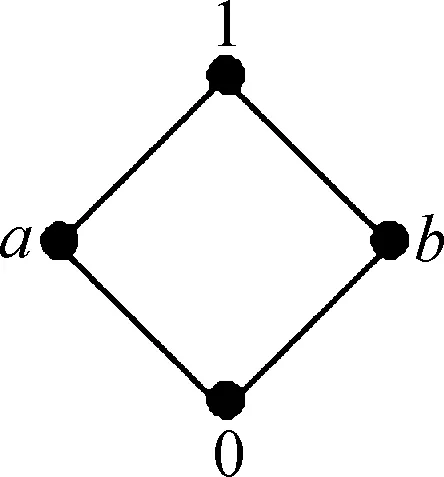
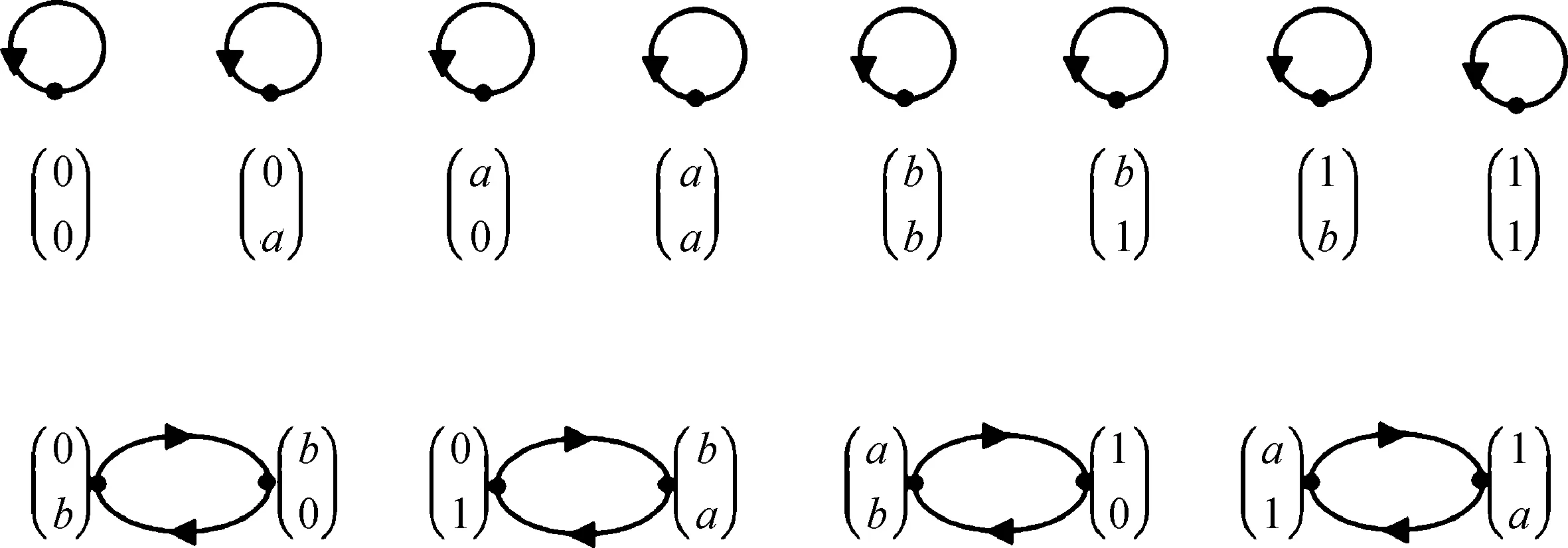
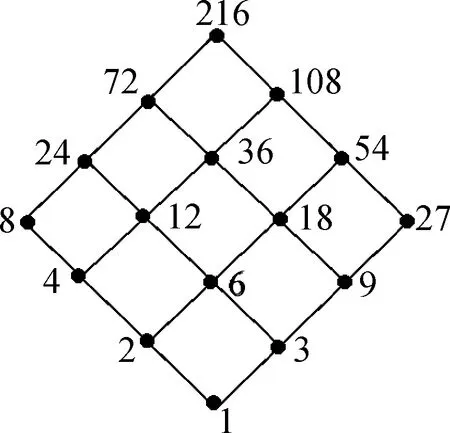
From the above result we know that ImAhconsists of all periodic vertices. Assumeyis in a limit cycle of lengtht.Theny∈ImAh,Aty=yandAiy≠y(0 Supposel=st+r, 0≤r≤t.Sincey∈ImAh, there exists a vertexxsuch thaty=Ah(x). Then It follows fromAiy≠y(0 We usehAandlAto denote the integershandlin the above theorem. Theorem2The number of cycles of lengthtin theG(A) is (5) whereμis Möbius function. ProofNote that ifi|jthenF(Ai)⊂F(Aj).So we have which can be expressed as a matrix equation. (6) wherepiare different primes. Thus Eq.(5) is obtained. In a phase space of a linear FDS over a finite ring or field, the non-zero in-degree of each vertex can be characterized in the Kernel of the mapping[12].However, for a linear FDS over a general lattice the result does not exists any longer. That is because the fact that to a matrix equationAx=yover a lattice the number of solutions for eachymay also depend on the vectoryitself. The following is an example. Example1Consider the phase spaceG(A) of a linear FDS (L3,f) over a latticeL={0,a,b,c,d, 1}.The Hasse diagram ofLis depicted in Fig. 1. The mapping isf:xAx, where the matrix Fig. 1 Lattice L in Example 1 Fig. 2 Component of G(A) in Example 1 with direction of arcs in the tree omitted One checks thatA4=A2, andA3≠A2.Thus we havehA=2,lA=2.In this phase spaceG(A),n1=10 andn2=4.Figure 2 illustrates a component ofG(A) consisting of a limit cycle of length 1 and the in-trees rooted on the cycle. Besides the component above there are 2 cyclesG(A).For instance, there is a 2-cycle (u,w,u), where One checks thatAu=wandAw=u. Now, we discuss the structure of the phase spaceG(A) of the linear FDS (Ln,f) such thatfis an invertible, nilpotent, or idempotent mapping. IfAis an invertible matrix, thenf:Ln→,xAxis an invertible mapping. We call the corresponding system FDS (Ln,f) an invertible system. It is obvious that the phase spaceG(A) of an invertible system consists of limit cycles. We discuss the largest lengthlAof the limit cycles inG(A) in the casesAis symmetric or non-symmetric. At the end of this subsection we show that the system (Ln,f) is a fixed-point system if and only ifAis the identity matrix. First we consider the case thatAis both invertible and symmetric. Example2Consider the phase spaceG(A) of a linear FDS (L2,f) over the latticeL={0,a,b, 1}.The Hasse diagram ofLis depicted in Fig. 3. The mapping isf:xAx, where the matrix Fig. 3 LatticeLin Example 2 Fig. 4 Phase space G(A) in Example 2 Lemma7Let (L, ∨, ∧, 1, 0) be a finite distributive lattice andAan invertible matrix inMn(L).If the set of entries in each row ofAis the same, then the set of entries in each column ofAis the same, and vice versa. ProofWe only show the first part. By exchanging rows and columns in the proof then we prove the second part. Assume the first row ofAis (a1,a2, …,an) . By Eq. (2) in Lemma 6 the greatest lower bound of any two entries is 0. Thus any two nonzero entries in each row must be different. Without loss of generality we assume thata1,a2, …,asare nonzero andas+1=…=an=0 . LetR={a1,a2, …,as} . Then the nonzero entries of thejth column form a subsetCjofR. Next we show thatCj=R(j=1, 2, …,n) and therefore the proof is finished. Similar as above by Eq. (4) in Lemma 6 we know that any two nonzero entries in each column ofAare different. Since the set of entries in each row is the same and eachai∈Roccurs exactly once in each row, eachai∈Roccurs totallyntimes in the matrixA.If one of them, sayai, does not occur in some column, say thejth column, thenaimust occur more than once in another column. This contradicts to Eq. (4). ThusCj=R(j=1, 2,...,n). (7) Notice that (8) Corollary1Let(L, ∨, ∧, 1, 0)be a finite distributive lattice. LetA=(aij)∈Mn(L)be an invertible matrix with each row admitting the same set of entries and 0 occurs at most once in each row or column. Then the length of the largest cycle in the phase spaceG(A) islA=n. In this subsection we consider the linear FDS (Ln,f) such thatfis nilpotent. LetAbe a nilpotent matrix inMn(L).Then there exists a minimal positive integerksuch thatAk=0.We callkthe nilpotent index ofA. Proposition4Let(L, ∨, ∧, 1, 0)be a finite distributive lattice,Aa nilpotent matrix inMn(L) with nilpotent indexk.ThenhA=kandlA=l.The phase spaceG(A) consists of a 1-cycle formed by the zero vector and an in-tree of heightkrooted at the zero vector. ProofBy the definition of the nilpotent indexkwe haveAk+1=0=AkandAk-1≠0=Ak.It follows thathA=kandlA=1. For any vertexx∈Ln,Akx=0∈Ln.This yields that inG(A) there is only one in-tree and the root of tree is the zero vector. Example3Consider the latticeL={0,a,b,c, 1}.The Hasse diagram ofLis depicted in Fig. 5. Fig. 5 Lattice L in Example 3 Fig. 6 Phase space G(A) in Example 3 In this subsection we consider the linear FDS (Ln,f) such thatfis idempotent. LetAbe a idempotent matrix inMn(L) such thatA2=A≠I.Then in the phase spaceG(A),hA=1 andlA=1.The phase spaceG(A) has |ImA| components, or equivalently |ImA| limit cycles, and each element in ImAis a fixed point of (Ln,f). We discuss explicitly the structure ofG(A) for some special idempotent matricesAover a distributive lattice, and general idempotent matrixAover a factor lattice. 2.4.1Idempotentsystemoverafinitedistributivelattice Let (L, ∨, ∧, 1, 0) be a finite distributive lattice. We first consider the phase spaceG(A) such thatAhas only one nonzero column (a,a,...,a)T. Theorem4Let(L, ∨, ∧, 1, 0)be a finite distributive lattice. Assume the matrixA=(aij)∈Mn(L)has only one nonzero column(a,a,...,a)T.LetX={x∈L|x≤a}.Then in the phase spaceG(A), the number of the fixed points is |X|; and the number of preimages of eachy∈ImAisd-(y)=|X|×|L|n-1. ProofA direct computation shows thatA2=A.Assume the nonzero column ofAis thejth column ofA. For eachy∈ImA, there exists a vertexx=(x1,x2,...,xn)Tsuch thaty=Ax=(a∧xj,a∧xj,...a∧xj)T.Thus the vertexy∈ImAis of the form (b,b,...,b)Tsuch thatb=a∧xj. ConsideringA2=Awe havey=Ax=A2x=Ay.It follows thatb=a∧b, or equivalentlyb≤a.Thus we have |ImA|=|{x∈L|x≤a}|. This yields thatd-(y)=|X|×|L|n-1. ProofSinceai∧aj=0(i≠j), a direct computation shows thatA2=A. Conversely, for anyb∈Landy=(b,b,...,b)T, Thus |ImA|=|L|. 2.4.2Idempotentsystemoverafactorlattice Consider a factor lattice (L, ∨, ∧, 1, 0) wherea∨b=lcm(a,b)(the least common multiple ofaandb),a∧b=gcd(a,b)(the greatest common divisor ofaandb). A finite factor lattice is a finite distributive lattice. Lemma8Let (L, ∨, ∧, 1, 0) be a factor lattice. For anyA∈Lassume the solutions toa∧x=0 are 0,x1,x2,...,xs(s≥1).Then forb( ProofFirst we show that eachyi=b∨xiis a solution toa∧y=b(i=1, 2,...,s).This follows from that a∧yi=a∧(b∨xi)=(a∧b)∨(a∧xi)= b∨0=b. Next we assumey0is a solution toa∧y=bandy0≠b.Then we show thaty0=b∨xifor somexi(i∈{1, 2,...,s}).The expressiona∧y0=bmeans thatb=gcd (a,y0).Thus there exists an elementk∈Lsuch thaty0=kb=k∨b, and elementsaandkare mutually prime,i.e.,a∧k=0.The assumptiony0≠bleads to thatk≠0.Therefore,kis a nonzero solution toa∧x=0.Letxi=kTheny0=b∨xi, ending the proof. Notice that ifa∧x=0 has only the trivial solution 0, then the result in the above lemma does not hold. See the following example. Example4Let (L, ∨, ∧, 1, 0) be a factor lattice, and it is presented in Fig. 7. Fig. 7 Factor lattice Consider the equations: 24∧x=1 and 24∧y=12.The first one has a unique solutionx=1,the zero inL.However, the second one has three solutions:y=108, 36 and 12. The following results come directly from Lemma 8. Theorem6Let (L, ∨, ∧, 1, 0) be a factor lattice. Assume the matrixA=(aij)∈Mn(L) has only one nonzero column (a,a,...,a)T.LetX={x∈L|x|a}. For the general nilpotent system, the number of preimages of each vertex in ImAmay not be the same. We give an example as follows. Fig. 8 Lattice L in Example 5 Fig. 9 Phase space G(A) in Example 5 In this paper, we study the phase spaceG(A) of the FDS(Ln,f), wheref(x)=Ax,A∈Mn(L).We give a relationship between the numbers of the limit cycles with different length in Möbius function. We also characterize the phase space for some specific systems such thatfis invertible, nilpotent or idempotent. For an invertible system with an invertible and symmetric matrixAwe present the largest lengthlAof the limit cycles inG(A) and the number of limit cycles of different length. For an invertible FDS (Ln,f)associated with a nonsymmetric matrixAwe give a sufficient condition such that the largest length isn. For a nilpotent system we characterize the structure of the phase space. For some idempotent systems we investigate the number of the fixed points and the number of preimages of each fixed point. An elementxof a setSis called a Garden of Eden ifx≠f(y) for anyy∈S. The Garden of Eden of a dynamical system (S,f) is the set of its Garden of Eden. In the idempotent systems (Ln,f) we consider in Subsection 2.4 each non-fixed point is a Garden of Eden. Then the size of the Garden of Eden is clear for the system (Ln,f) in Theorems 4, 5, 6 and 7.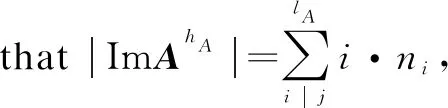

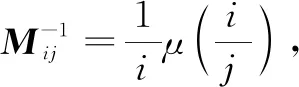
2.2 Invertible system
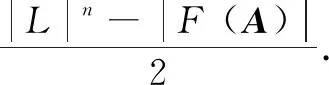
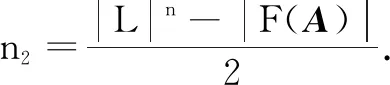

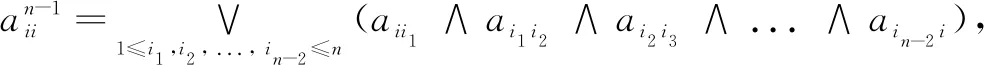
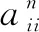
2.3 Nilpotent system


2.4 Idempotent system
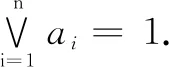
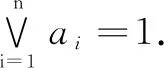
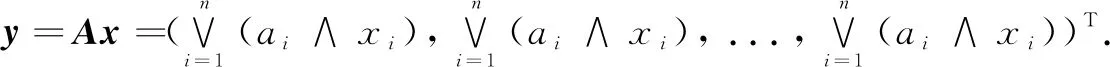

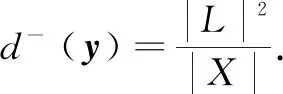



3 Conclusions
 Journal of Donghua University(English Edition)2021年3期
Journal of Donghua University(English Edition)2021年3期
