ARIMA 季节模型在我国艾滋病发病预测中的应用

尤佳豪，张蓓蓓，丁 勇

（南京医科大学康达学院医学信息工程教研室，江苏 连云港 222000）

AIDS 是一种危害性极大的传染病，由感染HIV引起。HIV 是一种能攻击人体免疫系统的病毒，将人体免疫系统中最重要的CD4+T 淋巴细胞作为主要攻击目标，大量破坏该细胞，使人体丧失免疫功能，最后导致死亡。艾滋病主要通过性接触、血液接触、母婴传播等方式进行传播[1]。该病的防治是一项长期的重要任务，良好的预测能对未来近期艾滋病的预防和控制提供预警。国内外用于传染病预测的方法有很多，比较常用的有时间序列分析法[2]、动力学模型[3]、灰色预测等。随着计算机科学的应用和发展，预测理论借助计算机强大的计算能力也得到了较快的发展。预测理论分为3 种，分别是定性预测、定量预测、综合预测。定性预测是通过对当地传染病的流行过程、流行特征及其有关因素的具体分析，判断该病即将流行的趋势和强度。定量预测是借助数学手段利用原始资料，建立恰当的数学模型，预测未来传染病的发病数和发病率。综合预测又称组合预测，是指应用2 种或2 种以上的预测模型对某种传染病进行预测，综合利用各种单个预测模型所提供的信息，以适当的加权平均形式得出组合预测模型。ARIMA 模型适用于各种复杂的时间序列模式，是目前较通用的预测方法之一[4-7]，已广泛应用于传染病发病率的预测，特别是具有季节性趋势的传染病预测。本文收集我国艾滋病发病疫情数据，应用ARIMA 模型拟合全国艾滋病的月发病率，并预测短期艾滋病发病趋势，旨在对这类传染病早期预警提供理论参考。

1 资料与方法

1.1 数据来源 数据资料来源于我国疾病预防控制局 网 站（http://www.nhc.gov.cn/jkj//new_index.shtml）2006 年1 月-2019 年6 月的全国法定报告传染病疫情资料，其中2006 年1 月-2018 年12 月的数据用于建立模型，2019 年1 月-6 月的数据用于验证模型的预测效果。

1.2 方法 建立季节性ARIMA 模型，即ARIMA（p，d，q）（P，D，Q）S，其中p、q 为自回归和移动平均阶数，P、Q 为季节性自回归和移动平均阶数，d、D 为非季节性和季节性差分次数，s 为季节周期。对数据进行数据平稳化处理，通过时序图初步判断序列是否平稳，若为不平稳序列，则针对序列不平稳的趋势性或周期性进行差分或季节性差分处理，实现序列的平稳化。①模型识别：对平稳序列做自相关图，根据自相关函数和偏自相关函数拖尾、截尾情况估计p、d、q 值，建立备选模型；并根据贝叶斯准则（BIC）选择最优模型。②模型检验：选择残差检验的Q 统计量检验，根据各滞后期Q 统计量的P值，检验结果不能拒绝残差不相关的零假设，即模型的残差序列是白噪声序列，所选模型恰当，可用于预测。③预测并验证：运用最终选定的ARIMA 模型进行预测，并与实际值比，计算残差的95%CI（置信区间）以及相对误差，以验证模型的拟合效果。

1.3 统计学方法 采用SPSS 23.0 软件进行数据统计分析，取显著性水平为0.05。

2 结果

2.1 序列的平稳化 2006 年1 月-2018 年12 月我国艾滋病月发病数时间序列图见图1，该序列呈现出明显的非平稳性和季节性（s=12），并随着时间呈现递增。数据经过对数转换、一阶差分和一阶季节差分后达到平稳，见图2。

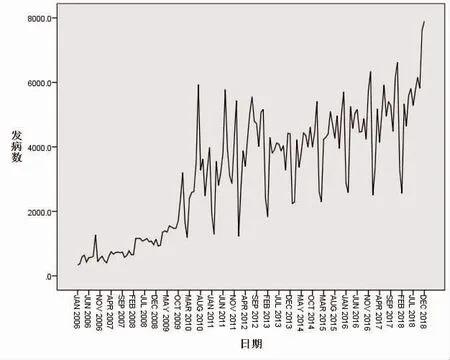
图1 我国艾滋病月发病数时间序列图

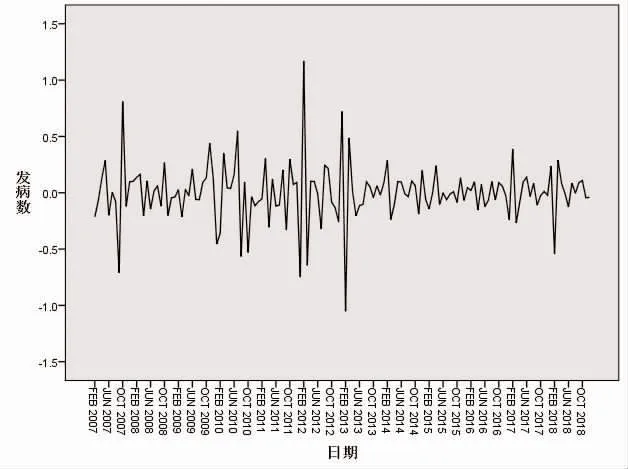
图2 经过转换的数据序列图

2.2 模型的识别与定阶 由于原始数据经过一阶差分和一阶季节差分后达到平稳，取s=12，d=1，D=1；观察差分后的自相关图见图3，ACF 滞后1 阶后趋向0，判断序列的自相关函数呈1 阶截尾，故p=1；观察差分后的偏相关图见图4，PACF 滞后2 阶后逐步趋向0，判断序列的偏相关函数呈2 阶拖尾，故q=2。模型初步为ARIMA（1，1，2）（P，1，Q）12，季节模型的P、Q 值较难判断，但根据文献，参数P、Q 很少超过2 阶，分别取0、1、2（共有9 个模型）由低阶到高阶摸索试验，结合模型的拟合优度、残差以及系数间的相关性进行估计，采用Ljung-Box 方法检验残差白噪声，非白噪声模型排除。

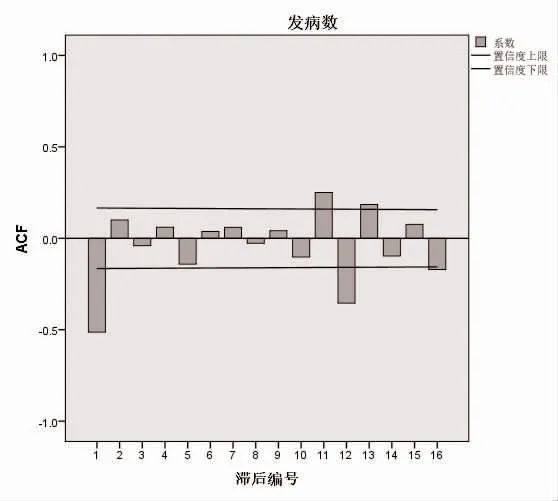
图3 差分后序列的自相关图

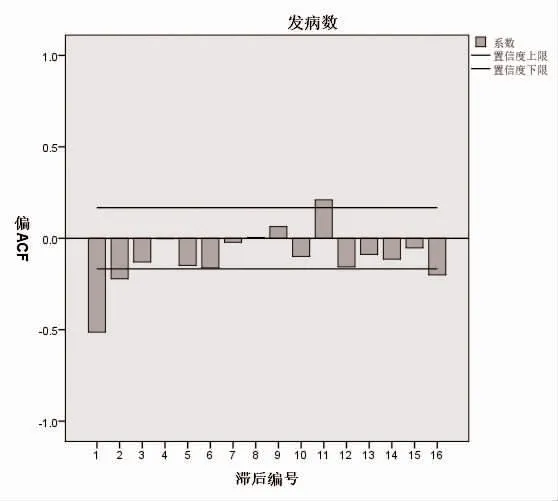
图4 差分后序列的偏相关图

2.3 参数估计及诊断 对9 组模型进行检验，模型ARIMA（1，1，2）（0，1，1）12正态化BIC 值（12.839）最小，R2=0.902 最大，杨-博克斯统计量为18.726，P=0.176，残差序列为白噪声；残差序列的自相关系数及偏相关系数均在95%CI，见图5，由此判断ARIMA（1，1，2）（0，1，1）12模型为最优模型。

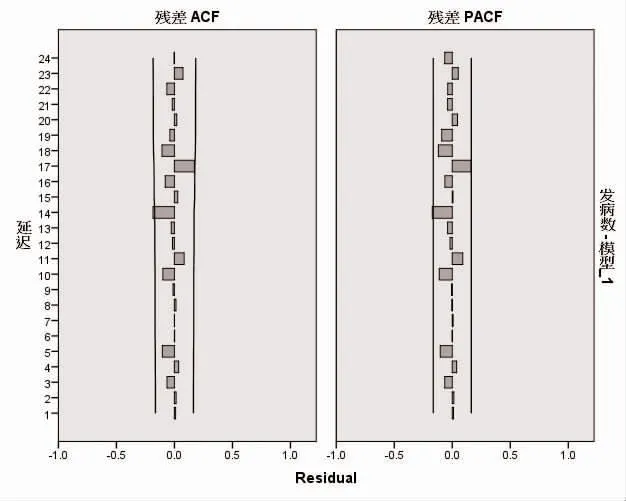
图5 残差序列的自相关系数及偏相关系数

2.4 模型预测 用ARIMA（1，1，2）（0，1，1）12模型预测全国2019 年1 月-6 月艾滋病月发病人数，并对实际数据进行预测精度的验证，见表1，该模型的预测结果平均相对误差率为10.10%，预测值比较接近实际值，该模型具有较好的预测功能。

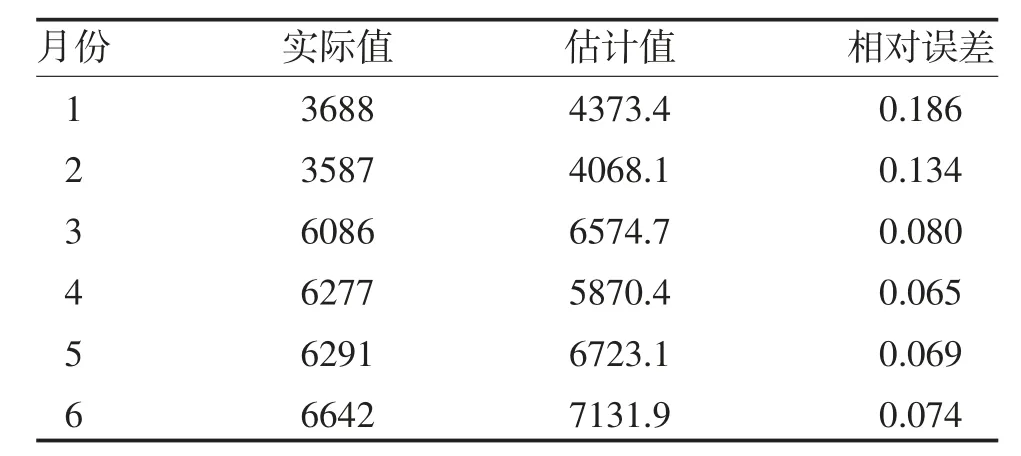
表1 模型预测的误差

3 讨论

在定量预测模型中，ARIMA 模型能将各种已知的、未知的因素综合成统一的影响因素蕴含在时间序列变量中，比较灵活，既适用于非周期性序列，也适用于周期性序列。周期可以为年份、季度、月份，适用范围更广泛且所需的原始资料较少，对短期内传染病的预测效果较佳，具有较为广泛的应用前景。

目前国内对艾滋病的预测研究报告不多，且多是对艾滋病的地区年发病情况进行分析预测，对全国的发病情况进行预测研究的报道较少。本研究结果显示，全国2006 年1 月-2018 年12 月艾滋病发病率呈现出明显季节周期性，且发病率呈逐年上升趋势，有必要对艾滋病发病趋势进行准确预测，提前做好应对措施、制定防控方案。本研究通过正态化BIC 值最小，拟合优度最大，杨-博克斯统计量显著性和残差序列为白噪声等指标，筛选ARIMA（1，1，2）（0，1，1）12模型为拟合效果最优模型；同时利用2019 年上半年艾滋病的月发病率进行预测，结果显示预测的平均误差绝对率为10.10%，预测值接近真实值，提示该模型具有较好的预测功能。

建立ARIMA 模型需要一定数量的历史数据，所建立的模型只能用于短期预测；当获得新数据时，应不断加入新的实际值，以修正或重新拟合更优的模型。因此，在制定艾滋病的预防控制策略和具体的措施时，还必须考虑其他综合因素对预测结果的影响，采用多种方法综合分析[8-10]，会有更好的效果和预测精度。

本文用ARIMA 模型对我国艾滋病发病趋势进行了分析和预测，模型拟合优度为0.902，预测结果的平均相对误差为10.10%，说明ARIMA 模型能够较好地拟合并预测我国艾滋病的月发病人数，为艾滋病的防控提供定量分析的依据。